Проектная работа на тему "Старинные математические задачи" (7 класс). Древние задачи
Новый: Старинные задачиЗадача №1 Продажа сапогов со скидкой.Сапожник сделал сапоги и сказал подмастерью продать их за 25 рублей. К подмастерью на рынке подошло двое инвалидов (у одного нет левой ноги, у другого - правой), и он продал им по сапогу за 12,50 соотвественно. Возвращается, отдает деньги сапожнику и рассказывает, как удачно продал… А сапожник отвечает: “ну что ж ты, инвалидам надо было сделать скидку. Держи 5 рублей, разыщи их и верни по 2,50″ А подмастерье решил отдать инвалидам только по рублю, а остальные три рубля пропил. Нашел инвалидов и отдал каждому по рублю. Вышло, что сапоги обошлись инвалидам по 11,50. 11,50+11,50 = 23 и еще 3 рубля пропиты. Итого: 26 рублей, а было 25. Откуда лишний рубль?Ответ на задачу 1.3 рубля, пропитых подмастерьем, уже входят в 23 рубля, заплаченных инвалидами за сапоги. Поэтому их нельзя складывать, как это сделано в условиях задачи. Сапожник получил за сапоги 25 рублей, затем 5 рублей велел отдать инвалидам. Значит у сапожника осталось 20 рублей. Получается, инвалиды, получив обратно по рублю, заплатили за сапоги 23 рубля, из которых 20 рублей досталось сапожнику, а 3 рубля пропил подмастерье. Никаких “лишних” денег в сделке не возникло. Задача №2 Воз сенаЛошадь съедает воз сена за месяц, коза за два месяца, овца за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?Решение.Поскольку лошадь съедает воз сена за месяц, то за год (12 месяцев) она съест 12 возов сена. Так как коза съедает воз сена за два месяца, то за год она съест 6 возов сена. И наконец, поскольку овца съедает воз сена за 3 месяца, то за год она съест 4 воза сена. Вместе же они съедят за год 12 + 6 + 4 = 22 воза сена. Тогда один воз сена они все вместе съедят за месяца.Задача №3 Основание Карфагена.Об основании города Карфагена существует древнее предание. Дидона, дочь тирского царя, потеряв мужа, убитого ее братом, бежала в Африку. Там она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, а впоследствии был построен и город. Попробуйте приблизительно определить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что размер воловьей шкуры 4 кв. м., а ширина ремешков, на которые Дидона ее разрезала, 1 мм.Ответ:Если площадь воловьей шкуры 4 кв. м. (или 4 млн. кв. мм.), а ширина ремешков 1 мм., то общая длина вырезанного ремня (Дидона, надо думать, вырезала его спирально) - 4 миллиона миллиметров, или 4000 метров, т.е. 4 км. Таким ремнем можно окружить квадратный участок 1 кв. км. и круглый - в 1,3 кв. км. Задача №4 Любители яичницы.Сколько яиц можно съесть натощак?Ответ: Только одно. Все следующие уже будут съедены не на пустой желудок. Задача №5 Влезет или нет?Это старинная головоломка.Вырежьте в листе плотной бумаги круглую дырку и предложите кому-нибудь просунуть в нее монетку, бОльшую по диаметру. Надрывать бумагу или каким-то образом сгибать и ломать, а также распиливать монету - нельзя.Ответ:Сложите лист бумаги "кульком", дыра должна находиться в самом низу. Затем возьмите бумагу обеими руками и попросите кого-нибудь бросить монетку в "кулек" - пусть она упадет прямо на дно и выглянет нижним концом из дырки. После этого слегка приподнимите углы "кулька" - этого окажется достаточно, чтобы отверстие увеличилось и монетка через секунду-другую вывалилась в дырку. При этом бумага осталась неповрежденной. Задача №6. Два отца и два сына.Говорят, что два отца и два сына нашли на дороге, ведущей в Бомбей, три рупии (серебряные монеты) и быстро поделили их между собой, причем каждому досталось по монете. Как им удалось справиться с задачей? Ответ: Путники смогли разделить находку поровну, потому что их было трое: дед, отец и сын (или по-другому - два отца и два сына). Задача №7 Головоломка в стихах.Это русская народная потешка, а в ней интересная загадка.Прилетели галки,Сели на палки.Если на каждой палкеСядет по одной галке,То для одной галкиНе хватит палки.Если же на каждой палкеСядет по две галки,То одна из палокБудет без галок.Сколько было галок?Сколько было палок?Ответ:Четыре галки, три палки .Задача №8 Как выбрать нужного парикмахера?Будучи проездом в маленьком городке, один купец зашел перекусить в ресторанчик, а потом решил постричься. В городке было всего две парикмахерские, и в каждой - только один мастер, он же хозяин. В одной парикмахер был неопрятно побрит и плохо пострижен, а в другой - чисто выбрит и с отличной стрижкой. Купец решил стричься в первой парикмахерской. Как по-вашему, он сделал правильный выбор?Ответ:Купец верно рассудил, что что раз в городе всего два парикмахера, то они наверняка стригут друг друга. Значит, идти стричься надо к тому, у кого плохая стрижка. Задача №9 Бочонок кваса.Один человек выпивает бочонок кваса за 14 дней, а вместе с женой выпивает такой же бочонок кваса за 10 дней. Нужно узнать, за сколько дней жена одна выпивает такой же бочонок кваса . РешениеЗа 140 дней человек выпьет 10 бочонков кваса, а вдвоём с женой за 140 дней они выпьют 4 бочонков кваса. Значит, за 140 дней жена выпьет 14-10=4 бочонка кваса, а тогда один бочонок она выпьет за 140:4=35 дней. Задача №10 Как поделить?Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.Ответ: Один человек берет яблоко вместе с корзиной. Старинные занимательные задачи Здесь вы найдете занимательные задачи из русских учебников математики, опубликованных в России до 1800 года, в частности, из знаменитой "Арифметики" Л.Ф. Магницкого. Это задачи с интересным содержанием или интересными способами решения, задачи, касающиеся интересных свойств чисел, математические игры. Задачи пригодятся на уроках, в математических кружках. Элемент занимательности облегчит обучение, зарядка для ума украсит досуг. НА МЕЛЬНИЦЕ На мельнице имеется три жернова. На первом из них за сутки можно смолоть 60 четвертей зерна, на втором 54 четверти, а на третьем 48 четвертей. Некто хочет смолоть 81 четверть зерна за наименьшее время на этих трех жерновах.За какое наименьшее время можно смолоть зерно и сколько для этого на каждый жернов надо зерна насыпать? ВОЗ СЕНАЛошадь съедает воз сена за месяц, коза - за два месяца, овца - за три месяца.За какое время лошадь, коза и овца вместе съедят такой же воз сена? ДВЕНАДЦАТЬ ЧЕЛОВЕКДвенадцать человек несут 12 хлебов: каждый мужчина несет по 2 хлеба, женщина - по половине хлеба, а ребенок по четверти хлеба.Сколько было мужчин, женщин и детей? КОМУ ПАСТИ ОВЕЦ?У пятерых крестьян - Ивана, Петра, Якова, Михаила Герасима - было 10 овец.Не могли они найти пастуха, чтобы пасти овец.И говорит Иван остальным:"Будем, братцы, пасти овец по очереди - по столько дней сколько каждый из нас имеет овец".По сколько дней должен каждый крестьянин пасти овец, если известно, что у Ивана в два раза меньше овец, чем у Петра, у Якова в два раза меньше, чем у Ивана; Михаил имеет овец в два раза больше, чем Яков, а Герасим - вчетверо меньше, чем Петр? СКОЛЬКО ЯИЦ В ЛУКОШКЕ? Пришел крестьянин на базар и принес лукошко яиц. Торговцы его спросили: "Много ли у тебя в том лукошке яиц?" Крестьянин молвил им так: "Я всего не помню на перечень, сколько в том лукошке яиц. Только помню: перекладывал я те яйца в лукошко по 2 яйца, то одно яйцо лишнее осталось на земле; и я клал в лукошко по 3 яйца, то одно же яйцо осталось; и я клал по 4 яйца, то одно же яйцо осталось; и я их клал по 5 яиц, то одно же яйцо осталось; и я их клал по 6 яиц, то одно же яйцо осталось; и я клал их по 7 яиц, то ни одного не осталось. Сочти мне, сколько в том лукошке яиц было"? КАК УЗНАТЬ ДЕНЬ НЕДЕЛИ?Перенумеровав дни недели, начиная с понедельника, по порядку с 1 до 7, предложите кому-нибудь загадать некоторый день недели. Затем предложите порядковый номер задуманного дня увеличить в 2 раза и к этому произведению прибавить 5. Полученную сумму предложите умножить на 5, а затем то, что получится, умножить на 10. По объявленному результату вы называете день недели, который был загадан. Как узнать загаданный день недели? СКОЛЬКО РАЗ СОВМЕСТЯТСЯ СТРЕЛКИ?Часы пробили полночь. Сколько раз и в какие моменты времени до следующей полуночи часовая и минутная стрелки будут совмещаться? ОБМЕН ЗАЙЦЕВ НА КУРКрестьянин менял зайцев на кур: брал за всяких двух зайцев по три курицы.Каждая курица снесла яйца - третью часть от числа всех куриц.Крестьянин, продавая яйца брал за каждые 9 яиц по столько копеек, сколько каждая курица снесла яиц, и выручил 72 копейки.Сколько было кур и сколько зайцев? ЗА СКОЛЬКО МИНУТ? Ребята пилят бревна на метровые куски. Отпиливание одного такого куска занимает одну минуту.За сколько минут они распилят бревно длиной 5 метров? КОЗА Один человек купил трех коз и заплатил 3 рубля. Спрашивается: по чему каждая коза пошла? МНОГО ЛИ НОГ?Мельник пришел на мельницу. В каждом из четырех углов он увидел по 3 мешка, на каждом мешке сидело по 3 кошки, а каждая кошка имела при себе троих котят.Спрашивается, много ли ног было на мельнице? ЧТО ЭТО ТАКОЕ?Что это такое две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три, бросили их в четыре, чтобы четыре оставили одну? ПОЛТАБУНА И ПОЛ-ЛОШАДИ К табунщику пришли три казака покупать лошадей."Хорошо, я вам продам лошадей, - сказал табунщик, - первому продам я полтабуна и еще половину лошади, второму - половину оставшихся лошадей и еще пол-лошади, третий также получит половину оставшихся лошадей с полулошадью.Себе же оставлю только 5 лошадей".Удивились казаки, как это табунщик будет делить лошадей на части. Но после некоторых размышлений они успокоились, и сделка состоялась.Сколько же лошадей продал табунщик каждому из казаков? ВОЗМОЖНО ЛИ ТАКОЕ?Что это может быть: две головы, две руки и шесть ног, а в ходьбе только четыре? ДВА ОТЦА И ДВА СЫНАДва отца и два сына поймали трех зайцев, а досталось каждому по одному зайцу. Спрашивается, как это могло случиться? КАК ЭТО МОГЛО БЫТЬ?У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25.Как это могло быть? НАПИСАТЬ ЧИСЛОНаписать цифрами число, состоящее из одиннадцати тысяч, одиннадцати сотен и одиннадцати единиц. РЫЦАРИ И ОРУЖЕНОСЦЫ Три рыцаря, каждый в сопровождении оруженосца, съехались на берегу реки и хотят переправиться на другой берег.Есть лодка, которая может вместить только двух человек.Могут ли переправиться рыцари и их оруженосцы на другой берег при условии, что оказавшись отдельно от своего рыцаря, ни один оруженосец не находился бы при этом в обществе других рыцарей? ИЗ ПАПИРУСА АХМЕСА (Египет, около 2000 лет до н.э.). ПАСТУХ Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты из своего многочисленного стада? Пастух отвечает: - Я привожу две трети от трети скота. Сочти, сколько быков в стаде? ИЗ КНИГИ «ТЫСЯЧА И ОДНА НОЧЬ» Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся. Так же она поступила и с третьим стражником, а когда она поделилась яблоками с четвёртым стражником, у неё осталось 10 яблок. Сколько яблок она собрала в саду? ИНДИЯ Брахмагупта, около 600 г. Слон, слониха и слонёнок пришли напиться к озеру, чтобы напиться воды. Слон может выпить озеро за 3ч, слониха - за 5ч, а слонёнок - за 6ч. За сколько времени они все вместе выпьют озеро? ИЗ АКМИМСКОГО ПАПИРУСА (VI в.) Некто взял из сокровищницы 1/13. Из того, что осталось, другой взял 1/17. Оставил же в сокровищнице 192. Мы хотим узнать, сколько было в сокровищнице первоначально? ИЗ КНИГИ «КОСС» Адама Ризе (XVI в.) Трое выиграли некоторую сумму денег. На дою первого пришлось ¼ этой суммы, на долю второго -1/7, а долю третьего – 17 флоринов. Как велик весь выигрыш? ОСНОВАНИЕ КАРФАГЕНА Об основании города Карфагена существует древнее предание. Дидона, дочь тирского царя, потеряв мужа, убитого ее братом, бежала в Африку. Там она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, а впоследствии был построен и город. Попробуйте приблизительно определить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что размер воловьей шкуры 4 кв. м., а ширина ремешков, на которые Дидона ее разрезала, 1 мм . МУДРОСТЬ МАНДАРИНА То, что здесь будет рассказано, произошло в Китае. Один из провинциальных китайских мандаринов, благодаря своему необыкновенному уму и способностям, а также и той популярности, которой он пользовался среди народа, возбудил сильную зависть к себе других знатных китайцев. Зависть скоро перешла в злейшую ненависть - интригам и козням не было конца. В результате, как это часто бывает, умный и добрый мандарин сначала впал в немилость императора, а потом, благодаря проискам врагов, был отдан под суд, причём судьями, конечно, оказались злейшие враги мандарина, которые в то время ничего не желали так сильно, как только его скорейшей смерти. Само собой разумеется, вынести смертный приговор ничего не стоило, но ... объявить его публично, в присутствии того народа, который так искренне был привязан к своему правителю - на это они не могли решиться. А потому они заранее решили между собой, что на заседании, в день, назначенный для суда над мандарином, они объявят приговор приблизительно в такой форме: "Так как мы, товарищи подсудимого, не желаем брать на свою совесть ответственность перед великим Буддой за жизнь подсудимого, и так как, всё-таки, обвинения, предъявленные ему, остаются неопровергнутыми, а отчасти и доказанными, то мы, судьи, назначенные сюда по повелению самого императора, постановили предоставить самой судьбе решить участь подсудимого. В каждую из этих двух урн мы кладём по свёрнутой записке, на одной из которых написано слово "жизнь", а на другой - "смерть", и предоставляем подсудимому право самому вынуть любую из этих записок и тем самым назначить себе приговор". Такова должна была быть внешняя сторона дела. На самом же деле коварные судьи решили на обеих записках написать слово "смерть" и, таким образом, участь несчастного мандарина была предрешена заранее. По счастливой случайности адвокату, который был назначен защищать на суде мандарина, удалось узнать о коварном плане судей. Конечно, самое лучшее, что он мог бы теперь сделать - это вывести судей на чистую воду, уличив их во время суда в подлоге. Но ... для адвоката это было бы равносильно самоубийству, а потому он ограничился только тем, что накануне дня суда сообщил подсудимому о том, что ему удалось узнать. Казалось бы, обстоятельства сложились как нельзя плохо, и придумать что-нибудь для того, чтобы предотвратить неминуемую гибель подсудимого, было невозможно... Но, как уже было сказано, мандарин был очень умным человеком. Проведя всю ночь перед судом в размышлении и взвесив все обстоятельства, он нашёл, наконец, верное средство для того, чтобы спасти свою жизнь, даже не уличая судей в их замысле и не показывая виду, что он раскрыл их план. Настал день суда. Публики было видимо-невидимо. Ещё бы! Судят ведь того, кто так много сделал для народа! Судьи объявили приговор в той форме, которая была приведена выше, опустили в каждую из двух урн по заранее приготовленной записке и с нетерпением ожидали известного им заранее приговора. Подсудимый уверенно подошёл к судейскому столу, сунул без всякого колебания руку в одну из урн, вытащил оттуда свёрнутую записку и ... Как вы думаете, что же он сделал? Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и дикий гусь вылетают одновременно. Через сколько дней они встретятся? Древнеримская задача (IIв.) Некто, умирая, завещал: « Если у моей жены родится сын, то пусть ему будет 2/3 имения, а жене – остальная часть. Если же родится дочь, то ей 1/3, а жене 2/3». Родилась двойня – сын и дочь. Как же разделить имение? НАЕМ Хозяин, принимая работника, предложил ему следующее испытание: - Вот тебе бочка, наполни её ровно наполовину, ни больше, ни меньше. Но смотри, ни палкой, верёвкой или чем-либо другим для измерения не пользуйся. Работник справился с заданием. Как он это сделал? Анания Ширакаци (615 г.) - армянский философ, математик и географ середины 7 века. В городе Афины был водоем, в который проведены три трубы. Одна из труб может наполнить водоем за 1 ч, другая, более тонкая, - за 2 ч, третья, еще более тонкая, - за 3 ч. За какую часть часа все три трубы вместе наполнят водоем? Задача С. Сатина из журнала «Крокодил» (1990. № 34): За десять дней пират Ерема Способен выпить бочку рома. А у пирата у Емели Ушло б на это две недели. За сколько дней прикончат ром Пираты, действуя вдвоем? СТАРИННЫЕ РУССКИЕ ЗАДАЧИ Здесь вы найдете занимательные задачи из русских учебников математики, опубликованных в России до 1800 года, в частности, из знаменитой "Арифметики" Л.Ф. Магницкого. Это задачи с интересным содержанием или интересными способами решения, задачи, касающиеся интересных свойств чисел, математические игры. Задачи пригодятся на уроках, в математических кружках. Элемент занимательности облегчит обучение, зарядка для ума украсит досуг. НА МЕЛЬНИЦЕ На мельнице имеется три жернова. На первом из них за сутки можно смолоть 60 четвертей зерна, на втором 54 четверти, а на третьем 48 четвертей. Некто хочет смолоть 81 четверть зерна за наименьшее время на этих трех жерновах. За какое наименьшее время можно смолоть зерно и сколько для этого на каждый жернов надо зерна насыпать? ДВА КРЕСТЬЯНИНА Работали два крестьянина в поле и решили пообедать. У первого было два хлеба, а у второго - один. В это время подошёл к ним третий и попросил поделиться. Ему дали один хлеб и каждый съел по хлебу. За свою долю крестьянин дал им 6 рублей и, поблагодарив, ушёл. Как поделить оставшимся эти деньги? КОМУ ПАСТИ ОВЕЦ? У пятерых крестьян - Ивана, Петра, Якова, Михаила Герасима - было 10 овец. Не могли они найти пастуха, чтобы пасти овец. И говорит Иван остальным: "Будем, братцы, пасти овец по очереди - по столько дней сколько каждый из нас имеет овец". По сколько дней должен каждый крестьянин пасти овец, если известно, что у Ивана в два раза меньше овец, чем у Петра, у Якова в два раза меньше, чем у Ивана; Михаил имеет овец в два раза больше, чем Яков, а Герасим - вчетверо меньше, чем Петр? СКОЛЬКО ЯИЦ В ЛУКОШКЕ? Пришел крестьянин на базар и принес лукошко яиц. Торговцы его спросили: "Много ли у тебя в том лукошке яиц?" Крестьянин молвил им так: "Я всего не помню на перечень, сколько в том лукошке яиц. Только помню: перекладывал я те яйца в лукошко по 2 яйца, то одно яйцо лишнее осталось на земле; и я клал в лукошко по 3 яйца, то одно же яйцо осталось; и я клал по 4 яйца, то одно же яйцо осталось; и я их клал по 5 яиц, то одно же яйцо осталось; и я их клал по 6 яиц, то одно же яйцо осталось; и я клал их по 7 яиц, то ни одного не осталось. Сочти мне, сколько в том лукошке яиц было"? КАК УЗНАТЬ ДЕНЬ НЕДЕЛИ? Перенумеровав дни недели, начиная с понедельника, по порядку с 1 до 7, предложите кому-нибудь загадать некоторый день недели. Затем предложите порядковый номер задуманного дня увеличить в 2 раза и к этому произведению прибавить 5. Полученную сумму предложите умножить на 5, а затем то, что получится, умножить на 10. По объявленному результату вы называете день недели, который был загадан. Как узнать загаданный день недели? СКОЛЬКО РАЗ СОВМЕСТЯТСЯ СТРЕЛКИ? Часы пробили полночь. Сколько раз и в какие моменты времени до следующей полуночи часовая и минутная стрелки будут совмещаться? ОБМЕН ЗАЙЦЕВ НА КУР Крестьянин менял зайцев на кур: брал за всяких двух зайцев по три курицы. Каждая курица снесла яйца - третью часть от числа всех куриц. Крестьянин, продавая яйца брал за каждые 9 яиц по столько копеек, сколько каждая курица снесла яиц, и выручил 72 копейки. Сколько было кур и сколько зайцев? ЗА СКОЛЬКО МИНУТ? Ребята пилят бревна на метровые куски. Отпиливание одного такого куска занимает одну минуту. За сколько минут они распилят бревно длиной 5 метров? КОЗА Один человек купил трех коз и заплатил 3 рубля. Спрашивается: по чему каждая коза пошла? МНОГО ЛИ НОГ? Мельник пришел на мельницу. В каждом из четырех углов он увидел по 3 мешка, на каждом мешке сидело по 3 кошки, а каждая кошка имела при себе троих котят. Спрашивается, много ли ног было на мельнице? ЧТО ЭТО ТАКОЕ? Что это такое две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три, бросили их в четыре, чтобы четыре оставили одну? ПОЛТАБУНА И ПОЛ-ЛОШАДИ К табунщику пришли три казака покупать лошадей. "Хорошо, я вам продам лошадей, - сказал табунщик, - первому продам я полтабуна и еще половину лошади, второму - половину оставшихся лошадей и еще пол-лошади, третий также получит половину оставшихся лошадей с полулошадью.Себе же оставлю только 5 лошадей". Удивились казаки, как это табунщик будет делить лошадей на части. Но после некоторых размышлений они успокоились, и сделка состоялась. Сколько же лошадей продал табунщик каждому из казаков? ВОЗМОЖНО ЛИ ТАКОЕ? Что это может быть: две головы, две руки и шесть ног, а в ходьбе только четыре? ДВА ОТЦА И ДВА СЫНА Два отца и два сына поймали трех зайцев, а досталось каждому по одному зайцу. Спрашивается, как это могло случиться? КАК ЭТО МОГЛО БЫТЬ? У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть? НАПИСАТЬ ЧИСЛО Написать цифрами число, состоящее из одиннадцати тысяч, одиннадцати сотен и одиннадцати единиц. РЫЦАРИ И ОРУЖЕНОСЦЫ Три рыцаря, каждый в сопровождении оруженосца, съехались на берегу реки и хотят переправиться на другой берег. Есть лодка, которая может вместить только двух человек. Могут ли переправиться рыцари и их оруженосцы на другой берег при условии, что оказавшись отдельно от своего рыцаря, ни один оруженосец не находился бы при этом в обществе других рыцарей? ПУТНИК Путник, догнав другого, спросил его: «Далеко ли до деревни, которая впереди?» Другой путник ответил: « Расстояние от деревни, из которой ты идёшь, равно трети всего расстояния меду деревнями. А если пройдёшь ещё две версты, будешь ровно посередине между деревнями. Сколько вёрст осталось идти первому путнику? ПЛОТНИКИ Четыре плотника хотят построить дом. 1 плотник может построить дом за год, второй - за 2 года, третий - за три года, четвёртый - за 4 года. За сколько лет они построят дом при совместной работе? ВОЗ СЕНА Лошадь съедает воз сено за месяц, коза - за два месяца, овца - за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена? РУССКАЯ НАРОДНАЯ ПОТЕШКА Прилетели галки, Сели на палки. Если на каждой палке Сядет по одной галке, То для одной галки Не хватит палки. Если же на каждой палке Сядет по две галки, То одна из палок Будет без галок. Сколько было галок? Сколько было палок? Словарь единиц измерения Верста (поприще) – мера длины, равная 1,06 км Аршин – мера длины, равная 0,71 м Алтын – денежная единица, равная 3 копейкам Полушка – денежная единица, равная 0,25 рублей Гривна – денежная единица, равная 10 копейкам Фунт – мера веса, равная 453,6 г Сажень – мера длины, равная 2,13 м Четверть – мера, равная четвертой части какой-либо единицы измерения Пядь – расстояние между вытянутыми большим и указательным пальцами руки при их наибольшем удалении. (19 – 23 см) Локоть – расстояние от конца вытянутого среднего пальца руки до локтевого сгиба. (38 – 46 см) Вершок – мера длины, равная 4,5 см Задача Л. Ф. Магницкого (из «Арифметики») Некий торговец купил 112 баранов старых и молодых, дал 49 рублёв 20 алтын, за старого платил по 15 алтын и по 2 деньги, а за молодого по 10 алтын, и ведательно есть, колико старых и молодых баранов купил он. Задача Л. Ф. Магницкого (из «Арифметики»). Спросил некто учителя скажи, сколько у тебя в классе учеников, так как хочу отдать к тебе в учение своего сына. Учитель ответил если придет еще учеников столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда будет у меня учеников 100. Спрашивается, сколько было у учителя учеников? Задача о гусях. Летело стадо гусей, навстречу им летит один гусь и говорит «Здравствуйте, сто гусей», а те ему отвечают «Нет, нас не сто гусей, а если бы нас было еще столько, сколько есть, да еще полстолько, да четверть столько, да еще ты, один гусь с нами, тогда нас было бы ровно сто гусей». Сколько их было? Задача Гольдбаха. Всякое нечетное число, большее пяти, может быть представлено в виде суммы трех простых чисел. Проверьте это на примере нескольких двузначных чисел. Задача Эйлера. Каждое четное число, начиная с четырех, можно разбить на сумму двух простых чисел. Проверьте это на примере нескольких двузначных чисел . Задача Эйлера (из учебника «Введение в алгебру»). Две крестьянки принесли на рынок 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала второй «Будь у меня твои яйца, я выручила бы 15 крейцеров». Вторая ответила «А будь твои яйца у меня, я выручила бы за них 6 I крейцера». Сколько яиц было у каждой? Задача Л. Н. Толстого. В рассказе Л. Н. Толстого «Много ли человеку земли нужно» крестьянину отводилось столько земли, сколько он успевал обежать в течение одного дня. По какому контуру ему выгоднее было бежать по квадратному, шестиугольному [правильный шестиугольник] или по кругу Указание: при равенстве периметров этих фигур какая имеет большую площадь? Задача Л. Н. Толстого. Артели косцов надо было скосить два луга, один вдвое больше другого. Поло- вину дня артель косила большой луг. После этого артель разделилась пополам первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели? Задача Л. Н. Толстого. На противоположных стенах комнаты определенной длины и ширины сидят муха и паук, муха — на полтора аршина от пола, паук — на полтора аршина от потолка. Какое между ними кратчайшее расстояние, которое мог бы проползти паук, чтобы достать муху? Задача Льва Толстого Продавец продает шапку. Стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только 25 р. Продавец отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает и отдает 10+10+5. Продавец отдает шапку и сдачу в 15 руб. Через какое то время приходит соседка и говорит, что 25 р. фальшивые, требует отдать ей деньги. Ну что делать. Продавец лезет в кассу и возвращает ей деньги. На сколько обманули продавца? Задача Л. Ф. Магницкого (из «Арифметики»). Послан человек из Москвы на Вологду, и велено ему в хождении своем совершати на всякий день по 40 верст; потом другий человек в другий [на следующий] день послан в след его, и велено ему идти на день 45 верст, и ведательно есть, в коликий день постигнет [догонит]второй первого Двенадцать человек Двенадцать человек несут 12 хлебов: каждый мужчина несет по 2 хлеба, женщина — по половине хлеба, а ребенок по четверти хлеба. Сколько было мужчин, женщин и детей? На мельнице На мельнице имеется три жернова. На первом из них за сутки можно смолоть 60 четвертей зерна, на втором 54 четверти, а на третьем 48 четвертей. Некто хочет смолоть 81 четверть зерна за наименьшее время на этих трех жерновах. За какое наименьшее время можно смолоть зерно и сколько для этого на каждый жернов надо зерна насыпать? Собака и заяц Собака усмотрела зайца в 150 саженях от себя. Заяц пробегает за 2 минуты 500 саженей, а собака — за 5 минут 1300 саженей. За какое время собака догонит зайца? На охоте Пошел охотник на охоту с собакой. Идут они лесом, и вдруг собака увидала зайца. За сколько скачков собака догонит зайца, если расстояние от собаки до зайца равно 40 скачкам собаки и расстояние, которое пробегает собака за 5 скачков, заяц пробегает за 6 скачков? (В задаче подразумевается, что скачки делаются одновременно и зайцем и собакой.) В жаркий день В жаркий день 6 косцов выпили бочонок кваса за 8 часов. Нужно узнать, сколько косцов за 3 часа выпьют такой те бочонок кваса. Бочонок Один человек выпивает бочонок кваса за 14 дней, а вместе с женой выпивает такой же бочонок кваса за 10 дней. Нужно узнать, за сколько дней жена одна выпивает такой же бочонок кваса. Паромщик Паромщик многие годы зарабатывал на жизнь тем, что перевозил через реку людей, их скраб и животных. Платы он большой не взимал, поэтому люди охотно пользовались его услугами, но за всю жизнь так и не удалось ему скопить денег на новый большой паром. На его маленьком пароме хватало места только для самого паромщика и еще чего-нибудь одного. Однажды ему нужно было переправить через реку волка, козу и капусту. Но вот неудача - волка с козой без присмотра оставлять нельзя, козу с капустой тоже.Объясните паромщику как в целости и сохранности переправить через реку капусту и животных? Задача Л.Н. Толстого Пять братьев разделили после отца наследство поровну. В наследстве было три дома. Три дома нельзя было делить, их взяли старшие три брата. А меньшим за то выделили деньги. Каждый из старших заплатил по 800 руб меньшим. Меньшие разделили эти деньги между собой, и тогда у всех братьев стало поровну. Много ли стоили дома?(ответ по 2000руб) Из рассказа А.П. Чехова "Репетитор" Купец купил 138 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб за аршин, а черное 3 руб за аршин(ответ:63 и 75) Из "Всеобщей арифметики" И. Ньютона Некто желает распределить между бедными деньги. Если бы у него было на восемь динаров больше, то он мог бы дать каждому по три, но он раздал лишь по два, и у него еще остается три. Сколько бедных?( ответ: 11) Два почтальона А и В находятся друг от друга на расстоянии 59 мил. Утром они отправляются друг другу навстречу. А приходит в 2ч 7 миль. В в 3 ч 8миль, но В выходит, часом позднее, чем А. Сколько миль пройдет А до встречи с В?(ответ 35миль) Из "Арифметики" Магницкого Некий человек купил ладану 137 пудов. За каждый пуд заплатил по 6 рублей и захотел узнать, сколько стоит покупка? Некто купил зерна 2359 четвертей, за четверть платил по 65 коп. и отдал всех денег 153335 коп. Проверьте вычисления Некто оставил в наследство жене, дочери и трем сыновьям 48000 рублей и завещал жене 1/8 всей суммы, а каждому из сыновей вдвое больше, чем дочери. Сколько досталось каждому из наследников? (ответ жене и дочери по6000, сыновьям по12000) Купил полторажды полтора аршина, дал полтретьяжды полтретьи гривны. Сколько надо дать за полдевятажды полдевята аршина? В саринных русских руководствах по арифметике использовались такие названия дробей ½ -половина, ¼-четь, 1/8-полчеть, 1/16- полполчеть, 1/32-полполполчеть, 1 ½-полтора, 2 ½ полтрети, 3 ½ полчетверта, 4 1/2полпята(ответ 200 25/36) Древнекитайская задача В клетке сидят фазаны и кролики. У них вместе 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?(ответ:12,23) novijmir.blogspot.com Задачи Древней Греции (5-й, 6-й классы)  Разделы: Математика, История и обществознание, Социальная педагогика
Урок – путешествие о Древней Греции на тему:
Задачи Древней Греции.
Доска бела от мела.
Рука устала, затекла спина,
Мы друг на друга смотрим очумело,
А все-таки задача решена!
Додумались! Добились! "Раскололи"!
Намаялись, однако же смогли!
Забыли о кино и о футболе,
Звонку не рады – до чего дошли.
Мы хотим, чтобы вы полюбили математику.
(Звучит мелодия "Сиртаки").
- Звуки музыки переносят нас в Древнюю Грецию,
VIIв. до н.э.
(Группа девочек в национальных костюмах
исполняет танец).
Древние греки были удивительно талантливым
народом, у которого есть чему поучиться даже
сейчас. В те времена Греция состояла из многих
мелких государств. Каждый раз, когда приходилось
решать какой-нибудь важный государственный
вопрос, горожане собирались на площади,
обсуждали его, спорили, а потом голосовали. Они
были хорошими "спорщиками". По преданию, в то
время сложилось утверждение: " В споре
рождается истина!" Греки отличались
трудолюбием и смелостью. Среди них были отличные
строители, мореплаватели, купцы и художники. Они
внесли большой вклад в развитие культуры и науки,
особенно математики.
Так кто же они, знаменитые древнегреческие
ученные?
- Пифагор Самосский – великий греческий ученный,
человек – символ, философ и пророк. Он
организовал школу, которую назвали
пифагорейской.
А теперь решим задачу о школе Пифагора:
Задача о школе Пифагора
Первое построение геометрии как
дедуктивной науки принадлежит Пифагору
Самосскому (ок.570 – ок.500 до н.э.) –
древнегреческому математику и философу. В
молодости Пифагор путешествовал по Египту и
Вавилону, изучая мудрость жрецов. Около 530г. до
н.э. он переехал в Кротон (Южная Италия), где
основал знаменитый пифагорейский союз (школу).
Деятельность союза была окружена тайной. В школе
Пифагора процветала числовая мистика. Пифагор
учил, что "число есть сущность всех вещей".
Пифагорейцы занимались астрономией, геометрией,
гармонией (теорией музыки) и арифметикой (теорией
чисел). В их школе возникло представление о
шарообразности Земли.
Ученик читает текст задачи (в образе
Пифагора).
Тиран острова Самос Поликрат однажды спросил
у Пифагора, сколько у того учеников. "Охотно
скажу тебе, о Поликрат, - отвечал Пифагор. –
половина моих учеников изучает прекрасную
математику, четверть исследует тайны вечной
природы, седьмая часть молча упражняет силу духа,
храня в сердце учение. Добавь к ним трех юношей,
из которых Теон превосходит прочих своими
способностями. Столько учеников веду я к
рождению вечной истины". Сколько учеников было
у Пифагора?
Решение (метод подбора):
НОК (2,4,7) = 2*4*7=28
Ответ: 28 учеников.
- Почти все математики древности занимались
уравнениями. Много внимания им уделял
древнегреческий ученный Диофант.
Почти все математики древности занимались
уравнениями. Много внимания им уделял, а главное,
много нового внес в способы их решения
древнегреческий ученый Диофант.
О Диофанте известно очень мало. Есть основание
полагать, что он жил около III в. н.э. Одна группа
уравнений, так называемые неопределенные
уравнения, до сих пор называются диофантовыми
уравнениями. Именно для них он нашел способ
решения.
Скудные сведения о Диофанте может дополнить
нам лишь надпись на надгробном камне,
сформулированная задача в стихах:
Здесь погребен Диофант, в камень могильный
При счете искусном расскажет нам,
Сколь долог был его век.
Велением бога он мальчиком был шестую часть
своей жизни,
В двенадцатой части прошла его юность.
Седьмую часть жизни прибавим – пред нами очаг
Гименея,
Пять лет протекло и прислал Гименей ему сына
Но горе ребенку! Едва половину он прожил
Тех лет, что отец, скончался несчастный.
Четыре года страдал Диофант от утраты той тяжкой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть восприял Диофант?
Решение:
НОК (6,12,7,2) = 12*7 = 84
Ответ: 84 года.
- Сценка: Зенон – древнегреческий философ.
Однажды ученики греческого философа Зенона
обратились к нему с вопросом: "Учитель! Ты,
обладающий знаниями во много раз большими, чем
мы, всегда сомневаешься в правильности ответов
на вопросы, которые нам кажутся очевидными,
ясными. Почему?" Начертив посохом на песке два
круга, большой и малый, старец молвил: "площадь
большего круга – это познанное мною, а площадь
малого круга – это познанное вами. Как видите,
знаний у меня действительно больше, чем у вас. Но
все, что вне кругов – это не познанное ни мной, ни
вами. Согласитесь, что длина большой окружности
больше длины малой, а следовательно, и граница
моих знаний с непознанным большая, чем у вас. Вот
почему у меня больше сомнений."
А сколько еще интересных греческих ученых вы
еще встретите на уроках. Вот их имен: Платон,
Евклид, Архимед, Гипсикл, Герон, Эратосфен,
Гипатия.
Гипатия – дочь известного греческого
математика Теона. Она родилась и жила в
Александрии с 370 по 415 года. Гипатия была первой
женщиной математиком, философом, астрономом и
врачом. Она была настолько всесторонне
образованна, что с ее мнением считались все
ученные ее времени. После смерти Гипатии в
течении более тысячи лет мы не встречаем женщин
– математиков.
4. Задача о кресте
Древние греки на хлебах чертили крест,
считая его символом жизни.
А теперь задача: разрежьте крест на четыре
части и сложите из получившихся частей квадрат.
Греческая антология – арифметический сборник,
содержащий 48 задач, условия, которых написаны в
стихотворной форме.
5. Задача "Суд Париса"
Один из древнейших мифов содержит сказание о
суде троянского царевича Париса…
Однажды на свадьбе богиня раздора Эрида
подбросила собравшимся гостям яблоко с надписью
"прекраснейшей". Из-за этого яблока возник
спор между богиней мудрости и справедливой войны
Афиной, богиней любви и красоты Афродитой и
сестрой и супругой Зевса Герой. Они обратились к
царю и отцу богов и людей Зевсу, чтобы он решил,
кому должно достаться яблоко. Зевс оправил
богинь на гору к Парису, который пас там свои
стада. Парис должен был решить, какая из богинь
самая прекрасная. Каждая из богинь пыталась
склонить юношу на свою сторону: Афина предлагала
мудрость и военную славу, Афродита – красивейшую
женщину на земле в жены, Гера – власть и
богатство.
Как Парис определил прекраснейшую из богинь,
можно узнать, решив старинную задачу.
Задача:
Богини Гера, Афродита и Афина пришли к юному
Парису, чтобы тот решил, кто из них прекраснее.
Представ перед Парисом, богини высказали
следжующие утверждения.
Афродита. Я самая прекрасная. (1)
Афина. Афродита не самая прекрасная. (2)
Гера. Я самая прекрасная. (3)
Афродита. Гера не самая прекрасная. (4)
Афина. Я самая прекрасная. (5)
Парис, прилегший отдохнуть на обочине дороги,
не счел нужным даже снять платок, которым прикрыл
глаза от яркого солнца. Но богини были
настойчивы, и ему нужно было решить, кто из них
самая прекрасная. Парис предположил, что все
утверждения прекраснейшей из богинь истины, а
все утверждения двух остальных богинь ложны. Мог
ли Парис вынести решение, кто прекраснее из
богинь?
Ответ: Афродита – прекраснейшая из богинь.
6. Задача о музах:
По представлению древних греков науками и
искусствами ведали мифические женские существа
– музы:
Евтерна – богиня-покровительница музыки;
Клио – истории;
Талия – комедии;
Мельпомена – трагедии;
Терпсихора – танцев и хорового пения;
Эрато – поэзии;
Полимния – лирической поэзии;
Урания – астрономии;
Каллиопа – эпоса и красноречия.
Местопребыванием муз и Аполлона служила гора
Геликон. Учреждения, где протекала деятельность
ученых, назывались музеумами (музеями) –
жилищами муз. В поэтической задаче о музах бог
любви Эрот жалуется богине красоты и любви
Киприде на муз.
Видя, что плачет Эрот, Киприда его вопрошает:
“Что так тебя огорчило, ответствуй немедля!” “Яблок
я нес с Геликона немало” – Эрот отвечает – Музы,
отколь ни возьмись, напали на сладкую ношу.
Частью двенадцатой вмиг овладела Евтерпа, а Клио
пятую долю взяла. Талия – долю восьмую. С частью
двадцатой ушла Мельпомена. Четверть взяла
Терпсихора. С частью седьмою Эрато от меня
убежала. Тридцать плодов утащила Полимния. Сотня
и двадцать взяты Уранией; триста плодов унесла
Каллиопа. Я возвращаюсь домой почти что с пустыми
руками. Только полсотни плодов оставили мне музы
на долю.
Сколько яблок нес Эрот до встречи с музами?
Решение:
НОК (12,5,8,20,4,7) = 7*8*20*3 = 3360
Ответ: 3360 яблок.
7. Задача о статуе Минервы
Сохранилась “Греческая антология” в форме
сборника задач, составленных в стихах, главным
образом гекзаметром, которым, как известно,
написаны знаменитые поэмы Гомера (IX-VIII вв. до н.э.)
“Илиада” и “Одиссея”. “Греческая антология”
была написана в VI в. н.э. грамматиком Метродором. В
“Греческой антологии” содержится задача о
статуе богини мудрости, покровительнице наук,
искусств и ремёсел Минерве.
Я – изваянье из злата. Поэты то злато
В дар принесли: Харизий принёс половину всей
жертвы,
Феспия часть восьмую дала; десятую Солон.
Часть двадцатая – жертва певца Фемисона, а
девять
Всё завершивших талантов – обет, Аристоником
данный.
Сколько же злата поэты все вместе в дар принесли?
Решение. НОК (2,8,10,20) = НОК (8,20) = 40
Ответ: 40
8. Лабиринты
Лабиринты – слово греческое, означает “ходы в
подземельях”. Безвыходных лабиринтов нет.
Знаете ли вы один из самых прекрасных
древнегреческих мифов о победе Тесея над
Минотавром?
Критский царь Минос приказал знаменитому
художнику и архитектору Дедалу построить
лабиринт. В этот лабиринт, с бесчисленными
коридорами, тупиками и переходами, Минос поселил
Минотавра (кровожадное существо с человеческим
телом и головой быка) и потребовал у афинян,
убивших его сына, раз в девять лет присылать на
съедение чудовищу семерых сильнейших юношей и
семерых красивейших девушек. Их отводили в
лабиринт, и юные афиняне, блуждая там,
становились жертвами Минотавра. Когда афиняне
готовили кровавую дань в третий раз, сын
афинского царь Эгея, Тесей, задумал освободить
родной город от позорной обязанности. Вместе с
очередной группой жертв Минотавра он отправился
на Крит с целью убить чудовище. Дочь Миноса,
Ариадна, полюбила мужественного Тесея и дала ему
волшебный клубок, который помог ему найти выход
из лабиринта. Привязав конец нити у входа, Тесей
пошёл на поиски Минотавра. Поединок закончился
победой юноши, который затем, идя обратно по нити
Ариадны, вышел из лабиринта и вывел оттуда всех
обречённых.
А сможете ли вы найти выход из лабиринта?
Как можно достать из муравейника зёрнышко?
9. Практическая работа
Вырежьте из бумаги прямоугольник со сторонами
10 см и 16 см. Отрежьте от него квадрат со стороной 10
см. Останется прямоугольник, стороны которого 6
см и 10 см, т.е. одна больше другой тоже примерно в
1,6 раза. Затем от этого прямоугольника отрежьте
квадрат со стороной 6 см. останется
прямоугольник, одна сторона которого тоже
примерно 1,6 раза больше другой. Этот процесс
можно продолжать и дальше. На прямоугольники, в
которых стороны соотносятся приблизительно как
1,6 : 1, обратили внимание очень давно. Посмотрите
на изображение храма Парфенон в Афинах (см. рис1).

Даже сейчас это из самых красивых сооружений
мира. Этот храм построен в эпоху расцвета
древнегреческой математики. И его красота
основана на строгих математических законах. Если
мы опишем около фасада Парфенона прямоугольник,
то окажется, что длина его больше ширины примерно
в 1,6 раза. Такой прямоугольник называли Золотым
прямоугольником. Говорят, что его стороны
образуют золотое сечение.
10.
Числовыми выражениями зашифрован
фразеологический оборот. Значения выражений
замените буквами.
| 84 : 42 |
2 |
а |
| 75 : 15 |
5 |
в |
| 96 : 32 |
3 |
г |
| 90 : 10 |
9 |
и |
| 91 : 13 |
7 |
е |
| 55 : 11 |
5 |
в |
| 96 : 8 |
12 |
ы |
|
|
 |
| 88 : 11 |
8 |
к |
| 90 : 15 |
6 |
о |
| 60 : 6 |
10 |
н |
| 53 : 53 |
1 |
ю |
| 92 : 23 |
4 |
ш |
| 77 : 7 |
11 |
н |
| 63 : 7 |
9 |
и |
|
Знаете ли вы, в каком смысле употребляют этот
фразеологический оборот?
По преданию, в Древней Греции жил царь Авгий. Он
был страстным любителем лошадей. В его конюшнях
стояло несколько тысяч лошадей. Стойла, в которых
стояли эти лошади, не чистились в течение
тридцати лет, по самые крыши они заросли навозом.
Однажды на службу к царю Авгию поступил
сказочный силач Геракл, которому царь поручил
очистить конюшни. Геракл был не только могуч и
силён, но и умён. Он отвёл в ворота конюшни реку, и
бурный поток вымыл оттуда всю грязь.
Выражение “авгиевы конюшни” мы
употребляем, когда хотим сказать о крайней
запущенности, загрязнённости.
11. Отношения и пропорции (сок)
Ученые в Древней Греции не признавали дробных
чисел и из-за этого у них возникали затруднения с
измерением величин. Греческий математик не мог
сказать, что длина одного отрезка втрое больше
длины другого отрезка. Ведь эти длины могли
оказаться дробными числами, а то и вообще не
выражаться известными грекам числами, а потому
применять к ним операцию умножения было нельзя.
Пришлось греческим ученным придумать способ, как
обходиться в науке без того, чтобы выражать
длины, площади и объемы числами. Так было создано
учение об отношениях величин, о равенстве таких
отношений.
Приготовим апельсиновый (гранатовый) напиток.
Мы можем налить в кувшин два стакана сока и три
стакана воды. Т.е. мы смешиваем ингредиенты т.е.
составные части напитка, в отношение 2 к 3.
Можно брать больше количества того или иного
ингредиента, но если пропорции при этом не
меняются, вкус напитка также не изменяется. (Все
дети готовят и пьют сок).
Заключение:
Итак, подведем итоги (анкета, на листиках
отвечаем на вопросы).
- Какие науки учащиеся изучали в школе Пифагора? (Математика,
музыка).
- В какое время жил Диофант? (Он жил в III в.н.э.)
- Что рассказала о Диофанте надгробная надпись на
камне? (Диофант жил 84 года).
- Какое выражение мы употребляем, когда хотим
сказать о крайней запущенности, загрязненности?
(Авгиевы конюшни).
- Кто из богинь самая прекрасная? (Афродита).
- Что означает слово “Лабиринты”? (Ходы в
подземельях).
- Каких греческих ученных вы запомнили? (Платон,
Евклид, Архимед, Гипсикл, Герон, Эратосфен,
Гипатия).
Заключительные строки задачи Архимеда быках
Солнца.
“Если ты это найдешь чужестранец, умом
пораскинув, и сможешь точно назвать каждого
стада число, то уходи, возгордившись победой, и
будет считаться, что в этой мудрости ты все до
конца превзошел.”
Если от математики Древнего Востока до нас
дошли отдельные, задачи с решениями и таблицами,
то в Древней Греции рождается наука математика,
основанная на строгих доказательствах. Этот
важнейший скачок в истории науки относится к VI –
V вв. до н.э.
xn--i1abbnckbmcl9fb.xn--p1ai Старинные задачи - Математика без скукиВ древних рукописях и старинных учебниках арифметики разных стран встречаются много интересных задач на дроби. Решение каждой из таких задач требует немалой смекалки, сообразительности и умения рассуждать. Рассмотрим несколько таких задач.  Задача 1 Задача 1Путник, догнав другого, спросил его: «Далеко ли до деревни, которая впереди?» Другой путник ответил: « Расстояние от деревни, из которой ты идёшь, равно трети всего расстояния меду деревнями. А если пройдёшь ещё две версты, будешь ровно посередине между деревнями. Сколько вёрст осталось идти первому путнику? Решение: 2 версты, которые нужно пройти до середины, составляют 1/6 всего расстояния до деревни. 2*6=12( вёрст) всё расстояние 12*1/3=4( версты) прошёл путник 12-4=8 (вёрст) осталось Ответ: 8 вёрст.  Задача 2 Из папируса Ахмеса (Египет, ок. 2000 лет до н.э.). Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты из своего многочисленного стада? Пастух отвечает: - Я привожу две трети от трети скота. Сочти, сколько быков в стаде? Решение: 70 быков составляют 2/3 от 1/3 1) 2/3*1/3=2/9 составляют 70 быков. 2) 70 : 2/9= 315(быков) составляют стадо. Ответ: 315 быков  Задача 3 Китай, II век н.э. Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моя до южного моря летит 9 дней. Теперь утка и гусь вылетают одновременно. Через сколько дней они встретятся? Решение: утка 7 дн. 9 раз 63 дня, гусь 9 дн. 7 раз 63 дня 1)7+9=16 раз 2) 63:16= 3 15/16 ( дней) 1) 1:7=1/7 пути утка 1 д. 2) 1:9=1/9 пути гусь 1 д. 3) 1/7+1/9=16/63 вместе 4) 1:16/63=3 15/16 дней Ответ: через 3 15/16 дней.  Задача 4 Из книги «Косс» Адама Ризе (XVI в.) Задача 4 Из книги «Косс» Адама Ризе (XVI в.)sites.google.com «Математические задачи Древней РУСИ». | Социальная сеть работников образованияСлайд 1 Исследовательская работа по математике по теме: «Математические задачи Древней Руси» Автор : Сухорукова Любовь, ученица 6б класса, МБОУ «СОШ №8» Руководитель: Купавцева Н.В.Слайд 2 ЭПИГРАФ «Слава нашей стороне! Слава нашей старине! Колесо истории мы повернем И рассказывать начнем, Чтобы все вы знать могли О делах родной земли». …незнание прошлого неизбежно приводит к непониманию настоящего. Слайд 3 АКТУАЛЬНОСТЬ Знание истории предмета помогает лучше его познать и изучить. Просто каждый человек обязан знать историю. Слайд 4 Моя основная цель: Выявить особенности математических задач Древней Руси и возможные способы их решения в современной практике решения задач. Слайд 5 задачи: Изучить историю возникновения науки математики в Древней Руси. Показать значимость древнерусских математических задач. Сопоставить древнерусские математические задачи с современной математикой. Составить подборку древнерусских задач . Слайд 6 . Моя гипотеза Если раскрыть секреты исторических древнерусских математических задач, то постижение современных теорий и формул станет более интереснее и увлекательнее. Слайд 7 Немного из истории.. Предки русского народа — славяне — с незапамятных времён жили на землях Средней и Восточной Европы. У славян, как и у всех других народов, первым учителем математики была жизнь, практика . Слайд 8 В хозяйственной жизни далекого прошлого люди обходились сравнительно небольшими числами – так называемым малым счетом наших предков. Он доходил до числа 10000, которое в самых старых памятниках называется “тьма” Слайд 9 Старинная рукопись по этому случаю заявляет, что “больше сего числа несть человеческому разуму разумети ”. 1 060 м Слайд 10 В 1134 году новгородский монах Кирик написал сочинение «...о том, как узнать человеку числа всех лет». Это самый древний дошедший до нас письменный памятник славянской математики . Слайд 11 Старинная задача № 1 “Некий человек нанял работника на год, обещав ему дать 12 рублев и кафтан. Но тот, проработав 7 месяцев, восхотел уйти и просил достойной платы с кафтаном. Он же (хозяин) дал ему по достоинству расчет 5 рублев и кафтан, и знать надлежит, какой цены оный кафтан был”. Слайд 12 Можно вычислить по действиям, рассуждая логически. Работник получил 12 – 5 = 7 (руб.) за 12 – 7 = 5 (месяцев), поэтому за один месяц ему платили 7:5 = 1,4 (руб.), а за 7 месяцев он получил 7 ·1,4 = 9,8 (руб.), тогда кафтан стоил 9,8 – 5 = 4,8 (руб.). Слайд 13 2 способ решения. Пусть x руб. — стоимость кафтана. Алгебраическое решение задачи приводит к уравнению, применяя основное свойство пропорции. (x + 12):12 = = (x + 5):7 Х = 4,8 . Итак, кафтан стоил 9,8 – 5 = 4,8 ( руб ). Слайд 14 Старинная задача №2 Говорит дед внукам: «Вот вам 130 орехов. Разделите их на 2 части так, чтобы меньшая часть, увеличенная в 4 раза, равнялась бы большей части, уменьшенной в 3 раза». Как разделить орехи? Слайд 15 I способ Уменьшив втрое количество орехов в большей части, мы получим их столько же, как в четырех меньших частях. значит, большая часть должна содержать в 3X4= 12 раз больше орехов, чем меньшая, а общее число орехов должно быть в 13 раз больше, чем в меньшей части. Поэтому меньшая часть должна содержать 130:13=10 орехов, а большая 130 — 10 = 120 орехов. Слайд 16 II способ Пусть x орехов в меньшей части. Алгебраическое решение задачи приводит к уравнению 4х:1=(130-х):3 х = 10. Итак, меньшая часть должна содержать 130:13=10 орехов, а большая 130 — 10 = 120 орехов. Слайд 17 Была проведена анкета по выявлению сохранения интереса к старинным задачам Древней Руси. Было опрошено 56 человек, среди них 25 учащихся МОУ «СОШ №8» , 20 человек – старше 40 лет и 16 человек в возрасте от 18 до 40 лет. Каждому из них было задано 3 вопроса. Слайд 18 Знакомы ли вы со старинными задачами Древней Руси? Слайд 19 Можете ли вспомнить интересные математические задачи древности? Слайд 20 Как вы считаете, должны люди знать старинные задачи? Слайд 21 Моя гипотеза подтвердилась. Знание истории развития науки математики и постижение способов решения исторических задач помогает изучению данной увлекательной науки. Слайд 22 Вывод: Проведенная работа мне была интересна. Я ближе познакомилась со старинными русскими задачами. Выявила связь между способами решения старинных математических задач и сопоставила древнерусские математические задачи с современной математикой. Анкетные данные показывают , что подрастающее поколение недостаточно знакомо со старинными математическими задачами, а значит актуальна тема моего исследования . Слайд 23 Спасибо за внимание!!! nsportal.ru игра-путешествие "Старинные задачи через века и страны"  Разделы: Математика Цели и задачи:
- Показать учащимся развитие математической
мысли с древнейших времен, уточнить и
систематизировать разрозненные сведения по
истории математики.
- Развивать логическое мышление учеников, умение
применять свои знания в нестандартной ситуации.
- Формировать интерес к математике,
любознательность и желание самостоятельно
пополнять свои знания.
Оборудование: Для проведения
мероприятия необходимо иметь локальную
компьютерную сеть, в которой размещена
презентация.
Правила игры:
- В игре участвуют несколько команд (например, от
каждого класса одной параллели) по 4-5 человек в
команде.
- Каждая команда обеспечена 1-2 компьютерами.
- По сигналу о начале игры команды “отправляются
в путешествие” по любому из предложенных
маршрутов (открыть Слайд3 в презентации и нажать
соответствующую выбранному маршруту кнопку).
- В течение 30 минут команды произвольно переходят
от одной условной станции к другой, стараясь
решить максимальное количество предложенных
задач и познакомиться с историческим материалом.
- По сигналу об окончании игры команды сдают жюри
свои решения.
- В течение 10 минут жюри подводит итоги, начисляет
баллы за решенные задачи и определяет
победителей и призеров.
- Команды в это время выполняют тест, содержание
которого отражает сведения из истории
математики, полученные в процессе путешествия. В
это же время они могут открыть страницу с
ответами, подсказками, решениями всех задач.
- Итог игры подводится окончательно по общей
сумме баллов за задачи и тест.
Содержание игры.
Маршруты путешествия:
- Древний Египет.
- Вавилон.
- Древняя Греция.
- Китай.
- Индия.
- Страны Ислама.
- Страны Европы.
- Россия.
Презентация
1. Древний Египет.
Самый большой, сохранившийся до наших дней,
древнеегипетский математический текст – это так
называемый папирус XVIII-XVII вв. до н. э. Ахмеса.
Около пяти тысяч лет назад при фараоне Джосере
был признан богом мудрости великий врачеватель,
государственный деятель и первый известный нам
по имени математик Имхотеп.
Математические правила, нужные для земледелия,
астрономии и строительных работ, древние
египтяне записывали на стенах храмов или на
папирусах. Еще 4 тыс. лет назад они решали
практические задачи по арифметике, алгебре и
геометрии, причем в арифметике пользовались не
только целыми числами, но и дробями.
Задачи из папируса Ахмеса.
1. У семи лиц по семи кошек, каждая кошка съедает
по семи мышей, каждая мышь съедает по семи
колосьев, из каждого колоса может вырасти по семи
мер ячменя. Как велики числа этого ряда и их
сумма?
2. Раздели 10 мер хлеба на 10 человек, если
разность между количеством хлеба у каждого
человека и ему предшествующего составляет 1/8
меры.
3. Найти приближенное значение для числа ,приняв
площадь круга равной площади квадрата со
стороной 8/9 диаметра круга.
2. Вавилон.
В Древнем Вавилоне математика зародилась
задолго до нашей эры. Вавилонские памятники в
виде глиняных плиток с клинописными надписями
хранятся в различных музеях мира.
Вавилоняне были основоположниками астрономии,
создали шестидесятиричную систему счисления,
решали уравнения второй степени и некоторые виды
уравнений третей степени при помощи специальных
таблиц
Задачи Древнего Вавилона
4. Задача на глиняной табличке(ок. 1950 до н. э.)
Площадь А, состоящая из суммы площадей двух
квадратов, составляет 1000. Сторона одного из
квадратов составляет уменьшенные на 10 две трети
стороны другого квадрата. Каковы стороны
квадратов?
5. Задача о вычислении числа П
За длину окружности вавилоняне принимали
периметр вписанного в эту окружность
правильного шестиугольника. Найти приближение
для П, которым пользовались вавилоняне.
6, Задача о шесте
Найти длину шеста, сначала вертикально
прислоненного к стене, затем смещенного так, что
его верхний конец опустился на 3 локтя, причем
нижний конец отступил от стены на 9 локтей.
7. Задача о делении прямого угла
Разделить прямой угол на три равные части.
3.Древняя Греция.
Если от математики Древнего Востока до нас
дошли отдельные задачи с решениями и таблицы, то
в Древней Греции рождается наука математика,
,основанная на строгих доказательствах Э.тот
важнейший скачок в истории науки относится к VI-V
вв. до н. э.
Задачи Древней Греции
Задачи Пифагора
Первое построение геометрии как дедуктивной
науки принадлежит Пифагору Самосскому (ок. 570 -500
г. до н. э.) – древнегреческому математику и
философу.
8. Всякое нечетное число, кроме единицы, есть
разность двух квадратов.
9. Разрезать крест на четыре части и сложить из
получившихся частей квадрат (рисунок 1).
10. Задача “Суд Париса”
Богини Гера, Афродита и Афина пришли к юному
Парису, чтобы тот решил, кто из них прекраснее,
высказав следующие утверждения:
АФРОДИТА. Я самая прекрасная.
АФИНА. Афродита не самая прекрасная.
ГЕРА. Я самая прекрасная.
АФРОДИТА. Гера не самая прекрасная
АФИНА. Я самая прекрасная.
Все утверждения прекраснейшей из богинь
истинны, а все утверждения двух остальных богинь
ложны. Кто прекраснее из богинь.
11. Задачи Евклида
В III в. до н. в трудах знаменитого математика
Евклида, написавшего 13 книг под общим названием
“Начала”, древнегреческая геометрия достигла
своего апогея.
- На данном отрезке АВ построить равносторонний
треугольник.
- Разделить произвольный угол на две равные
части.
Мул и осел под вьюком по дороге с мешками
шагали.
Жалобно охал осел, непосильною ношей придавлен.
Это подметивший мул обратился к попутчику с
речью:
“Что ж, старина, ты заныл и рыдаешь, как будто
девчонка?
Нес бы вдвойне я, чем ты, если б отдал одну ты мне
меру,
Если ж бы ты у меня лишь одну взял, то мы бы
сравнялись”.
Сколько нес каждый из них, о геометр, поведай нам
это.
12. Задачи Архимеда
Древнегреческий ученый Архимед (ок. 287-212 гг до н.
э.) – математик, механик и астроном.
- Доказать, что площадь круга, описанного около
квадрата ,вдвое больше площади вписанного в
квадрат круга.
- Найти сумму квадратов n первых чисел
натурального ряда.
4. Китай.
Возникновение китайской цивилизации на
берегах реки Хуанхэ относится к началу II тыс. до
н. э.
Среди важнейших достижений китайской
математики отметим: правило двух ложных
положений, введение отрицательных чисел,
десятичных дробей, методов решения систем
линейных уравнений, алгебраических уравнений
высших степеней и извлечение корней любой
степени.
Задачи древнего Китая
13. Задача Ло-шу
Заполнить натуральными числами от 1 до 9
квадратную таблицу размером 3х3 так, чтобы суммы
чисел по всем строкам, столбцам и диагоналям были
равны одному и тому же числу 15
Задача Сунь-цзы (III-IV вв.)
Имеются вещи, число их не известно. Если считать
их тройками, то остаток 2; если считать их
пятерками, то остаток 3; если считать их
семерками, то остаток 2. Спрашивается, сколько
вещей.
15. Задача Чжан Цюцзяня (V в.)
1 петух стоит 5 цяней, 1 курица стоит 3 цяня, 3
цыпленка стоят 1 цянь. Всего на 100 цяней купили 100
птиц. Спрашивается, сколько было в отдельности
петухов, кур, цыплят.
16. Задача Цзу Чун-Чжи
Найти наилучшую обыкновенную дробь к числу  , если , если
3,1415926<  <
3,1415927 <
3,1415927
5. Индия.
Творчество индийских математиков оказало
огромное влияние на развитие арифметики
(индийская десятичная позиционная нумерация),
алгебры (метод рассеивания для неопределенных
уравнений первой и второй степени с двумя
неизвестными) и тригонометрии (бесконечные ряды
для синуса, косинуса и арктангенса).
Задачи Древней Индии
17. Задача Брахиагупты
Найти высоту свечи, зная длины теней,
отбрасываемых вертикальным шестом в двух
различных положениях, и расстояние между ними
(рисунок 2).
18. Задача-легенда
Изобретатель шахмат, которому было предложено
запросить любую награду, попросил положить ему в
награду на первую клетку шахматной доски одно
зерно, на вторую – 2 зерна, на третью – 4 зерна и т.
д. Сколько зерен запросил мудрец?
19. Задача Магавиры
Найти число павлинов в стае, 1/16 которой,
умноженная на себя, сидит на манговом дереве, а
квадрат 1/9 остатка вместе с 14 другими павлинами –
на дереве тамала.
20. Задача
О друг, назови число различных ожерелий,
которые можно получить из бриллиантов, сапфиров,
изумрудов, кораллов и жемчугов.
6. Страны Ислама.
Крупнейшие ученые средневековья – ал-Хорезми,
Авиценна, ал-Бируни, Омар Хайям, ал-Каши писали
свои сочинения на арабском языке. Употребляемые
нами термины “арабские цифры”, “корень”,
“алгебра”, “алгоритм”, “синус”
сформировались под влиянием науки стран Ислама.
Задачи стран Ислама.
21. Задача из сказки “1001ночь”
Стая голубей подлетела к высокому дереву. Часть
голубей села на ветвях, а другая расположилась
под деревом. Сидевшие на ветвях говорят
расположившимся внизу: “Если бы один из вас
взлетел к нам, то вас стало бы втрое меньше, чем
нас всех вместе, а если бы один из нас слетел к
вам, то нас стало бы поровну”. Сколько голубей
сидело на ветвях и сколько под деревом?
22. Задача ал-Каши (XV в.)
Плата работнику за месяц, то есть за тридцать
дней, - десять динаров и платье. Он работал три дня
и заработал платье. Какова стоимость платья?
23. Задача Ибн Сины (Авиценны, X-XI вв.)
Если число, будучи разделено на 9, дает в остатке
1 или 8, то квадрат этого числа, деленный на 9, дает
в остатке 1. Какое это число?
7. Страны Европы.
В середине I тыс. в Европе центрами просвещения
сначала были монастыри, а позднее университеты.
Развитие торговли, мореплавания, ремесел
повысило роль математики. В XVII в.была создана
аналитическая геометрия. В XVIII столетии
появилось дифференциальное и интегральное
исчисление. Научная деятельность крупнейших
математиков сосредоточилась в прославленных
академиях в Париже, Петербурге и Берлине.
Задача народов Европы.
24. Задача Леонарда Пизанского (итальянский
математик Л. Пизанский (1180-1240) по прозвищу
Фибоначчи).
30 птиц стоят 30 монет, куропатки стоят по 3
монеты, голуби - по две и пара воробьев - по монете;
спрашивается, сколько птиц каждого вида.
25. Французская задача 17 век.
Трое имеют по некоторой сумме каждый. Первый
дает из своих денег двум другим столько, сколько
есть у каждого. После него второй дает двум
другим, столько, сколько каждый из них имеет.
Наконец, и третий дает двум другим столько,
сколько есть у каждого. После этого, у всех троих
оказывается по 8 экю. Спрашивается, сколько денег
было у каждого.
26. Задача Исаака Ньютона.
И. Ньютон (1643-1727) – величайший английский физик
и математик, разработал дифиринциальное и
интегральное исчисление.
Даны 3 последовательных члена геометрической
прогрессии. Их сумма равна 19, а сумма их квадратов
133. Определить эти 3 члена.
27. Задача Г. В. Лейбница
Лейбниц (1646-1716) – немецкий философ, математик,
физик и изобретатель.
Показать, что если
n – целое число, то n5 – n делится на 5.
28. Задача Этьенна Безу.
Французский математик Безу (1730-1783) занимался
исследованием свойств систем уравнений высших
степеней и доказал теорему о делении многочленов
на линейный двучлен.
По контракту работникам причитается по 48
франков за каждый отработанный день, а за каждый
не отработанный день с них взыскивается по12
франков. Через 30 дней выяснилось, что работникам
ничего не причитается. Сколько дней они
отработали в течение этих 30 дней.
8. Россия.
Первые сведения о развитие математики на Руси
относится к IX – XII вв. (древнерусская нумерация,
метрология, первые системы дробей и др.). Рассвет
математики и механики в России связано с
основанием Петербургской академии наук (XVIII в.) и
с именами великих ученых: М. В. Ломоносова,
Леонарда Эйлера, П. Л. Чебышева, Н. И. Лобачевского,
С. В. Ковалевской и др.
Нестареющие отечественные задачи.
29. Старинная народная задача.
Шли 7 старцев
У каждого старца по 7 костылей
На каждом костыле по 7 сучков
На каждом сучке по 7 кошелей
На каждом кошеле по 7 пирогов
В каждом пироге по 7 воробьев.
Сколько всего.
30. Задачи Л.Ф. Магницкого.
Русский математик и педагог Л. Ф. Магницкий
(1669-1739) – автор первого русского учебника по
математике, названного Л. М. Ломоносовым
“вратами учености”.
Один человек выпьет кадь пития в 14 дней, со
женою выпьет тое же кадь в 10 дней, и ведательно
есть, в колико дней жена его особо выпьет тое же
кадь.
31. Задача Леонарда Эйлера.
Л. Эйлер (1707-1783), именем которого названы
теоремы, уравнения, формулы и т. д., обрел в России
вторую родину и проработал в Петербургской
академии наук более 30 лет.
Некий чиновник купил лошадей и быков за 1770
талеров. За каждую лошадь он уплатил по 31 талеру,
а за каждого быка по 21 талеру. Сколько лошадей и
быков купил чиновник?
32. Задача Л. Н. Толстого.
Артели косцов надо было скосить два луга, один
вдвое больше другого. Половину дня артель косила
большой луг. После этого артель разделилась
пополам: первая половина осталась на большом
лугу и докосила его к вечеру до конца; вторая я же
половина косила малый луг, на котором к вечеру
остался участок, скошенный на другой день одним
косцом за один день работы. Сколько косцов было в
артели?
Приложение 1
Приложение 2
Тест
Cписок используемой литературы
- Баврин И.И., Фрибус Е.А. Занимательные задачи по
математике. – М: ВЛАДОС, 1999.
- Пичурин Л.Ф. За страницами учебника алгебры. –
М.: Просвещение, 1999.
- Фокин Б.Д. Арифметика: Сборник занимательных
задач для 5-6 классов. – М.: АРКТИ, 2000.
- Игнатьев Е.И. В царстве смекалки.- М.:Наука,1982.
- Перельман Я.И. Занимательная алгебра.- М.: Наука.
1975.
xn--i1abbnckbmcl9fb.xn--p1ai Проектная работа на тему "Старинные математические задачи" (7 класс) 
Проектная работа Старинные математические задачи Выполнили учащиеся 7 класса Руководитель: Заугарова В.А. Цели и задачи проекта. 1. Развитие творческого потенциала учащихся. 2. Развитие информационной культуры. 3. Формирование самостоятельности в сфере исследовательской деятельности. 4. Формирование умения решать старинные задачи разных стран. 5. Закрепление знаний по математике. 6. Повышение интереса к математике. Содержание проекта Задачи Древнего Египта. Задачи Вавилона. Задачи Древнего Китая. Задачи Древней Индии. Задачи Древней Руси.
Пояснительная записка Выбор темы данного проекта обьясняется тем, что учащиеся имеют большой интерес к задачам древности, способам их решения. Позволяет показать связь истории и математики. Работа носит обучающий, практический характер. Задачи Древнего Египта 
Наиболее древние письменные математические тексты датируются примерно началом II тыс. до н. э. математические документы сохранились только в Египте, Вавилоне, Китае и Индии. Около пяти тысяч лет назад при фараоне Джосере был признан богом мудрости великий врачеватель, государственный деятель и первый известный нам по имени математик Имхотен. Математические правила, нужные для земледелия, астрономии и строительных работ, древние египтяне записывали на стенах храмов или на папирусах. Еще IX тыс. лет назад они решали практические задачи по арифметике, алгебре и геометрии. Задача 1. У семи лиц по семи кошек, каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа из этого ряда и их сумма? Задача 2. Найти приближенное значение для числа π, приняв площадь круга равной площади квадрата со стороной  диаметра круга. диаметра круга. Задачи Вавилона  В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством. В древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 50000, причем из них примерно лишь 150 с текстами математичес- ких задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира. В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с землемерием, торговлей и строительством.
Вавилоняне были основоположниками астрономии, создали шестидесятеричную систему счисления, решали уравнения второй степени, некоторые виды уравнений третей степени. Задача 3. О глиняной табличке. Площадь А, состоящая из суммы площадей двух квадратов, составляет 1000. Сторона одного из квадратов составляет уменьшенные на две трети стороны другого квадрата. Каковы стороны квадратов?  Задача 4 Разделить прямой угол на три равные части. Задачи Древней Греции  Если от математики Древнего Востока до нас дошли отдельные задачи с решениями и таблицами, то в Древней Греции рождается наука математика, основанная на строгих доказательствах. Этот важнейший скачок в истории относится к VI-V вв. до н. э. Задача 5. «Суд Париса» Один из древнейших мифов содержит сказание троянского царевича Париса…Однажды на свадьбе богиня раздора Эрида подбросила собравшимся гостям яблоко с надписью «прекраснейшая». Из-за этого яблока возник спор между богиней мудрости и справедливой войны Афиной, богиней любви и красоты Афродитой и сестрой и супругой Зевса Герой. Они обратились к царю и отцу богов и людей Зевсу, чтобы он решил, кому должно достаться яблоко. Зевс отправил богинь на гору к Парису, который пас там там свои стада. Парис должен был решить, какая из богинь самая прекрасная. Каждая из богинь старалась склонить юношу на свою сторону: Афина предлагала ему мудрость и военную славу, Афродита- красивейшую женщину на земле в жены. Гера- власть и богатство. Как Парис определил р из богинь, можно узнать, решив старинную задачу. Богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот решил, кто из них прекраснее. Представ перед Парисом, богини высказали следующие утверждения. Афродита. Я самая прекрасная. (1) Афина. Афродита не самая прекрасная (2) Гера. Я самая прекрасная. (3) Афина. Афродита не самая прекрасная. (4) Парис, прилегший отдохнуть на обочине дороги, не счел нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему нужно было решить, какая из них самая прекрасная. Парис предложил, что все утверждения прекраснейшей из богинь истинны, а утверждения двух остальных богинь ложны. Мог ли Парис вынести решение, кто прекраснее из богинь? Задача 6. Задача Дидоны. В древнем мифе рассказывается, что Тирский царь Пигмалион убил Сихея, мужа своей сестры Дидоны, чтобы овладеть его богатством. Дидона, покинув Финикию, после многих приключений оказалась в Северной Африке. Король нумидийцев Ярт обещал подарить Дидоне участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Хитрая Дидона разрезала воловью шкуру на тонкие полоски, связала из них очень длинную веревку и отмерила большой участок земли, на котором основала город Карфаген. Участок какой формы окружила Дидона веревкой данной длины, чтобы получить наибольшую площадь? Задача 7. О школе Пифагора. Пифагор Самосский (ок. 570- ок.500 г. до н. э.)- древнегреческий математик и филосов. Основал пифагорейский союз (школу). Пифагорейцы занимались астрономией, геометрией, гармонией (теорией музыки) и арифметикой (теорией чисел). В школе возникло представление о шарообразности Земли. Тиран острова Самос Поликрат однажды спросил на пиру у Пифагора, сколько у того учеников. Охотно скажу тебе, о Поликрат,- отвечал Пифагор. Половина моих учеников изучает прекрасную математику, четверть исследует тайны вечной природы, седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Сколько учеников веду я к рождению вечной истины? Задача 8. Всякое нечетное число, кроме единицы, есть разность двух квадратов. Задача 9. Три грации имели по одинаковому числу плодов и встретили девять муз. Каждая из граций отдала каждой из муз по одинаковому числу плодов. После этого у каждой из муз и каждой из граций стало по одинаковому числу плодов. Сколько плодов было у каждой из граций до встречи с музами? Задача 10. Мул и осел под вьюком по дороге с мешками шагали. Жалобно охал осел, непосильною ношей придавлен. Это подметивший мул обратился к сопутчику с речью: «Что ж , старина, ты заныл и рыдаешь, будто девчонка? Нес бы вдвойне я, чем ты, если б отдал одну ты мне меру, Если ж бы ты у меня лишь одну взял, то мы бы сравнялись» Сколько нес каждый из них, о геометр, поведай нам это. Задача 11. Герона Александрийского. Из под земли бьют четыре источника. Первый заполняет бассейн за один день,- второй- за два дня, третий- за четыре дня. Сколько времени наполнят бассейн все четыре источника вместе? Задача 12. Древнеримская задача (II в.) Некто, умирая, завещал: « Если у моей жены родится сын, то пусть ему будет дано 2:3 имения, а жене – остальная часть. Если, же родится дочь, то ей  , а жене , а жене  ». Родилась двойня - сын и дочь. Как разделить имение? ». Родилась двойня - сын и дочь. Как разделить имение?  Задачи Древнего Китая 
Возникновение китайской цивилизации на берегах реки Хуанхе относиться к началу II тыс. до н. э. Сохранились обозначения цифр на гадальных костях животных XIII в. до н. э. Среди важнейших достижений китайской математики отметим: введение отрицательных чисел, десятичных дробей, методов решения систем линейных уравнений, уравнений высоких степеней. В Китайских рукописях содержатся наиболее ранние сведения о магических (волшебных) квадратах (V в. до н.э.). Задача 13. Заполнить натуральными числами от 1 до 9 квадратную таблицу размером 3X3 так, чтобы суммы чисел по всем строкам, столбцам и диагоналям были равны одному и тому же числу 15. Задача 14. Имеются вещи, число их неизвестно. Если считать их тройками, то остаток 2; если считать их пятерками, то остаток 3; если считать их семерками, то остаток 2. Спрашивается, сколько вещей. Задачи Древней Индии  Задача 15. Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи каково число их разновидностей? Задача 16. Прекрасная дева с блестящими очами, скажи мне величину такого числа, которое, будучи умножено на 3, затем увеличено на 3:4 этого произведения, разделено на 7, уменьшено на 1:3 частного, умножено само на себя, уменьшено на 52, после извлечения квадратного корня, прибавления 8 и деления на 10, дает число 2. Задачи Древней Руси  Задача 17. Три торговца, не желая отбивать друг у друга покупателей, решили продавать свои апельсины по одинаковой цене. У одного торговца было 50 апельсинов, у другого 30, у третьего только 10. Торговцы условились, что цену можно изменить, лишь бы продажа одновременно производилась у всех трех торговцев по одной и той же цене. Когда весь товар был распродан, то оказалось, что каждый из торговцев выручил за свои апельсины одинаковую сумму, а именно 50 копеек. Как и по какой цене они должны были продать апельсины? Задача 18. Сельский виноторговец призвал трех своих сыновей и велел поделить им поровну между собой 7 полных бочонков с вином, 7 таких же бочонков, наполненных вином поровну, и 7 таких же бочонков, но пустых. Как сыновья могут поделить вино и бочонки, чтобы каждому досталось и одинаковое количество вина, и одинаковое число бочонков, если переливать вино из одного бочонка в другой нельзя? Задача 19. На скотном дворе гуляли гуси и поросята. Хозяин двора и его сын вышли на двор, посмотрели на живность и пошли в поле. По дороге сын и спрашивает: «Папа, сколько у нас на скотном дворе гусей и сколько поросят?» - «А вот угадай-ка сам. Если считать по головам, то на дворе 25 голов, а если по ногам, то 70 ног». Сколько было гусей и сколько поросят? Задача 20. Хозяйка в продолжение поста накопила два горшка масла: один в 8 фунтов, другой в 3 фунта, а третий горшок в 5 фунтов остался у нее пустым. Перед праздником хозяйке понадобилось одолжить 6 фунтов масла соседке. Как она это сделала, если меркой могли служить только те же три горшка? Задача 21. Дед, отец и сын встретили во время прогулки знакомого, который спросил, сколько каждому из них лет. «Нам 131 год и 10 месяцев», - ответил за всех дед и важно зашагал вперед. Тогда их знакомый, продолжая интересоваться их возрастом, спросил отца: «Ну скажите же, сколько вам лет?»- «Мне вместе с сыном 57 лет и 2 месяца,- ответил отец,- а сын на 19 лет и 10 месяцев моложе меня». Так знакомому и не пришлось узнать, сколько лет каждому из них. Сколько лет деду, отцу и сыну? Решения задач 1. 7; 49; 343; 2401; 16807; 19607. 2.По условию задачи 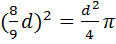 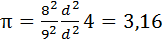 . .
3. 30 и 10. 4. Пусть требуется разделить прямой угол ABC на три равные части. Для этого древние вавилоняне на отрезке AD стороны BA строили равносторонний треугольник BED. Тогда угол CBE будет составлять одну треть данного прямого угла. Остается только разделить пополам угол DBE, и задача будет решена. С  
A D E  В 5. Пусть Парис предложил, что Афина изрекла истину. Тогда она прекраснейшая из богинь, и по предложению утверждение (4) ложно. Мы приходим к противоречию, т.к. Гера не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Афина. Таким образом, исходное предложение ложно. Если Парис предложит, что истину изрекла Гера, то она прекраснейшая из богинь, и по предложению (2) ложно. Мы снова приходим к противоречию, т. к. Афродита не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Гера. И это исходное предложение ложно. Если Парис наконец предложит, что Афродита изрекла истину, то Афродита прекраснейшая из богинь. Отрицания утверждений (2), (3), (5) истинны и показывают, что Афродита – прекраснейшая из богинь. 6. Среди всех плоских фигур данного периметра максимальную площадь имеет круг. Это замечательное свойство круга было известно в Древней Греции. Поэтому Дидона окружила имевшейся веревкой участок земли в форме полукруга с центром на берегу моря. 7. Среди 28 учеников школы Пифагора математикой занимались 14, музыкой – 7, пребывали в молчании – 4 и было еще 3 женщины. 8. 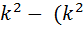 - 1) = 2k – 1 – нечетное число. - 1) = 2k – 1 – нечетное число. 9. Пусть у каждой из грации было по x плодов и они отдали каждой из муз по y плодов. Тогда по условию задачи должно быть x – y = 3y или x = 12y, т. е. у каждой грации до встречи с музами число плодов было кратно 12. 10 . Если x – груз мула, то (x-1) – груз осла, увеличенный на единицу, а следовательно, первоначальный груз осла был (x-2). С другой стороны x+1 в два раза больше, чем груз осла, уменьшенный на 1, т. е. x-3. Таким образом, x+1 = 2(x – 3) x=7 – груз мула, x-2=5 –груз осла. 11. 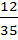 дня. дня. 12. Имение следует разделить между сыном женой и дочерью пропорционально числам 4:2:1. 13. 4 9 2 3 5 7 8 1 6 14. 23 + 105t. 15. 23 разновидности. 16. Применив метод инверсии (правило обращения), получим; 1) 2  10 = 20; 2) 20 - 8 = 12 3) 10 = 20; 2) 20 - 8 = 12 3)  = 144; = 144; 4) 144 + 52 = 196; 5) 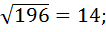 6) 14 6) 14 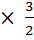 = 21; = 21; 7) 21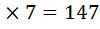 ; 8) 147 ; 8) 147 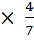 = 84; 9) 84 : 3 = 28. = 84; 9) 84 : 3 = 28. 17. Сначала торговцы решили продавать свои апельсины по 5 копеек за каждые 7 штук. Первый торговец продал 7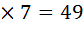 апельсинов и выручил 35 копеек. Второй торговец продал 7 апельсинов и выручил 35 копеек. Второй торговец продал 7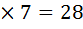 апельсинов и выручил 20 копеек. Третий торговец продал 7 апельсинов и выручил 20 копеек. Третий торговец продал 7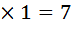 апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго – 2 апельсина, у третьего – 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек. апельсинов и выручил 5 копеек. После этого у первого торговца остался 1 апельсин, у второго – 2 апельсина, у третьего – 3 апельсина. Оставшиеся апельсины торговцы решили продать по 15 копеек за штуку. Первый торговец выручил 15 копеек, а всего 15 + 35 = 50 копеек. Второй торговец выручил 30 копеек, а всего 20 +30 = 50 копеек. Третий торговец выручил 45 копеек, а всего 45 + 5 = 50 копеек. 18. Каждый из сыновей должен получить по 7 бочонков. Все же вино можно представить себе так: 7 полных бочонков равны 14 полным наполовину бочонкам, плюс 7 полных наполовину бочонков, т.е. всего 21 полный наполовину бочонок. Следовательно, каждый из сыновей должен получить по 7 полных наполовину бочонков вина. Это можно сделать следующим образом: Полных Полных Пустых бочонков наполовину бочонков бочонков 1 сын 2 3 2 2 сын 2 3 2 3 сын 3 1 3 19. Так как голов 25, всех гусей и поросят 25 штук. Если бы на дворе гулял только одни гуси, то у них было бы 50 ног. На самом деле ног у всех обитателей скотного двора 70. Следовательно, «лишние» 20 ног принадлежат гулявшим на дворе поросятам, у каждого из которых на 2 ноги больше, чем у гуся. Значит, поросят было 20 : 2 = 10, а гусей 25 – 10 =15. 20. В 5-фунтовый горшок хозяйка доложила масла из 8-фунтового горшка, в котором осталось такое количество масла, которое требовалось. 21.Деду-74 года и 8 месяцев, отцу-38 лет и 6 месяцев, сыну-18 лет и 8 месяцев. infourok.ru Урок решения старинных задач  Разделы: Математика Цель урока:
- Повышение интереса учащихся к изучению
математики и углубление понимания темы действия
с дробями.
- Расширение умственного кругозора учащихся и
повышение их общей культуры.
Ход урока
Учитель. Ребята, вы уже знаете
натуральные и дробные числа, умеете складывать,
вычитать, умножать и делить дробные числа. А что
вы знаете об истории возникновения дробных
чисел?
Историческая справка о возникновении
дробных чисел. (Сообщение делает ученик.)
Решение старинных задач.
Задача 1.
Староиндийская задача с цветами и пчелами.
Индийцы широко употребляли “обыкновенные”
дроби. Наше обозначение обыкновенных дробей при
помощи числителя и знаменателя было принято в
Индии в VIII в.до н.э., однако
без дробной черты. Дробная черта стала
применяться лишь в XIII в.
Широко известны математики Древней Индии
Ариабхатта (V в.), Брахмагупта (VII в.), изложивший
правила действий с дробями, мало отличавшиеся от
наших, и Бхаскара (XII в.). Последний написал книгу
под названием “Лилавати”, т. е. “Прекрасная”
(наука арифметика).
Индийские ученые нередко излагали
арифметические задачи в стихах. Решим одну
древнеиндийскую задачу (математика Сриддхары XI
в.)
“Есть “кадамба” цветок,
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на Кутай посади.
Лишь одна не нашла
Себе места нигде
Все летала то взад, то вперед и везде
Ароматом цветов наслаждаясь.
Назови теперь мне,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось”.
Решение.
1)  2) 2) 
Ответ: 15.
Задача 2.
Л.Ф Магницкий из учебника “Арифметика”, книга
была создана в 1703 г.
Воз сена.
Лошадь съедает воз сена за месяц, коза за два
месяца, овца за три месяца.
За какое время лошадь, коза и овца вместе съедят
такой же воз сена.
Решение.
Поскольку лошадь съедает воз сена за месяц, то
за год (12 месяцев) она съедает 12 возов сена. Так
как коза съедает воз сена за 2 месяца, то за год
она съедает 6 возов сена. И, наконец, поскольку
овца съедает воз сена за 3 месяца, то за год она
съедает 4 воза сена. Вместе же они за год съедят
12+6+4=22 воза сена. Тогда один воз сена они вместе
съедят за 12:22=6/11 (шесть одиннадцатых) месяца.
Задача 3.
Великий русский писатель Лев Николаевич
толстой (1828-1910) проявлял особый интерес к
математике и ее преподаванию, много лет
преподавал начала математики в основанной им же
знаменитой Яснополянской школе, написал
оригинальную “Арифметику” и “Руководства для
учителя”. Своим гостям Л.Н. Толстой нередко
предлагал многие интересные задачи, среди
которых находится и следующая.
Задача Л.Н. Толстого. “Косцы должны
выкосить два луга. Начав с утра косить большой
луг, они после полудня разделились: одна половина
осталась на первом лугу и к вечеру его докосила, а
другая перешла косить на второй луг площадью
вдвое меньше первого. Сколько было косцов, если
известно, что в течение следующего дня
оставшуюся часть работы выполнил один косец?”
Решение.
На первом лугу косцы проработали  дня — вся бригада и дня — вся бригада и  дня — половина
бригады, что дня — половина
бригады, что  составляет
рабочего дня. На втором лугу в первый день
работала составляет
рабочего дня. На втором лугу в первый день
работала  бригады в течение
бригады в течение  дня, т. е. затрачено дня, т. е. затрачено  рабочего дня целой бригады.
Так как по площади второй луг в 2 раза меньше
первого, то, для того чтобы выкосить его, вся
бригада должна была бы работать рабочего дня целой бригады.
Так как по площади второй луг в 2 раза меньше
первого, то, для того чтобы выкосить его, вся
бригада должна была бы работать  дня. Следовательно, на
второй день на меньшем лугу останется дня. Следовательно, на
второй день на меньшем лугу останется  часть работы
всей бригады за день. А так как эту работу
выполнил один косец, значит вся бригада состояла
из 8 косцов. часть работы
всей бригады за день. А так как эту работу
выполнил один косец, значит вся бригада состояла
из 8 косцов.
Задача 4.
Эпитафия Диофанта.
На памятнике Диофанта находится следующая
надпись: “Прохожий ! Под сим камнем покоится прах
Диофанта,умершего в старости. Шестую часть его
жизни заняло
детство,двенадцатую-отрочество,седьмую-юность.
Затем протекла половина его жизни, после чего он
женился. Через 5 лет у него родился сын, а когда
сыну минуло 4 года, Диофант скончался. Скажи,
скольких лет он умер”.
Решение.
Часть жизни Диофанта ,протекшая от его рождения
до женитьбы, выразится суммой дробей:  часть его жизни
от женитьбы до смерти выразится разностью часть его жизни
от женитьбы до смерти выразится разностью 
Эта часть,очевидно, равна 5+4=9 годам. Значит,
Диофант умер,когда ему было  года. года.
Задача 5.
Древнеримская задача.
Один господин завещал капитал в 14 000 рублей
своей жене при условии, что если у неё родится
мальчик, то сын должен получить вдвое больше
матери, а если родится дочь, то мать должна
получить вдвое больше дочери. Родились близнецы:
сын и дочь. Как было исполнено завещание?
Решение.
Из наследства должна быть выделена одна часть
матери, две такие же части сыну, а половина такой
же части дочери. Все наследство должно быть
разделено на  части. Одна часть составляет
части. Одна часть составляет  рублей. Следовательно, мать
должна получить 4000 рублей, сын 8000 рублей, дочь 2000
рублей. рублей. Следовательно, мать
должна получить 4000 рублей, сын 8000 рублей, дочь 2000
рублей.
Задачи Древнего Востока.
Задача 6.
Некий математик насчитал на выгоне 70 коров.
“Какую долю от всего стада составляют эти
коровы?” - спросил математик у пастуха. “Я выгнал
пастись две трети от трети всего стада”, -
отвечал пастух. Сколько голов скота
насчитывается во всем стаде?
Решение.
Пусть Х — число голов скота во всем стаде.
Тогда:
Ответ: во всем стаде было 312 голов скота.

Задача 7.
Араб, чувствуя близкую кончину, призвал трех
сыновей своих и сказал им: “Когда я умру,
разделите между собой мое стадо верблюдов. Пусть
каждый из вас возьмет 1/2 всего стада, средний — 1/4,
а младший — 1/5”. Когда араб умер, сыновья хотели
разделить стадо, как завещал отец, но у них ничего
не вышло, так как в отцовском стаде оказалось 19
верблюдов. На их счастье мимо проходил мулла,
слывший за умного человека. Узнав в чем дело, он
предложил сыновьям занять у соседа одного
верблюда, когда этот верблюд был приведен, его
присоединили к отцовскому стаду, затем мулла
приказал старшему взять половину стада, т. е. 10
верблюдов, среднему - 1/4 часть ,т. е. 5 верблюдов, а
младшему 1/5 часть ,т. е. 4 верблюда.
“Сколько верблюдов вы разобрали?” - спросил
мула. Братья сосчитали и ответили: “19”. “Но
оставшегося верблюда верните соседу”, - сказал
мулла. Все ли участники дележа рассуждали
правильно, и не заблуждался ли кто-нибудь из них?
Решение.
Заблуждался сам завещатель: отказывая в своем
завещании сыновьям 1/2,1/4 и 1/5 всего стада, он
упустил из виду, что эти доли всего стада не
составляют в сумме единицу, т. е. Всего стада.

Не хватает 1/20. Это и понял мулла и приказал
добавить к стаду одного верблюда, т. е.
недостающую часть стада.
4. Итог урока.
Ребята, что нового вы открыли для себя на уроке?
Какая задача вам больше всего понравилась?
Почему?
5. Домашнее задание.
Древнегреческая задача о статуе Минервы
(богини мудрости, покровительнице , наук,
искусств и ремесел).
Я изваяние из злата, поэты то злато в дар
принесли.
Хоризий принес половину сей жертвы.
Фестия часть восьмую дала, десятую — Солон.
Часть двадцатая — жертва певца Фемисона.
А девять — все завершивших талантов —
Обет, Аристоником данный.
Сколько же злата поэты все вместе в дар принесли?
Решение.
Пусть поэтами в дар принесены Х талантов.
Уравнение выглядит так:
Ответ: 40.

xn--i1abbnckbmcl9fb.xn--p1ai
|
