Сайт учителя математики Сабениной Ирины Александровны. Математика древней руси
§ 20. Древнерусская математика ВIX в. образовалась Киевская Русь – государство, объединившее племена славян. Несколько раньше на территории , занятой этими племенами, складывается феодальный строй. В 988 г. при князе Владимире Киевская Русь приняла от Византии христианство. После крещения на Русь из Византии стали проникать культура и просвещение. Нумерация и письменность, первоначально составленные в IX в. по образцу греческой для Болгарии, позднее были перенесены без существенных изменений в Киевскую Русь. Нумерация была алфавитной, т.е. для обозначения узловых чисел: единиц, десятков и сотен использовались последовательные буквы алфавита – тип, скопированный с древнегреческой нумерации. Для отличения цифр от букв над буквой писали специальный знак , который назывался «титло». Приведем примеры записи чисел по этой старославянской системе (рис. 32).  рис.32 Имелись и обозначения для гораздо больших степеней 10, хотя это и не вызывалось практической необходимостью (на Руси было пристрастие к большим числам). Вот пример записи промежуточного числа: Следовательно, эта нумерация, как и любая алфавитная, была аддитивной, а кроме того, десятичной непозиционной. Действия над натуральными числами производились, видимо с помощью перекладывания костей или камешков. Из дробей были известны  , а также половины этих долей, символических обозначений дробей не было. , а также половины этих долей, символических обозначений дробей не было. Математические расчеты упоминаются в некоторых литературных сочинениях того времени, особенно в «Русской правде» - юридическом сборнике, впервые появившемся в XI в. и затем неоднократно видоизменявшемся и дополнявшемся. В частности, в этом сборнике выполняются денежные расчеты, связанные с торговлей и налогами, имеются сельскохозяйственные статьи на приплод скота, на подсчет урожая, на межевание земли и др. В IX- XI вв. феодальные отношения в Киевской Руси получают дальнейшее развитие. Киев и Новгород ведут оживленную торговлю с соседними странами и становятся крупными торгово-ремесленными центрами. Киевская Русь в XII в. – одно из наиболее развитых в экономическом и культурном отношении европейских государств. Но уже в XI в. начинается дробление древнерусского государства. В 1237-1242 гг. на Русь нагрянули отряды татаро-монголов и стали громить славянские княжества поодиночке; князья даже не пытались придти на помощь друг другу. От нашествия убереглось только Новгородское княжество, но и оно вынуждено было платить дань татарам; в настоящее время археологические раскопки именно в Новгороде дают ученым наибольшее количество открытий, относящихся к X-XIV вв., в виде записей на бересте. Славянам в крайне тяжелых условиях татаромонгольского ига приходилось думать не о торговле, а о том, чтобы выжить. Начиная с XIV в. Московское княжество занялось объединением славянских земель. Но окончательное избавление от ига татаро-монголов произошло лишь в 1480 г. при Иване III. В XV-XVII вв. складывается огромное многонациональное Российское государство. Математика требуется для многих целей: нужно было развивать торговлю, строит здания и крепости, измерять расстояния, площади и объемы, собирать налоги, составлять календарь. При этом школ не было, обучение письму, чтению и счету проводилось при монастырях, причем число обучающихся было весьма незначительным. Россия в XV-XVII вв. продолжала пользоваться старославянской нумерацией. В XV-XVII вв. складывается система мер. конечно, меры существовали еще в Киевской Руси и даже раньше, но, например, в различных княжествах Киевской Руси применялись разные меры, а нередко меры с одним и тем же названием отличались друг от друга. 1.Меры длины В XI-XII вв. имелись следующие единицы длины: пядь, локоть, сажень, верста. Существовали два вида пядей: малая пядь – расстояние между концами большого и указательного пальцев руки, расставленных в стороны (около 19 см), и большая пядь – расстояние между концами большого пальца и мизинца (около 23 см). Локтем называлось расстояние от конца вытянутого среднего пальца до локтевого сгиба (около 46 см). В XV-XVII вв. эти единицы сохраняются. Имелось несколько видов саженей, как и в Киевской Руси, но главной становится косая сажень - расстояние от концов пальцев вытянутой в верх правой руки до концов пальцев левой ноги (около 213 см). Верста определялась как 500 сажен (≈500∙2,13м=1,065 км). Вводились и такие единицы: аршин  сажени (около 71 см) и вершок сажени (около 71 см) и вершок аршина (≈4,4 см). аршина (≈4,4 см). Эти единицы были установлены как единая система мер России в XVII в., а окончательно уточнены указом Петра I в начале XVIII в. В указе были также установлены соотношения между этими единицами и английскими милями, футами и дюймами. 2.Меры площади Основными единицами площади с XVI в. становятся квадратная сажень и десятина  квадратных сажен (≈1,1 га). квадратных сажен (≈1,1 га). 3.Денежные единицы. В Киевской Руси основной денежной единицей была гривна - брусок серебра (весом около 409 г.). В XII-XIII вв. гривну стали рубить на две равные части; одна такая часть стала называться рублем. Настоящий денежный счет начинается в XV в. С XVI в. употребляются следующие денежные единицы: 1 рубль = 100 копейкам, 1 полтина = 50 копейкам, 1 гривенник = 10 копейкам, 1 алтын = 3 копейкам, деньга = ½ копейки, 1 полушка = ½ деньги.
Меры веса
Киевская гривна с XVI в. стала называться фунтом и превратилась в весовую единицу. Фунт позднее стал определяться так: это вес «доброй» горсти зерна, которую может удержать на ладони человек. Пуд, который долгое время определялся по- разному, с XVI в. стал приравниваться 40 фунтам (≈40∙409 г≈16,4 кг). Подсчеты велись на счетной доске. К XVIII в. она трансформировалась в русские счеты. В XVI и особенно в XVII в. появляются в значительном количестве русские математические рукописи, как правило, безымянных авторов. Эти рукописи были, в основном, оригинальны, а не являлись переводами или переработками сочинений зарубежных математиков. Из их содержания видно, что они предназначались для купцов, чиновников, землемеров и др. Рукописи строились по одному и тому же плану. Сначала рассматриваются натуральные числа (старославянская нумерация) и дроби, а также правила арифметических действий над ними. Затем следуют задачи, главным образом, прикладного характера, разделенные на типы: «Статья тройная» (тройное правило), «Статья деловая» (пропорциональное деление), «Статья торговая», «Дощаной счет», «Меновая в торгах», «Складная торговля» и др. В рукописях приводятся и европейские цифры (в десятичной позиционной нумерации), правда, довольно редко. Встречались также отдельные рукописи по геометрии, например, содержательный учебник Елизарьева (многие теоремы планиметрии, главным образом, из «Начал» Евклида, без доказательств). С появлением в России книгопечатания издаются не только книги религиозного характера, как было до XVII в., но и книги светского содержания, в том числе отдельные книги по математике. Появляются и переводные сочинения по математике. Все же в конце XVII в. Россия далеко отставала по уровню развития экономики, культуры и науки от передовых стран Западной Европы: Англии, Голландии и др. Крупный подъем страны наступает в первой четверти XVIII в. в связи с реформаторской, преобразовательной деятельностью Петра I . studfiles.net Математика в Древней Руси - Рефераты для всехОпубликовано 18.04.2013 21:58  Предки русского народа — славяне — с незапамятных времён жили на землях Средней и Восточной Европы. Первые письменные упоминания о славянах встречаются в книгах древних римлян, написанных в самом начале нашей эры. Арабские книги говорят о том; что в середине первого тысячелетия славяне вели большую торговлю с греками, арабами и другими народами и храбро воевали с иноземцами, которые пытались их покорить. В X веке нашего летосчисления у славян появилась письменность. С этого времени начинается «писаная» история Древней Руси. Предки русского народа — славяне — с незапамятных времён жили на землях Средней и Восточной Европы. Первые письменные упоминания о славянах встречаются в книгах древних римлян, написанных в самом начале нашей эры. Арабские книги говорят о том; что в середине первого тысячелетия славяне вели большую торговлю с греками, арабами и другими народами и храбро воевали с иноземцами, которые пытались их покорить. В X веке нашего летосчисления у славян появилась письменность. С этого времени начинается «писаная» история Древней Руси.
У славян, как и у всех других народов, первым учителем математики была жизнь, практика. Постепенно рождались и накапливались навыки счёта, правила измерения: ведь без этого нельзя было бы ни торговать, ни даже обмениваться продуктами. В первом тысячелетии у славян появилась денежная единица — рубль, название которой сохранилось до наших дней. Слово «рубль» происходит от глагола «рубить». Первые рубли, по всей вероятности, были просто кусочками металла, которые отрубали от полосы серебра или меди. Для того чтобы разрубить металлическую полосу на равные части, нужно было знать простейшие дроби, уметь складывать и вычитать числа. При измерении полей славяне употребляли и более сложные дроби. В раскопках славянских селений учёные находили изображения циркуля. Значит, древним славянам были известны некоторые свойства окружности. Основу своего алфавита славяне вместе с христианской религией позаимствовали от средневековых греков — византийцев. Способ записи цифр буквами со специальными значками —- «титлами» — они тоже взяли от греков (см. рисунок 1) . Крупные числа записывали с помощью специальных знаков, в названиях некоторых из них также видно византийское начало (см. рисунок 2) . С появлением письменности в Древней Руси стали появляться переводы греческих книг. Поначалу это были только «священные» книги, но и в них нет-нет да и встречались обрывки замечательной математики древних греков. Знания славян по математике постепенно росли. Известно, что в Англии в VII веке чудом учёности считался монах, который умел выполнять деление чисел: долго считалось, что нет ничего труднее четырёх действий арифметики над целыми числами. По-видимому, математические знания наших предков славян около 1000 года были не ниже, чем у западных народов. Однако в XIII веке большая часть русских княжеств была захвачена ордами полудиких кочевников — монголов. Жизнь замерла; приостановилось и развитие древнерусской культуры. Почти триста лет длилось монгольское иго. За это время наука Западной Европы сделала большой шаг вперёд: народы Европы ознакомились с замечательной математикой арабов и индийцев. А в отрезанной от всего культурного мира России математика стала отставать от науки Западной Европы. Для того чтобы потом, после свержения монгольского ига, снова выйти в ряды мировой науки, ей понадобилось несколько столетий. В XVI веке при Иване Грозном на Руси появляются первые рукописные учебники по математике, а немного позже — печатные книги о применении математики для разных практических нужд, например «Книге сошного письма» и «Устав ратных, пушечных и иных дел, касающихся до воинской науки». В 1134 году новгородский монах Кирик написал сочинение «. о том, как узнать человеку числа всех лет». Это самый древний дошедший до нас письменный памятник славянской математики. В своей рукописи Кирик подробно вычисляет, сколько лет, месяцев, недель и дней прошло от «сотворения мира» до года, в котором он, Кирик, писал свой труд. Главная «священная» книга христиан — Библия — дала церковникам основание утверждать, что мир был сотворён богом ровно за 5508 лет до начала нашего летосчисления. Кирик, по-видимому, где-то ошибся: число месяцев у него получилось больше, чем должно быть, но это, конечно, никому не повредило. Ведь вычисления Кирика никому, кроме него самого, не были нужны; они не могли принести никакой практической пользы людям. Видимо, Кирик был «числолюбцем», ему доставлял удовольствие сам процесс вычисления. А вот для нас рукопись Кирика очень важна. Она ясно показывает, что славяне без малого тысячу лет назад отлично владели четырьмя действиями арифметики, свободно обращались с очень большими целыми числами и с очень маленькими дробями. Что усвоение всего этого представляло большие трудности, доказывает хотя бы то, что в немецком языке есть поговорка: «Попал в дроби». Так говорят про человека, который оказался в трудном положении, или, по-нашему, «попал в переплёт». Ещё в XVIII веке в одном английском учебнике арифметики было написано, что дроби приводят учащихся в уныние и к мысли: «В эти дебри мы не пойдём!». Выходит, что в это время на Руси математика не только не отставала, но, пожалуй, шла даже немного впереди науки народов Западной Европы. Трудно переоценить и значение рукописного труда, который, по мнению исследователей, можно назвать первым учебником геометрии - «Синодальная № 42» (см. рисунок 3) . Составителем рукописи, которая датируется 1625 годом, был Ивашка Елизарьев. “Сие предисловие собрал я, Ивашко, князь Елизарьев сын. от многих учителей и их книги у меня все”. В этом первом учебнике геометрии содержались не только способы решения задач, но и давались основы теоретических знаний по геометрии. Рукопись была богато иллюстрирована картинками, гравюрами, при этом, последние были вырезаны из неизвестной современникам книги по геометрии. В 1682 году в Москве вышла книга: «Считание удобное, которым всякий человек, купующий и продающий, зело удобно изыскати может число всякой вещи». Это была первая в России не рукописная, а напечатанная в типографии книга по математике, которая должна была помогать решению разных практических задач. Была в ней таблица умножения (до 100х100), записанная славянскими цифрами. Особенно важную роль в развитии русской науки сыграла книга «Арифметика, или наука числительная», написанная Леонтием Филипповичем Магницким (см. рисунок 4) . «Арифметика» Магницкого была издана при Петре I, в 1703 году и долгое время была настольной книгой всех образованных русских людей. Великий русский ученый Михаил Васильевич Ломоносов знал её наизусть и называл её вместе с учебником грамматики «вратами своей учености». Книга Магницкого называлась «Арифметика», но кроме арифметики там были начала алгебры, геометрии, тригонометрии и даже немного мореходной астрономии. Это была настоящая энциклопедия по математике, в которой каждое правило, каждый приём подробно разъяснялся и подкреплялся решением примеров и практических задач. Замечательной книгой Магницкого закончилась многовековая история древнерусской математики. Дальнейшее развитие отечественной математики происходило в тесной связи с наукой Западной Европы, а многие видные европейские ученые даже работали в России. Но это уже совершенно другая страница истории, узнать о которой Вы можете, прочитав «Развитие математики в России в середине XVIII века». referat-4all.ru Математика в Древней Руси. Математика в Древней Руси. Собственно принято называть Древней Русью период истории с 10 по 17 век. Древняя Русь с принятием крещения в 988 г приняла письменность и научные знания из Византии – Восточной Римской империи, основанной Константином Великим. Господство религии было определяющим в научном мировоззрении. Математика в понятиях Древней Руси воспринималась с позиции Иоанна Дамаскина, византийского монаха, описавшего философскую систему в трактате «Источник знания». «Разделяет же ся философия в зрительное и деятельное». «Зрительная философия» - теоретическое знание, которое в свою очередь делится на богословие (наука о богопознании), естествознание и математику. Математика объединяла в себе арифметику, геометрию, астрономию и музыку. Первый труд по арифметике был написан в 1136 году Кириком Новгородцем. Его наименование было пространным: «Учение, им же ведати человеку числа всех лет». Он представлял собой средневековый научный трактат, где переплетались математические, календарные, хронологические и философские идеи и представления. Основные приложения математика имела к хронологии. Как известно, все летописные своды ведут отчет от «сотворения мира», т.е. византийские хронологии, берущие основания из текстов Библии, преимущественно Септуагинты (перевода 70 толковников в 3 веке до нашей эры по приказу царя Птолемея для Александрийской библиотеки). Основным идеологом этой системы считают Иоанна Дамаскина и Ефрема Сирина. Основные идеи византийской хронологии: 1. Неделя творения включена как обычная неделя из 6 дней. То есть появление звезд, солнца и луны было в среду, а появление человека в пятницу, так как первым днем творения считалось воскресенье. Начало новой эры приходится на 5508 г, таким образом сейчас идет 7523 год с 14 сентября 2015 г. 2. Основная задача хронологии древности – это расчет празднования Пасхи. В 325 г был созван по повелению Константина Великого 1 Вселенский собор, на котором епископы договорились праздновать Пасху в первое воскресение после первого весеннего полнолуния, сразу же после еврейской Пасхи, но не раньше нее. (После 21 марта по юлианскому стилю). 3. Средневековые астрономы установили следующие факты из движения солнца, луны и земли: Все фазы луны повторяются через каждые 19 лет – лунный круг, а взаимные положения солнца и земли через каждые 28 лет – солнечный круг. Если перемножить 19 и 28 то получим 532 года – период, через который Пасха приходится на одно и тоже календарное число по юлианскому стилю. Данный период назван – Великий индиктион. Монахи составляли специальные таблицы – пасхалии, очень громоздкие и неудобные в употреблении. Обычно их печатали в Типиконе – книге, содержащей устав православной церкви. В последствии данные таблицы заменил на формулы великий математик Карл Гаусс. Вычислим Пасху в 2016 году. Найдем остатки от деления R (число года) на 19, 4 и 7.
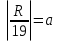 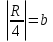 
2. Вычислим d и e 
Если 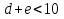 , то искомая дата , то искомая дата 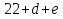 – марта, – марта, 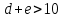 , то искомая дата , то искомая дата 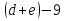 апреля по юлианскому стилю. Напоминаем, что разница между стилями 13 дней. апреля по юлианскому стилю. Напоминаем, что разница между стилями 13 дней. Для 2016 года имеем: 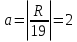  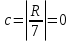
 , , 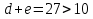
Пасха приходится на 27 – 9 = 18 апреля или (18+13=31) 1 мая по новому стилю. Узнаем, в какой день недели было 22 июня 1941 года. R = 1941 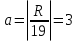  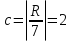
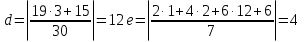 , , 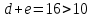
Пасха приходится на 16 – 9 = 7 апреля или (7+13=20) апреля по новому стилю. 22 июня это: 10+31+22 = 63 день после Пасхи. Дни недели распределены следующим образом. Остаток при делении на 7 0 1 2 3 4 5 6 День недели. воскресение понедельник вторник среда четверг пятница суббота 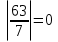 . Значит 22 июня 1941 года было воскресение. (Неделя всех русских святых). . Значит 22 июня 1941 года было воскресение. (Неделя всех русских святых).
infourok.ru "Задачи Древней Руси". 5–6-е классы  Разделы: Математика Цели урока:
- Знакомство с историей математики.
- Формирование и развитие интереса к математике.
- Активизация познавательной деятельности
учащихся.
Слава нашей стороне!
Слава нашей старине!
Колесо истории мы повернем
И рассказывать начнем,
Чтобы все вы знать могли
О делах родной земли.
Страница первая
Славяне.
Предки русского народа – славяне – с
незапамятных времен жили на землях Средней и
Восточной Европы. Первые письменные упоминания о
славянах встречаются в книгах древних римлян,
написанных в самом начале нашей эры. Арабские
книги говорят о том, что в середине первого
тысячелетия славяне вели большую торговлю с
греками, арабами и другими народами и храбро
воевали с иноземцами, которые пытались их
покорить. В Х веке нашей эры у славян появилась
письменность. С этого времени начинается
“писаная” история Древней Руси.
Первые сведения о развитии математики на Руси
относятся к IX-XII вв. (древнерусская нумерация,
метрология, первые системы дробей и др.). В
Древней Руси времен Ярослава Мудрого (978-1054) уже
существовали общеобразовательные школы
древнерусского права “Русская правда” и в
памятниках духовного содержания: “Книга святых
тайн Еноха”, “Шестоднев”, “Толковая палея” и
др.
Феодальная раздробленность и иноземное
нашествие сыграли роковую роль в исторической
судьбе, и надолго задержали культурное и научное
развитие Киевской и Новгородской Руси. Поэтому
вновь математика начинает развиваться на Руси
только в XVI в. после освобождения от татарского
ига. В первых рукописях создается создается
самобытная русская математическая терминология.
Сохранилась рукопись XVI в. “Книга сошному
письму”, содержащая “статью”, посвященную
вычислению налога с земельной площади в
“сохах”. Для расчетов “сошного письма”
применялись русские счеты. Арифметические
рукописи XVI в. переписывались и в XVII в. и имели
традиционное название “Книга рекома по-гречески
арифметика, а по-немецки – алгоризма, а по-русски
цифирная счетная мудрость”.
Задание.
Решить задачу с помощью счет.
Шли 7 старцев.
У каждого старца по 7 костылей,
На каждом костыле по 7 сучков,
На каждом сучке по 7 кошелей,
В каждом кошеле по 7 пирогов,
В каждом пироге по 7 воробьев.
Сколько всего?
Решение.
7+72+73+74+75+76=7+49+343+2401+16807+117649=137256
Ответ: 137256.
Страница вторая.
Славянские цифровые знаки.
У славян, как и у всех других народов, первым
учителем математики была сама жизнь, практика.
По-видимому, все народы вначале обозначали числа
зарубками на палочках, которые у русских
назывались бирками. Такой способ записей
долговых обязательств или налогов применялся
малограмотными людьми разных стран.
Легко понять происхождение названий чисел:
одиннадцать = один-на-десять, двенадцать =
два-на-десять и так далее, двадцать = двадесять,
тридцать = тидесять и так далее.
Способ записи цифр буквами со специальными
значками-“титлами” - они тоже взяли от греков. В
хозяйственной жизни далекого прошлого люди
обходились сравнительно небольшими числами –
так называемым малым счетом наших предков. Он
доходил до числа 10000, которое в самых старых
памятниках называется “тьма”, то есть темное
число, которое нельзя ясно представить.
В дальнейшем граница малого счета была
отодвинута до 108, до числа “тьма тем”.
Старинная рукопись по этому случаю заявляет, что
“больше сего числа несть человеческому разуму
разумети”.
Задание.
Задача из “Счетной мудрости”
Идет корабль по морю, на нем мужеска полу и
женска 120 человек. Найму дали 120 гривен, мущины
дали по 4 алтына, а женщины дали по 3 алтына с
человека. Сколько мужеска полу было и женска
порознь? (Гривна, гривенник – десять копеек,
алтын равнялся трем копейкам).
Решение.
(1200-120*9):(12-9)=40 мужчин
120-40=80 женщин
Ответ: 40 мужчин, 80 женщин.
Страница третья.
“Учение им же ведати человеку числа
всех лет”.
Еще в раннюю эпоху Русского государства
находились среди народа “числолюбцы”, которые
интересовались математикой не только потому, что
она нужна в практической жизни. Их влекло и чисто
исследовательское любопытство.
В 1134 году новгородский монах Кирик написал
сочинение “…о том, как узнать человеку числа
всех лет”. Это самый древний дошедший до нас
письменный памятник славянской математики. В
своей рукописи Кирик подробно вычисляет, сколько
лет, месяцев, недель и дней прошло от сотворения
мира до года, в котором он, Кирик, писал свой труд.
Главная священная книга христиан – Библия –
дала церковным историкам основания утверждать,
что мир был сотворен Богом ровно за 5508 лет до
начала нашего летосчисления. Кирик, по-видимому,
где-то ошибся: число месяцев у него получилось
больше, чем должно быть, но это, конечно, никому не
повредило. Ведь вычисления Кирика никому, кроме
него самого, не были нужны; они не могли принести
никакой практической пользы людям. Видимо, Кирик
был “числолюбцем”, ему доставлял удовольствие
сам процесс вычисления.
Задача Кирика Новгородца.
Сколько месяцев, недель, дней и часов прожил
человек, которому в 1136 г. Исполнилось 26 лет?
Решение.
12*16=312 месяцев
365*26+7=9497 дней
9497:7=1356 недель
24*9497=227928 часов.
Заключение.
О, Русь – великий звездочет!
Как звезд не свергнуть с высоты,
Так век неслышно протечет,
Не тронув этой красоты.
Как будто древний этот вид
Раз навсегда запечатлен
В душе, которая хранит
Всю красоту былых времен…
Поделиться страницей: xn--i1abbnckbmcl9fb.xn--p1ai проект.docx - проект "Математика Древней Руси" дворнике Герасиме, что он был «мужчина двенадцати вершков роста», а у Ф.М. Достоевского в «Идиоте» сопровождает Рогожина «какойто огромный, вершков двенадцати господин», ведь вершок – это всегото чуть более четырех сантиметров?Денежные единицы на Руси В связи с развитием земледелия, товарообмена, а затем ремесел и торговли у славян появились и постепенно совершенствовались единицы для измерениядлин, площадей, сыпучих тел, денег и пр. Однако эти меры не были устойчивы: их значение с течением времени иногда изменялось. Денежными знаками у славян служили сначала домашние животные и их шкуры. В это время денежные единицы носили соответствующие наименования: "куны" (от слова куница), "резаны" (шкуры, нарезанные на куски) и "ногаты" . С переходом к металлическим деньгам между прежней и новой системой единицустановилось соответствие. Металлическая (серебряная) гривна приравнивалась к 20 ногатам, 25 кунами 50 резанам. Русская серебряная гривна была, очевидно, заимствована у арабов, так как она в весовых единицах была равна арабской единице "ротль". В более поздние времена (XIVXV вв.) основной денежной единицей стал "рубель" или "рубль", представлявший собой отрубленный кусок серебра весом около 205 г. В эту эпоху в ходу были * "полтина" (1/2 рубля), * "гривна" (1/10 рубля) * "деньга" (1/100 рубля). Позднее появилась "копейка", на которой изображался всадник с копьем, откуда, как полагают, и произошло это название. Стоимость деньги составляла 1/2 копейки, и со временем деньгу стали называть полушкой, а иногда грошем. Кроме указанных денежных единиц, существовал "алтын", заимствованный от татар ("алты" потатарски означает шесть), равный стоимости 6 денег или 3копеек. Некоторое время (при Иване III и Василии III) имели распространение "саблянки", получившие свое наименование от изображенного на них воина с саблей и равнявшиеся по стоимости одной деньге. Меры длины на Руси Для измерения длины употреблялись меры, большей частью связанные с znanio.ru Сайт учителя математики Сабениной Ирины| Календарь | « Июль 2018 » | | Пн | Вт | Ср | Чт | Пт | Сб | Вс | | | | | | | | 1 | | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | 16 | 17 | 18 | 19 | 20 | 21 | 22 | | 23 | 24 | 25 | 26 | 27 | 28 | 29 | | 30 | 31 |
 Архив записей | Математика в древней РусиПредки русского народа – славяне – с незапамятных времен жили на землях Средней и Восточной Европы. Первые письменные упоминания о славянах встречаются в книгах древних римлян, написанных в самом начале нашей эры. Арабские книги говорят о том, что в середине первого тысячелетия славяне вели большую торговлю с греками, арабами и другими народами и храбро воевали с иноземцами, которые пытались их покорить. В Х веке нашей эры у славян появилась письменность. С этого времени начинается "писаная” история Древней Руси.У славян, как и у всех других народов, первым учителем математики была жизнь, практика. Постепенно рождались и накапливались навыки счёта, правила измерения: ведь без этого нельзя было бы ни торговать,ни даже обмениваться продуктами.В первом тысячелетии у славян появилась денежная единица — рубль,название которой сохранилось до наших дней. Слово «рубль» происходит от глагола «рубить». Первые рубли,по всей вероятности, были просто кусочками металла, которые отруба-ли от полосы серебра или меди. Для того чтобы разрубить металлическую полосу на равные части, нужно было знать простейшие дроби:½ ¼,уметь складывать и вычитать числа.При измерении полей славяне употребляли и более сложные дроби: ¹⁄₆, ¹⁄₈. В раскопках славянских селений учёные находили изображения циркуля. Значит, древним славянам были известны некоторые свойства окружности. Основу своего алфавита славяне вместе с христианской религией позаимствовали от средневековых греков — византийцев. Способ записи цифр буквами со специальными значками — «титлами» — они тоже взяли от греков. С появлением письменности на Древней Руси стали появляться переводы греческих книг.Поначалу это были только «священные» книги, но и в них нет-нет да и встречались обрывки замечательной математики древних греков. Знания славян по математике постепенно росли.Известно, что в Англии в VII веке чудом учёности считался монах,который мог выполнить деление чидиких кочевников — монголов. Стон стоял над Русской землёй. Горели го-рода, лилась кровь. Жизнь замерла;приостановилась и древнерусская образованность.Почти триста лет длилось монгольское иго. За это время наука Западной Европы сделала большой шаг вперёд: народы Европы ознакомились с замечательной математикой арабов и индийцев. А в задавленной захватчиками и отрезанной от всего культурного мира России математика стала отставать от науки Западной Европы.Для того чтобы потом, после свержения монгольского ига, снова выйти в ряды мировой науки, ей понадобилось несколько столетий.В XVI веке, при Иоанне Грозном, на Руси появляются первые рукописные учебники по математике, а немного позже — печатные книги о применении математики для разных практических нужд; таковы, например, «Книга сошного письма» и «Устав ратных, пушечных и иных дел, касающихся до воинской науки». ( ( ) ) | Новости сайта полезные сайты | | | |
sabeninairina10.ucoz.ru Математика Древней Руси — реферат Пример: запишем число 365 на абаке и удвоим его. Абак состоял из вертикальных колонок, в которых камешками и другими мелкими предметами можно было в нечетных колонках выразить единицы разрядов: от 1 до 4, а в четных – одним счетным предметом сразу пять разрядов. В первой колонке нет косточек, во второй – положена одна косточка, что обозначает число 5. В третьей колонке лежит одна косточка, она обозначает один десяток; в четвертой также одна косточка, но она выражает сразу пять десятков, поскольку четвертая колонка – четная. Значит, этими двумя косточками в третьей и четвертой колонках обозначается число 60. В пятой колонке указаны три косточки, каждая из которых выражает 100, т.е. вместе 300. Т.о. на модели шестью косточками обозначено число 365. Пусть требуется узнать, сколько будет стоить в гривнах 365 коров по цене в 2 гривны и 365 баранов по 10 резан. Отложим число а = 365 на абаке. И разделим колонки схемы поперечной чертой. Удвоенный результат 2а = 730 расположим в верхней части модели. Это стоимость коров в гривнах. Для определения стоимости баранов в гривнах необходимо кроме удвоения сместить разрядные значения влево на одну пару колонок. Тогда получится, что 365 баранов стоят 73 гривны. На этом примере видно, что вычисление стоимости коров по цене 2 гривны, отнесенное к 1-й группе сложности, и вычисление стоимости баранов по 10 рязан, отнесенное ко второй группе сложности, на модели абака выполняются аналогично: посредством операции удвоения. Разница состоит в различном прочтении результата. В первом случае результат читается в соответствии со способом записи числа а. Во втором случае разрядные значения смещаются на одну пару колонок: сотни читаются как десятки, а десятки как единицы. Модель абака Меры Древней Руси С древности, мерой длины и веса всегда был человек: на сколько он протянет руку, сколько сможет поднять на плечи и т.д. В Древней Руси была принята русская система мер (она использовалась до 1899 г.). Меры длины: 1 миля (старорусская) = 7 вёрст = 7,4676 км. 1 верста = 500 саженей = 1066,8 м. 1 сажень = 3 аршина = 7 футов = 12 пядей = 48 вершков = 84 дюйма = 100 соток = 2,1336 м. 1 аршин = 4 четверти = 28 дюймов = 16 вершков = 71,12 см. 1 фут = 12 дюймам = 304,8 мм. 1 четверть (пядь) = 1/12 сажени = 1/4 аршина = 4 вершка = 7 дюймов = 177,8 мм. 1 вершок = 1,75 дюйма = 44,45 мм. 1 дюйм = 10 линиям = 25,4 мм. 1 сотка = 1/100 сажени = 84 точкам = 21,336 мм. 1 линия = 10 точкам = 2,54 мм. 1 точка = 1/100 дюйма = 1/10 линии = 0,254 мм. Меры площади: 1 кв. верста = 250 000 кв. саженям = 1,1381 км². 1 десятина = 2400 кв. саженям = 10 925,4 м² = 1,0925 га. 1 четь = 1/2 десятины = 1200 кв. саженям = 5462,7 м² = 0,54627 га. 1 осьминник = 1/8 десятины = 300 кв. саженям = 1365,675 м² ≈ 0,137 га. 1 кв. сажень = 9 кв. аршинам = 49 кв. футам = 4,55225 м². 1 кв. аршин = 256 кв. вершкам = 0,505805 м². 1 кв. вершок = 19,758 см². 1 кв. фут = 144 кв. дюймам = 0,092903 м². 1 кв. дюйм = 100 кв. линиям = 0,00064516 м². Меры объема: 1 куб. сажень = 27 куб. аршинам = 343 куб. футам = 9,7127 м³ 1 куб. аршин = 4096 куб. вершкам = 21 952 куб. дюймам = 359,7288 дм³ 1 куб. вершок = 5,3594 куб. дюймам = 87,8244 см³ 1 куб. фут = 1728 куб. дюймам = 28,3168 дм³ 1 куб. дюйм = 1000 куб. линий = 16,3871 см³ 1 куб. линия = 1/1000 куб. дюйма = 16,3871 мм³ Меры сыпучих тел: 1 цебр = 26—30 четвертям. 1 кадка (кадь, оков) = 2 половникам = 4 четвертям = 8 осьминам = 839,69 л (= 14 пудам ржи = 229,32 кг). 1 куль: ржи — 9 пудов + 10 фунтов = 151,52 кг; овса — 6 пудов + 5 фунтов = 100,33 кг 1 полокова, половник = 419,84 л (= 7 пудам ржи = 114,66 кг). 1 четверть, четь (для сыпучих тел) = 2 осьминам (получетвертям) = 4 полуосьминам = 8 четверикам = 64 гарнцам. (= 209,912 л (дм³) 1902 г.). (= 209,66 л 1835 г.). 1 осьмина = 4 четверикам = 104,95 л (=1¾ пуда ржи = 28,665 кг). 1 полосьмины = 52,48 л. 1 четверик = 1 мере[3] = 1⁄8 четверти = 8 гарнцам = 26,2387 л. (= 26,239 дм³ (л) (1902 г.)). (= 64 фунтам воды = 26,208 л (1835 г)). 1 получетверик = 13,12 л. 1 четвёрка = 6,56 л. 1 гарнец, малый четверик = ¼ ведра = 1⁄8 четверика = 12 стаканам = 3,2798 л. (= 3,28 дм³ (л) (1902 г.)). (=3,276 л (1835 г.)). 1 полугарнец (пол-малый четверик) = 1 штоф = 6 стаканам = 1,64 л. (Пол-пол-малый четверик = 0,82 л, Пол-пол-пол-малый четверик = 0,41 л). 1 стакан = 0,273 л. Меры жидких тел: 1 бочка = 40 вёдрам = 491,976 л (491,96 л). 1 корчага = 2 ведра (около 25 л.). 1 ведро = 4 четвертям ведра = 10 штофам = 1/40 бочки = 12,29941 л (на 1902 г.). 1 четверть (ведра) = 1 гарнец = 2,5 штофа = 4 бутылкам для вина = 5 водочным бутылкам = 3,0748 л. 1 гарнец = 1/4 ведра = 12 стаканам. 1 штоф (кружка) = 3 фунтам чистой воды = 1/10 ведра = 2 водочным бутылкам = 10 чаркам = 20 шкаликам = 1,2299 л (1,2285 л). 1 винная бутылка = 1/16 ведра = 1/4 гарнца = 3 стаканам = 0,68; 0,77 л; 0,7687 л. 1 водочная (пивная) бутылка = 1/20 ведра = 5 чаркам = 0,615; 0,60 л. 1 бутылка = 3/40 ведра (Указ от 16 сентября 1744 года). 1 косушка = 1/40 ведра = 1/4 кружки = 1/4 штофа = 1/2 полуштофа = 1/2 водочной бутылки = 5 шкаликам = 0,307475 л. 1 стакан = 0,273 л. 1 четушка = 1/50 ведра = 245,98 мл. 1 чарка = 1/100 ведра = 2 шкаликам = 122,99 мл. 1 шкалик = 1/200 ведра = 61,5 мл. Меры веса: 1 ласт = 6 четвертям = 72 пудам = 1179,36 кг. 1 четверть вощаная = 12 пудам = 196,56 кг. 1 берковец = 10 пудам = 400 гривнам (большим гривенкам, фунтам) = 800 гривенкам = 163,8 кг. 1 контарь = 40,95 кг. 1 пуд = 40 большим гривенкам или 40 фунтам = 80 малым гривенкам = 16 безменам = 1280 лотам = 16,380496 кг. 1 полпуда = 8,19 кг. 1 батман = 10 фунтам = 4,095 кг. 1 безмен = 5 малым гривенкам = 1/16 пуда = 1,022 кг. 1 полубезмен = 0,511 кг. 1 большая гривенка, гривна, (позднее — фунт) = 1/40 пуда = 2 малым гривенкам = 4 полугривенкам = 32 лотам = 96 золотникам = 9216 долям = 409,5 г (11—15 вв.). 1 фунт = 0,4095124 кг (с 1899 года). 1 гривенка малая = 2 полугривенкам = 48 золотникам = 1200 почкам = 4800 пирогам = 204,8 г. 1 полугривенка = 102,4 г. Кирк Новгородец Кирик Новгородец (1110 – не ранее 1156/1158) – средневековый новгородский мыслитель, диакон и доместник Антипова монастыря в Новгороде, автор «Учения о числах» (1136), математик, церковный писатель, летописец,музыкант. Произведение Кирка начинается без авторского вступления. Материал разбит на небольшие разделы размером от 4 до 18 строк; они занумерованы, номера (в древнерусской нумерации) вынесены на поля листов. В первых пяти параграфах идет речь о том, сколько прошло времени в различных единицах от «сотворения мира». До момента написания трактата, а именно: 1) в годах, 2) в месяцах, 3) в неделях, 4) в днях, 5) в часах. Каждый параграф содержит цифровой материал, связанный с числом 6644, как количество лет, которое прошло за указанный период. Это число точно датирует написание первых пяти пунктов 1136 годом. Пятый параграф завершается сентенцией, смысл которой таков: «ведь понемногу создается город и делается большим, так и знание понемногу растет». В следующих пунктах говориться о теоретических основах календарных вычислений: об индикте, о солнечном и лунном «кругах», о тысячелетиях, о так называемых обновлениях неба, земли, моря, воды, о високосных годах, о «великом круге». В каждом параграфе материал так или иначе связан с датой 6644г. В идущих далее пунктах говориться о числе месяцев, недель и дней в году с учетов високосных дней. Здесь материал не связан с 6644 г. Затем говорится о количестве часов в году и дне. Следующие параграфы посвящены так называемым дробным делениям числа. Эти параграфы так же не связаны с датой 6644г. К последнему параграфу примыкает, не имея самостоятельного номер, заключительный текст, в котором автор трактата указывает свое имя, год написания сочинения, ряд хронологических сведений и биографических данных о себе. Таким образом, в этом «Учении» выделяются следующие разделы: - О единицах счета времени (§ 1 – 5)
- О теоретических основах календаря (§ 6 – 18)
- О дробных делениях числа (§ 19 – 27)
Заключительный текст (Заключение). Сочинение Кирка – особого характера по форме, назначению и предмету изложения. Более всего соответствует жанру современной научно-популярной литературы. Заключение Итог изложения данных об облике древнерусской арифметической культуры X – первой половины XIII вв. в рамках данного доклада сводится к следующему. Знания способов записи чисел в архаичной (кириллической) системе нумерации использовали многие слои общества: ремесленники, зодчие, переписчики книг, духовенство, чиновники, «профессиональные» вычислители и другие. Обучение цифровой символике велось параллельно с обучением письму, основными учебными пособиями служили особые «цифровые алфавиты», подобные буквенным. Формирование древнерусской происходило как смешение византийской нумерации с кириллическим письмом с сохранением близости к греческому оригиналу. Цифровой византийский «язык» на русской почве изменился, но не настолько, чтобы не была понятна греческая математическая «речь». Это было важно для обеспечения поступления и усвоения математической информации из Византии. На цифровом фундаменте основывались знания о производстве вычислительных операций с использованием наглядно-инструментального приспособления типа абака. Эти сведения были достоянием более узкого круга лиц – хронологов, чиновников административно-хозяйственного аппарата: волостей, тиунов и др. Можно представить себе в следующем виде древнерусского вычислителя за работой. Его инструментами были: маленький мешочек с вишневыми и сливовыми косточками, дощечка для писания по воску («цера») и «писало» - металлическая или костяная палочка, имевшая с одной стороны заострение, а с другой – лопаточку. На дальнейшее развитие математической культуры Древней Руси повлияло татаро-монгольское иго, которое отбросило славян на несколько столетий назад в развитии математической науки в частности. Почти триста лет длилось монгольское иго. За это время наука Западной Европы сделала большой шаг вперёд: народы Европы ознакомились с замечательной математикой арабов и индийцев. А в задавленной захватчиками и отрезанной от всего культурного мира России математика стала отставать от науки Западной Европы. Для того чтобы потом, после свержения монгольского ига, снова выйти в ряды мировой науки, ей понадобилось несколько столетий. В XVI веке, при Иоанне Грозном, на Руси появляются первые рукописные учебники по математике, а немного позже — печатные книги о применении математики для разных практических нужд; таковы, например, «Книга сошного письма» и «Устав ратных, пушечных и иных дел, касающихся до воинской науки». В 1682 году в Москве вышла книга: «Считание удобное, которым всякий человек, купующий и продающий, зело удобно изыскати может число всякия вещи». Это была первая в России не рукописная, а напечатанная в типографии книга по математике, которая должна была помогать решению разных практических задач. Была в ней таблица умножения (до 100×100), записанная славянскими цифрами. Особенно важную роль в развитии русской науки сыграла книга «Арифметика, или наука числительная», написанная Леонтием Филипповичем Магницким - hotcooltop.com. «Арифметика» Магницкого была издана при Петре I, в 1703 году, и долгое время была настольной книгой всех образованных русских людей. Великий русский учёный Михаил Васильевич Ломоносов знал её наизусть и называл её вместе с учебником грамматики «вратами своей учёности». Книга Магницкого называлась «Арифметика», но, кроме арифметики, там были начала алгебры, геометрии, тригонометрии и даже немного мореходной астрономии. Это была настоящая энциклопедия по математике, в которой каждое правило, каждый приём подробно разъяснялся и подкреплялся решением примеров и практических задач - hotcooltop.com. Замечательной книгой Магницкого закончилась многовековая история древнерусской математики. Список использованной литературы: - Р. А. Симонов – математическая мысль Древней Руси, М.: Наука, 1997г., 120с.
- http://hotcooltop.com/article210.html
- http://rus.ans4.com/27706153/kakaya-sistema-mer-byla-v-drevney-rusi/
referat911.ru
|
