Системы счисления с древних времён до наших дней. Древняя система счисления

Системы счисления с древних времён до наших дней

Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и не удивительно: более 10 тыс. лет прошло с тех пор, как люди всерьёз занялись земледелием, скотоводством и производством простейших товаров. Назвать же имя гения впервые задавшегося вопросом «сколько?», тем более невозможно.

В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счете возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытных людей. Например, в 1937 году в Моравии на месте одной из таких стоянок найдена волчья кость с 55 глубокими зарубками. Позже в других местах ученые находили столь же древние каменные предметы с точками и черточками, сгруппированными по 3 или по 5. Это были древнейшие системы записи чисел – системы счисления.

Системы счисления с древнейших времён до наших дней.

Древнейшая система записи чисел называется единичной, т. к. любое число в ней образуется путем повторения одного знака, символизирующего единицу. Группировки и вспомогательные значки используются лишь для облегчения восприятия больших чисел.

Единичная система счисления первобытных людей, рисовавших палочки на стенах пещеры или делавших зарубки на костях животных и ветках деревьев не забыта и в наши дни. Как узнать, на каком курсе учится курсант военного училища? Сосчитайте сколько полосок нашито на рукаве его мундира. О количестве самолетов противника, сбитых асом в воздушных боях, говорит число звездочек, нарисованных на фюзеляже его самолета.

Поштучно считать предметы удобно тогда, когда их не очень много. Пересчитывать же таким образом большие совокупности скучно и утомительно, поэтому возникла идея объединять единицы в группы.

Позже появилось много различных числовых систем, вот наиболее известные из них.

Около 3-2,5 тысяч лет до нашей эры древние египтяне придумали свою числовую систему. В ней ключевые числа: 1, 10, 100 и т. д. – изображались специальными значками-иероглифами. Египтяне высекали их на стенах погребальных камер, писали тростниковым пером на свитках папируса.

Среди множества иероглифических систем счисления, которые существовали в разные времена у разных народов, только одна используется до сих пор. Ее цифры знакомы всем, хотя им уже около 2,5 тысячелетий. Эти цифры встречаются на циферблатах часов, фронтонах старинных и современных зданий, памятниках, страницах книг. Ну конечно же, речь идет о римской системе счисления.

Как читать римские цифры? Одно из правил записи римских чисел гласит: «если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае меньшая цифра не может повторяться), то меньшая вычитается из большей».

В наши дни любую из римских цифр запрещается записывать в одном числе более трех раз подряд. В связи с этим выражение VIIII, XXXX и т. п. считаются некорректными. Однако древние римляне о подобном ограничении ничего не ведали, и число 1995 скорее всего записали бы так: MDCCCCLXXXXV.

Кроме египетской и римской к иероглифическим системам чисел относятся финикийская, пальмирская, критская, сирийская, греческая аттическая, или Геродианова (именно из сообщения грамматика Геродиана, жившего во 2-3 веках, западноевропейские историки впервые узнали о ее существовании). Известны также старокитайская, староиндийская, ацтекская иероглифические системы. В них, как в египетской и римской системах вводятся ключевые числа, для обозначения которых применяются специальные иероглифы. Все остальные числа образуются приписыванием с той или иной стороны ключевого числа других ключевых чисел, возможно с некоторыми повторениями.

Любопытно отметить, что у многих народов для обозначения числа 1 применялся один и тот же символ – вертикальная черточка. Это самое древнее число в истории человечества. Оно возникло из простой черты на земле, из зарубки на дереве или кости.

Наряду с иероглифическими в древности широко применялись системы, в которых числа изображались буквами алфавита. Именно такой была греческая алфавитная нумерация, получившая название ионической. Она сменила аттическую систему в 3 веке до н. э. вместе с христианством и письменностью эта нумерация пришла к славянам – сначала к южным, потом и к восточным.

Похожие системы счисления, в которых буквы алфавиты по совместительству «подрабатывали» цифрами, использовались в старину у арабов, евреев, грузин, армян.

Записи чисел в алфавитной нумерации получаются более короткими, чем в иероглифической. Но и у той и у другой системы представления чисел есть один весьма существенный недостаток: арифметические действия над такими числами – занятие весьма трудоемкое. Этого неудобства нет у позионных систем. Идея приписывать цифрам разные величины в зависимости от того, какую позицию они занимают в записи числа, впервые появилась в 3 тысячелетии до н. эй. в Месопотамии (Междуречье) у древнего талантливого народа – шумеры. От них она перешла к вавилонянам – новым хозяевам Междуречья, почему и вошла в историю как вавилонская система счисления.

Шестидесятеричная система широко применялась в астрономических расчетах вплоть до эпохи Возрождения.

Индейский народ майя, обитавший на территории Центральной Америки, в начале новой эры представлял числа примерно так, как и древние шумеры. Майя изобрели похожую числовую систему, но с другими основаниями – пятеричную-двадцатиричную.

Древнейшая известная запись в позиционной десятичной системе обнаружена в Индии и датируется 595 годом. Появление хорошо знакомого нам нуля было подготовлено системами счисления, издавна применявшимися не только в Индии, но и в Древнем Китае. В этих старинных системах для записи одинакового числа единиц, десятков, сотен или тысяч использовались одни и те же символы, но дополнительно помечалось, в каком разряде они стоят. Постепенно заметили, что даже если не указывать имена разрядов, то число все ровно можно прочитать, т. к. у каждого разряда есть свое «посадочное место» – позиция. А если позиция пустая, то ее нужно пометить специальным значком – нулем. В поздних вавилонских текстах стал появляться такой знак, однако в конце числа его никогда не ставили. Лишь в Индии в 9 веке нуль окончательно занял свое место в нумерации, которая распространилась затем по всему миру.

Индийская нумерация пришла сначала в арабские страны, а затем и в Западную Европу. О ней подробно рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания сколь угодно больших чисел, записанных в позиционной системе, сделали ее особенно популярной. А поскольку труд аль-Хорезми был написан на общем для мусульманского мира языке- арабском, то за индийской нумерацией в Европе закрепилось неправильное название – «арабская».

В десятичной системе всего 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Говорят также, что эти цифры представляют собой коэффициенты разложения заданного числа по степеням 10, а само число 10 называют основанием системы счисления. «Вес» цифры в десятичной записи числа определяется ее позицией: чем дальше отстоит данная позиция от крайнего правого разряда единиц, тем большую «солидность» и «вес» она имеет. Поэтому принятая система записи чисел называется десятичной позиционной системой счисления.

Позиционная система счисления, в которой в качестве базовых чисел выбираются степени числа 2, называется двоичной позиционной системой счисления. Чтобы различить числа, записанные в разных системах счисления, их заключают в скобки, а внизу справа указывают основание системы счисления. Например, запись (1100)2 означает то же самое число, что и запись (12)10. Поскольку все мы пользуемся десятичной системой счисления, то десятичное основание обычно не указывается: (1100)2=12.

Двоичная система счисления стала одним из истоков произошедшей в 20 веке грандиозной компьютерной революции. Технически две цифры воспроизвести просто: один – проходит ток в полупроводниковом элементе, ноль – ток не проходит. Состояния элемента «проходит ток» и «не проходит ток» могут сменять друг друга за очень короткие промежутки времени – миллионные доли секунды. Это позволяет производить арифметические действия над двоичными цифрами с неимоверной скоростью.

По сравнению с громоздкими таблицами умножения и сложения в десятичной системе, таблицы умножения и сложения двоичных чисел миниатюрны.

Операции простейшие, и компьютер выполняет их безупречно. Но иногда в машине происходит какой-нибудь сбой или программа-задание компьютеру на выполнение расчетов - содержит ошибку. Тогда программистам приходится перепроверять себя и компьютер, поэтому без знания всей компьютерной кухни, «стряпающей» двоичные числа, хорошему специалисту никак не обойтись.

К недостаткам двоичной системы можно отнести только «длинную» запись чисел (чем меньше в системе цифр, тем длинее будет запись числа). Перевод в двоичную систему вряд ли удастся выполнить в уме, поэтому стали использовать системы, родственные двоичной системе счисления, в которых запись числа на бумаге короче, чем в двоичной, а алгоритмы перевода не требуют сложных вычислений.

В восьмеричной системе 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, записанная в младшем разряде означает – как и в десятичном числе просто единицу, а в следующем разряде она означает 8, в следующем – 64 и т. д.

Запись числа в восьмеричной системе достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. Для первых десяти цифр используются привычные цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а для остальных шести цифр – первые буквы латинского алфавита: A-10, B-11, C-12, D-13, E-14, F-15. Как и в восьмеричной системе, цифра 1, записанная в младшем разряде, означает единицу. В следующем разряде та же цифра 1 означает 16, в следующем – 256 и т. д. цифра F, записанная в младшем разряде, означает 15, в следующем разряде – 15∙16 и т. д.

Таким образом, в современных информационных технологиях при создании программного обеспечения в основном используется двоичная система счисления, так как компьютеру легче оперировать большим числом простых элементов, чем небольшим числом сложных.

Заключение

В современной действительности люди используют многие системы счисления. Иногда мы даже сами не замечаем, что, например, мы пользуемся шестидесятеричной системой в часах, двенадцатеричной в календаре и т. д. Мы не замечаем их вокруг себя, но ведь без них мы уже не мыслим жизни. История отсортировала эти системы, и некоторые из них бесследно исчезли, но зато сейчас разные системы там, где их использовать удобнее. Например, человеку легче воспринимать короткие десятичные числа, а компьютеру удобнее работать с большим количеством простых сигналов в двоичных числах. За долгое время раскрылись преимущества и недостатки разных систем счисления, и сейчас они используются как раз там, где нужно.

www.hintfox.com

Системы счисления древнего мира — Космопорт

Изучение древних систем счисления и решение задачи с их применением.

Исследовательская работа:

«Системы счисления древнего мира»

«Математика – царица наук» - гласит известная поговорка. Главной её частью естественно являются цифры. Сейчас в мире используется более или менее общая, хорошо сформированная система. Но что было 3, 4, 5 тыс. лет назад?

И поэтому нашей главной целью является дать ответы на следующие вопросы:

• Какие государства имели более развитые системы счисления?
• Какие системы они использовали?
• Как развивались системы счисления?

Задачи: изучение материалов про системы счисления древности, решение современной задачи с использованием всех исследуемых систем.

Предмет исследования системы счисления древности.

Перед началом поиска информации мы определили следующие государства для изучения:

ØДревний Египет

ØВавилон

ØДревняя Греция

ØРим

ØКитай

ØИндия

1.Древний Египет

Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. Множество из десяти подковообразных символов, т.е. Число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. Число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона. Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) И московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи. Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. Дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителям Месопотамии

2.Вавилон

Письменность шумеров является, по-видимому, столь же древней, как и письменность египтян. Развитие способов представления чисел в Месопотамской долине вначале шло так же, как и в долине Нила, но затем жители Междуречья ввели совершенно новый принцип. Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались на солнце или в печи. Эти записи оказались исключительно долговечными, а потому, в отличие от египетских папирусов, дошедших до нас в весьма малом числе экземпляров, в музеях мира хранятся десятки тысяч клинописных табличек. Однако жесткость материала, на котором жители Месопотамии делали записи, оказала глубокое влияние на развитие числовых обозначений. Через некоторое время после того, как Аккад завоевал шумеров, система счисления в Месопотамии стала шестидесятеричной, хотя сохранилось также и основание 10. Казавшееся правдоподобным предположение относительно того, почему выбор пал на число 60 как на основу вавилонской системы счисления, и утверждавшие, будто это связано с тем, что продолжительность земного года считалась равной 360 дням, не получило подтверждения. Ныне принято считать, что шестидесятеричная система была выбрана из метрологических соображений: число 60 имеет много делителей.

3.Древняя Греция

В Древней Греции имели хождение две основных системы счисления – аттическая (или геродианова) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символГ, первую букву слова «пента» (пять) (буква Г употреблялась для обозначения звука «п», а не «г»). Дойдя до десяти, они ввели еще один новый символD, первую букву слова «дека» (десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символHозначал 100 (гекатон),X– 1000 (хилиои), символM– 10000 (мириои или мириада).

Ионическая система первоначально не сильно потеснила уже установившуюся аттическую или акрофоническую (по начальным буквам слов, означавших числительные) системы исчисления. По-видимому, официально она была принята в Александрии во времена правления Птолемея Филадельфийского и в последующие годы распространилась оттуда по всему греческому миру, включая Аттику. Переход к ионической системе счисления произошел в золотой век древнегреческой математики и, в частности, при жизни двух величайших математиков античности. Есть нечто большее, чем просто совпадение, в том, что именно тогда Архимед и Аполлоний работали над усовершенствованием системы обозначения больших чисел. Архимед, придумавший схему октад (эквивалентную современному использованию показателей степени числа 10) гордо заявлял в своем сочинении «Псаммит» («Исчисление песчинок»), что может численно выразить количество песчинок, необходимых для того, чтобы заполнить всю известную тогда Вселенную. Изобретенная им система обозначения чисел включала число, которое ныне можно было бы записать в виде единицы, за которой следовало бы восемьдесят тысяч миллионов цифр.

4.Рим

Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы. Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символыI,V,X,Q(илиЕ, илиД) иf. Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Дробей римляне избегали так же упорно, как и больших чисел.

5.Китай

Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять. Первые пять кратных числа 10 обозначались одной, двумя, пятью горизонтальными палочками, а одна, две, три и четыре горизонтальные палочки, к которым сверху приставлялась вертикальная палочка, означали числа 60, 70, 80 и 90.

Во второй китайской системе счисления для обозначения первых девяти целых чисел или символов используют девять различных знаков и одиннадцать дополнительных символов для обозначения первых одиннадцати степеней числа 10. В сочетании с умножением и вычитанием это позволяло записывать любое число меньше триллиона. Если один из символов, обозначающих первые девять целых чисел, стоит перед (при чтении слева направо) символом, означающим степень числа 10, то первое нужно умножить на второе, если же символ одного из девяти первых целых чисел стоит на последнем месте, то это число надлежит прибавить к обозначенному предыдущими символами.

6.Индия

Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счислениявытесни

cosmoport.club

История чисел и система счисления, позиционные системы (кратко)

История чисел и система счисления тесно взаимосвязаны, потому что система счисления и представляет собой способ записи такого абстрактного понятия, как число. Данная тема не относится сугубо к области математики, ведь всё это является важной частью культуры народа в целом. Потому, когда разбирается история чисел и систем счисления, кратко затрагиваются и многие другие аспекты истории создавших их цивилизаций. Системы в целом делятся на позиционные, непозиционные и смешанные. Из их чередования состоят вся история чисел и систем счисления. Позиционные системы – это такие, в которых величина, обозначаемая цифрой в записи числа, зависит от ее позиции. В непозиционных системах, соответственно, такой зависимости нет. Человечеством созданы и смешанные системы.

Изучение систем счисления в школе

Сегодня урок «История чисел и систем счисления» проводится в 9 классе в рамках курса по информатике. Главное практическое его значение – научить переводить числа из одной системы счисления в другую (прежде всего из десятиричной в двоичную). Однако история чисел и систем счисления является органической частью истории в целом и вполне могла бы дополнить также и этот предмет школьной программы. Также это могло бы улучшить пропагандируемый сегодня междисциплинарный подход. В рамках общего курса истории в принципе могла бы изучаться не только история экономического развития, социально-политических движений, правлений и войн, но и в небольшой степени история чисел и систем счисления. 9 класс в курсе информатики в таком случае можно было бы в части перевода чисел из одной системы в другую снабдить значительно большим число примеров из ранее пройденного материала. А примеры эти не лишены увлекательности, что и будет показано ниже.

Возникновение систем счисления

Сложно сказать, когда, а главное, как человек научился считать (так же, как невозможно доподлинно выяснить, когда, а главное, как возник язык). Известно только, что все древние цивилизации уже имели свои системы счёта, значит, история чисел и система счисления зародились в доцивилизационное время. Камни и кости не способны рассказать нам, что происходило в человеческом сознании, а письменных источников тогда ещё не создавали. Возможно, счёт понадобился человеку при разделе добычи или много позже, уже в ходе неолитической революции, то есть при переходе к земледелию, для раздела участков поля. Любые теории на этот счёт будут в равной степени беспочвенными. Но некоторые предположения всё же можно сделать, изучая историю различных языков.

Следы древнейшей системы счисления

Самая логичная начальная система счёта – противопоставление понятий «один» – «много». Логична она для нас потому, что в современном русском языке существует только единственное и множественное число. Но во многих древних языках было также и двойственное число для обозначения двух предметов. Существовало оно и в первых индоевропейских языках, включая древнерусский. Таким образом, история чисел и система счисления начались с разделения понятий «один», «два», «много». Однако уже в самых древних известных нам цивилизациях были разработаны более детальные системы счисления.

Месопотамская запись чисел

Мы привыкли, что система счисления десятирична. Это и понятно: на руках 10 пальцев. Но тем не менее история возникновения чисел и систем счисления прошла через более сложные фазы. Месопотамская система счисления – шестидесятиричная. Потому до сих пор в часе 60 минут, а в минуте – 60 секунд. Потому год делится на число месяцев, кратное 60, а день делится на такое же число часов. Изначально это были солнечные часы, то есть каждый из них составлял 1/12 светового дня (на территории современного Ирака его длительность не сильно варьировалась). Только много позже длительность часа стали определять не по солнцу и добавили также 12 ночных часов.

Интересно то, что записывались знаки этой шестидесятиричной системы, будто она десятиричная – существовало только два знака (для обозначения единицы и десятка, не шести и не шестидесяти, а именно десятка), цифры получали, комбинируя эти знаки. Страшно себе даже вообразить, как сложно было записать сколько-нибудь большое число таким способом.

Древнеегипетская система счисления

И история чисел в десятиричной системе счисления, и использование многочисленных значков для обозначения чисел началось с древних египтян. Они комбинировали иероглифы, которые обозначали один, сто, тысячу, десять тысяч, сто тысяч, миллион и десять миллионов, обозначая таким образом нужное число. Такая система была гораздо удобнее, чем месопотамская, использовавшая только два знака. Но при этом она имела явное ограничение: сложно было записать число, значительно большее, чем десять миллионов. Правда, древнеегипетская цивилизация, как и большинство цивилизаций Древнего мира, с такими числами не сталкивалась.

Эллинские буквы в математических записях

История европейской философии, науки, политической мысли и многого другого во многом начинается в Древней Элладе («Эллада» – это самоназвание, оно предпочтительнее, чем придуманное римлянами «Греция»). Развиты в этой цивилизации были и математические знания. Числа эллины записывали буквами. Отдельные буквы обозначали каждое число от 1 до 9, каждый десяток от 10 до 90 и каждую сотню от 100 до 900. Только тысячу обозначали той же буквой, что и единицу, но с другим знаком рядом с буквой. Система позволяла даже большие цифры обозначать относительно короткими надписями.

Славянская система счисления как наследница эллинской

История чисел и систем счисления была бы не полной без нескольких слов о наших предках. Кириллица, как известно, основана на эллинском алфавите, потому и славянская система записи цифр также была основана на эллинской. Здесь тоже отдельными буквами обозначалось каждое число от 1 до 9, каждый десяток от 10 до 90 и каждая сотня от 100 до 900. Только использовались не эллинские буквы, а кириллица, или глаголица. Существовала также и интересная особенность: несмотря на то что и эллинские тексты в то время, и славянские с самого начала их истории записывались слева направо, славянские цифры писались как бы справа налево, то есть буквы, обозначавшие десятки ставили правее букв, обозначавших единицы, буквы, обозначавшие сотни правее букв, обозначавших десятки и т. д.

Аттическое упрощение

Эллинские учёные достигли огромных высот. Римское завоевание не прервало их изысканий. Например, судя по косвенным свидетельствам, Аристарх Самосский за 18 веков до Коперника разработал Гелиоцентрическую систему мира. Во всех этих сложных расчётах эллинским учёным помогала их система записи чисел.

Но для простых людей, например, торговцев, система зачастую оказывалась слишком сложной: чтобы её использовать, требовалось запомнить числовые значения 27 букв (вместо числовых значений 10 символов, которые учат современные школьники). Потому появилась упрощённая система, получившая название аттической (Аттика – область Эллады, одно время лидировавшая в регионе в целом и особенно в морской торговле региона, так как столицей Аттики были знаменитые Афины). В этой системе отдельными буквами стали обозначаться только числа один, пять, десять, сто, тысяча и десять тысяч. Получается всего шесть знаков – их гораздо легче запоминать, а слишком сложных вычислений торговцы всё равно не производили.

Римские цифры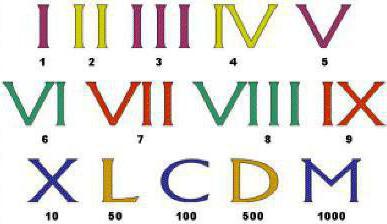

И система счисления, и история чисел древних римлян, и в принципе история их науки является продолжением эллинской истории. За основу была взята аттическая система, просто эллинские буквы заменили латинскими и добавили отдельное обозначение пятидесяти и пятисот. При этом сложные расчёты в своих трактатах учёные продолжали производить эллинской системой записи в 27 букв (да и сами трактаты они обычно писали по-эллински).

Римскую систему записи чисел нельзя назвать особо совершенной. В частности, она гораздо более примитивна, чем древнерусская. Но исторически сложилось так, что она до сих пор сохраняется наравне с арабскими (так называемыми) цифрами. И забывать эту альтернативную систему, переставать её использовать не стоит. В частности, сегодня часто арабскими цифрами обозначаются количественные числительные, а римскими – порядковые.

Великое древнеиндийское изобретение

Цифры, которые сегодня используем мы, появились изначально в Индии. Точно не известно, когда история чисел и система счисления сделали этот знаменательный поворот, но, скорее всего, не позднее V века от Рождества Христова. Часто подчёркивается, что именно индийцы разработали понятие нуля. Такое понятие было известно математикам и других цивилизаций, но действительно лишь система индийцев позволила полноценно включить его в математические записи, а значит, и в вычисления.

Распространение индийской системы счисления по Земле

Предположительно в IX веке индийские цифры заимствовали арабы. В то время как европейцы пренебрежительно относились к античному наследию, а в некоторые регионах одно время даже намеренно уничтожали его как языческое, арабы бережно хранили достижения древних греков и римлян. С самого начала их завоеваний ходовым товаром стали переводы античных авторов на арабский. В основном через трактаты арабских учёных средневековые европейцы снова обрели наследие древних мыслителей. Вместе с этими трактатами пришли и индийские цифры, которые в Европе стали называть арабскими. Они не сразу были приняты, потому что для большинства людей оказались менее понятными, чем римские. Но постепенно удобство математических расчётов с помощью этих знаков победило невежественность. Лидерство европейских промышленно развитых стран привело к тому, что так называемые арабские цифры распространились по всему миру и сегодня применяются практически повсеместно.

Двоичная система счисления современных компьютеров

С появлением компьютеров постепенно совершили значительный поворот многие области знаний. Не стала исключением история чисел и систем счисления. Фото первого компьютера мало напоминает современное устройство, на мониторе которого вы читаете эту статью, но работа их обоих основана на двоичной системе счисления, коде, состоящем, только из нулей и единиц. Для обыденного сознания всё же остаётся удивительным, что с помощью комбинации из всего двух символов (фактически сигнала или его отсутствия) можно производить самые сложные вычисления и автоматически (при наличии соответствующей программы) переводить числа в десятиричной системе исчисления в числа в двоичной, шестнадцатиричной, шестидесятишестиричной и любой другой системе. И с помощью такого двоичного кода на мониторе изображается данная статья, где отражена история чисел и система счисления у разных цивилизаций в истории.

fb.ru

История чисел и систем счисления

С древнейших времён перед людьми стояла проблема обозначения (кодирования) числовой информации.

Маленькие дети показывают свой возраст на пальцах. Лётчик сбил самолёт, ему за это рисуют звёздочку, Робинзон Крузо считал дни зарубками.

 Числом обозначали некоторые реальные объекты, свойства которых были одинаковы. Когда мы что-то считаем или пересчитываем, мы как бы обезличиваем предметы, т.е. подразумеваем, что их свойства одинаковы. Но самым главным свойством числа является наличие объекта, т.е. единица и его отсутствие, т.е. ноль.

Что такое цифра?

Это алфавит чисел, набор символов, с помощью которых мы кодируем числа. Цифры – числовой алфавит.

Цифры и числа – это разные вещи! Рассмотрим два числа 5 2 и 2 5. Цифры одни и те же – 5 и 2.

А чем эти числа отличаются?

Порядком цифр? – Да! Но лучше сказать - позицией цифры в числе.

Давайте подумаем, что же это такое системы счисления?

Это запись чисел? Да! Но мы не можем писать так, как нам вздумается - нас должны понимать другие люди. Поэтому необходимо ещё использовать и определенные правила их записи.

Понятие системы счисления

       Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти всем хорошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления.

 В позиционных системах счисления  значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

        Непозиционные   системы счисления возникли раньше позиционных, поэтому рассмотрим сначала различные непозиционные системы счисления.

Непозиционные системы счисления

Непозиционной системой счисления  называется такая система счисления, у которой количественный эквивалент (вес) цифры не зависит от ее местоположения в записи числа.

 К непозиционным системам относятся: римская система счисления, алфавитные системы счисления и другие.

Сначала люди  просто различали ОДИН предмет перед ними или нет. Если предмет был не один, то говорили МНОГО.

Первыми понятиями математики были "меньше",  "больше",  "столько же".

            Если одно племя меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. Достаточно было положить рядом с каждой рыбой по ножу, чтобы обмен между племенами состоялся.

         Счет появился тогда, когда человеку потребовалось сообщать своим соплеменникам о количестве найденных им предметов.

И, так как многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.

Имена числительные во многих языках указывают, что у первобытного человека орудием счета были преимущественно пальцы.       Пальцы оказались прекрасной вычислительной машиной. С их помощью можно было считать до 5, а если взять две руки, то и до 10.

Пальцевой счет сохранился кое-где и поныне. Например, на крупнейшей мировой хлебной бирже в Чикаго предложения и запросы, как и цены объявляются маклерами на пальцах без единого слова.

         Запоминать большие числа было трудно, поэтому к счетной машине рук и ног стали добавлять различные приспособления.  Появилась потребность в записи чисел.

Количество предметов изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине…

Единичная (палочная) система счисления  

Любое число в ней образуется повторением одного знака - единицы.      Археологами найдены такие "записи" при раскопках культурных слоев, относящихся к  периоду палеолита 10-11 тысяч лет до н.э.

        Чем больше зерна собирали люди со своих полей, чем многочисленнее становились их стада, тем большие числа становились им нужны.

        Единичная запись для таких чисел была громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа.

Древнеегипетская  десятичная система счисления

(2,5 тысяч лет до н.э. )

      Пример1. Запишите число 1 245 386  в древнеегипетской записи

     С операциями сложения и вычитания люди имели дело задолго до того, как числа получили имена.

     Когда несколько групп сборщиков кореньев или рыболовов складывали в одно место свою добычу, они выполняли операцию сложения.

     С операцией умножения люди познакомились, когда стали сеять хлеб и увидели, что собранный урожай в несколько раз больше, чем количество посеянных семян.

     Когда добытое мясо животных или собранные орехи делили поровну между всеми "ртами", выполнялась операция деления.

Как  же  египтяне  считали?

     Умножение и деление египтяне производили путем последовательного удвоения чисел.

Пример. 19 * 31

   Египтяне последовательно удваивали число 31. В правом столбце записывали результаты удвоения, а в левом - соответствующую степень двойки.

Египетские дроби всегда имели в числителе единицу (исключение составляло 2/3).      Дроби записывались как натуральные числа, только над ними ставилась точка.

Исключение: специальные знаки были для 1/2 и для 2/3.

Римская  десятичная система счисления

(2 тысячи  лет до н.э. и до наших дней)

Самой распространенной из непозиционных систем счисления является римская система.

Главная проблема с римскими цифрами заключается в том, что сложно производить умножение и деление. Другим недостатком римской системы является: Запись больших чисел требует введения новых символов. А дробные числа можно записывать только как отношение двух чисел. Тем не менее, они были основными до конца средних веков. Но и в наше время их ещё используют.

Вспомните где?

Значение цифры не зависит от ее положения в числе.

Например, в числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину - число 10, три числа по 10 в сумме дают 30.

Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа - прибавляется.

Запомните: 5, 50, 500 не повторяются! 

А какие могут повторяться?

Если слева от старшей цифры стоит младшая, то она отнимается. Если младшая цифра стоит справа от старшей, то она прибавляется - I, X, C, M могут повторяться до 3-х раз.

Например:

1)      MMIV = 1000+1000+5-1 = 2004

2)      149 =  (Сто - C, сорок - XL, а девять - IX) = CXLIX

Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом: МСМХСVIII = 1000 + (1000 - 100) + (100 - 10) + 5 + 1 + 1 + 1.

Алфавитные системы счисления

Алфавитные непозиционные системы счисления были распространены у древних армян, грузин, греков (альфа, бэта, гамма), арабов, евреев, и других народов Ближнего Востока, а также у славян (аз, буки, веди).

В старину на Руси широко применялись системы счисления, напоминающие систему Древнего Египта.   С их помощью сборщики податей заполняли квитанции об уплате подати (ясака) и делали записи в податной тетради. Например, 1232 руб. 24 коп.                                                      Звезда – тысяча рублей                                                      Колесо – сто рублей                                                      Квадрат – десять рублей                                                      Х   - рубль                                                      |  - копейку.

В IX веке монахами братьями Кириллом и Мефодием   была создана новая нумерация вместе со славянской алфавитной системой для перевода священных библейских книг.

Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел.

Эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии  до реформы Петра I  (до конца XVII века).   - титло

Удобны ли алфавитные системы?

Недостатки непозиционных систем счисления:

1.  Существует постоянная  потребность введения новых знаков для записи больших чисел.

2.  Невозможно представлять дробные и отрицательные числа.

3.   Сложно выполнять арифметические операции,   так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.

   Вплоть до конца средневековья не существовало никакой универсальной системы записи чисел. Только с развитием математики, физики, техники, торговли, финансовой системы возникла потребность в единой универсальной системе счисления, хотя и сейчас многие племена, нации и народности используют другие системы счисления.

   Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.

           Далее рассмотрим позиционные системы счисления.

Позиционной системой счисления  называется такая система счисления, у которой количественный эквивалент (вес) цифры зависит от ее местоположения в записи числа.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.

За основание можно принять любое натуральное число — два, три, четыре, ..., образовав новую позиционную систему: двоичную, троичную, четверичную и ...

   Десятичная позиционная система счисления

      Индийские ученые сделали одно из важнейших в математике открытий - изобрели позиционную систему счисления, которой теперь пользуется весь мир. Ал-Хорезми подробно описал индийскую арифметику в своей книге.

Триста лет спустя (в 1120 г.) эту книгу перевели на латинский язык, и она стала первым учебником "индийской" арифметики для всех европейских городов.

Основания, используемые в наши дни:

                    - 10 у привычной десятичной системы счисления (десять пальцев на руках). Алфавит: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0

           - 60 придумано в Древнем Вавилоне: деление часа на 60 минут, минуты — на 60 секунд, угла — на 360 градусов.

 - 12 распространили англосаксы: в году 12 месяцев, в сутках два периода по 12 часов, в футе 12 дюймов

                     - 7 используется для счета дней недели

Домашнее задание: - выучить определение "система счисления" и классификацию СС

                                                   1. Какие числа записаны с помощью римских цифр: МСIХ, LХV?

                                                   2. Запишите год своего рождения:

                                                                   а) в древнеегипетской системе счисления;

                                                                   б) в римской системе счисления;

                                                                   в) в древнеславянской системе счисления.

informatika.edusite.ru

Этапы развития систем счисления

Эволюция систем счисления

Определения

Система счисления — это знаковая система, в которой числа записываются по определённым правилам с помощью символов некоторого алфавита , называемых цифрами .

Числа: под числом понимается его величина, а не символьная запись. Например, 123, 1010011, CXL

Цифры – символы, при помощи которых записывается число. Например, 0, 1, 2, … I, V, X, L, …

Алфавит – это набор цифр . {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

{0, 1}

{0, 1, … , A, B, C, D, E, F}

Унарная система счисления

простейшая и самая древняя

Для записи любых чисел используется всего один символ:

1

|

2

||

3

|||

4

||||

5

|||||

зарубка.

узелок

палочка

ГРУППЫ СИСТЕМ СЧИСЛЕНИЯ

Аддитивные системы счисления

Используется не одна, а несколько цифр. Они могут изображаться как угодно, но разные цифры должны выглядеть по-разному.

Для того, чтобы прочесть число, нужно было сложить значения всех цифр. Поэтому такие системы назвали аддитивными ( add добавлять, складывать, англ.).

Египетская нумерация

В Египте единицы записывали палочками , а десяток палочек заменяли на изображение пут для коров , десяток пут - одна мерная веревка , и т. д.

1

10

100

1 000

10 000

100 000

1 000 000

10 000 000

Записывались цифры числа начиная с больших значений и заканчивая меньшими Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду. Удобств для счета никаких.

Задание:

=1 205

=1 023 029

Нумерация индейцев Майя

Задание:

20+20+5+5+5+1+1+1+1 = 59;

5+5+5+1 = 16;

20+1+1+1 = 23

Записывались цифры числа в столбик, начиная со знаков , затем знаки , а потом больших значений и заканчивая меньшими.

Сначала эта нумерация обслуживала пятеричную систему счисления, а потом ее приспособили для двадцатеричной.

Древнерусская система счисления

В старину на Руси применялась система счисления, с помощью которой сборщики податей заполняли квитанции и делали записи в податной тетради.

Задание:

= 1 232 руб. 24 коп.

Алфавитные аддитивные системы счисления

Римляне

Славяне

Греки

Евреи

Арабы

Сирийцы

Для записи чисел использовалась большая часть алфавита того народа, который использовал эту систему.

Древняя греческая нумерация

В древнейшее время в Греции была распространена аттическая нумерация .

Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000.

Числа в пределах первого десятка тысяч записывались так:

Задание:

=7800

=382

Аттическая нумерация была вытеснена у греков более компактной буквенной нумерацией, так называемой ионийской системой .

Первые девять букв обозначали единицы от 1 до 9, следующие девять – десятки от 10 до 90, остальные четыре – сотни от 100 до 400.

Славянская глаголическая нумерация

Система была создана для записи чисел в священных книгах западных славян .

Использовалась нечасто, но достаточно долго: с VIII по XIII в.

По организации в точности повторяет греческую нумерацию.

Задание:

800 + 60 + 3 = 863

Для того, чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.

Славянская кириллическая нумерация

Эта нумерация была создана вместе со славянской алфавитной системой для переписки священных книг для славян греческими монахами братьями Кириллом (Константином) и Мефодием в IX веке.

До сих пор православные церковные книги используют эту нумерацию. Запись числа, использованная славянами аддитивная:

Задание:

800 + 60 + 3 = 863

Римская система счисления

Цифры обозначаются буквами латинского алфавита. Чтобы выделить числа в тексте, над ними рисовали черту: LXIV. Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте.

I – 1 (палец),

V – 5 (раскрытая ладонь, 5 пальцев) ,

X – 10 (две ладони) ,

L – 50,

C – 100 ( Centum ) ,

D – 500 ( Demimille ) ,

M – 1000 ( Mille )

Римская система счисления

Правило :

• не ставят больше трех одинаковых цифр подряд. Комбинация из 4-х одинаковых цифр заменяется комбинацией с правилом вычитания - если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы: 40 = XXXX = XL (50-10)
• не ставят больше трех одинаковых цифр подряд. Комбинация из 4-х одинаковых цифр заменяется комбинацией с правилом вычитания - если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы: 40 = XXXX = XL (50-10)

Примеры :

MDC X L I V =

– 1

= 1644

+ 5

+ 50

– 10

+ 100

+ 500

1000

2389 = 2000 + 300 + 80 + 9

M M

CCC

LXXX

IX

2389 = M M C C C L X X X I X

14

Римская система счисления

Примеры:

Число 32 в римской системе счисления имеет вид:

XXXII = (X+X+X)+(I+I)= 30+2

Число 444 (в десятичной записи 3 одинаковые цифры), в римской системе счисления будет записано в виде:

CDXLIV = 400+40+4 = (D-C)+(L-X)+(V-I)

Число 1974 в римской системе счисления имеет вид:

MCMLXXIV= 1000+900+50+20+4 = M+(M-C)+L+(X+X)+( I V)

Задание : запишите числа в римской системе счисления

3768 =

МММ DCCLXVIII

2983 =

ММ CMIICIII

1452 =

М CDLII

1999 =

М CMXCIX

14

14

Задания:

• Запишите в десятичной системе счисления римские числа:

• XI X; 2) L X ; 3) C X L; 4) C D LX IX;

5) CMXLVI; 6) CCMLXXX; 7) MDCXLVIII ; 8) MMCXC .

2. Запишите в римской системе счисления:

• 13 ; 2) 99 ; 3) 666 ; 4) 444 ; 5) 1692 ;

6) 146; 7) 301; 8) 959; 9) 2078; 10) 699.

• 1 9 ; 2) 60 ; 3) 140 ; 4) 4 6 9 ;

5) 946; 6) 880; 7) 1648 ; 8) 2190 .

1) XIII; 2) XCIX; 3) DCLXVI; 4) CDXLIV; 5) MDCXCII ;

6) CIVVI; 7) CCDI; 8) CMLIX; 9) MMLXXVIII; 10) DCXCIX.

3 . Выполните действия и запишите результат в римской системе счисления:

1) XXII – V; 2) CV – LII; 3) XCIX + XIX; 4) MCM + VIII;

5) XX : V; 6) X * IV; 7) LXVI : XI ; 8) XXIV * VII.

1) 17=XVII; 2) 53=LIII; 3) 118=CXVIII; 4) 1908=MCMVIII; 5) 4=IV; 6) 40=LX; 7) 6=V1; 8) 168=CLXVIII.

4. Какие десятичные числа записаны с помощью римских цифр? Выделите разряды:

1) MMMCCDXXXIII; 2) DCCLXXVII; 3) DCIX; 4) MCMXCVI; 5) MMII; 6) MMCCDXIII; 7) XLVII; 8) CCMVIII.

1) 3 333 ; 2) 777 ; 3) 60 9; 4) 1996 ; 5) 2002; 6) 2313; 7) 47; 8) 808 .

Мультипликативные системы счисления

Для записи чисел используется определенное количество цифр, которые могут принимать разные значения в зависимости от расположения в записи числа. Такие системы счисления были только у народов с очень хорошо развитой математикой.

Чтобы "собрать« число используется умножение ( multiplication англ.). Например, запись числа 1999 означает:

1 х 1000 + 9 х 100 + 9 х 10 + 9.

Такая система счисления годится для записи чисел, и она очень удобна для счета.

Китайская нумерация

Эта нумерация использовала те же принципы, что и современная арабская, которой мы пользуемся.

Возникла в Китае около 4 000 лет назад.

1 х 1000 = 1000

5 х 100 + 4 х 10 + 8 = 548

Задание:

=2425

Вавилонская нумерация

Цифры имели клинообразный вид - писали на глиняных табличках палочками треугольной формы.

Ту роль, которую у нас играет число 10, в вавилонской нумерации играет число 60.

Эту нумерацию называют шестидесятиричной .

3

единица

десяток

пробел

разделение разрядов

нуль

20

32

59

Задание:

5 х 60 + 2 = 302

1 х 60 х 60 + 2 х 60 + 5 = 3725

Арабская нумерация

Арабские цифры сложились в Индии около 400 г. Арабы стали пользоваться подобной нумерацией около 800 г., а примерно в 1200 г. ее начали применять в Европе, где арабские цифры стали известны благодаря трудам арабских математиков, и потому за ними утвердилось название «арабские»

Арабская нумерация вначале была буквенной. Традиционные арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму.

Первоначально этими знаками представлялись числа 1, 2, 3, … 9, 10, 20, 30, …, 90, 100, 1000. С их помощью записывались другие числа. Но в последствии был введен особый знак - жирная точка для указания пустующего разряда. И нумерация "Деванагари" превратилась в поместную десятичную систему.

Арабская нумерация

Решающую роль в распространении индийской нумерации в арабских странах сыграла книга «Об индийском счёте», написанная в начале IX века Мухаммедом Ал Хорезми.

В XII веке эта книга была переведена на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении индо-арабских цифр.

Из арабского языка заимствовано и слово «цифра» (по-арабски "сыфр"), означающее буквально « пустое место ». Это слово применялось для названия знака пустого разряда, и этот смысл сохраняло до XVIII века, хотя еще в XV веке появился латинский термин "нуль" (nullum - ничто).

В России до конца XVII века сохранялась славянская нумерация.

При Петре I возобладала так называемая "арабская нумерация".

Леонардо Пизанский

Форма индийских цифр претерпевала многообразные изменения. Та форма, которой мы сейчас пользуемся установилась в XVI веке.

Начало использования арабских цифр в Европе было положено итальянским математиком средневековой Европы Леона́рдо Пиза́нски м , известным как Фибоначчи . Он долгое время жил на Востоке, где и познакомился с математикой арабов.

Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака», которая содержит почти все арифметические и алгебраические сведения того времени,

По этой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления.

intolimp.org

История возникновения систем счисления.

 Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Лекция 1. Системы счисления 1. История возникновения систем счисления. 2. Позиционные и непозиционные системы счисления. 3. Десятичная система счисления, запись чисел в ней. 4. Разряды   Человеку постоянно приходится иметь дело с числами, поэтому нужно уметь правильно называть и записывать любое число, производить действия над числами. Как правило, все с этим успешно справляются. Помогает здесь способ записи чисел, который в настоящее время используется повсеместно и носит название десятичной системы счисления. Изучение этой системы начинается в начальных классах, и , конечно, учителю нужны определенные знания в этой области. Он должен знать различные способы записи чисел, алгоритмы арифметических действий и их обоснование. Материал данной лекции дает тот минимум, без которого невозможно разобраться с различными методическими подходами к обучению младших школьников способам записи чисел и выполнению над ними действий. История возникновения систем счисления. Понятие числа возникло в глубокой древности. Тогда же появилась необходимость в названии и записи чисел. Язык для наименования, записи чисел и выполнения действий над ними называют системой счисления. Простейшая система записи натуральных чисел требует лишь одной цифры, например «палочки» (или зарубки на дереве, как у первобытного человека, или узелка на веревке, как у индейцев Америки), которая изображает единицу. Повторяя этот знак, можно записать любое число: каждое число n записывается просто n «палочками». В такой системе счисления удобно выполнять арифметические действия. Но подобный способ записи очень не экономичен и для больших чисел неизбежно приводит к ошибкам в счете. Поэтому со временем возникли иные, более экономичные и удобные способы записи чисел. Рассмотрим некоторые из них. В Древней Греции была распространена так называемая аттическая нумерация. Числа 1, 2, 3, 4 обозначались черточками: . Число 5 записывалось знаком Г (древнее начертание буквы «пи», с которой начинается слово «пенте» - пять). Числа 6, 7, 8, 9 обозначались так: Число 10 обозначалось Δ (начальной буквой слова «дека» - десять). Числа 100, 1000 и 10 000 обозначались Н, Х, М – начальными буквами соответствующих слов. Другие числа записывались различными комбинациями этих знаков. В третьем веке до нашей эры аттическая нумерация была вытеснена так называемой ионийской системой. В ней числа 1 – 9 обозначаются первыми девятью буквами алфавита: α (альфа), β (бэта), γ (гамма), δ (дельта), ε (эпсилон), ς (фау), ζ (дзета), η (эта), (тэта). Числа 10, 20, 30, 40, 50, 60, 70, 80, 90 – следующими девятью буквами: i (йота),κ (каппа), λ (ламбда), μ (мю), ν (ню), ξ (кси), ο (омикрон), π (пи), с (копа). Числа 100, 200, 300, 400, 500, 600, 700, 800, 900 – последними девятью буквами греческого алфавита. Алфавитную нумерацию, подобную древнегреческой, имели в древности евреи, арабы и многие другие народы Ближнего Востока. У какого народа она возникла впервые неизвестно. В Древнем Риме в качестве «ключевых» использовались числа 1, 5, 10, 50, 100, 500 и 1000. Они обозначались соответственно буквами I, V, X, L, C, D и М. Все целые числа (до 5000) записывались с помощью повторения выше приведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей: VI = 6, т.е. 5 + 1; IV = 4, т.е. 5 – 1;XL = 40, т.е. 50 – 10; LX = 60, т.е. 50 + 10. Подряд одна и та же цифра ставится не более трех раз: LXX = 70, LXXX = 80, число 90 записывается XC (а не LXXXX). Например: XXVIII = 28, XXXIX = 39, CCCXCVII = 397, MDCCCXVIII = 1818. Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Однако римская нумерация сохранилась до настоящего времени. Ее используют для обозначения юбилейных дат, наименования конференций, глав в книгах и т.д. На Руси в старину цифры обозначались буквами. Для указания того, что знак является не буквой, а цифрой, сверху над ними ставился специальный знак, называемый «титло». Первые девять цифр записывались так: Десятки обозначались так: Сотни обозначались так: Тысячи обозначались теми же буквами с «титлами», что и первые девять цифр, но у них слева ставился знак «≠»: ≠А = 1000, ≠В = 2000, ≠Е = 5000. Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками: = 10 000, = 20 000, = 80 000.   Отсюда произошло выражение «Тьма народу», т.е. очень много народу. Сотни тысяч назывались «легионами», их обозначали, обводя знаки единиц кружками из точек: = 100 000, = 200 000, = 800 000. Миллионы назывались «леодрами». Их обозначали, обводя знаки единиц кружками из лучей или запятых: = 1 000 000, = 2 000 000.   Десятки миллионов назывались «воронами» или «вранами» и их обозначали, обводя знаки единиц кружками из крестиков или ставя по обе стороны букву К: Сотни миллионов назывались «колодами». «Колода» имела специальное обозначение – над буквой и под буквой ставились квадратные скобки: = 100 000 000. Иероглифы жителей Древнего Вавилона составлялись из узких вертикальных и горизонтальных клинышков, эти два значка использовались и для записи чисел. Один вертикальный клинышек обозначал единицу, горизонтальный – десяток. В Древнем Вавилоне считали группами по 60 единиц. Например, число 185 представлялось как 3 раза по 60 и еще 5. Записывалось такое число с помощью всего двух знаков, один из которых обозначал, сколько раз взято по 60, а другой - сколько взято единиц. О том, когда и как возникла у вавилонян шестидесятеричная система, существует много гипотез, но ни одна пока не доказана. Одна из гипотез, состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывают с числом 60. Шестидесятеричная система, в некоторой степени, сохранилась до наших дней, например, в делении часа на 60 минут, а минуты - на 60 секунд и в аналогичной системе измерение углов: 1 градус равен 60 минутам, 1 минута – 60 секундам. Двоичной системой счисления пользовались при счете некоторые первобытные племена, она была известна еще древнекитайским математикам, но по настоящему развил и построил двоичную систему великий немецкий математик Лейбниц, видевший в ней олицетворение глубокой метафизической истины. Двоичной системой счисления пользуются некоторые (местные) культуры в Африке, Австралии и Южной Америке. Для изображения чисел в двоичной системе счисления требуется лишь две цифры: 0 и 1. По этой причине двоичную запись числа легко представить, пользуясь физическими элементами, которые имеют два различных устойчивых состояния. Именно это и послужило одной из важных причин широкого использования двоичной системы в современных электронных вычислительных машинах. Самой экономичной из всех систем счисления является троичная. Двоичная и равносильная ей, в смысле экономичности, четверичная системы, несколько уступают в этом отношении троичной, но превосходят все основные возможные системы. Если для записи чисел от 1 до 10 в десятичной системе требуется 90 различных состояний, а в двоичной – 60, то в троичной системе достаточно 57 состояний. Наиболее привычная ситуация, в которой проявляется необходимость троичного анализа, - это, пожалуй, взвешивание на чашечных весах. Здесь могут возникнуть три разных случая: либо одна из чашек перевесит другую, либо наоборот, либо же чашки уравновесят друг друга. Четверичной системой счисления пользуются, главным образом, индейские племена Южной Америки и индейцы юкки в Калифорнии, считающих на промежутках между пальцами. Пятеричная система счислениябыла распространена гораздо шире, чем все остальные. Индейцы племени таманакос в Южной Америке употребляют для обозначения числа 5 то же слово, что и для обозначения «всей руки». Слово «шесть» по-таманакски означает «один палец на другой руке», семь – «два пальца на другой руке» и т.д. для восьми и девяти. Десять называется «двумя руками». Желая назвать число от 11 до 14, таманакос протягивают вперед обе руки и считают: «один на ноге, два на ноге» и т.д. до тех пор, пока не доходят до 15 – «всей ноги». Затем следует «один на другой ноге» (число 16) и т.д. до 19. Число 20 по-таманакски означает «один индеец», 21 – «один на руке другого индейца». «Два индейца» означают 40, «три индейца» - 60. У жителей древней Явы и у ацтеков продолжительность недели составляла 5 дней. Некоторые историки считают, что римское число X (десять) составлено из двух римских пятерок V (одна из них перевернута), а число V в свою очередь возникло из стилизованного изображения человеческой руки. Широкое распространение имела в древности двенадцатеричная система счисления. Происхождение ее тоже связано со счетом на пальцах. А именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимают за единицу следующего разряда. Основное преимущество двенадцатеричной системы состоит в том, что ее основание делится без остатка на 2, 3 и 4. Сторонники двенадцатеричной системы появились еще в XVI веке. В более позднее время к их числу принадлежали столь выдающиеся люди, как Герберт Спенсер, Джон Квинси Адамс и Джордж Бернард Шоу. Существует даже американское двенадцатеричное общество, выпускающее два периодических издания: «Двенадцатеричный бюллетень» и «Руководство по двенадцатеричной системе». Всей «двенадцатеричников» общество снабжает специальной счетной линейкой, в которой в качестве основания используется 12. В устной речи остатки двенадцатеричной системы сохранились и до наших дней: вместо того, чтобы сказать «двенадцать», часть говорят «дюжина». Сохранился обычай считать многие предметы не десятками, а именно дюжинами, например, столовые приборы в сервизе (сервиз на 12 персон) или стулья в мебельном гарнитуре. Название единицы третьего разряда в двенадцатеричной системе счисления – гросс – встречается теперь редко, но в торговой практике начала XX столетия оно бытовало и, еще сто лет назад, его можно было легко встретить. Например, в написанном в 1928 году стихотворении «Плюшкин» В.В. Маяковский, высмеивая мещан, скупающих подряд все нужное и ненужное, писал: ..Оглядев товаров россыпь, в жадности и в алчи укупил

megapredmet.ru

«Системы счисления Древнего мира»

litcey.ru

Смотрите также

• История древней месопотамии
• 
  Цивилизация древний рим
• 
  Произведения древней руси
• 
  Занятия древнего человека
• 
  Древнейший человек это
• 
  Древней руси меры
• Философия древнего индии
• 
  Древний каирн skyrim
• 
  Stellaris древнее убежище
• 
  Оружие древних египтян
• 
  Древние боги лавкрафта