Дроби: история дробей. История возникновения обыкновенных дробей. Дроби в древнем риме

Дроби в Древнем Риме.

Римляне пользовались, в основном, только конкретными дробями, которые заменяли абстрактные части подразделами используемых мер. Эта система дробей основывалась на делении на 12 долей единицы веса, которая называлась асс. Так возникли римские двенадцатеричные дроби, т.е. дроби у которых знаменатель всегда был двенадцать. Двенадцатую долю асса называли унцией. Вместо 1\12 римляне говорили «одна унция», 5\12 – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной.

А путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия. Всего применялось 18 различных названий дробей. Например, в ходу были такие названия:

“скрупулус” - 1/288 асса,

”семис”- половина асса,

“секстанс”- шестая его доля,

“семиунция”- половина унции, т.е. 1/24 асса и т.д.

Чтобы работать с такими дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию ( 2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.

Унция обозначалась чертой - ,половина асса (6 унций) – буквой S (первой в латинском слове Semis-половина). Эти два знака служили для записи любой двенадцатеричной дроби, каждая из которых имела свое название. Например, 7\12 записывались так: S-.

Ещё в первом веке до нашей эры выдающийся римский оратор и писатель Цицерон говорил: “Без знания дробей никто не может признаваться знающим арифметику!”.

Дата добавления: 2015-09-04; просмотров: 306 | Нарушение авторских прав

mybiblioteka.su

История происхождения дробей - Документ

История происхождения дробей

Чуйко А.В.

5, ОШ ст.Шокай

Рук. Риплингер Л.А.

Введение

Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.

Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.

Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.

Дроби в Древнем Риме

У римлян основной единицей измерения массы,а также и денежной единицей служил «асс». Асс делился на 12 равных частей - унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12… Со временем унции стали применяться для измерения любых величин.

Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной.

Дроби в Древнем Египте

На протяжении многих веков египтяне именовали дроби “ломаным числом”, а первая дробь с которой они познакомились была 1/2. За ней последовали 1/4, 1/8, 1/16, …, затем 1/3, 1/6, …, т.е. самые простые дроби называемые единичными или основными дробями. У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами.

В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.

Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.

Одним из первых известных упоминаний о египетских дробях является математический папирус Ринда. Три более древних текста, в которых упоминаются египетские дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 2/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.

Египтяне ставили иероглиф

У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (большие чем 1/2).

Остальные дроби они записывали в виде суммы долей. Дробь они записывали в виде ,но знак «+» не указывали. А сумму

Вавилонские шестидесятеричные дроби

Жители древнего Вавилона примерно за три тысячи лет до нашей эры создали систему мер аналогичную нашей метрической, только в основе её лежало не число 10, а число 60, в которой меньшая единица измерения составляла часть высшей единицы. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд.

Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты.

Шестидесятые доли были привычны в жизни вавилонян. Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602, 603 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями.

Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360 градусов, градуса на 60 мин., минуты на 60с.

Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическими дробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.

Нумерация и дроби в Древней Греции

Поскольку греки работали с обыкновенными дробями лишь эпизодически, они использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятиричным дробям.

Недостатки греческих обозначений дробных чисел, включая использование шестидесятиричных дробей в десятичной системе счисления, объяснялись отнюдь не пороками основополагающих принципов. Недостатки греческой системы счисления можно отнести скорее за счет их упорного стремления к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали как набор единиц, поэтому то, что мы теперь рассматриваем как единое рациональное число – дробь, – греки понимали как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.

Дроби на Руси

В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находим следующие названия дробей на Руси:

Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.

Дроби в других государствах древности

В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями.

У индийского математика Брахмагупты мы находим достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.

Арабы первыми начали отделять чертой числитель от знаменателя.

Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. Иордан Неморарий (XIII ст.) выполняет деление дробей с помощью деления числителя на числитель и знаменателя на знаменатель, уподобляя деление умножению. Для этого приходится члены первой дроби дополнять множителями:

В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.

Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.

Десятичные дроби

           Появились десятичные дроби в трудах арабских математиков в Средние века и независимо от них в древнем Китае. Но и раньше, в древнем Вавилоне, использовали дроби такого же типа, только шестидесятеричные.

Позднее учёный Гартман Бейер (1563-1625) выпустил сочинение “Десятичная логистика”, где писал: “…я обратил внимание на то, что техники и ремесленники, когда измеряют какую-нибудь длину, то очень редко и лишь в исключительных случаях выражают её в целых числах одного наименования; обыкновенно им приходится или брать мелкие меры, или обращаться к дробям. Точно так же астрономы измеряют величины не только в градусах, но и в долях градуса, т.е. минутах, секундах и т.п. Их деление на 60 частей не так удобно, как деление на 10, на 100 частей и т.д., потому что в последнем случае гораздо легче складывать, вычитать и вообще производить арифметические действия; мне кажется, что десятичные доли, если бы ввести вместо шестидесятеричных, пригодились бы не только для астрономии, но и для всякого рода вычислений”.

Сегодня мы пользуемся десятичными дробями естественно и свободно. Однако то, что кажется естественным нам, служило настоящим камнем преткновения для учёных Средневековья. В Западной Европе 16 в. вместе с широко распространённой десятичной системой представления целых чисел в расчётах повсюду применялись шестидесятеричные дроби, восходящие ещё к древней традиции вавилонян. Понадобился светлый ум нидерландского математика Симона Стевина, чтобы привести запись и целых, и дробных чисел в единую систему. По-видимому, толчком создания десятичных дробей послужили составленные им таблицы сложных процентов. В 1585 г. он опубликовал книгу “Десятина”, в которой объяснил десятичные дроби.

С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. В Англии в качестве знака, отделяющего целую часть от дробной, была введена точка. Запятая, как и точка, в качестве разделительного знака была предложена в 1617 году математиком Непером.

Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.

Литература:

1. М.Я.Выгодский “Арифметика и алгебра в Древнем мире”(М. Наука,1967г)

2. Г.И.Глейзер “История математики в школе”(М. Просвещение,1964г)

3. И.Я.Депман “История арифметики” (М. Просвящение, 1959г)

textarchive.ru

история дробей. История возникновения обыкновенных дробей

Одним из самых сложных разделов математики по сей день считаются дроби. История дробей насчитывает не одно тысячелетие. Умение делить целое на части возникло на территории древнего Египта и Вавилона. С годами усложнялись операции, проделываемые с дробями, менялась форма их записи. У каждого государства древнего мира были свои особенности во «взаимоотношениях» с этим разделом математики.

Что такое дробь?

Когда возникла необходимость делить целое на части без лишних усилий, тогда и появились дроби. История дробей неразрывна связана с решением утилитарных задач. Сам термин «дробь» имеет арабские корни и происходит от слова, обозначающего «ломать, разделять». С древних времен в этом смысле мало что изменилось. Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы. Соответственно, примеры с дробями представляют собой последовательное выполнение математических операций с долями чисел.

Сегодня различают два способа их записи. Обыкновенные и десятичные дроби возникли в разное время: первые являются более древними.

Пришли из глубины веков

Впервые оперировать дробями начали на территории Египта и Вавилона. Подход математиков двух государств имел значительные отличия. Однако начало и там и там было положено одинаково. Первой дробью стала половина или 1/2. Дальше возникла четверть, треть и так далее. Согласно данным археологических раскопок, история возникновения дробей насчитывает около 5 тысяч лет. Впервые доли числа встречаются в египетских папирусах и на вавилонских глиняных табличках.

Древний Египет

Виды обыкновенных дробей сегодня включают в себя и так называемые египетские. Они представляют собой сумму нескольких слагаемых вида 1/n. Числитель — всегда единица, а знаменатель — натуральное число. Появились такие дроби, как ни трудно догадаться, в древнем Египте. При расчетах все доли старались записывать в виде таких сумм (например, 1/2 + 1/4 + 1/8). Отдельными обозначениями обладали только дроби 2/3 и 3/4, остальные разбивались на слагаемые. Существовали специальные таблицы, в которых доли числа представлялись в виде суммы.

Наиболее древнее из известных упоминаний такой системы встречается в Математическом папирусе Ринда, датируемом началом второго тысячелетия до нашей эры. Он включает таблицу дробей и математические задачи с решениями и ответами, представленными в виде сумм дробей. Египтяне умели складывать, делить и умножать доли числа. Дроби в долине Нила записывались с помощью иероглифов.

Представление доли числа в виде суммы слагаемых вида 1/n, характерное для древнего Египта, использовалось математиками не только этой страны. Вплоть до Средних веков египетские дроби применялись на территории Греции и других государств.

Развитие математики в Вавилоне

Иначе выглядела математика в Вавилонском царстве. История возникновения дробей здесь напрямую связана с особенностями системы счисления, доставшейся древнему государству в наследство от предшественника, шумеро-аккадской цивилизации. Расчетная техника в Вавилоне была удобнее и совершеннее, чем в Египте. Математика в этой стране решала гораздо больший круг задач.

Судить о достижениях вавилонян сегодня можно по сохранившимся глиняным табличкам, заполненным клинописью. Благодаря особенностям материала они дошли до нас в большом количестве. По мнению некоторых ученых, математики в Вавилоне раньше Пифагора открыли известную теорему, что, несомненно, свидетельствует о развитии науки в этом древнем государстве.

Дроби: история дробей в Вавилоне

Система счисления в Вавилоне была шестидесятеричной. Каждый новый разряд отличался от предыдущего на 60. Такая система сохранилась в современном мире для обозначения времени и величин углов. Дроби также были шестидесятеричными. Для записи использовали специальные значки. Как и в Египте, примеры с дробями содержали отдельные символы для обозначения 1/2, 1/3 и 2/3.

Вавилонская система не исчезла вместе с государством. Дробями, написанными в 60-тиричной системе, пользовались античные и арабские астрономы и математики.

Древняя Греция

История обыкновенных дробей мало чем обогатилась в древней Греции. Жители Эллады считали, что математика должна оперировать лишь целыми числами. Поэтому выражения с дробями на страницах древнегреческих трактатов практически не встречались. Однако определенный вклад в этот раздел математики внесли пифагорейцы. Они понимали дроби как отношения или пропорции, а единицу считали также неделимой. Пифагор с учениками построил общую теорию дробей, научился проводить все четыре арифметические операции, а также сравнение дробей путем приведения их к общему знаменателю.

Священная римская империя

Римская система дробей была связана с мерой веса, называемой «асс». Она делилась на 12 долей. 1/12 асса называлась унцией. Для обозначения дробей существовало 18 названий. Приведем некоторые из них:

• семис — половина асса;

• секстанте — шестая доля асса;

• семиунция — пол-унции или 1/24 асса.

Неудобство такой системы заключалось в невозможности представить число в виде дроби со знаменателем 10 или 100. Римские математики преодолели трудность с помощью использования процентов.

Написание обыкновенных дробей

В Античности дроби уже писали знакомым нам образом: одно число над другим. Однако было одно существенное отличие. Числитель располагался под знаменателем. Впервые так писать дроби начали в древней Индии. Современный нам способ стали использовать арабы. Но никто из названных народов не применял горизонтальную черту для разделения числителя и знаменателя. Впервые она появляется в трудах Леонардо Пизанского, более известного как Фибоначчи, в 1202 году.

Китай

Если история возникновения обыкновенных дробей началась в Египте, то десятичные впервые появились в Китае. В Поднебесной империи их стали использовать примерно с III века до нашей эры. История десятичных дробей началась с китайского математика Лю Хуэя, предложившего использовать их при извлечении квадратных корней.

В III веке нашей эры десятичные дроби в Китае стали применяться при расчете веса и объема. Постепенно они все глубже начали проникать в математику. В Европе, однако, десятичные дроби стали использоваться гораздо позже.

Аль-Каши из Самарканда

Независимо от китайских предшественников десятичные дроби открыл астроном аль-Каши из древнего города Самарканда. Жил и трудился он в XV веке. Свою теорию ученый изложил в трактате «Ключ к арифметике», увидевшем свет в 1427 году. Аль-Каши предложил использовать новую форму записи дробей. И целая, и дробная часть теперь писались в одной строке. Для их разделения самаркандский астроном не использовал запятую. Он писал целое число и дробную часть разными цветами, используя черные и красные чернила. Иногда для разделения аль-Каши также применял вертикальную черту.

Десятичные дроби в Европе

Новый вид дробей начал появляться в трудах европейских математиков с XIII века. Нужно заметить, что с трудами аль-Каши, как и с изобретением китайцев они знакомы не были. Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Франсуа Виет. Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта.

Однако это были лишь частные случаи научного использования. Для решения повседневных задач десятичные дроби в Европе стали применяться несколько позже. Произошло это благодаря голландскому ученому Симону Стевину в конце XVI века. Он издал математический труд «Десятая» в 1585 году. В нем ученый изложил теорию использования десятичных дробей в арифметике, в денежной системе и для определения мер и весов.

Точка, точка, запятая

Стевин также не пользовался запятой. Он отделял две части дроби при помощи нуля, обведенного в круг.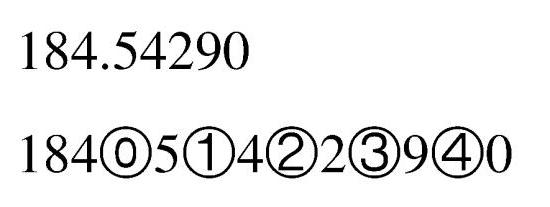 Впервые запятая разделила две части десятичной дроби только в 1592 году. В Англии, однако, вместо нее стали применять точку. На территории США до сих пор десятичные дроби пишут именно таким образом.

Одним из инициаторов использования обоих знаков препинания для разделения целой и дробной части был шотландский математик Джон Непер. Он высказал свое предложение в 1616-1617 гг. Запятой пользовался и немецкий ученый Иоганн Кеплер.

Дроби на Руси

На русской земле первым математиком, изложившим деление целого на части, стал новгородский монах Кирик. В 1136 году он написал труд, в котором изложил метод «счисления лет». Кирик занимался вопросами хронологии и календаря. В своем труде он привел в том числе и деление часа на части: пятые, двадцать пятые и так далее доли.

Деление целого на части применялось при расчете размера налога в XV-XVII веках. Использовались операции сложения, вычитания, деления и умножения с дробными частями.

Само слово «дробь» появилось на Руси в VIII веке. Оно произошло от глагола «дробить, разделять на части». Для названия дробей наши предки использовали специальные слова. Например, 1/2 обозначалась как половина или полтина, 1/4 — четь, 1/8 — полчеть, 1/16 — полполчеть и так далее.

Полная теория дробей, мало чем отличающаяся от современной, была изложена в первом учебнике по арифметике, написанном в 1701 году Леонтием Филипповичем Магницким. «Арифметика» состояла из нескольких частей. О дробях подробно автор рассказывает в разделе «О числах ломаных или с долями». Магницкий приводит операции с «ломанными» числами, разные их обозначения.

Сегодня по-прежнему в числе самых сложных разделов математики называются дроби. История дробей также не была простой. Разные народы иногда независимо друг от друга, а иногда заимствуя опыт предшественников, пришли к необходимости введения, освоения и применения долей числа. Всегда учение о дробях вырастало из практических наблюдений и благодаря насущным проблемам. Необходимо было делить хлеб, размечать равные участки земли, высчитывать налоги, измерять время и так далее. Особенности применения дробей и математических операций с ними зависели от системы счисления в государстве и от общего уровня развития математики. Так или иначе, преодолев не одну тысячу лет, раздел алгебры, посвященный долям чисел, сформировался, развился и с успехом используется сегодня для самых разных нужд как практического характера, так и теоретического.

fb.ru

Презентация "Возникновение и равитие дробей в Древнем мире".

Слайд 1

Слайд 2

В древнем Египте архитектура достигла высокого развития. Об этом свидетельствуют сохранившиеся до наших дней египетские пирамиды. Разумеется, для того чтобы строить их, чтобы вычислить длины, площади и объёмы фигур, необходимо было знать арифметику. Древний Египет.

Слайд 3

Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела. Древнеегипетские вычислители почему-то питали особое пристрастие к дробям, в числителе которых стоит единица. Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда ) — древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э. писцом по имени Ахмес на свиток папируса длиной 5,25 м. и шириной 33 см.

Слайд 4

Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали 1/4 , 1/8 ,1/16.. затем и 1/3 ,1/6 …и т.д., то есть самые простые дроби, доли целого, называемые единичными или основными дробями, в последствии их стали называть аликвотными дробями. У них числитель всегда единица. Египтяне выражали любую дробь в виде суммы только основных дробей. Всякую другую дробь египтяне представляли как сумму аликвотных дробей например: 9 / 16= 1 /2 +1 / 16;7 / 8= 1 / 2 + 1 / 4 + 1/8 и т.д. Примеры изображения часто встречающихся дробей 1 /2 1/3 2/3 1/4 1/5

Слайд 5

Самыми важными расчетами для египтянина были те, в которых применялись деление и умножение, причем деление представляло большие сложности. Для того чтобы ускорить процесс деления, египтяне составляли таблицы, в которых записывались серии ре- дробей, где число 2 делилось на все нечетные числа до 101.

Слайд 6

Итак, мы охарактеризовали основные особенности египетского способа вычислений. Знание действий умножения и деления было вполне достаточно, чтобы решить любую проблему, возникавшую при сооружении храма, пирамиды или стены, и для измерения веса использованного при этом материала. Конец.

Слайд 7

Вавилон

Слайд 8

Около 4 тысяч лет назад в Месопотамию – долину между Тигром и Ефратом на территории нынешнего Ирака – пришли два кочевых народа: сумерийцы и аккадяне. Через два века они слились в одно мощное государство – Вавилон. Ко времени слияния каждый из этих народов имел свои весовые и денежные единицы. Основной единицей у сумерийцев была «мина», а у аккадян – «шекель». «Шекель» была приблизительно в 60 раз меньше «мины». Следующей весовой единицей установили «талант», она была в 60 раз больше «мины». Происхождение шестидесятеричной системы счисления у вавилонян связано, как полагают ученые, с тем, что вавилонская денежная и весовая единицы измерения подразделялись в силу исторических условий на 60 равных частей: 1 талант = 60 мин; 1 мина = 60 шекель Во время разливов Тигра и Евфрата землю Междуречья покрывал плодородный ил. Вавилоняне, как и жители Египта, тоже были земле­дельцами. Только им приходилось труднее, чем египтянам. Тигр и Евфрат разливаются очень бурно. Для защиты от наводнений приходилось строить дамбы, обносить поля.

Слайд 9

В древнем Вавилоне высокий уровень культуры был достигнут ещё в третьем тысячелетии до н.э. там писали не на папирусе, а на глине. Путём нажима клиновидной палочкой на мягкие глиняные плитки наносились чёрточки, имевшие вид клиньев. Вот почему такое письмо называлось клинописью. Плитки сушились на знойном солнце и приобретали прочность. Получались прочные кирпичные «документы»; некоторые из них сохранились и до нашего времени. Учёные нашли при раскопках немало кирпичных актов, государственных и торговых договоров, даже учебников. Раскопками, проведенными в ХХ веке среди развалин древних городов южной части Двуречья, обнаружено большое количество клинописных математических табличек. Ученые, изучая их, установили, что за 2000 лет до н. э. у вавилонян математика достигла высокого уровня развития.

Слайд 10

Сначала писали число це­лых единиц. На втором месте — число шестидесятых долей, на третьем — шестидесятые доли от предыдущих, и так далее. Вавилоняне умели записывать любые дроби. Египтяне этого делать не умели. Изображение вавилонских дробей Система записи, применявшаяся в Вавилоне, была более экономной. Числа от 1 до 59 писались примерно так же, как и в Египте: единица обозначалась клином , а десяток — знаком , составленным из двух косых клиньев. А дальше вавилоняне поступали почти так же, как это делаем сейчас мы. Чтобы написать, например, число 205, то есть 3 * 60 + 25, они изображали . Первые три клина означали, что три раза берется единица высшего разряда (то есть 3 раза по 60), а дальше шло обозначение 25. Вавилоняне приняли за основу системы счисления число 60. Но вавилоняне долгое время не знали нуля! Поэтому вавилонским писцам было трудно разбираться ,какое именно число записано.

Слайд 11

Следы вавилонской шестидесятеричной системы счисления удержались и в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60минут, минуты на 60секунд; окружности на 360 градусов . Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии всех народов до 17 века. В отличии от них, дроби общего вида , которыми пользуемся мы, были названы обыкновенными. Что сохранилось до наших дней:

Слайд 12

Дроби в Древнем Риме.

Слайд 13

Интересная система дробей была в Древнем Риме. Римляне пользовались, в основном, только конкретными дробями, которые заменяли части известных величин. Они остановили свое внимание на мере «асс». Медную монету, а впоследствии единицу веса – асс, римляне делили на двенадцать равных частей - унций. Интересная система дробей. Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12.

Слайд 14

Путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги.

nsportal.ru

Дроби в древнем египте древнем риме

schoolfiles.net

Презентация - Дроби в Вавилоне, Риме, Египте

Слайды и текст этой презентации

Слайд 1

Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей ПРЕЗЕНТАЦИЯ ДЛЯ ИСПОЛЬЗОВАНИЯ В КАЧЕСТВЕ НАГЛЯДНОГО ПОСОБИЯ ВО ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИМаркелова Г.В., учитель математики Гремячинского филиала МБОУ СОШ с. Ключи

Слайд 2

ОГЛАВЛЕНИЕ- Из истории возникновения обыкновенных дробей: - Дроби в Вавилоне; - Дроби в Древнем Египте; - Дроби в Древнем Риме. - Открытие десятичных дробей.

Слайд 3

О происхождении дробей Необходимость в дробных числах возникла в результате практической деятельности человека. Потребность в нахождении долей единицы появилась  у наших предков при дележе добычи после охоты. Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения.   Так возникли дроби.

Слайд 4

Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей. В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.

Слайд 5

В истории развития дробного числа  мы встречаем дроби трёх видов: 1) доли или единичные дроби, у которых числитель единица, знаменателем же может быть любое целое число; 2) дроби систематические, у которых числителями могут быть любые числа, знаменателями же – только числа некоторого частного вида, например степени десяти или шестидесяти; 3) дроби общего вида, у которых числители и знаменатели могут быть любыми числами. Изобретение этих трёх различных видов дробей представляло для человечества разные степени трудности, поэтому разные виды дробей появлялись в разные эпохи.

Слайд 6

Дроби в Вавилоне Вавилоняне пользовались всего двумя цифрами. Вертикальная черточка обозначала одну единицу, а угол из двух лежащих черточек – десять. Эти черточки у них получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали.

Слайд 7

Дроби в Древнем Египте     В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику. Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.

Слайд 8

Шестидесятиричные дробиВ древнем Вавилоне предпочитали постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями. Вместо слов «шестидесятые доли», «три тысячи шестисотые доли» говорили короче: «первые малые доли», «вторые малые доли». От этого и произошли наши слова «минута» (по латыни «меньшая») и «секунда» (по латыни «вторая»). Так что вавилонский способ обозначения дробей сохранил своё значение до сих пор.

Слайд 9

«Египетские дроби» В Древнем Египте некоторые дроби имели свои особые названия – а именно, часто возникающие на практике 1/2, 1/3, 2/3, 1/4, 3/4, 1/6 и 1/8. Кроме того, египтяне умели оперировать с так называемыми аликвотными дробями (от лат. aliquot – несколько) типа 1/n – их поэтому иногда также называют «египетскими»; эти дроби имели свое написание: вытянутый горизонтальный овальчик и под ним обозначение знаменателя. Остальные дроби они записывали в виде суммы долей. Дробь 7/8 записывали в виде долей: ½+1/4+1/8.

Слайд 10

Дроби в Древнем РимеИнтересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью - весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.  1 тройская унция золота — мера веса драгоценных металлов

Слайд 11

Открытие десятичных дробей Уже несколько тысячелетий человечество пользуется дробными числами, а вот записывать их удобными десятичными знаками оно додумалось значительно позже. Сегодня мы пользуемся десятичными дробями естественно и свободно. В Западной Европе 16 в. вместе с широко распространённой десятичной системой представления целых чисел в расчётах повсюду применялись шестидесятеричные дроби, восходящие ещё к древней традиции вавилонян.

Слайд 12

Понадобился светлый ум нидерландского математика Симона Стевина, чтобы привести запись и целых, и дробных чисел в единую систему.

Слайд 13

Применение десятичных дробей С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. В Англии в качестве знака, отделяющего целую часть от дробной, была введена точка. Запятая, как и точка, в качестве разделительного знака была предложена в 1617 году математиком Непером. намного чаще, чем обыкновенные дроби. Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.

Слайд 14

Применение десятичных дробейС начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. В Англии в качестве знака, отделяющего целую часть от дробной, была введена точка. Запятая, как и точка, в качестве разделительного знака была предложена в 1617 году математиком Непером. Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.

Слайд 15

Список источниковМ.Я.Выгодский «Арифметика и алгебра в Древнем мире». Г.И.Глейзер «История математики в школе». И.Я.Депман «История арифметики». Виленкин Н.Я. « Из истории дробей» Фридман Л.М. «Изучаем математику». Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей... prezentacii.com›История›Открытие десятичных дробей ...математике "Дроби в Вавилоне, Египте, Риме. Открытие десятичных... ppt4web.ru›…drobi…rime…desjatichnykh-drobejj.html Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей"...powerpt.ru›…drobi-v…rime…desyatichnyh-drobey.html Египте, Древнем Риме, Вавилоне. Открытие десятичных дробей."... uchportal.ru›Методические разработки›Открытие десятичных дробей. История математики: ...Риме, Вавилоне. Открытие десятичных дробей... rusedu.ru›detail_23107.html 9Презентация: ...Древнем Риме, Вавилоне. Открытие десятичных дробей... prezentacii-powerpoint.ru›…drobi…vavilone…drobej/ Дроби в вавилоне, египте, риме. открытие десятичных... prezentacia.ucoz.ru›…drobi_v…desjatichnykh_drobej…

Слайд 16

Спасибо за внимание

lusana.ru

Дроби в древнем риме | Образовательный портал EduContest.Net — библиотека учебно-методических материалов

Творческая работа по математикеДроби в Древнем Риме

Работу выполнилаСазанова Татьяна, ученица 6 классаМОУ Лесогорская СОШ

РуководительЖилова Зоя Геннадьевна, учитель математики МОУ Лесогосркая СОШ

Адрес:607710, Нижегородская обл., Шатковский р-н, п. Лесогорск, ул. Электриков, д. 8.

E-mail – [email protected]Тел. 8-831-90-4-60-80

2012г.

Введение.

На уроках математики при изучении темы «Обыкновенные дроби» мы узнали некоторые исторические факты из появления и развития дробей. Мне захотелось рассмотреть этот вопрос более основательно: рассмотреть более подробно этапы развития обыкновенных дробей; найти задачи с дробями, составленные в далёком прошлом. Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни. Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе. Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения. Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.

Дроби в древнем Риме.Интересная система дробей была в Древнем Риме. У римлян основной единицей измерения массы служил асс, а также и денежной единицей. Асс делился на 12 равных частей – унций. Со временем унции стали применять для измерения любых величин. Например, римлянин мог сказать, что он

educontest.net

• 
  Древний китай известные правители
• 
  Благотворительность в древней руси
• 
  Новиков текст город древний
• 
  Поговорки с древними мерами
• 
  Древний египет в лувре
• 
  Герой древней греции персей
• 
  Мифы разных народов древние
• 
  Налоговая реформа древней руси
• 
  Древние государства западной азии
• 
  Водяные часы древнего египта
• 
  Ветеринария в древнем риме