Возникновение геометричесих понятий в древнем Египте и Вавилоне. Древний египет геометрия

Геометрия древнего Египта Введение

Геометрия древнего Египта Введение. Определение сторон горизонта. В древнейшие времена египтяне, приступая к постройке пирамиды, дворца или обыкновенного дома, сначала отмечали направление сторон горизонта (это очень важно, так как освещенность в строении зависит от положения его окон и дверей по отношению к солнцу). Действовали они следующим образом. Для того чтобы найти направление север - юг, втыкали вертикально палку и следили за ее тенью. Она становилась наименьшей, когда ее конец указывал на север. 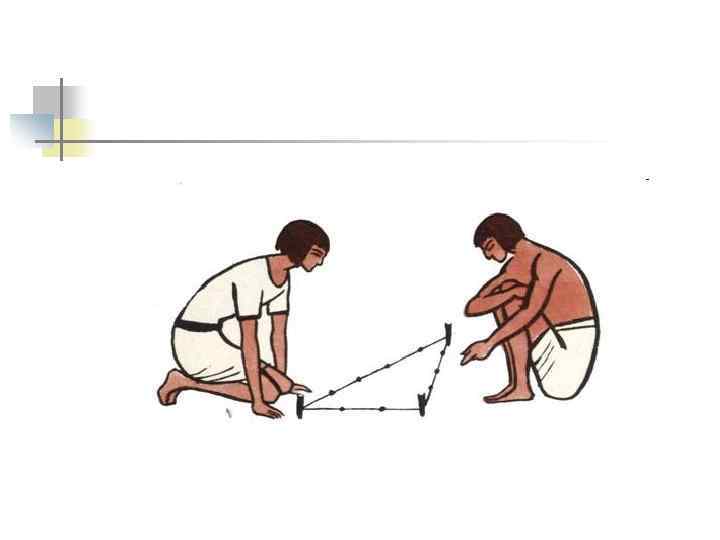Меры длины древних египтян. Измерения. В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, их называли "натягивателями веревки" - гарпетонаптами. Они брали длинную веревку, делили ее узелками (расстояние между ними равно одному локтю фараона) на двенадцать частей, а концы ее связывали. В направлении север-юг строители устанавливали два колышка на расстоянии четырех частей, отмеченных на веревке. Затем при помощи третьего колышка натягивали ее так, чтобы образовался треугольник, у которого одна сторона имела 3 части, другая 4, а третья - 5. Получался прямоугольный треугольник, площадь которого принимали за эталон, если пользовались одной и той же веревкой. При этом сторона, имеющая три части, указывала восточно-западное направление. Египетский треугольник. Вычисление площадей. Но мы теперь знаем, что египетский треугольник основан на доказанном гораздо позднее утверждении, являющимся обратным теореме Пифагора(последняя была "открыта" через много веков после того, как ею научился пользоваться обыкновенный египетский мастеровой). Египетская геометрия была практической; в ней не столько рассуждали, сколько интуитивно устанавливали правила действий, удобные для приложений, но никогда их не исследовали. Уже 4 - 5 тысяч лет назад египтяне правильно вычисляли площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция. Квадрат служил эталоном при измерении площадей благодаря своему совершенному виду. Вычисление площадей. После каждого разлива Нила египтянам заново приходилось разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площади различных фигур: ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараонов, которые собирали с земледельцев налоги. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку, разделенную метками на локти, ладони и пальцы. Если участок земли квадратный или прямоугольный, то это дело несложное. Надо измерить длину и ширину поля, а потом их перемножить. Например, длина десять локтей, а ширина восемь. Значит, на этом участке можно уложить 80 квадратов со стороной в локоть. Его площадь — восемьдесят квадратных локтей. Но участки могут иметь разную форму. Не всякий участок можно разделить на прямоугольники. А вот на треугольники можно разбить любой участок,— если только он ограничен прямыми линиями. Папирус Ахмеса Папирус Ахмеса был обнаружен в 1858 году. В 1870 он был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музее в Лондоне, а вторая часть — в Нью-Йорке. Он представляет собой собрание решений 84 задач, имеющих прикладной характер; эти задачи относятся к действиям с дробями, определению площади прямоугольника, треугольника, трапеции и круга, объёма прямоугольного параллелепипеда и цилиндра; имеются также арифметические задачи на пропорциональное деление, определение соотношений между количеством зерна и получающегося из него хлеба или пива; решение одной задачи приводится к вычислению суммы геометрической прогрессии. Однако для решения этих задач не даётся никаких общих правил, не говоря уже о попытках каких-нибудь теоретических обобщений. Интересные факты. Погребальная камера отца фараона Рамзеса II (около 1300 год до н.э.), оставшаяся недостроенной, дает представление о том, как египтяне украшали внутренние стены. Они переносили рисунок при помощи деления стены на квадратики. Таким методом сейчас широко пользуются художники для переноса изображения. Интересные факты.

Геометрия древнего Египта Выполнили ученики 10 а класса

Геометрия древнего Египта Выполнили ученики 10 а класса Чигадаев Игорь Кельбина Ирина.

Введение. Геометрия, как и всякая наука, возникла под влиянием жизненных потребностей. Необходимость их повседневного удовлетворения ставит человека перед целым рядом вопросов о форме окружающих его предметов, вычислениях, связанных с землемерием, строительным делом и т. д. Слово "геометрия" означает "землемерие" и ясно указывает на источник его происхождения. Греческие писатели единодушно сходятся на том, что геометрия возникла в Египте и оттуда перенесена в Элладу. Имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры. Узкая плодородная полоса земли между пустыней и рекой Нилом ежегодно подвергалась затоплению, и каждый разлив смывал границы участков, принадлежавших отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко. Это заставило египтян заниматься вопросами измерения, то есть землемерием. Помимо этого, они вели развитую торговлю и поэтому нуждались в умении измерять емкость сосудов. Искусство кораблевождения привело их к астрономическим сведениям. Выдающиеся постройки египтян - пирамиды, которые сохранились до нашего времени, свидетельствуют, что их сооружение требовало знания пространственных форм. Все это указывает на чисто опытное происхождение геометрии.

Меры длины древних египтян. Главной мерой длины у египтян служил локоть. Локоть делился на семь «ладоней» , «ладонь» — на четыре «пальца» . Как и многие другие народы, в качестве мерок длины египтяне использовали части человеческого тела. Но люди бывают разного роста, и локти у них не одинаковые. Египтяне это, конечно, понимали. Для того чтобы измерения получались точными и не происходило никакой путаницы, они придумали образцовые меры: локоть, ладонь и палец, общие для всего Египта. Теперь было уже неважно, какой длины руки у человека, который хотел что-нибудь измерить. Он мерил не своим, а «общим» локтем, а именно фараона.

Измерения. В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, их называли "натягивателями веревки" - гарпетонаптами. Они брали длинную веревку, делили ее узелками (расстояние между ними равно одному локтю фараона) на двенадцать частей, а концы ее связывали. В направлении север-юг строители устанавливали два колышка на расстоянии четырех частей, отмеченных на веревке. Затем при помощи третьего колышка натягивали ее так, чтобы образовался треугольник, у которого одна сторона имела 3 части, другая 4, а третья - 5. Получался прямоугольный треугольник, площадь которого принимали за эталон, если пользовались одной и той же веревкой. При этом сторона, имеющая три части, указывала восточно-западное направление.

Египетский треугольник с соотношением сторон 3: 4: 5 активно применялся для построения прямых углов землемерами и архитекторами. Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры -катеты являлись направляющими для кладки прямого угла сооружения. В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности.

Вычисление площадей. Но мы теперь знаем, что египетский треугольник основан на доказанном гораздо позднее утверждении, являющимся обратным теореме Пифагора(последняя была "открыта" через много веков после того, как ею научился пользоваться обыкновенный египетский мастеровой). Египетская геометрия была практической; в ней не столько рассуждали, сколько интуитивно устанавливали правила действий, удобные для приложений, но никогда их не исследовали. Уже 4 - 5 тысяч лет назад египтяне правильно вычисляли площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция. Квадрат служил эталоном при измерении площадей благодаря своему совершенному виду.

Вычисление площадей. После каждого разлива Нила египтянам заново приходилось разбивать поля на участки, находить их границы. А для этого надо было уметь измерять площади различных фигур: ведь поле может иметь какую угодно форму. Особенно тщательно поля измеряли чиновники фараонов, которые собирали с земледельцев налоги. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку, разделенную метками на локти, ладони и пальцы. Если участок земли квадратный или прямоугольный, то это дело несложное. Надо измерить длину и ширину поля, а потом их перемножить. Например, длина десять локтей, а ширина восемь. Значит, на этом участке можно уложить 80 квадратов со стороной в локоть. Его площадь — восемьдесят квадратных локтей. Но участки могут иметь разную форму. Не всякий участок можно разделить на прямоугольники. А вот на треугольники можно разбить любой участок, — если только он ограничен прямыми линиями.

Деление участка на треугольники.

Папирус Ахмеса был обнаружен в 1858 году. В 1870 он был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музее в Лондоне, а вторая часть — в Нью-Йорке. Он представляет собой собрание решений 84 задач, имеющих прикладной характер; эти задачи относятся к действиям с дробями, определению площади прямоугольника, треугольника, трапеции и круга, объёма прямоугольного параллелепипеда и цилиндра; имеются также арифметические задачи на пропорциональное деление, определение соотношений между количеством зерна и получающегося из него хлеба или пива; решение одной задачи приводится к вычислению суммы геометрической прогрессии. Однако для решения этих задач не даётся никаких общих правил, не говоря уже о попытках каких-нибудь теоретических обобщений.

Часть папируса Ахмеса

Интересные факты. n Погребальная камера отца фараона Рамзеса II (около 1300 год до н. э. ), оставшаяся недостроенной, дает представление о том, как египтяне украшали внутренние стены. Они переносили рисунок при помощи деления стены на квадратики. Таким методом сейчас широко пользуются художники для переноса изображения. Данный факт подтверждает то, что им были знакомы элементарные свойства подобных фигур и зачатки теории пропорций. n

Разделение рисунка на квадратики

Интересные факты. Сохранилось немало планов земельных угодий, разделенных на участки прямоугольной, трапецеидальной или треугольной форм. Прямоугольник египтяне называли "то, что имеет длину и ширину", трапецию - "лбом быка", сегмент - "полем полумесяца", параллельные прямые - "двойными прямыми". У них не было таких геометрических понятий как точка, прямая, линия, поверхность, плоскость, параллельность. Измерение производилось при помощи веревки.

Используемые ссылки. n n n http: //isgeom. narod. ru/index. html (История элементарной геометрии) http: //ru. wikipedia. org/wiki/Заглавная_страница (Википедия) http: //revolution. allbest. ru/mathematics/00003120_0. html http: //www. nntu. sci-nnov. ru/lib/resyrs/student_kyltyralog/1. htm (Искусство древних цивилизаций) http: //oldegypt. info/index. php? p=product http: //www. krugosvet. ru/enc/nauka_i_tehnika/matematika/GEOMETRIY A. html

present5.com

Геометрия в Древнем Египте

Геометрия в Древнем Египте (теория)

Выполнили: Титаренко М.А.,

Жукова Е.Е.

• Слово «геометрия» составлено из двух древнегреческих слов: GE - «Земля» и metreo - «измеряю». Первый период развития геометрии протекал в Древнем Египте, примерно до 5 века до н. э. 

• Древний Египет считается первым государством, оставившим самые ранние математические тексты. Древние греки, достижения которых лежат в основе современной науки, считали себя учениками египтян.

Геродот писал:

• «Египетские жрецы говорили, что царь разделил землю между всеми египтянами, дав каждому по равному прямоугольному участку; из этого он создал себе доходы, приказав ежегодно вносить налог. Если же река отнимала что-нибудь, то царь посылал людей, которые должны измерить участок и уменьшить налог».

• Первой книгой, содержащей геометрические задачи, считается папирус Райнда, который датируется 19 веком до нашей эры. 

Что умели древние египтяне: 

• Умели точно находить площадь поля прямоугольной, треугольной, трапециевидной формы.
• Умели строить прямоугольный треугольник при помощи верёвки, разделённой узлами на 12 равных частей.
• Знали, что отношение длинны окружности к диаметру- число постоянное, приближённое значение этого числа- П.
• Среди пространственных тел самым египетским можно считать пирамиду, ведь именно такую форму имеют знаменитые усыпальницы фараонов, хотя довольно близко они знакомы с кубом, параллелепипедом, призмой и цилиндром, умели вычислять объём этих фигур.
• Умели вычислять объём усечённой пирамиды, в основании которой квадрат. 

V прям. параллелепипеда = S * h

• V – объём
• S – площадь основания
• h – высота

S круга = (8/9 d)2 = 64/81d2

• d – круга диаметр

V = 1/6aS

• S - площадь грани куба
• а – сторона куба

1/6aS = 1/3 а/2 S

• h = а/2 – высота пирамиды
• S – площадь основания пирамиды

V = 1/3 h S

• V – объём пирамиды 

• Геометрия – одна из самых древних наук, её возраст исчисляется тысячелетиями. В геометрии много формул, задач, теорем, фигур, аксиом. 

Геометрия в Древнем Египте (теория)

Спасибо за внимание!

Выполнили: Титаренко М.А.,

Жукова Е.Е.

multiurok.ru

Возникновение геометричесих понятий в древнем Египте и Вавилоне

В древнейшие времена египтяне, приступая к постройке пирамиды, дворца или обыкновенного дома, сначала отмечали направление сторон горизонта (это очень важно, так как освещенность в строении зависит от положения его окон и дверей по отношению к солнцу). Действовали они следующим образом. Для того чтобы найти направление север - юг, втыкали вертикально палку и следили за ее тенью. Она становилась наименьшей, когда ее конец указывал на север.

В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон.

Занимались измерениями особые специалисты, их называли "натягивателями веревки" - гарпетонаптами. Они брали длинную веревку, делили ее узелками (расстояние между ними равно одному локтю фараона) на двенадцать частей, а концы ее связывали. В направлении север-юг строители устанавливали два колышка на расстоянии четырех частей, отмеченных на веревке. Затем при помощи третьего колышка натягивали ее так, чтобы образовался треугольник, у которого одна сторона имела три части, другая четыре, а третья - пять. Получался прямоугольный треугольник, площадь которого принимали за эталон, если пользовались одной и той же веревкой. При этом сторона, имеющая три части, указывала восточно-западное направление. Вряд ли египетские строители осознавали, что их метод нуждался в каком-либо обосновании.

Но мы теперь знаем, что он основан на доказанном гораздо позднее утверждении, являющимся обратным теореме Пифагора. А последняя была "открыта" через много веков после того, как ею научился пользоваться обыкновенный древнеегипетский мастеровой. Египетская геометрия была практической; в ней не столько рассуждали, сколько интуитивно устанавливали правила действий, удобные для приложений, но никогда их не исследовали. Египтяне правильно вычисляли площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция: основание треугольника делилось пополам и умножалось на высоту.

Погребальная камера отца фараона Рамзеса II (около 1300 год до н.э.), оставшаяся недостроенной, дает представление о том, как египтяне украшали внутренние стены. Они переносили рисунок при помощи деления стены на квадратики. Таким методом сейчас широко пользуются художники для переноса изображения. Данный факт подтверждает то, что им были знакомы элементарные свойства подобныx фигур и зачатки теории пропорций.

Как видим, в древнем Египте перед писцами в основном стояли практические проблемы. Многие решения находились путем проб, эмпирически. На наряду с этим в начале II тысячелетия до нашей эры шла интенсивная работа творческой мысли, задачи мысленно обобщались и принимали более абстрактный характер. В начале XX века в результате археологических раскопок, проводившихся между реками Тигром и Ефратом, там, где когда-то процветало государство Вавилон, было обнаружено несколько сотен глиняных табличек. Около трехсот из них относятся к математике и датируются либо временем первой вавилонской династии Хаммурапи (с 1894 по 1595 гг. до н.э.), либо периодом эпохи Селевкидов (VI-III в.в. до н.э.). На табличках встречаются последовательности чисел, геометрические соотношения и задачи. Математические познания вавилонян применялись при денежном и товарном обмене, в задачах на простые и сложные проценты, при вычислении налогов и распределении урожая. Большинство задач можно отнести к разряду хозяйственных. Хотя характер вавилонской математики был в основном алгебраическим, происхождение задач, записанных писцами, было часто геометрическим, например, вычисление площадей, объемов некоторых простых фигур и тел. Уже 4 - 5 тысяч лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат служил эталоном при измерении площадей благодаря своему совершенному виду. Но геометрическая форма задачи обычно являлась только средством для того, чтобы поставить алгебраический вопрос.

К задачам, которые вавилоняне решали алгебраическим и арифметическим методом, относятся и многие задания на определение длин, площадей при делении земельных участков, объемов земляных выемок, хозяйственных построек. Все решения, встречающиеся в клинописных текстах, ограничиваются простым перечислением этапов вычисления в виде догматических правил: "делай то - то, делай так - то". В дошедших до нас вавилонских табличках имеются задачи абстрактного характера и внешне кажущиеся не связанными с практическими нуждами. Но это не так: они возникли в результате теоретической обработки условий, первоначально порожденных потребностями практики при межевании земель, возведении стен и насыпей, при строительстве каналов, плотин, оборонительных сооружений и пр. Сохранилось немало планов земельных угодий, разделенных на участки прямоугольной, трапецеидальной или треугольной форм. Но соответствующие геометрические фигуры воспринимались ими как абстрактные, так прямоугольник они называли "то, что имеет длину и ширину", трапецию - "лбом быка", сегмент - "полем полумесяца", параллельные прямые - "двойными прямыми". У вавилонян не было таких геометрических понятий как точка, прямая, линия, поверхность, плоскость, параллельность. Измерение производилось при помощи веревки. Геометрические познания вавилонян превышали египетские.

Расцвет государства Вавилон коснулся различных областей знаний. Наблюдения за небесными светилами, вызванные необходимостью путешествий по водным путям и караванными тропами, оформились у вавилонских жрецов в науку астрологию. Изучение небесных явлений позволило им создать астрономию. Они знали скорость движения Луны, продолжительность лунного месяца, периодичность солнечных и лунных затмений. Знания вавилонян оказали заметное влияние на последующее развитие математики.

isgeom.narod.ru

Геометрия у древних людей

Доклад по геометрии

_________________________________

_________________________________

Шушаковой Анны Андреевны

«История возникновения геометрии»

Москва, 2004

Содержание:

Введение стр. 3

2. Геометрия у древних: Египет и Вавилон стр. 4

3. Греция – развитие геометрии как науки стр. 5

Введение

Геометрия – одна из самых древнейших наук, она возникла очень давно, еще до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» - по-гречески земля, а «метрео» - мерить). Его можно объяснить следующими словами, приписываемыми древнегреческому учёному Евдему Родосскому (4 в. до н. э.): "Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития р. Нил, постоянно смывавшего границы".

Древнейшие из доступных нам документов позволяют предположить, что существует непосредственная связь между истоками геометрии и требованиями повседневной жизни: изготовление и украшения предметов быта, строительство жилых зданий, амбаров и погребальных памятников, вычисление площадей полей и т.д.

Геометрия у древних: Египет и Вавилон.

Геродот также возводит истоки египетской геометрии к необходимости после каждого разлива Нила заново справедливо распределять поля между их владельцами, подтверждая тем самым материальность происхождения геометрии. Египетская геометрия была практичной. В ней не столько рассуждали, сколько устанавливали правила действий, удобные для приложений, но сами эти правила никогда не исследовались. Египтяне правильно вычисляли площади некоторых прямоугольных фигур, таких как прямоугольник, квадрат, треугольник и трапеция.

При довольно примитивной и громоздкой арифметике египтяне смогли добиться значительных успехов в геометрии.

Древние египтяне были замечательными математиками и инженерами. Строительство пирамид – дело сложное и не простое даже в наше время высоких достижений, а ведь у них не было ни строительных кранов, ни домкратов. Все пирамиды имеют совершенно одинаковую правильную форму. Одна сторона пирамиды всегда обращена точно на восток, другие – север, запад, юг. Но ведь построить правильную пирамиду совсем не так просто. Даже сейчас люди учатся этому только в средней школе. А египтяне умели строить пирамиды уже пять тысяч лет назад. Некоторые секреты египетских строителей не раскрыты до сих пор.

Кроме замечательных построек – пирамид, храмов и дворцов – до нас дошли многие записи и даже большие рукописи, сделанные древними египтянами. Древнейшая математическая рукопись египтян написана около 4000 лет назад. Она хранится в Москве - в Музее изобразительных искусств имени А.С. Пушкина и называется московским папирусом. Другой математический папирус хранится в Лондоне. Написан он на 200-300 лет позднее Московского и писцом по имени Ахмес. В нем дается решение 84 задач на различные вычисления, которые могут понадобиться на практике, и некоторые довольно сложны даже для учеников старшеклассников. Задач по геометрии в нем почти нет. Но о том, что египтяне отлично для своего времени знали геометрию, рассказывают другие документы и их постройки. После каждого разлива Нила им приходилось заново разбивать поля на участки, находить их границы.

А площадь поля, как её измерить? Если участок земли квадратный или прямоугольный, то это дело несложное. Надо измерить длину и ширину поля, а потом их перемножить. Но участки могут иметь разную форму. Не всякий участок можно разделить на прямоугольники. А вот на треугольники можно разбить любой участок, - если только он ограничен прямыми линиями.

Посмотрите в учебник геометрии. В нем изучению треугольников отведено гораздо больше места, чем изучению любой другой прямолинейной фигуры. Причина этого заключается в том, что изучение других фигур основывается на знании свойств треугольников.

И египетские землемеры научились измерять площадь треугольника.

египетским математикам удалось решить и другую задачу. Они нашли

способ, хоть и приблизительно : вычислить площадь

круга по его поперечнику (диаметру).

Вавилоняне, как и жители Египта были земледельцами. Только им приходилось труднее, чем египтянам. Их государство находилось между двумя реками: Евфрат и Тигр, которые разливались очень бурно. Для защиты населения и земель от наводнений им приходилось строить дамбы, обносить поля и селения насыпями. А для строительства всяких больших сооружений нужны знания. Именно здесь, в Вавилоне было изобретено колесо, которое сыграло очень большую роль в истории Вавилона.

Не удивительно, что вавилонские ученые старательно изучали свойства окружности – колесного обода.

Прежде всего надо было научиться измерять длину окружности. Дело это не такое простое: ведь линейку с делениями к окружности приложить нельзя. Вот как приходилось поступать: Чертили окружность и два квадрата: один - так, чтобы его углы упирались в окружность изнутри, второй квадрат, побольше, вавилоняне рисовали так, чтобы окружность помещалась как раз в нем.

Получалось, что большой квадрат как бы надет на окружность и упирается в нее серединками своих сторон. Потом измеряли длину сторон большого и меньшего квадратов, - это легко сделать простой линейкой. Получившиеся числа они складывали и потом делили пополам. Считалось, что это и есть длина окружности. Конечно, это не очень точный способ, но чаще всего этого было достаточно.

Греция – развитие геометрии как науки.

Весьма большая часть нашего современного школьного курса математики, особенно геометрия, была известна древним грекам. Пожалуй, никто в истории человечества не сделал столько открытий в классической математике, сколько ученые Греции.

Настоящей наукой математика стала только у древних греков. Это был удивительный и умный народ, у которого учатся многому даже сейчас, тысячи лет спустя. Греки были отличными моряками, во всех направлениях бороздили Средиземное море. Они везли посуду и украшения из Вавилона, бронзовое оружие из Египта, шкуры зверей и хлеб с берегов Черного моря. И вместе с товарами привозили в Грецию знания. Но греки не просто учились у других народов. Они очень скоро обогнали своих учителей.

Греки считали, что спор помогает найти самое лучшее, правильное решение. Они даже изречение придумали «В споре рождается истина». И в науке греки стали поступать так же, как на народном собрании. Они не просто заучивали правила, а доискивались причины: почему правильно делать так, а не иначе.

Каждое правило греческие математики старались объяснить, доказать, что оно действительно верное. Для этого они спорили друг с другом, рассуждали, старались найти в рассуждениях ошибки. Докажут одно правило – рассуждения ведут к другому, более сложному, потом – к третьему, четвертому. Из правил складывались законы, а из законов – наука. Греческие ученые не случайно так много занимались математикой. «Математика есть ключ ко всем наукам», - говорил один из них. Другой ученый – Платон, над дверью дома, в котором он занимался со своими учениками, велел сделать такую надпись: «не обучавшийся геометрии пусть не входит в эту дверь»

В надписи Платона не случайно говорится о геометрии, а не о математике вообще. Геометрию греки считали особенно важной наукой. Греки первыми научились издали определять расстояние до корабля в море или другого недоступного предмета. Для этого они использовали свойства прямоугольного треугольника с двумя одинаковыми сторонами – равнобедренного треугольника. У такого треугольника каждый из двух одинаковых углов равен 45 градусам – половине прямого угла.

Выходит, что если мысленно построить такой прямоугольный треугольник, то расстояние по берегу от вершины прямого угла, где вбит шест, до человека с угольником как раз равно расстоянию от шеста до корабля.

Немало имен греческих математиков встречаются в учебниках арифметики и геометрии.

Самым ранним греческим математиком является Фалес (VII-VI века до н.э.).

Ему приписывается несколько начальных теорем геометрии (о равенстве углов при основании равнобедренного треугольника, о равенстве треугольников по стороне и двум прилежащим к ней углам и другие). Он предсказал солнечное затмение, сделав предварительные расчеты. Греческий математик Фалес научил египтян определять высоту пирамиды по длине ее тени.

Примерно 2200 лет назад жил знаменитый греческий ученый геометр Евклид, имя которого сейчас знает весь мир.

Все книги Евклида основываются на аксиомах – утверждениях, не требующих доказательств. Например, аксиома о точке. Вот ее формулировка: “Точка есть то, что не имеет частей и не имеет величины”.

“Начала” Евклида, законченные около 325 года до н. э., оказали значительное влияние на развитие математики вплоть до 19 века. В его 13 книгах систематически изложены существенные разделы математики, являвшиеся итогом ее развития до Евклида. Труд был построен на основе аксиом, постулатов и определений. Пожалуй, самым главным и широко изучаемым постулатом является пятый (одиннадцатая аксиома). Вот его формулировка: “Если дана прямая и точка не лежащая на ней, то можно провести только одну прямую, проходящую через точку и не пересекающуюся с данной прямой”.

Для построения фигур Евклид пользовался только линейкой и циркулем – других инструментов он не допускал. Самым важным у Евклида были рассуждения, которыми он доказывал все то, что писал. Теперь у наших математиков есть много разных инструментов и приборов, которые помогают им работать. Однако и сейчас самое важное в математике – это рассуждение и доказательство.

Математик и механик Архимед (287 – 212 годы до н.э.) считался величайшим математиком всех времен. У него имеются начала многих идей математики, к которым европейские народы пришли на 2000 лет позднее.

Циркуль- (от лат. circulus - круг), чертежный инструмент для вычерчивания окружностей и переноса размеров на чертежи. Состоит из двух шарнирно соединенных стержней, один из которых опорный (с иглой на конце), другой - измерительный (также с иглой) либо чертежный (с грифелем или рейсфедераом ).

Легенды Древней Греции утверждают, что циркуль изобрел Талос. Этот мастер приходился племянником знаменитому Дедалу, который вместе со своим сыном Икаром поднялся в небо на крыльях собственного изготовления. Вероятно, унаследовав от дяди дар изобретательства, Талос соединил два одинаковых по длине стержня и смастерил устройство способное чертить идеальный круг.

Введение

Кое-кто, возможно, считает, что различные замысловатые линии, фигуры, поверхности можно встретить только в книгах учёных-математиков. Однако, стоит осмотреться, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Оказывается их очень много. Просто мы их не всегда замечаем.

Цель моей работы - исследовать какие геометрические фигуры, тела встречаются вокруг нас.

Исходя из поставленной цели, были поставлены следующие задачи:

изучить использование геометрических форм и линий в практической деятельности человека;

изучить некоторые природные творения в виде геометрических фигур;

изучить использование геометрических фигур животными.

Методы исследования:

изучение дополнительной литературы по данному вопросу

наблюдение в повседневной жизни.

Геометрия у древних людей

Треугольники, квадраты, ромбы, окружности… каждый ученик сталкивается с ними в школе на уроках геометрии.

Научная формулировка гласит, что геометрия - это раздел математики, который изучает пространственные фигуры и формы.

Ещё в эпоху неолита люди составляли на стенах пещер орнаменты из треугольников, ромбов, прямоугольников, кругов. Древние художники тонко чувствовали красоту геометрических форм; наскальные рисунки, выполненные с большой любовью к природе, радовали глаз. (рис.1) Человек отмечал равенство, симметрию, подобие фигур. Со временем он научился использовать свойства фигур в практической жизни. Геометрия - древнейшая наука, а первые геометры производили расчеты свыше тысячи лет назад.

Земледельцы, жившие на берегах великих рек: Нила, Тигра и Ефрата, Инда и Ганга, искусно делили свои земельные участки. Для проведения замеров были выработаны первые правила новой науки - "геометрии", что в переводе с греческого и означает - "землемерие".

Геометрические фигуры интересовали наших предков не только потому, что помогали решать практические задачи. Некоторые из фигур имели для людей магическое значение. Так, треугольник считался символом жизни, смерти и возрождения; квадрат - символом стабильности. Вселенную, бесконечность обозначали правильным пятиугольником - пентагоном, правильный шестиугольник - гексагон, являлся символом красоты и гармонии. Круг - знаком совершенства.

Дата добавления: 2015-10-30; просмотров: 691 | Нарушение авторских прав

mybiblioteka.su

Геометрия древнего Египта — презентация

freedocs.xyz

Смотрите также

• 
  Сады древнего мира
• 
  Древняя война ядерная
• 
  Древний вавилон наука
• Древний мир палестина
• 
  Древние породы кошек
• 
  Самый древний философ
• 
  Самые древние акулы
• 
  Палестина древний мир
• Название древняя армения
• 
  Древние весенние праздники
• 
  Задачи древнего востока