Математика в Древнем Египте. Умножение в древнем египте
Умножение в Древнем Египте — Математика. Школьный курс. Как умножить 67 на 2. Навеяно обсуждением в математическом сообществе Facebook. Без двоичной системы напишу, хорошо? Все значки, которые использовали в Египте рисовать не буду, рассмотрим три из них: Начинаем считать. Мы берем число 67 два раза. Что это значит? Что мы два раза берем по шесть десятков и два раза по семь единиц. Итак, берем два раза по шесть значков, mariasmaths.blog Древнее египетское умножение • ru.knowledgr.com В математике древнее египетское умножение (также известный как египетское умножение, эфиопское умножение, российское умножение, или крестьянское умножение), один из двух методов умножения, используемых писцами, было систематическим методом для умножения двух чисел, который не требует таблицы умножения, только способность умножиться и разделиться на 2 и добавить. Это анализирует один из сомножителей (обычно большее) в сумму полномочий два и составляет таблицу doublings второго сомножителя. Этот метод можно назвать посредничеством и duplation, где посредничество означает делить на два одно число, и duplation означает удваивать другое число. Это все еще используется в некоторых областях. Второй египетский метод умножения и разделения был известен из культовой Москвы и Математических Папирусов Rhind, написанных в семнадцатом веке до н.э. писцом Ахмесом. Хотя в древнем Египте понятие основы 2 не существовало, алгоритм - по существу тот же самый алгоритм как долгое умножение после того, как множитель и сомножитель преобразованы в набор из двух предметов. Метод, как интерпретируется преобразованием в набор из двух предметов находится поэтому все еще в широком использовании сегодня, как осуществлено схемами двоичного умножителя в современных компьютерных процессорах. Разложение Древние египтяне выложили столы большого числа полномочий два, чтобы не быть обязанными повторно вычислить их каждый раз. Разложение числа таким образом состоит из нахождения полномочий два, которые составляют его. Египтяне знали опытным путем, что данная власть два только появится однажды в числе. Для разложения они продолжались систематически; они первоначально нашли бы самую большую власть двух меньше чем или равных рассматриваемому числу, вычли бы его и повторение, пока ничто не осталось. (Египтяне не использовали ноль числа в математике.) Чтобы найти самую большую власть 2 продолжают удваивать Ваш ответ, начинающийся с номера 1, например : Пример разложения номера 25: : Стол После разложения первого сомножителя необходимо построить стол полномочий два раза второго сомножителя (обычно меньшее) от одного до самой большой власти двух найденных во время разложения. В столе линия получена, умножив предыдущую линию два. Например, если самая большая власть двух найденных во время разложения равняется 16, и второй сомножитель равняется 7, таблица составлена следующим образом: Результат Результат получен, добавив числа из второй колонки, для которой соответствующая власть два составляет часть разложения первого сомножителя. Главное преимущество этой техники состоит в том, что она использует только дополнение, вычитание и умножение два. Пример Здесь, в реальных цифрах, то, как 238 умножен на 13. Линии умножены на два от одного до следующего. Галочка помещена полномочиями два в разложении 238. С тех пор 238 = 2 + 4 + 8 + 32 + 64 + 128, распределение умножения по дополнению дает: Российское крестьянское умножение В российском крестьянском методе полномочия два в разложении сомножителя найдены, сочиняя его слева и прогрессивно деля на два левую колонку, отказываясь от любого остатка, пока стоимость не равняется 1 (или-1, когда возможная сумма инвертирована), удваивая правильную колонку как прежде. Линии с четными числами на левой колонке вычеркиваются, и остающиеся числа справа добавлены вместе. Справочная информацияС 1880-х, как формализовано в 1920-х, неполное представление определило египетское умножение. Онлайн-энциклопедия Спрингера суммирует представление 1920-х этот путь (от Planetmath http://planetmath .org/encyclopedia/EgyptianMultiplicationAndDivision.html): Заключения 1920-х должным образом расшифровали неполную совокупную версию египетского умножения. Историки 1920-х не развили отчет 1895 года, который предположил, что вторая форма метода умножения присутствовала в RMP Ахмеса 2/n стол и RMP 36. Второй метод включал кратные части, как Спрингер предположил. О кратной части сообщил Ф. Хулч в 1895. Хулч разобрал 2/n стол Ахмеса разоблачающие кратные образцы части. Все же египетский вход энциклопедии умножения Спрингера не определял критическую кратную часть эксплуатационные детали, которые требуются, чтобы переводить информацию на современные арифметические заявления. К сожалению, математические историки 1920-х перескочили через несколько эксплуатационных деталей, такой с 1 895 кратных предметов обсуждения части Ф. Хулча, таким образом неправильно придя к заключению, что кратные образцы части не были замечены в 2/n столе Ахмеса. Кратный сюжет части остался нерешенной проблемой до 21-го века. Вскоре после 2002 Папирус Kahun и RMP 2/n стол показали две кратных части эксплуатационные методы: (1) новые обратные методы умножения и разделения, и (2) метод числа LCM, написанный красным (RMP 38). Методы умножения и разделения были кратной частью скрытого Хулча эксплуатационные шаги, включая красные вспомогательные шаги чисел, которые выбрали 'оптимизированные' делители LCM. В 2006 метод Hultsch-Мишек 1895 года был подтвержден от второго направления, детализировав общий кратный метод, используемый в RMP и египетском Математическом Кожаном Рулоне. Этот метод измерил преобразование 1/p, 1/pq, 2/p, 2/pq, n/p и n/pq рациональных чисел LCM m, письменный как m/m. Кратные шаги подразделения части Ахмеса, ощущаемые в 19-м веке, не расшифрованный в течение 20-го века, начали выпускать его тайны после 2001, все более и более к 2006 и 2009 (RMP 36). Две причины неверно направили математических историков 1920-х. Первое преждевременно закрылось, предмет египетских операций по арифметике части заключительным египетским умножением содержал только совокупные шаги. Во-вторых, scribal подразделение был предложен, следовали за необратным процессом, названным 'единственное ложное положение'. Кроме того, Спрингер следовал традиционному определению 1920-х египетского подразделения, предлагая: «Подразделение было выполнено, вычтя из числа, которое будет разделено числа, полученные последовательным удвоением делителя». Математические историки звонят, 1920-е предложили египетский метод подразделения 'единственное ложное положение'. Как ни странно, 'единственное ложное положение' было сначала зарегистрировано в 800 н. э. Более поздние арабские тексты улучшили его корень, находящий 'дважды ложное положение' метод. Определение Спрингера египетского подразделения было исторически неполным. Чтобы закончить определение египетского подразделения первые шесть проблем RMP, подразделение 10 трудовыми уровнями (определенный ранее в Папирусе Reisner) набор проблем консультируются. Кроме того, с проблемами алгебры RMP и методами консультируются. Например, Ahmes разделился 28 на 97 в RMP 31 (подтвержденный в RMP 34), решив: x + (2/3 + 1/2 + 1/7) x = 33 и x + (2/3 + 1/2 + 1/7) x = 37, поскольку другие вульгарные проблемы части были решены в Папирусе Kahun и Папирусе Rhind 2/n столы. Кратные шаги части были скрыты в теоретических операциях по умножению и разделению больше 100 лет. Ahmes не упоминал 'единственное ложное положение' в проблемах алгебры, справедливое замечание, сделанное Лотком малиновок в 1987. Неточная гипотеза 1920-х была заменена, разобрав большие вульгарные части, сняв примечание части единицы. Например, 28/97, в RMP 31 и RMP 23 выставляют LCM Ахмеса multplication метод. В RMP 23, где 45 множителей были введены, чтобы решить большую часть проблемы. Все же прочитать полную проблему LCM 360 было необходимо, поскольку другие проблемы алгебры RMP были решены. В 21-м веке Ahmes становится ясно сообщаемым, преобразовывая вульгарные части в оптимизированный ряд частей единицы в пределах метода LCM. Метод LCM также применил кратные части знаменателя, чтобы решить 2/97 в RMP 31, и в 2/n столе. Ahmes преобразовал 28/97 в две проблемы, 2/97 и 26/97, выбрав два множителя LCM, таким образом что: 1. Преобразовать 2 97: 2/n стол Ахмеса написал 2/n преобразованиям меньше, чем 2/101, он выбрал очень делимый номер m как множитель оптимизации m/m. В 2/97 случае 56 был отобран, создав множитель 56/56 таким образом, что кратные части 56 (28, 14, 8, 7, 4, 2, 1) были введены в решение, сочиняя: : 2/97 × (56/56) = 112 / (56×97) = (97 + 8 + 7) / (56×97) и, : 2/97 = 1/56 + 1/679 + 1/776 2. Чтобы преобразовать 26/97 в ряд частей единицы, Ахмес искал множитель m/m, который увеличит нумератор до большего, чем 97. Ахмес нашел 4/4. Рассматривая кратные части 4 (4, 2, 1) Ахмес выписал: : 26/97 × (4/4) = 104 / (4×97) = (97 + 4 + 2 + 1) / (4×97) таким образом, что: : 26/97 = 1/4 + 1/97 + 1/194 + 1/388 и, 3. Ahmes объединил шаги 2/97 и 26/97 в один египетский ряд частей, сочиняя: : 28/97 = 1/4 + 1/56 + 1/97 + 1/194 + 1/388 + 1/679 + 1/77 поскольку RMP 36 преобразовал 30/53 2/53 + 28/53 с 2/53, измеренным (30/30) и 28/53, измеренным (2/2). 4. Египетское умножение было обратной операцией к египетской деятельности подразделения, и наоборот. Современно выглядящие операции по умножению и разделению были скрыты в рамках египетского примечания части. Одно значение - то, что 'единственное ложное положение' представляло гипотезу 20-го века, которая исторически не прочитала совокупные нумераторы Ахмеса, написанные в проблемах умножения. Операции подразделения Ahmes, описанные кратной частью, вступают более чем 20 проблем алгебры, включите древние и современные методы подразделения как инверсия к египетскому умножению. Египетские писцы применили несколько современных теоретических идей, главным образом арифметических, как зарегистрировано в математическом ящике для инструментов Ahmes. Второе значение содержится в RMP 38. Это детализирует Ahmes, умножающий 320 ro, один hekat, к 35/11 временам 1/10 = 7/22, получая 101 + 9/11. Ahmes доказал, что 101 + 9/11 был правилен, умножившись инверсией 7/22 или 22/7. Египетское подразделение обычно применяло инверсию египетского умножения в BCE 1900 года Akhmim Wooden Tablet (AWT) и все другое Среднее Королевство математические тексты. AWT, например. разделенный один hekat, (64/64), n = 3, 7, 10, 11 и 13. Фактор и ответы остатка были умножены на инверсии делителя, 1/3, 1/7, 1/10, 1/11 и 1/13, точно возвратив начинающееся рациональное число (64/64). Наконец, красные нумераторы нумератора, подразумеваемые 2/n столом, были непосредственно обсуждены в RMP 36. Ahmes преобразовал, 2/53, 3/53, 5/53, 15/53, 28/53 и 30/53 по двум правилам. Первое правило измерило 2/53* (30/30) = 60/1590, 3/53 (20/20) = 60/1060, 5/53* (12/12) = 60/636, 15/53* (4/4) = 60/212, 28/53* (2/2) = 56/106. Второе правило преобразовало 30/53, разобрав 30/53 в 2/53 + 28/53. поскольку Ahmes преобразовал 28/97, разобрав 29/97 в 2/97 + 26/97. Заключение: Чтобы понять древнее египетское умножение и разделение, 2/n арифметика части определенного количества стола Ахмеса, эксплуатационные шаги должны быть переведены на современные арифметические заявления. Умножение Ahmes и методы подразделения были обратными друг другу с RMP 38, и AWT обеспечил яркие примеры арифметических отношений. RMP 36, для которого детали двух конверсионных методов рационального числа были детализированы, один для n/p, n/pq, 2/p и 2/pq и другого трудно, чтобы преобразовать n/p рациональные числа, которые были разобраны в разрешимый 2/p и (n-2)/p заявления. Египетское умножение содержало два аспекта, теоретическую сторону и практическую сторону. Египетское разделение рациональным числом было египетским умножением инверсией рационального числа. Ранние египетские ученые не рассмотрели теоретических аспектов RMP и других египетских текстов до 21-го века. Теоретические определения были скрыты в преобразовании рациональных чисел чешуйчатыми множителями, примененными в кратном правиле части. RMP 38 умножил hekat, заявил как 320 ro, 7/22, и возвратил 320 ro, умножив ответ на 22/7. Египетское подразделение было фактором и остатком базируемые, теоретические аспекты, которые ученые все более и более изучают с точки зрения кратных частей, 2/n таблицы и другие древние scribal заявления после 2005. См. также - Египетское умножение и разделение
- Ведическая математика Барати Кришны Тирты
Другие источники - Boyer, Карл Б. (1968) история А математики. Нью-Йорк: Джон Вайли.
- Браун, Кевин С. (1995) папирус Akhmin 1995---египетские части единицы.
- Брукхаймер, Максим, и И. Сэломон (1977) «Некоторые Комментарии к Анализу Р. Дж. Джиллингса 2/n Стола в Папирусе Rhind», Historia Mathematica 4: 445-52.
- Мишки, Эверт М. (1953) Фонтес matheseos: фургон hoofdpunten het prae-Griekse en Griekse wiskundig denken. Лейден:E. J. Камбала-ромб.
- -------(1957) «Platon et la table égyptienne 2/n», Янус 46: 253-63.
- Мишки, Эверт М (1981) «египетская арифметика», Янус 68: 33-52.
- -------(1981) «Приводимые и тривиальные разложения относительно египетской арифметики», Янус 68: 281-97.
- Бертон, Дэвид М. (2003) история математики: введение. Бостон Wm. К. Браун.
- Чэйс, Арнольд Баффум, и др. (1927) Математический Папирус Rhind. Оберлин: Математическая Ассоциация Америки.
- Кук, Роджер (1997) история математики. Краткий курс. Нью-Йорк, John Wiley & Sons.
- Couchoud, Сильвия. «Mathématiques égyptiennes». Recherches sur les connaissances mathématiques de l’Egypte pharaonique., Париж, Le Léopard d’Or, 1993.
- Daressy, Жорж. «Ахмим Вуд Тэблетс», Le Caire Imprimerie de l’Institut Francais d’Archeologie Orientale, 1901, 95–96.
- Кануны, Говард (1961) введение в историю математики. Нью-Йорк, Holt, Rinehard & Winston.
- Фаулер, Дэвид Х. (1999) математика Академии Платона: новая реконструкция. Оксфордский Унив. Нажать.
- Гардинер, Алан Х. (1957) египетская Грамматика, являющаяся Введением в Исследование Иероглифов. Издательство Оксфордского университета.
- Гарднер, Мило (2002) «Египетский математический кожаный рулон, заверенный краткий срок и длительный срок» в истории математических наук, Grattan-Guinness Ивора, Б.К. Ядава (редакторы), Нью-Дели, книга Agency:119-34 Индостана.
- --------«Математический рулон Египта» в энциклопедии истории науки, технологии и медицины в незападных культурах. Спрингер, ноябрь 2005.
- Джиллингс, Ричард Дж. (1962) «египетский Математический Кожаный Рулон», австралийский Журнал Науки 24: 339-44. Переизданный в его (1972) Математика во Время Фараонов. MIT Press. Переизданный Дуврскими Публикациями, 1982.
- --------(1974) «Лицевая сторона листа математического папируса Rhind: как древний египетский писец готовил его?» Архив для истории точных наук 12: 291-98.
- --------(1979) «Лицевая сторона листа RMP и EMLR», Historia Mathematica, Торонто 6 (1979), 442-447.
- --------(1981) «египетская Математическая Кожаная Ролевая линия 8. Как Писец Делал это?» Historia Mathematica: 456-57.
- Глэнвилл, S.R.K. «Математическая кожа сыплет британский музей” журнал египетской археологии 13, Лондон (1927): 232–8
- Гриффит, Фрэнсис Лльюелин. Папирусы Petrie. Культовые папирусы от Kahun и Gurob (Преимущественно среднего королевства), издания 1, 2. Бернард Куэрич, Лондон, 1898.
- Ганн, Бэттискомб Джордж. Обзор математического папируса Rhind Т. Э. Питом. Журнал египетской археологии 12 Лондона, (1926): 123–137.
- Hultsch, F, Die Elemente der Aegyptischen Theihungsrechmun 8, Ubersich uber умирают Lehre von den Zerlegangen, (1895):167-71.
- Imhausen, Аннетт. “Египетские Математические тексты и их Контексты”, Наука в Контексте 16, Кембридж (Великобритания), (2003): 367-389.
- Джозеф, Джордж Гевергезе. Вершина Павлиньих / Корней неевропейца Математики, Принстона, издательства Принстонского университета, 2 000
- Клее, Виктор, и фургон, Стэн. Старые и новые нерешенные проблемы в геометрии самолета и теории чисел, математической ассоциации Америки, 1991.
- Knorr, Уилбер Р. “Методы частей в древнем Египте и Греции”. Берлин Historia Mathematica 9, (1982): 133–171.
- Legon, Джон А.Р. “Математический фрагмент Kahun”. Обсуждения в египтологии, 24 Оксфорде, (1992).
- Люнеберг, H. (1993) «Zerlgung von Bruchen в Stammbruche» Леонарди Пизани Либер Аббачи Одер Lesevergnügen eines Mathematikers, Wissenschaftsverlag, Мангейм: 81=85.
- Малиновки, гей. и лоток Чарльза, математический папирус Rhind: древний египетский текст» Лондон, британская Museum Press, 1987.
- Roero, C. S. “египетская математика” Сопутствующая Энциклопедия Истории и Философия Математических Наук” я. Grattan-Guinness (редактор), Лондон, (1994): 30–45.
- Sarton, Джордж. Введение в историю науки, Vol I, Нью-Йорк, Williams & Son, 1 927
- Скотт, A. и зал, H.R., “отмечает лаборатория: египетский математический кожаный рулон семнадцатого века до н.э”, британский музей ежеквартально, Vol 2, Лондон, (1927): 56.
- Сильвестр, J. J. “На пункте в теории вульгарных частей”: американский журнал математики, 3 Балтимора (1880): 332–335, 388–389.
- Фогель, Курт. “Erweitert умирают Lederolle unserer Kenntniss ägyptischer мех Mathematik Archiv Geschichte der Mathematik, V 2, Юлиус Шустер, Берлин (1929): 386-407
- Ван-дер-Варден, Bartel Leendert. Научное Пробуждение, Нью-Йорк, 1 963
- Хана Вымазалова, деревянные таблетки от использования Cairo:The единицы зерна HK3T в древнем Египте, Archiv Orientalai, Чарльзе У Прага, 2002.
Внешние ссылки .org/encyclopedia/EgyptianMath4.html- http://weekly .ahram.org.eg/2007/844/heritage.htm
.org/encyclopedia/EgyptianMathematicalLeatherRoll2.html .org/encyclopedia/FirstLCMMethodRedAuxiliaryNumbers.html RMP 83 .org/encyclopedia/RationalNumbers.html- Российское крестьянское умножение
- Российский Крестьянский Алгоритм (файл PDF)
- Михаэль С. Шнайдер объясняет, как Древние египтяне (и китайский язык) и современные компьютеры умножают и делят
ru.knowledgr.com Математика в Древнем Египте — Туркмения ВиКиДанная статья — часть обзора История математики.Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому наши знания о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов — известно[1], что греческие математики учились у египтян[2]. Нам ничего не известно о развитии математических знаний в Египте как в более древние, так и в более поздние времена. После воцарения Птолемеев начинается чрезвычайно плодотворный синтез египетской и греческой культур. Источники Часть папируса Ахмеса.Задачи с 49 по 55. Основные сохранившиеся источники относятся к периоду Среднего царства, времени расцвета древнеегипетской культуры: - Папирус Ахмеса или папирус Ринда — наиболее объёмный манускрипт, содержащий 84 математические задачи. Написан около 1650 г. до н. э.
- Московский математический папирус (25 задач), около 1850 г. до н. э., 544 × 8 см.
- Так называемый «кожаный свиток» (англ.), 25 × 43 см.
- Папирусы из Лахуна (Кахуна) (англ.), содержащие ряд фрагментов на математические темы.
- Берлинский папирус (англ.), около 1300 года до н. э.
- Каирские деревянные таблички (таблички Ахмима).
- Папирус Рейснера (англ.), примерно XIX век до н. э.
От Нового царства до нас дошли несколько фрагментов вычислительного характера. Авторы всех этих текстов нам неизвестны. Дошедшие до нас экземпляры — это в основном копии, переписанные в период гиксосов. Носители научных знаний тогда именовались писцами и фактически были государственными или храмовыми чиновниками. Все задачи из папируса Ахмеса (записан ок. 1650 года до н. э.) имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и аликвотными дробями, пропорциональное деление, нахождение отношений, возведение в разные степени, определение среднего арифметического, арифметические прогрессии, решение уравнений первой и второй степени с одним неизвестным[3]. Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём индуктивных обобщений и гениальных догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет имела или, по крайней мере, начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни (целочисленные) и возводить в степень[4], решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры: при решении уравнений специальный иероглиф «куча» обозначал неизвестное. Нумерация (запись чисел) Иероглифическая запись числа 35736 Древнеегипетская нумерация, то есть запись чисел, была похожа на римскую: поначалу были отдельные значки для 1, 10, 100, … 10 000 000, сочетавшиеся аддитивно (складываясь). Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему. В иератическом письме уже есть отдельные обозначения для цифр 1-9 и сокращённые значки для разных десятков, сотен и тысяч. Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами. Например, чтобы написать число 30, можно было использовать обычные иероглифы: или то же самое написать цифрами (три символа десятки): Плита с гробницы принцессы Неферетиабет (2590—2565 до н. э., Гиза). Лувр Умножение египтяне производили с помощью сочетания удвоений и сложений. Деление заключалось в подборе делителя, то есть как действие, обратное умножению. Особые значки обозначали дроби вида 1n{\displaystyle {\frac {1}{n}}} и 23{\displaystyle {\frac {2}{3}}} . Однако общего понятия дроби mn{\displaystyle {\frac {m}{n}}} у них не было, и все неканонические дроби представлялись как сумма аликвотных дробей. Типовые разложения были сведены в громоздкие таблицы. Пример записи дробей из Папируса Ринда[5] 5 + 1⁄2 + 1⁄7 + 1⁄14 (= 5 5⁄7) Арифметика Знаки сложения и вычитания Чтобы показать знаки сложения или вычитания использовался иероглиф Если направление ног у этого иероглифа совпадало с направлением письма, тогда он означал «сложение», в других случаях он означал «вычитание».[6] Сложение Если при сложении получается число большее десяти, тогда десяток записывается повышающим иероглифом. Например: 2343 + 1671 + Собираем все однотипные иероглифы вместе и получаем: Преобразуем: Окончательный результат выглядит вот так: Умножение Основная статья: Умножение в Древнем Египте Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное переумножение на второй множитель Этот метод можно и сегодня встретить в очень отдаленных регионах. Разложение Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число. Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу значений: 1 x 2 = 22 x 2 = 44 x 2 = 88 x 2 = 1616 x 2 = 32 Пример разложения числа 25: - Кратный множитель для числа «25» — это 16.
- 25 — 16 = 9,
- Кратный множитель для числа «9» — это 8,
- 9 — 8 = 1,
- Кратный множитель для числа «1» — это 1,
- 1 — 1 = 0
Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1. Пример: умножим «13» на «238»: | ✔ | 1 х 238 | = 238 | | ✔ | 4 х 238 | = 952 | | ✔ | 8 х 238 | = 1904 | | | | 13 х 238 | = 3094 |
Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094. Уравнения Иероглифическая запись уравнения x(23+12+17+1)=37{\displaystyle x\left({\frac {2}{3}}+{\frac {1}{2}}+{\frac {1}{7}}+1\right)=37} Пример задачи из папируса Ахмеса: Найти число, если известно, что от прибавления к нему 2/3 его и вычитания из результата его трети получается 10.Геометрия Вычисление площадей В области геометрии египтяне знали точные формулы для площади прямоугольника, треугольника и трапеции. Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как S=a+c2⋅b+d2{\displaystyle S={\frac {a+c}{2}}\cdot {\frac {b+d}{2}}} ; эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику. Египтяне предполагали, что площадь круга S диаметром d равна площади квадрата, сторона которого составляет 8/9 диаметра: S=(d−d9)2=(89d)2.{\displaystyle S=\left(d-{\frac {d}{9}}\right)^{2}=\left({\frac {8}{9}}d\right)^{2}.} Это правило соответствует приближению π≈4⋅(89)2{\displaystyle \pi \approx 4\cdot \left({\frac {8}{9}}\right)^{2}} ≈ 3,1605 (погрешность менее 1 %)[7].. Некоторые исследователи[8] на основании 10-й задачи Московского математического папируса считали, что египтяне знали точную формулу для вычисления площади сферы, однако другие учёные с этим не согласны[9][10]. Вычисление объёмов Реконструкция водяных часов по чертежам из Оксиринха Египтяне могли высчитывать объёмы параллелепипеда, цилиндра, конуса и пирамид. Для вычисление объёма усечённой пирамиды египтяне пользовались следующим правилом: пусть мы имеем правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по следующей (правильной) формуле: V=(a2+ab+b2)⋅h4.{\displaystyle V=(a^{2}+ab+b^{2})\cdot {\frac {h}{3}}.} Древний свиток папируса, найденный в Оксиринхе, свидетельствует, что египтяне могли вычислять также объём усечённого конуса. Эти знания ими использовались для сооружения водяных часов. Так, например, известно, что при Аменхотепе III были построены водяные часы в Карнаке[источник не указан 1173 дня]. Египетский треугольник Египетским треугольником называется прямоугольный треугольник с соотношением сторон 3:4:5. Плутарх в первом веке об этом треугольнике в сочинении «Об Исиде и Осирисе» писал: «видимо, египтяне сравнивают природу Всеобщности с красивейшим из треугольников». Возможно, именно из-за этого этот треугольник получил название египетского[11]. Действительно, греческие учёные сообщали, что в Египте для построения прямого угла использовалась верёвка, разделённая на 12 частей. Египетский треугольник активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид. Историк Ван дер Варден попытался поставить этот факт под сомнение, однако более поздние исследования его подтвердили[12]. В любом случае, нет никаких свидетельств, что в Древнем Египте была известна теорема Пифагора в общем случае (в отличие от Древнего Вавилона)[13]. См. такжеПримечания - ↑ Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. Указ. соч., стр. 125: «Фалес путешествовал в Египет и привёз геометрию в Элладу» (из комментария Прокла к Евклиду).
- ↑ «Согласно большинству мнений, геометрия была впервые открыта в Египте, и возникла при измерении площадей» // Proclus Diadochus. In primum Euclidis Elementorum commentarii. — Leipzig, 1873. — С. 64.
- ↑ История математики, том I, 1970, с. 21—33..
- ↑ История математики, том I, 1970, с. 24..
- ↑ Gardiner Alan H. Egyptian grammar: being an introduction to the study of hieroglyphs 3rd ed., rev. London: 1957, p. 197.
- ↑ Cajori, Florian. A History of Mathematical Notations. — Dover Publications, 1993. — P. pp. 229–230. — ISBN 0486677664.
- ↑ История математики, том I, 1970, с. 30—32..
- ↑ W. W. Struve. Mathematischer Papyrus des Museum in Moskau. — Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung A. — Berlin: Springer, 1930. — С. 157.
- ↑ История математики, том I, 1970, с. 31—32..
- ↑ Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции, стр. 44-45
- ↑ Прасолов В. В. Глава 1. Древний Египет и Вавилон // История математики. — (не публиковалась), 2013. — С. 5.
- ↑ Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Физматлит, 1959, С. 13, подстрочное примечание
- ↑ История математики, том I, 1970, с. 31..
Литература - Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — 456 с.
- Веселовский И. Н. Египетская наука и Греция. Труды ИИЕ, 2, 1948, с. 426—498.
- Выгодский М. Я. Арифметика и алгебра в древнем мире. — М.: Наука, 1967.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд. второе. — М.: Просвещение, 1965. — 416 с.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Нейгебауер О. Лекции по истории античных математических наук. — Москва-Ленинград, 1937.
- Раик А. Е. Две лекции о египетской и вавилонской математике // Историко-математические исследования. — М.: Физматгиз, 1959. — № 12. — С. 271-320.
- Раик А. Е. Очерки по истории математики в древности. Саранск: Мордовское гос. изд-во, 1977.
- Gillings R. J. Mathematics in the time of the pharaohs. Cambridge: MIT Press, 1972.
- Rossi C. Architecture and mathematics in Ancient Egypt. Cambridge (UK): Cambridge UP, 2004.
- Vogel K. Vorgriechische Mathematik I, Vorgeschichte und Ägypten. Hannover: Schrödel, 1958.
Ссылкиtm.ru.net definition of Математика_в_Древнем_Египте and synonyms of Математика_в_Древнем_Египте (Russian)Материал из Википедии — свободной энциклопедииДанная статья — часть обзора История математики. О математике в Древнем Египте Часть папируса Ахмеса.Задачи с 49 по 55. Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. К сожалению, египтяне писали на папирусе, который сохраняется плохо, и поэтому наши знания о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов — общеизвестно, что греческие математики учились у египтян. Основные сохранившиеся источники: папирус Ахмеса или папирус Ринда (84 математические задачи) и московский математический папирус (25 задач), оба из Среднего царства, времени расцвета древнеегипетской культуры. Авторы текста нам неизвестны. Дошедшие до нас экземпляры — это копии, переписанные в период гиксосов. Носители научных знаний тогда именовались писцами и фактически были государственными или храмовыми чиновниками. Все задачи из папируса Ахмеса (записан ок. 1650 года до н. э.) имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и аликвотными дробями, пропорциональное деление, нахождение отношений, возведение в разные степени, определение среднего арифметического, арифметические прогрессии, решение уравнений первой и второй степени с одним неизвестным[1]. Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём индуктивных обобщений и гениальных догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет имела или по крайней мере начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни и возводить в степень, решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры: при решении уравнений специальный иероглиф «куча» обозначал неизвестное. Нам ничего не известно о развитии математических знаний в Египте как в более древние, так и в более поздние времена. После воцарения Птолемеев начинается чрезвычайно плодотворный синтез египетской и греческой культур. Нумерация Иероглифическая запись числа 35736 Древнеегипетская нумерация, то есть запись чисел, была похожа на римскую: поначалу были отдельные значки для 1, 10, 100, … 10 000 000, сочетавшиеся аддитивно (складываясь). Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему. В иератическом письме уже есть отдельные обозначения для цифр 1-9 и сокращённые значки для разных десятков, сотен и тысяч. Умножение египтяне производили с помощью сочетания удвоений и сложений. Деление заключалось в подборе делителя, то есть как действие, обратное умножению. Особые значки обозначали дроби вида  и и  . Однако общего понятия дроби . Однако общего понятия дроби  у них не было, и все неканонические дроби представлялись как сумма аликвотных дробей. Типовые разложения были сведены в громоздкие таблицы. у них не было, и все неканонические дроби представлялись как сумма аликвотных дробей. Типовые разложения были сведены в громоздкие таблицы. Файл:Egypt equation.gif Пример иероглифической записи уравнения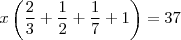 Пример записи дробей из Папируса Ринда[2] <hiero>Z2:Z1*Z1 Aa16 r:Z1*Z1*Z1*Z1:Z2 r:10 Z1-Z1-Z1-Z1</hiero>5 + 1⁄2 + 1⁄7 + 1⁄14 (= 5 5⁄7) Запись чиселЧисла в Древнем Египте записывали двумя способами: словами и цифрами. Например, чтобы написать число 30, можно было использовать обычные иероглифы:<hiero>Aa15:D36-D58</hiero>или то же самое написать цифрами (три символа десятки):<hiero>V20-V20-V20</hiero> Обоими способами можно было записывать любые числа. Знаки сложения и вычитанияЧтобы показать знаки сложения или вычитания использовался иероглиф | <hiero>D54</hiero> или <hiero>D55</hiero> |
Если направление ног у этого иероглифа совпадало с направлением письма, тогда он означал «сложение», в других случаях он означал «вычитание».[3] СложениеЕсли при сложении получается число большее десяти, тогда десяток записывается повышающим иероглифом. Например: 2343 + 1671 <hiero>M12-M12-V1*V1:V1-V20*V20:V20*V20-Z1:Z1:Z1</hiero> + <hiero>M12-V1*V1*V1:V1*V1*V1-V20*V20*V20*V20:V20*V20*V20*Z1</hiero> Собираем все однотипные иероглифы вместе и получаем: <hiero>M12-M12-M12-V1*V1*V1*V1*V1:V1*V1*V1*V1*V20-V20*V20*V20*V20*V20:V20*V20*V20*V20*V20-Z1*Z1:Z1*Z1</hiero> Преобразим: <hiero>M12-M12-M12-V1*V1*V1*V1*V1:V1*V1*V1*V1*V1-V20-Z1*Z1:Z1*Z1</hiero> Окончательный результат выглядит вот так: <hiero>M12*M12:M12*M12-V20-Z1*Z1:Z1*Z1</hiero> УмножениеОсновная статья: Умножение в Древнем Египте Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать числа им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное переумножение на второй множитель (см. пример). Этот метод можно и сегодня встретить в очень отдаленных регионах. РазложениеЕгиптяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число. Чтобы правильно подобрать кратное число нужно было знать следующую таблицу значений: 1 x 2 = 22 x 2 = 44 x 2 = 88 x 2 = 1616 x 2 = 32 Пример разложения числа 25: - Кратный множитель для числа «25» - это 16.
- 25 – 16 = 9,
- Кратный множитель для числа «9» - это 8,
- 9 – 8 = 1,
- Кратный множитель для числа «1» - это 1,
- 1 – 1 = 0
Таким образом «25» - это сумма трех слагаемых: 16, 8 и 1. ПримерУмножим «13» на «238»: | ✔ | 1 х 238 | = 238 | | ✔ | 4 х 238 | = 952 | | ✔ | 8 х 238 | = 1904 | | | 13 х 238 | = 3094 |
Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094. Арифметика и геометрияВ области геометрии египтяне знали точные формулы для площади прямоугольника, треугольника, трапеции и сферы, могли высчитывать объемы параллелепипеда, цилиндра и пирамид. Формулы египетской геометрииПлощадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как 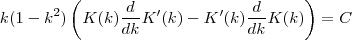 ; эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику. ; эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику. Египтяне предполагали, что 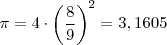 (погрешность менее 1 %)[4]. (погрешность менее 1 %)[4]. Формула площади круга с диаметром d имела вид: 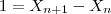 Ещё одна ошибка содержится в Акмимском папирусе[5]:автор считает, что если радиус круга A есть среднее арифметическое радиусов двух других кругов B и C, то и площадь круга A есть среднее арифметическое площадей кругов B и C. Вычисление объема усеченной пирамиды: пусть мы имеем правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по оригинальной, но точной формуле: 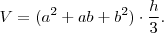 Египетский треугольник Египетский треугольник Египетским треугольником называется прямоугольный треугольник с соотношением сторон 3:4:5. Объем усеченного конуса Реконструкция водяных часов по чертежам из ОксиринхаДревний свиток папируса, найденный в Оксиринхе, свидетельствует, что египтяне могли вычислять объем усеченного конуса. Эти знания ими использовались для сооружения водяных часов. Так, например, известно, что при Аменхотепе III были построены водяные часы в Карнаке. См. также Примечания- ↑ История математики под редакцией А. П. Юшкевича в трёх томах, М., Наука, 1970, том 1, стр.21-33.
- ↑ Gardiner Alan H. Egyptian grammar: being an introduction to the study of hieroglyphs 3rd ed., rev. London: 1957, p. 197.
- ↑ Florian Cajori A History of Mathematical Notations. — Dover Publications, 1993. — P. pp. 229–230. — ISBN 0486677664
- ↑ История математики под редакцией А. П. Юшкевича в трёх томах, М., Наука, 1970, том 1, стр.30-32.
- ↑ Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — С. 279.
Литература- Бобынин В. В. Математика древних египтян (по папирусу Ринда). М.: 1882.
- Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Гос. изд. физ-мат. лит., 1959.
- Веселовский И. Н. Египетская наука и Греция. Труды ИИЕ, 2, 1948, с. 426–498.
- Выгодский М. Я. Арифметика и алгебра в Древнем мире. Изд. 2-е. М.: Наука, 1967.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд. второе. — М.: Просвещение, 1965. — 416 с.
- История математики с древнейших времен до начала Нового времени / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Нейгебауер О. Лекции по истории античных математических наук. — Москва-Ленинград: 1937.
- Раик А. Е. Очерки по истории математики в древности. Саранск: Мордовское гос. изд-во, 1977.
- Gillings R. J. Mathematics in the time of the pharaohs. Cambridge: MIT Press, 1972.
- Rossi C. Architecture and mathematics in Ancient Egypt. Cambridge (UK): Cambridge UP, 2004.
- Vogel K. Vorgriechische Mathematik I, Vorgeschichte und Ägypten. Hannover: Schrödel, 1958.
dictionary.sensagent.com Технологическая карта урока по математике на тему:"Как умножали в Древнем Египте". Технологическая карта по математике во 2 классе УМК «Планета знаний» Студент-практикант: Островерхова Яна Владимировна. Предметная область: математика. Класс: 2В. Тема: «Как умножали в Древнем Египте». Тип: урок получения новых знаний. Цель: познакомить обучающихся с египетским способом умножения. Задачи: совершенствовать вычислительные навыки, умение решать задачи, примеры; развивать внимание, логическое мышление, математическую речь.
Формируемые УУД Личностные: выражать положительное отношение к процессу познания: проявлять внимание, удивление, желание больше узнать; оценивать собственную учебную деятельность: свои достижения, самостоятельность, инициативу, ответственность, причины неудач; проявлять интерес к учебному материалу; способность к самооценке на основе критерия успешности учебной деятельности.
Регулятивные: уметь определять и формулировать тему и цель на уроке с помощью учителя; уметь планировать свое действие в соответствии с поставленной задачей; уметь высказывать свое предположение на основе работы с материалом учебника; оценивать правильность выполнения действия на уроке; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; выполнять под руководством учителя учебные действия в практической и мыслительной форме; фиксировать в диалоге с учителем в конце урока удовлетворённость/неудовлетворённость своей работой на уроке.
Познавательные: структурирование знаний; осознанное и произвольное построение речевого высказывания в устной форме; делать выводы в результате совместной работы класса и учителя; находить ответы на вопросы, используя различные средства обучения. ориентироваться в информационном материале учебника; осуществлять поиск необходимой информации (по необходимости совместно с учителем).
Коммуникативные: планирование учебного сотрудничества со сверстниками; уметь оформлять свои мысли в устной форме; слушать и понимать речь других; включаться в диалог с учителем; осуществлять взаимоконтроль и взаимную помощь; уважать другую точку зрения.
Предметные: Личностные: Метапредметные: уметь определять и формулировать цель урока; проговаривать последовательность действий на уроке; работать по план; оценивать правильность выполнения действия; планировать свои действия в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.
Планируемый результат: познакомить учеников с системой умножения в Древнем Египте. Этапы урока Деятельность учителя Деятельность учащихся Обучающие и развивающие задания каждого этапа УУД I. Орг. момент II. Постановка цели урока. III. Актуализация целей изучаемой темы. Устный счет. - Здравствуйте ребята! Ну-ка проверь, дружок, Ты готов начать урок? Все ли правильно сидят? Все ль внимательно глядят? Всё ль на месте? Всё ль в порядке? Ручка, книжка и тетрадки? Соберись и улыбкой поделись! - Ребят, давайте улыбнемся друг другу, подарим свою улыбку окружающим. - Сегодня, у нас с вами будет не простой урок математики, мы отправимся с вами в путешествие в Древний Египет и побудем настоящими египтянами, а я буду вашей предводительницей и наша сегодняшняя задача найти сокровища Фараона Тутанхамона. Каждое задание, выполненное правильно откроет для нас какую-то достопримечательность Древнего Египта. -Вы знаете, кто такой Фараон Тутанхамон? -А каких знаменитых людей Древнего Египта вы знаете? - Как вы думаете, что станет темой нашего путешествия? - Какую цель можно поставить перед собой? - Ну, что ж мы готовы к путешествию. И так ребята, мы с вами в Древнем Египте. - И первое, что мы сделаем, это запишем число, классная работа в тетрадь, но это не простая тетрадь, это папирус, но при письме мы должны соблюдать все правила. -А вы знаете, что такое папирус? (Диктовка). - Давайте посмотрим 1 наше задание: перед нами пирамида Хеопса, нужно перемножить все эти цифры на 2. Я показываю на ученика, вы сразу говорите мне ответ. Приветствуют учителя. Проверяют рабочие места. Улыбаются друг другу и гостям. Слушают учителя. -Предводитель, царь. -Царица Клеопатра, царица Нефертити (самая красивая царица Египта), Фараон Рамзес. -Древний Египет, умножение в Древнем Египте. - Найти сокровища Фараона и разгадать все задачи, которые нам будут встречаться на пути. Слушают Записывают Это бумага, на котором писали в Древнем Египте. Слушают. Проговаривают ответы. 28 я н в а р я К л а с с н а я р а б о т а 2*2=4 3*2=6 4*2=8 5*2=10 6*2=12 7*2=14 личностные (мотивация к учебной деятельности) метапредметные (организация взаимопомощи) регулятивные (прогнозирование) личностные регулятивные (предвосхищение результата и уровня усвоения знаний) IV. Применение теоретических положений в условиях выполнения заданий. V. Физ. минутка. VI. Самостоятельное использование сформированных умений и навыков. VII. Итог урока. Рефлексия. - И так, задание выполнено, теперь Фараон, просит нас открыть учебник на с.24 и давайте прочитаем «Как умножали в Древнем Египте», чтобы стать настоящими египтянами. - Давайте решим эту задачу. Египтяне не умели просто взять и умножить, как мы уже привыкли. Они клали товар с одной стороны, а деньги с другой. Стоимость 1 рыбы 3 монеты. Вы хотите купить 16 рыб (показывать наглядно). Смотрите, я половина рыб откладываю, вы мне за них платите не 3 монеты, а в 2 раза больше, сколько это будет. Затем из 8 оставшихся рыб, откладываем еще половину, сколько у нас остается. Вы заплатили сколько монет? А теперь вы должны заплатить еще в 2 раза больше сколько это будет? Теперь из оставшихся 4 рыб, я откладываю еще половину, сколько остается? Тогда вы заплатили 12 монет, а сейчас еще в 2раза больше, сколько это будет? Из 2 умы убираем еще половину, т.е. остается 1, вы заплатите еще в 2 раза больше, сколько вы перед этим заплатили? А сколько сейчас заплатим? Ну вот, задача решена. Интерактивная физ. минутка. Следующее наше задание на с.25 №1, вы выполните его в парах. Затем мы его проверим. Проверка. Записывают в тетрадь. - Как изменяются множители? - Какой это способ умножения? Вызывает ученика, который проводит физ. минутку. - Следующее задание 2, вы выполните каждый самостоятельно, затем мы проверим, но сначала прочитаем правило. И так, давайте проверим. - И так, мы и добрались до сокровища Фараона. - Что нового, вы сегодня узнали из нашего путешествия? - Чему научились? - Теперь, на столах у вас лежат смайлы: РАДОСТЬ и ГРУСТЬ, давайте оценим наше путешествие, понравилось нам или нет, поднимите смайлы вверх. - Спасибо за урок! Слушают. Читают. 3*2=6 4 6 6*2=12 2 12*2=24 24 24*2=48 Первый множитель уменьшается на 2, а второй увеличивается на 2. Древне - египетский Один показывает и проговаривает, а все другие повторяют. Слушают. Выполняют задание. 4*13=52 2*26=52 1*52=52 8*12=96 4*24=96 2*48=96 1*96=96 16*6=96 8*12=96 4*24=96 2*48=96 1*96=96 Слушают Отвечают на вопросы. Поднимают смайлы 8*2=16 9*2=18 Учебник, с.24 Учебник, с.25 №1. 4*5=20 8*3=24 2*10=20 4*6=24 1*20=20 2*12=24 Учебник, с.25 №2. 4*13=52 8*12=96 16*6=96 Смайлы: Радость – путешествие понравилось; Грусть – путешествие не понравилось. предметные познавательные познавательные, коммуникативные коммуникативные, предметны познавательные личностные познавательные, коммуникативные, регулятивные регулятивные, личностные Подпись методиста (Афанасьева Надежда Петровна): Подпись учителя (Балюк Светлана Вячеславовна): infourok.ru
|
