V Международный конкурс научно-исследовательских и творческих работ учащихся Старт в науке. Древние способы умножения
Необычные способы умножения МОУ «Куровская средняя общеобразовательная школа №6» РЕФЕРАТ ПО МАТЕМАТИКЕ НА ТЕМУ: «НЕОБЫЧНЫЕ СПОСОБЫ УМНОЖЕНИЯ». Выполнил ученик 6 «б» класса Крестников Василий. Руководитель: Смирнова Татьяна Владимировна. 2011г. Оглавление. Вступление…………………………………………………………………………2 Основная часть. Необычные способы умножения…………………………3 2.1. Немного истории………………………………………………………………..3 2.2. Умножение на пальцах…………………………………………………………4 2.3. Умножение на 9…………………………………………………………………5 2.4. Индийский способ умножения……………………………………………….6 2.5. Умножение способом «Маленький замок»…………………………………7 2.6. Умножение способом «Ревность»……………………………………………8 2.7. Крестьянский способ умножения……………………………………………..9 2.8 Новый способ…………………………………………………………………..10 Заключение………………………………………………………………………11 Список литературы…………………………………………………………….12 1 I. Вступление. Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе. Однажды мне случайно попалась книга С. Н. Олехника, Ю. В. Нестеренко и М. К. Потапова «Старинные занимательные задачи». Листая эту книгу, мое внимание привлекла страничка под названием «Умножение на пальцах». Оказалось, что можно умножать не только так как предлагают нам в учебниках математики. Мне стало интересно, а есть ли еще какие-нибудь способы вычислений. Ведь способность быстро производить вычисления вызывает откровенное удивление. Постоянное применение современной вычислительной техники приводит к тому, что учащиеся затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или счетной машины. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического цикла. Цель работы: Показать необычные способы умножения. Задачи: Найти как можно больше необычных способов вычислений. Научиться их применять. Выбрать для себя самые интересные или более легкие, чем те которые предлагаются в школе, и использовать их при счете. 2 II. Основная часть. Необычные способы умножения. 2.1. Немного истории. Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера. Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия. В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». И все эти приемы умножения — «шахматный или органчиком», «загибанием», «крестиком», «решеткой», «задом наперед», «алмазом» и прочие соперничали друг с другом и усваивались с большим трудом. Давайте рассмотрим наиболее интересные и простые способы умножения. 3 2.2. Умножение на пальцах. Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались. Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.  4 2.3. Умножение на 9. Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).  Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».  Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто. 7 клеток 2 клетки. 5 2.4. Индийский способ умножения. Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам. Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6: 537 6 (5 ∙ 6 =30) 30 537 6 (300 + 3 ∙ 6 = 318) 318 537 6 (3180 +7 ∙ 6 = 3222) 3222 6 2.5. Умножение способом «МАЛЕНЬКИЙ ЗАМОК». Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет. За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение». Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину. Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.  7 2.6. Умножение чисел методом «ревность».  Второй способ носит романтическое название «ревность», или «решётчатое умножение». Второй способ носит романтическое название «ревность», или «решётчатое умножение». Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь». Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29. В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063. 3 4 7 2 9 10 0 6 3 8 2.7. Крестьянский способ умножения. Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением 37……….32 74……….16 148……….8 296……….4 592……….2 1184……….1 Произведение всех пар соответственных чисел одинаковое, поэтому 37 ∙ 32 = 1184 ∙ 1 = 1184 В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом: 24 ∙ 17 24 ∙ 16 = = 48 ∙ 8 = = 96 ∙ 4 = = 192 ∙ 2 = =384 ∙ 1 = 384 24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408 9 2.8. Новый способ умножения. Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе. Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35 Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений. В итоге получаем: 078235. Число 78235 и есть результат умножения. Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.  10 III. Заключение. Научившись считать всеми представленными способами, я пришел к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны. Из всех найденных мною необычных способов счета более интересным показался способ «решетчатого умножения или ревность». Я показал его своим одноклассникам, и он им тоже очень понравился. Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел). Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами. Я думаю, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы. 11 Литература. Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954. – 140 с. Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/ Олехник С. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с. Перельман Я.И. Занимательная арифметика. М.Русанова,1994—205с. Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004. Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с. 12 sundekor.ru Виды умножения | Проекты 
проблема : разобраться видах умножения Цель:ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.Задачи:1. Найти и разобрать различные способы умножения.2. Научиться демонстрировать некоторые способы умножения.3. Рассказать о новых способах умножения и научить ими пользоваться учащихся.4. Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.5. Эксперимент «какой способ быстрей»Гипотеза:Надо ли знать таблицу умножения?Актуальность:В последнее время ученики доверяют гаджетам больше чем себе. И по этому считают только на калькуляторах. Мы хотели показать что есть разные способы умножение, что бы ученикам было легче считать,и интересно учить.ВВЕДЕНИЕВы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.В разное время разные народы владели разными способами умножения натуральных чисел.Почему же сейчас все народы применяют один способ умножения «столбиком»?Почему люди отказались от старых способов умножения в пользу современного?Имеют ли забытые способы умножения право на существование в наше время?Что бы ответить на эти вопросы я проделал следующую работу:1. С помощью сети Интернета нашел информацию о некоторых способах умножения, которые использовались раньше.;2. Изучил литературу, предложенную учителем;3. Решил пару примеров всеми изученными способами, что бы узнать их недостатки;4) Выявил среди них наиболее эффективные;5. Провел эксперимент;6. Сделал выводы.1. Найти и разобрать различные способы умножения.Умножение на пальцах. Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались. Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5. Способы умножения чисел в разных странах 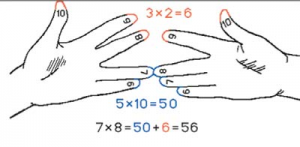
Умножение на 9. Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).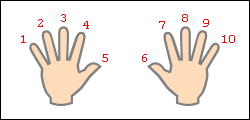 Кто придумал умножение на пальцах Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».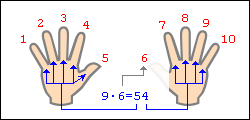 Умножение необычным способом Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто. 7 клеток 2 клетки. 5 Индийский способ умножения.Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам. Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6: 537 6 (5 ∙ 6 =30) 30 537 6 (300 + 3 ∙ 6 = 318) 318 537 6 (3180 +7 ∙ 6 = 3222) 3222 6 Умножение способом «МАЛЕНЬКИЙ ЗАМОК». Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет. За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение». Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину. Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются. Способы умножения чисел в разных странах 7 Умножение чисел методом «ревность». 
«Методы умножения Второй способ носит романтическое название ревность», или «решётчатое умножение». Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь». Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29. В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063. 3 4 7 6 8 1 4 2 7 3 6 6 3 2 9 10 0 6 3 8 Крестьянский способ умножения. Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением 37……….32 74……….16 148……….8 296……….4 592……….2 1184……….1 Произведение всех пар соответственных чисел одинаковое, поэтому 37 ∙ 32 = 1184 ∙ 1 = 1184 В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом: 24 ∙ 17 24 ∙ 16 = = 48 ∙ 8 = = 96 ∙ 4 = = 192 ∙ 2 = =384 ∙ 1 = 384 24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408Новый способ умножения. Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе. Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35 Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений. В итоге получаем: 078235. Число 78235 и есть результат умножения. Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.  Умножение графическим методом (линейным, китайским) Умножение графическим методом (линейным, китайским)
Перемножим два двузначных числа: 15*23 Шаг 1. первое число 15: Рисуем первую цифру – одной линией. Рисуем вторую цифру – пятью линиями. Шаг 2. второе число 23: Рисуем первую цифру – двумя линиями. Рисуем вторую цифру – тремя линиями. Шаг 3.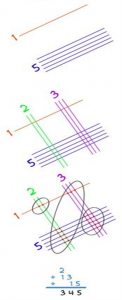 Подсчитываем количество точек в группах. Подсчитываем количество точек в группах. Шаг 4. Результат – 345 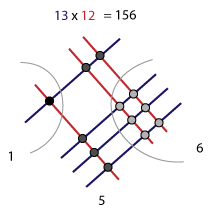 Проведем эксперимент Проведем эксперимент
С помощью секундомера установим сколько времени затрачивается на решение примера, каждым рассмотренным способом. Сравним результаты пример Крестьянский Метод решетки(ревность) Результат опрос комикс презезентация хронологическая лента Тизер Заключение. Работая над этой темой, я узнал, что существует порядка 30 различных, забавных и интересных способов умножения. Некоторыми в различных странах пользуются до сих пор. Я выбрал для себя некоторые интересные способы. Но не все способы удобны в использовании, особенно при умножении многозначных чисел. Способы умножения iteach.vspu.ru Способы умножения Способы умножения Мусина Алина Александровна 11МКОУ Ордынского района Новосибирской области – Ордынская средняя общеобразовательная школа № 1 имени Героя Советского Союза А.Д.Гаранина Протасова Наталия Владимировна 11МКОУ Ордынского района Новосибирской области – Ордынская средняя общеобразовательная школа № 1 имени Героя Советского Союза А.Д.Гаранина Текст работы размещён без изображений и формул.Полная версия работы доступна во вкладке "Файлы работы" в формате PDF Введение Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе. А можно ли умножать не только так, как предлагают нам в учебниках математики? Мне стало интересно, а есть ли еще какие-нибудь способы вычислений. Ведь способность быстро производить вычисления вызывает откровенное удивление и восторг окружающих. В нашем современном обществе, когда у каждого есть телефон с калькулятором, мы всё чаще и чаще используем его, забывая, как можно без всякой техники легко и быстро выполнить умножение больших чисел. Постоянное применение современной вычислительной техники приводит к тому, что ученики затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или калькулятора. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического направления.[1] Актуальность исследования: Несмотря на то, что наша жизнь в последние годы стала значительно легче благодаря обилию доступных электронных счетных устройств, навык быстрого и удобного умножения не потерял своей актуальности для человека. Гипотеза исследования: Существуют другие способы умножения, которые легче и быстрее традиционного умножения столбиком. Объект исследования: арифметическое действие «умножение». Предмет исследования: различные нестандартные способы умножения. Методы исследования: Поиск разных способов умножения Сравнение найденных способов и выявление их преимуществ и недостатков Обобщение изученной информации Цель исследования: Выявить и изучить новые способы умножения Задачи: Изучить литературу по данной теме; Отобрать самые интересные и простые способы; Научиться применять найденные способы умножения; Проверить экспериментальным путём степень сложности каждого способа; Проанализировать и выявить плюсы и минусы отобранных способов; Провести мастер – классы по знакомству с нетрадиционными способами; Провести анкетирование; Составить буклеты – памятки самых простых и интересных способов; Собрать электронную копилку видеоуроков по разным способам. Глава 1. Из истории умножения Умножение - это особый случай сложения нескольких одинаковых чисел. В далекие времена люди учились умножать уже при счете предметов. Так, считая по порядку числа 17, 18, 19, 20, они должны были представлять 20 не только как 10+10, но и как два десятка, 30 - как три десятка,- и так далее. Умножать люди начали значительно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложения или последовательного удвоения. В Вавилоне при умножении чисел пользовались специальными таблицами умножения - «предками» современных. В Древней Индии применяли способ умножения чисел, тоже довольно близкий к современному. Индийцы производили умножение чисел, начиная с высших разрядов. При этом они стирали те цифры, которые при последующих действиях надо было заменять, так как к ним прибавляли число, ныне запоминаемое нами при умножении. Таким образом, математики Индии сразу записывали произведение, выполняя промежуточные вычисления на песке или в уме. Индийский прием умножения перешел к арабам. Но арабы не стирали цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой. В Европе продолжительное время произведение называли сумма умножения. Название «множитель» упоминается в работах VI века, а «множимое» - в XIII веке. В XVII веке некоторые из математиков стали обозначать умножение косым крестиком, а иные употребляли для этого точку. Только в конце XVIII века большинство математиков стали употреблять в качестве знака умножения точку, но допускали и употребление косого креста. Знаки умножения и знак равенства стали общепризнанными благодаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница (1646 -1716).[2] В современной школе умение быстро умножать многозначные числа, которое школьники получают к концу начальной школы, постепенно без постоянных систематических тренировок в среднем звене, теряет своё прямое назначение. Многие школьники не скрывают, что пользуются всё чаще при вычислениях калькулятором. И лишь по требованию учителя, показать развёрнутый полный ответ, прописывают решения примеров столбиками. Эксперты ЕГЭ ежегодно приходят к выводу, что навык простого умножения в столбик к 11 классу сохраняется не у всех. Но так как это основные базовые знания выпускника, поэтому в заданиях ОГЭ и ЕГЭ всегда присутствуют задания на умножение многозначных чисел. А может быть существуют другие, более лёгкие способы счёта, о которых известно мало? Возможно, не во всех странах используют столбик? Эти и другие похожие вопросы и легли в основу моего исследования по поиску и изучению необычных способов умножения. Для того, чтобы понять, знают ли окружающие нестандартные способы умножения на практике, я провела небольшой опрос по данной теме. В опросе участвовало три группы: младшие школьники, подростки и взрослые. Участников опроса просили ответить на три вопроса: - Как вы обычно умножаете многозначные числа, если у вас нет калькулятора? - Знаете ли вы нестандартные способы умножения? - Если да, то, какие? Эта анкета была проведена для того, чтобы выявить знание других способов. По результатам опроса можно сделать вывод, что большинство опрошенных не знают другие нестандартные способы умножения. Несколько малышей знакомы со способом счёта на пальцах, четверо подростков пояснили, как считать японским способом, а четверо – древнерусским. Опрос взрослых показал, что только семь человек знают другие нестандартные способы: японский и умножение на пальцах. (Приложение 1) Результаты опроса ещё больше убедили меня заняться более глубоким исследованием этого вопроса. И вот что я нашла. Коротко о самых интересных способах. Глава 2. Японский или китайский способ умножения Использование приема: Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок: Этот рисунок состоит из 10 линий. Эти линии обозначают число 24 (2 линии, отступ, 4 линии) и число 13 (1 линия, отступ, 3 линии). Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом: (пересечения на рисунке указаны точками) Количество пересечений: Верхний левый край: 2 Нижний левый край: 6 Верхний правый: 4 Нижний правый: 12 1) Пересечения в верхнем левом крае (2) – первое число ответа 2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа 3) Пересечения в нижнем правом крае (12) – третье число ответа. Получается: 2; 10; 12. Так как два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему. 3(2+1)1(0+1)2 Ответ: 312[3] Глава 3. Итальянский способ умножения «Сеткой» В Италии, а также во многих странах Востока, этот способ приобрел большую известность. Использование приема: Например, умножим 6827 на 345. 1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте. 2. Умножаем число каждого ряда последовательно на числа каждой колонки. 6∙3 = 18. Записываем 1 и 8 8∙3 = 24. Записываем 2 и 4 3.Если при умножении получается однозначное число, записываем вверху 0, а внизу это число. ( Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6) Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево снизу. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали. Ответ: 2355315. [3] Глава 4. Индийский способ умножения Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких-нибудь разрядов, определяется нулями, приписываемыми к цифрам. Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:[4] Глава 5. Древнерусский способ Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались. Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2∙3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.[5] Также известен и способ умножения на пальцах на 9. (Приложение 2) Глава 6. Русский крестьянский способ В России среди крестьян был распространен способ, который не требовал знания всей таблицы умножения. Здесь необходимо лишь умение умножать и делить числа на 2. Напишем одно число слева, а другое справа на одной строке. Левое число будем делить на 2, а правое – умножать на 2 и результаты записывать в столбик. Если при делении возник остаток, то его отбрасывают. Умножение и деление на 2 продолжают до тех пор, пока слева не останется 1. Затем вычеркиваем те строчки из столбика, в которых слева стоят четные числа. Теперь сложим оставшиеся числа в правом столбце. [5] Глава 7.«Умножение крестиком» из Древней Греции Древние греки и индусы в старину называли прием перекрестного умножения «способом молнии» или «умножение крестиком». Пример: 63 х 92 = 5796 6 3 X 9 2 Последовательно производим следующие действия: 1. 3 х 2 = 6 – это последняя цифра результата. 2. 6 х 2 = 12; ,3 х 9 = 27; 12 + 27 = 39. 9 – предпоследняя цифра в ответе, 3 запоминаем. 3. 6 х 9 = 54, 54 + 3 = 57 – это первые цифры в ответе. Ответ: 5796. Этим способом удобно пользоваться и в настоящее время. [5] Глава 8. Египетское умножение В мире существуют разные способы умножения, порой непривычные для нас, совсем непохожие на наши правила умножения. К примеру, в Древнем Египте не было таблиц умножения. Но они умножали разложением чисел в двоичный ряд - так называемый «компьютерный» способ. Например, нужно умножить 26 на 47. 1. Записываем 26 и 47. 2. Теперь левое число делим на 2, а правое умножаем на 2. 3. Так продолжается, пока в левой колонке не появится 1. ( Нечетные числа при делении на 2 округляем в сторону меньшего.) Если число в левой колонке нечетное, то мы его отмечаем «плюсиком» Теперь складываем отмеченные числа: 94 + 376 + 752 = 1222 [6] Глава 9. Умножение чисел с помощью опорного числа Автором способа является американец Билл Хэндли. Данный способ умножения очень интересный. Он позволяет не запоминать таблицу умножения целиком, так как она изучается в школьном курсе математики. Первое правило математики Билла Хэндли выглядит так: «Чем проще метод, используемый вами для решения задачи, тем быстрее вы ее решите и тем меньше вероятность того, что вы допустите ошибку» (3, 12). Билл Хэндли предлагает при умножении чисел использовать опорное число. В качестве опорных чисел он выбирает числа, на которые легко умножать. Опорное число полезно при перемножении чисел, находящихся близко и при возведении в квадрат. При умножении чисел до 100, в качестве опорных, удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100. Вы, наверное, зададите вопрос, почему именно эти числа, а не другие. Ответ очень прост, потому что при умножении на 10 и 100 всего лишь следует приписать справа от числа количество нулей соответствующих числам 10 и 100. Когда берем 20 в качестве опорного числа, то 20 это 10 умноженное на 2, что легко посчитать, а 50 это половина 100, поэтому чтобы умножить на 50, можно умножить число, сначала на 100, а затем разделить результат на 2. Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая: оба множителя меньше опорного; оба множителя больше опорного; один из множителей больше, а другой меньше опорного. [7] Использование этого метода требует пошаговой работы с алгоритмом. (Приложение 3) Глава 10. Умножение способом «Маленький замок» из Средних веков Умножение чисел сейчас изучают в начальной школе. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет. За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок». Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину. Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.[5] Глава 11. Умножение при помощи кругов Последовательность работы умножения двузначного на двузначное число. |
13 х 24 = 312. Чертим круги, так как второй множитель двузначное число, то и два столбца. В первом ряду по одному кругу, во втором ряду по три круга
|
|
|
Второй множитель число 24, то круги, которые в первом столбце делим на две части, а круги, которые во втором столбце делим на четыре части
|
|
|
Проводим прямые и считаем точки.
|
|
| |
|
Ответ записывается следующим образом, смотрим снизу вверх количество точек 12, 2 – последняя цифра результата, один в уме, количество точек во второй области 10 и +1, того 11, 1 пишем и один в уме, количество точек третьей области 2 и +1, того 3. Ответ – 312. [8] Также можно умножить трехзначное число на двузначное. (Приложение 4) Глава 12. Способ умножения Оконешникова Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе. Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35 Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений. В итоге получаем: 078235. Число 78235 и есть результат умножения. Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.[4] Глава 13. Палочки Непера Джон Непер, шотландский математик XVI века – изобретатель счетного прибора, в дальнейшем получившего название «палочки Непера». Умножим числа 2191 и 272 с помощью палочек Непера. Палочки, соответствующие значениям каждого разряда множимого, выкладываются в ряд так, чтобы цифры сверху каждой палочки составляли множимое. Слева прикладывается палочка – указатель строк, по которой выбирают строки, соответствующие разрядам множителя. Суммируем цифры по наклонным полоскам справа налево, при необходимости перенося «в уме» в соседнюю слева полоску единицу или другое число. Результат умножения2191 на 2 – это 4 382. Аналогично находим результат умножения 2 191 на 7. Получаем 15 337. Складываем все полученные результаты, учитывая порядок разряда, получаем искомое произведение.[9] Заключение В процессе исследования изучены разные источники, рассмотрены нестандартные способы умножения и выявлено, что современный используемый алгоритм умножения натуральных чисел - не единственный. Изучив алгоритмы и научившись считать всеми представленными способами, я пришла к выводу, что каждый из способов, несмотря на свою степень сложности и затрат по времени, интересен, но самые простые способы это те, которые мы изучаем в школе – это умножение столбиком и умножение на 9 на пальцах. Может быть потому, что они для нас более привычны. Поэтому гипотеза, выдвинутая вначале исследования, подтвердилась только частично. Из всех найденных мною необычных способов счета более интересным показался японский или китайский способ умножения. Использовать пальцы рук как инструмент при умножении чисел также очень интересно. Заинтересовал меня и итальянский способ умножения. Я научила своих друзей и учащихся разных классов использовать эти способы. По результатам исследования я составила характеристику каждому способу и дала условную оценку всем способам. ( Приложение 5) Во время представления результатов моей работы, я провела несколько мастер - классов в разных классах нашей школы (в 4,7,8 и 9 классах). И уже после занятий попросила всех поучаствовать в анкетировании на степень удовлетворённости знакомства с новыми способами. Результаты опроса показали высокую степень заинтересованности представленным материалом. (Приложение 6) Поэтому можно сделать вывод, что материалы данного исследования имеют большую практическую значимость. Знакомство с новыми нетрадиционными способами умножения будет интересно не только учащимся на уроках математики, а также на математических кружках и при подготовке к мероприятиям недели математики в школе. Изучение содержания разных способов умножения оказалось не только полезным, но и очень увлекательным. Источники https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2016/03/29/proekt-nestandartnye-sposobya-umnozheniya http://dereksiz.org/istoriya-vozniknoveniya-arifmeticheskih-dejstvij.html http://открытыйурок.рф/статьи/652986/ http://iteach.vspu.ru/07-2017/14733/ https://infourok.ru/proekt-na-temu-neobichnie-sposobi-umnozheniya-1497585.html http://www.athens.kiev.ua/egipetskoe-umnozhenie/ https://infourok.ru/proekt_po_teme_nekotorye_nestandartnye_sposoby_scheta_legkie_sposoby_umnozheniya-126504.htm https://kopilkaurokov.ru/matematika/meropriyatia/issliedovatiel-skaia-rabota-po-matiematikie-umnozhieniie-s-uvliechieniiem https://multiurok.ru/index.php/files/priezientatsiia-k-issliedovatiel-skoi-rabotie-razl.html Приложение 1 Анкетирование среди младших школьников Как вы обычно умножаете многозначные числа, если у вас нет калькулятора? Знаете ли вы нестандартные способы умножения? Если да, то какие? Анкетирование среди подростков Как вы обычно умножаете многозначные числа, если у вас нет калькулятора? Знаете ли вы нестандартные способы умножения? Если да, то какие? Анкетирование среди взрослых Как вы обычно умножаете многозначные числа, если у вас нет калькулятора? Знаете ли вы нестандартные способы умножения? Если да, то какие? Приложение 2 Умножение на 9 Человеческая рука является одной из первых счетных машин. Положите обе руки рядом на стол и протяните пальцы. Каждый палец слева направо будет означать соответствующее порядковое число: первый слева — 1, второй — 2, третий — 3, четвертый — 4 и т. д. до десятого, который будет обозначать число 10. Например, нам необходимо умножить 7 на 9. Теперь поднимите седьмой палец. Число пальцев, лежащих налево от поднятого пальца, будет числом десятков произведения, а число пальцев направо — числом единиц. Налево от поднятого пальца лежат 6 пальцев, а направо — 3. Значит, результат умножения 7 на 9 равен 63. Или, например, 3 умножим на 9. Это удивительное на первый взгляд механическое умножение тотчас же станет понятным, если вспомнить, что сумма цифр в каждом произведении чисел таблицы умножения на девять равна девяти, а число десятков в произведении всегда на 1 меньше того числа, которое мы умножаем на 9. Поднятием соответствующего пальца это мы и отмечаем, а, следовательно, и умножаем. Данный способ умножения очень простой и позволяет не заучивать таблицу умножения на 9, а легко посчитать результат на пальцах.[7] Приложение 3 Алгоритм умножения чисел с помощью опорного числа При умножении чисел этим способом пользуются следующими правилами: опорное число записываем слева от произведения в кружке; нарисуем еще два кружка, следующим образом: если множитель меньше опорного числа, то помещаем кружок под ним, если множитель больше опорного числа, то рисуем кружок над ним; разность множителей и опорного числа будем записывать в этих кружках с теми знаками, которые получились; выполним сложение накрест, учитывая правило сложения чисел с разными знаками. Это значит надо прибавить любое из чисел в кружочке к числу не прямо над (под) ним, а к тому, что расположено по диагонали, то есть над (под) другим числом в кружочке. Делать это нужно всего один раз, поэтому выбирайте тот вариант, который вам кажется легче. В любом случае результат получится один и тот же; полученный результат умножаем на опорное число, это будет промежуточный результат, который мы запишем после знака равенства; перемножаем числа в кружочках, учитывая правило перемножения чисел с разными знаками, полученный результат прибавляем к тому, что получилось в 5 пункте, это и будет ответ. [7] Приложение 4 Умножение трехзначного числа на двузначное.
-
123 · 21 = 2583 Чертим круги, так как второй множитель двузначное число, то и два столбца. В первом ряду по одному кругу, во втором ряду по два круга, в третьем ряду по три круга.
|
|
|
2) Проводим прямые и считаем точки.
|
|
Ответ записывается следующим образом, смотрим снизу вверх количество точек 3-последняя цифра результата, количество точек во второй области 8, в третьей области 5, в четвертой области 2. Ответ – 2583.[8] Приложение 5 |
№
|
Название
способа
|
Трудо
ёмкий
|
Требует большой подготовки
|
Насколько быстрый
|
Требует логики
|
Необходимое оборудование
|
Требует дополнительных знаний
|
Моё мнение об этом способе
|
Условная оценка способу
|
|
|
Японский или китайский способ
|
нет
|
нет
|
Достаточно быстрый
|
немного
|
Листок и ручка
|
нет
|
Мне нравится
|
5
|
|
|
Итальянский способ «Сеткой»
|
нет
|
нет
|
Достаточно быстрый
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Подходит для школы
|
4
|
|
|
Индийский способ
|
очень
|
нет
|
Достаточно быстрый
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Тяжелый алгоритм
|
3
|
|
|
Древнерусский способ
|
очень
|
нет
|
Достаточно быстрый
|
нет
|
Пальцы рук
|
Знание таблицы умножения до 5
|
Тяжёлый
алгоритм
|
3
|
|
|
Русский крестьянский способ
|
нет
|
нет
|
Медленный
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Подойдёт для школы
|
4
|
|
|
«Крестиком»
из Древней Греции
|
нет
|
нет
|
Достаточно быстрый
|
да
|
Листок и ручка
|
Знание таблицы умножения
|
Подойдёт для школы
|
4
|
|
|
Египетское умножение
|
нет
|
нет
|
Быстрый
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Подойдёт для школы
|
4
|
|
|
С помощью опорного числа
|
нет
|
нет
|
Медленный
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Интересный
|
4
|
|
|
«Маленький замок» из Средних веков
|
нет
|
нет
|
Достаточно быстрый
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Пригодится для школы
|
4
|
|
|
При помощи кругов
|
да
|
да
|
Медленный
|
нет
|
Листок и ручка
|
Знание таблицы умножения
|
Трудоёмкий
|
3
|
|
|
Способ Оконешникова
|
нет
|
нет
|
Быстрый
|
нет
|
Листок и ручка, таблица
|
Знание таблицы умножения
|
Пригодится для школы
|
4
|
|
|
Палочки Непера
|
нет
|
да
|
Достаточно быстрый
|
нет
|
Палочки Непера, листок и ручка
|
Знание таблицы умножения
|
Трудоёмкий, но интересный
|
4
|
Приложение 6 Анкетирование после проведения мастер – классов Понравилось ли тебе знакомство с новыми способами умножения? Просмотров работы: 99 school-science.ru Способы быстрого устного умножения чисел  Некоторые способы быстрого устного умножения мы уже с Вами разобрали, теперь давайте подробнее разберемся, как быстро умножать числа в уме, используя различные вспомогательные способы. Некоторые способы Вы, возможно, уже знаете, а некоторые из них довольно экзотические, например, древний китайский способ умножения чисел. Некоторые способы быстрого устного умножения мы уже с Вами разобрали, теперь давайте подробнее разберемся, как быстро умножать числа в уме, используя различные вспомогательные способы. Некоторые способы Вы, возможно, уже знаете, а некоторые из них довольно экзотические, например, древний китайский способ умножения чисел. Раскладка по разрядам  Является самым простым приемом быстрого умножения двухзначных чисел. Оба множителя нужно разбить на десятки и единицы, а затем все эти новые числа перемножить друг на друга. Является самым простым приемом быстрого умножения двухзначных чисел. Оба множителя нужно разбить на десятки и единицы, а затем все эти новые числа перемножить друг на друга.
Данный способ требует умения удерживать в памяти одновременно до четырех чисел, и делать с этими числами вычисления. К примеру, нужно перемножить числа 38 и 56. Делаем это следующим образом: 38 * 56 = (30 + 8 ) * (50 + 6) = 30 * 50 + 8 * 50 + 30 * 6 + 8 * 6 = 1500 + 400 + 180 + 48 = 2128 Еще проще будет делать устное умножение двухзначных чисел в три действия. Сначала нужно перемножить десятки, затем прибавить два произведения единиц на десятки, и затем прибавить произведение единиц на единицы. Выглядит это так: 38 * 56 = (30 + 8 ) * (50 + 6) = 30 * 50 + (8 * 50 + 30 * 6) + 8 * 6 = 1500 + 580 + 48 = 2128 Для того, чтобы успешно пользоваться этим способом, нужно хорошо знать таблицу умножения, уметь быстро складывать двухзначные и трехзначные числа, и переключаться между математическими действиями, не забывая промежуточные результаты. Последнее умение достигается с помощью тренировки зрительной памяти и визуализации. Данный способ не самый быстрый и эффективный, потому стоит изучить еще и другие способы устного умножения. Подгонка чисел Можно попробовать привести арифметическое вычисление к более удобному виду. Например, произведение чисел 35 и 49 можно себе представить таким образом: 35 * 49 = (35 * 100) / 2 — 35 = 1715Этот способ может оказаться более эффективным, чем предыдущий, но он не универсальный, и подходит не ко всем случаям. Не всегда можно найти подходящий алгоритм для упрощения задачи. На эту тему вспомнился анекдот про то, как математик проплывал по реке мимо фермы, и заявил собеседникам, что ему удалось быстро подсчитать количество овец в загоне, 1358 овец. Когда его спросили, как ему это удалось, он сказал, что все просто — нужно подсчитать количество ног, и разделить на 4. Визуализация умножения в столбик Этот один из самых универсальных способов устного умножения чисел, развивающий пространственное воображение и память. Для начала следует научиться умножать в столбик в уме двухзначные числа на однозначные. После этого Вы легко сможете умножать двухзначные числа в три действия. Сначала двухзначное число нужно умножить на десятки другого числа, затем умножить на единицы другого числа, и после этого просуммировать полученные числа. Выглядит это таким образом: 38 * 56 = (38 * 5) * 10 + 38 * 6 = 1900 + 228 = 2128 Визуализация с расстановкой чисел Очень интересный способ перемножения двухзначных чисел следующий. Нужно последовательно перемножить цифры в числах, чтобы получились сотни, единицы и десятки. Допустим, Вам нужно умножить 35 на 49. Сначала перемножаете 3 на 4, получаете 12, затем 5 и 9, получаете 45. Записываете 12 и 5 , с пробелом между ними, а 4 запоминаете. Получаете: 12 __ 5 (запоминаете 4). Теперь умножаете 3 на 9, и 5 на 4, и суммируете: 3 * 9 + 5 * 4 = 27 + 20 = 47. Теперь нужно к 47 прибавить 4, которое мы запомнили. Получаем 51. Пишем 1 в середине, а 5 прибавляем к 12, получаем 17. Итого, число, которое мы искали, 1715, оно является ответом: 35 * 49 = 1715Попробуйте таким же образом перемножить в уме: 18 * 34, 45 * 91, 31 * 52. Китайское, или японское, умножение 
В азиатских странах принято умножать числа не в столбик, а рисуя линии. Для восточных культур важно стремление к созерцанию, и визуализации, поэтому, наверное, они и придумали такой красивый метод, позволяющий перемножать любые числа. Сложен этот способ только на первый взгляд. На самом деле, большая наглядность позволяет использовать этот способ гораздо эффективнее, чем умножение в столбик. Кроме того, знание этого древнего восточного етода повышает Вашу эрудицию. Согласитесь, не каждый может похвастаться тем, что знает древнюю систему умножения, которой китайцы пользовались еще 3000 лет назад. Видео о том, как китайцы перемножают числа Более подробные сведения Вы можете получить в разделах "Все курсы" и "Полезности", в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам. Также Вы можете подписаться на блог, и узнавать о всех новых статьях. Это не займет много времени. Просто нажмите на ссылку ниже: Подписаться на блог: Дорога к Бизнесу за Компьютером Проголосуйте и поделитесь с друзьями анонсом статьи на Facebook: pro444.ru Способы умножения. Способы умножения. Солдатова Валерия Александровна 11МБОУ СОШ №3 г.Тосно Неизвестный Евгений Вячеславович 11МБОУ СОШ №3 г.Тосно Текст работы размещён без изображений и формул.Полная версия работы доступна во вкладке "Файлы работы" в формате PDF Введение Вы не сможете выполнить умножения многозначных чисел - хотя бы даже двузначных - если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения. В школе мы изучаем таблицу умножения, а затем учимся умножать числа в столбик. Это не единственный способ умножения. На самом деле, существует несколько десятков способов умножения многозначных чисел. Актуальность: В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» я выбрала тему проекта «Различные способы умножения». Цель: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений. Задачи: Найти и разобрать различные способы умножения. Научиться демонстрировать некоторые способы умножения. Рассказать о новых способах умножения и научить одноклассников ими пользоваться. Основная часть История появления таблицы умножения. При раскопках здания в городе Нара, древней столице Японии, археологами была найдена деревянная табличка с фрагментом таблицы умножения. Из всех табличек, обнаруженных в Японии, найденная – самая древняя. Каким же образом жители Японии впервые узнали о математической «запоминалочки»? Судя по тому, что иероглифы, которыми записаны цифры напоминают китайское письмо, скорее всего, она была просто скопирована из китайского учебника арифметики того времени. А откуда она взялась в Китае? Не исключено, что именно там ее впервые и придумали. Эту версию подтверждает находка, сделанная китайскими археологами на юге страны. Там была обнаружена дощечка, на которой был фрагмент таблицы умножения, возраст которой ученые оценили в 2700 -3000 лет. На основании этой находки ученые Китая предложили гипотезу, согласно которой впервые таблица умножения была составлена в Древнем Китае, а потом вместе с караванами проникли в Индию, а оттуда в страны Передней Азии и Европу. Однако этой версии противоречат многие находки, сделанные ранее. Например, в Индии в свое время были обнаружены более древние варианты таблицы умножения, возраст которых оценивается в 3000-3200 лет. Самые старые в мире таблицы умножения были найдены при раскопках городов Древней Месопотамии. Они были нанесены с помощью клинописи на глиняные таблички, возраст которых составляет 5000 лет. Скорее всего, таблица умножения появилась где-то в тех краях. Хотя не исключено также и то, что данная система устного счета появилась независимо в разных местах. Узнать имя гениального математика, который первым додумался записать результаты умножения в виде таблицы, скорее всего, не удастся. Это пришло в голову сразу нескольким людям. В европейской культуре автором таблицы умножения считается знаменитый греческий математик Пифагор. [1, с.78] Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера. Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть ли не дюжина различных способов умножения и деления - приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия. За тысячелетия развития математики было придумано множество способов умножения чисел, и все эти приемы соперничали друг с другом и усваивались с большим трудом. [2, с.16] Давайте рассмотрим наиболее интересные и простые способы умножения. Способы умножения Русско-крестьянский способ умножения. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоений другого числа. Пример: 32 х 13 |
Множимое =32
|
Множитель = 13
|
|
32
|
13
|
|
16
|
26
|
|
8
|
52
|
|
4
|
104
|
|
2
|
208
|
|
1
|
416
|
Таблица 1. Деление пополам (см. левую половину Табл.1) продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число (правая часть Табл.1). Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение:( 32 х 13 ) = ( 1 х 416 ) [3, с.54] Особо внимательные заметят "А как быть с нечетными числами, которые не кратны 2-м?". Итак, пусть нам необходимо умножить два числа: 987 и 1998. Одно запишем слева, а второе - справа на одной строчке. Левое число будем делить на 2, а правое - умножать на 2 и результаты записывать в столбик. Если при делении возникнет остаток, то он отбрасывается. Операцию продолжаем, пока слева не останется 1. Затем вычеркнем те строчки, в которых слева стоят четные числа и сложим оставшиеся числа в правом столбце. Это и есть искомое произведение. [3, с.67] Дана графическая иллюстрация по данному описанию. ( см. Таблицу 2.) Таблица 2. Квадрат Пифагора. 1 2 3 4 5 6 7 8 9 Это всем известный Квадрат Пифагора, отражающий мировую систему счисления, состоящую из девяти цифр: от 1 до 9. Выражаясь современным языком – это девяти разрядная числовая матрица, в которой цифры, являющиеся основой для дальнейших вычислений любой сложности расположены в порядке возрастания. Квадрат Пифагора называют и Эннеадой, а тройку цифр - триада. Можно рассматривать тройки цифр расположенные по горизонтали (123, 456, 789) и по вертикали(147, 258, 369). Причем, записанные таким образом, тройки цифр начинают обозначать уже особые числа, подчиняющиеся законам математической пропорции и гармонии. Вспомним главное правило древнеегипетской математики, в котором сказано, что умножение производится при помощи удвоения и сложения полученных результатов; то есть каждое удвоение есть сложение числа с самим собой. Поэтому интересно посмотреть на результат подобного удвоения цифр и чисел, но полученному современным методом складывания « в столбик», известному даже в начальных классах школы. Это будет напоминать египетскую систему счисления, по сути, с разницей в том, что все цифры либо числа записываются в один столбик (без указания того или иного действия в соседнем столбике - как у египтян). [4, с.97] Начнем с цифр, составляющих Квадрат Пифагора: от 1 – до 9. 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 3 6 9 12 15 18 21 24 27 4 8 12 16 20 24 28 32 36 5 10 15 20 25 30 35 40 45 6 12 18 24 30 36 42 48 54 7 14 21 28 35 42 49 56 63 8 16 24 32 40 48 56 64 72 9 18 27 36 45 54 63 72 81 10 20 30 40 50 60 70 80 90 Цифра 1: обычный последовательный ряд цифр. Цифра 9: левый столбик - четкий восходящий ряд («поток»). правый столбик - четкий нисходящий ряд последовательных цифр. Условимся называть восходящим ряд, значения чисел в котором увеличиваются сверху вниз ; в нисходящем же – наоборот: уменьшаются значения чисел сверху вниз. Цифра 2: в правом столбике повторяются четные цифры 2,4,6,8 («в периоде»). Цифра 8: такой же повтор - только в обратном порядке- 8,6,4,2. Цифры 4 и 6: четные цифры «в периоде» 4,8,2,6 и 6,2,8,4. Цифра 5: подчиняется правилу сложения цифры 5- чередование 5 и 0. Цифра 3: правый столбик - нисходящий ряд уже не цифр, а чисел, образующих тройки вертикальных рядов в квадрате Пифагора- 369, 258, 147. Причем, отсчет идет «из правого угла квадрата» или справа налево. Здесь также действует принятое выше правило восходящего - нисходящего ряда. Но восходящий ряд – это движение от тройки чисел 147 до тройки 369; нисходящий - от 369 до 147. Цифра 7: восходящий ряд чисел 147,258,369 из «левого угла» или слева направо. Впрочем, все зависит от того, как изображена сама девятиразрядная числовая матрица - где поставить цифру 1. Китайский способ умножения. Такой прием напоминает умножение столбиком, но проводится довольно долго. Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок: Этот рисунок состоит из 10 линий (количество может быть любым) Эти линии обозначают число 24 (2 линии, отступ, 4 линии) А эти линии обозначают число 13 (1 линия, отступ, 3 линии) Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом: (пересечения на рисунке указаны точками) Количество пересечений: Верхний левый край: 2 Нижний левый край: 6 Верхний правый: 4 Нижний правый: 12 1) Пересечения в верхнем левом крае (2) – первое число ответа 2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа 3) Пересечения в нижнем правом крае (12) – третье число ответа. Получается: 2; 10; 12. Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему. 3(2+1)1(0+1)2 Ответ: 312 [5, с.48] Итальянский способ умножения. В Италии, а также во многих странах Востока, этот способ приобрел большую известность. [5, с.74] Использование приема: Например, умножим 6827 на 345. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте. Умножаем число каждого ряда последовательно на числа каждой колонки. т.е. 6*3 = 18. Записываем 1 и 8 8*3 = 24. Записываем 2 и 4 Если при умножении получается однозначное число, записываем вверху 0, а внизу это число. (Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6) Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали. Ответ: 2355315. Таблица Оконешникова. Рис.1. Таблица Оконешникова Умножение не стоит на месте, о чем доказывает новый способ умножения, который разработал Василий Иванович Оконешников. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе и «теперь ребята смогут умножать и складывать в уме не только единицы, десятки, но также миллионы, триллионы и даже, не пугайтесь, секстиллионы с квадриллионами»При этом каждая кнопка делится еще на 9 квадратов, в которой записываются результаты перемножения числа данной кнопки на числа от одного до девяти, т.е. получаем своеобразную таблицу умножения. Данный метод имеет ограничение - умножение делается на однозначное число. Например, найдем произведение чисел 148 и 4. Для этого обратимся к квадрату соответствующему четверке, выбираем числа, соответствующие цифрам числа по порядку: единице, четверке, восьмерке. Получаем: 04 16 32. Левую цифру (в нашем примере - ноль) оставляем без изменений, а следующие складываем попарно: четверку с единицей, шестерку с тройкой.. Последняя цифра также без изменений. 0(4 + 1)(6+3)2 = 0592. Число 592 и есть результат умножения. Произведя расчет по методу Василия Ивановича Оконешникова при умножении многозначного числа на однозначное, этот метод достаточно прост и быстр, если имеется готовая таблица в уме или перед глазами. [8, с.32] Индийский способ умножения. В древней Индии применяли два способа умножения: сетки и галеры. На первый взгляд они кажутся очень сложными, но если следовать шаг за шагом в предлагаемых упражнениях, то можно убедиться, что это довольно просто. Умножаем, например, числа 6827 и 345: 1. Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте. В предложенном примере можно использовать одну из этих сеток. Сетка 1 Сетка 2 2. Выбрав сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Посмотри на этой схеме, как пишется произведение в соответствующей клетке. Сетка 1 3. Посмотри, как выглядит сетка со всеми заполненными клетками. Сетка 1 4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали. Сетка1 Посмотри, как из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315, которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315. [8, с.65] Египетский способ умножения. Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное перемножение на второй множитель (см. пример). Этот метод можно и сегодня встретить в очень отдаленных регионах. Разложение. Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число. Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу значений: 1 x 2 = 2 2 x 2 = 4 4 x 2 = 8 8 x 2 = 16 16 x 2 = 32 Пример разложения числа 25: Кратный множитель для числа «25» — это 16; 25 — 16 = 9. Кратный множитель для числа «9» — это 8; 9 — 8 = 1. Кратный множитель для числа «1» — это 1; 1 — 1 = 0. Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1. [9, с.28] Пример: умножим «13» на «238» . Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: ✔ 1 х 238 = 238 ✔ 4 х 238 = 952 ✔ 8 х 238 = 1904 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 =1904 + 952 + 238 = 3094. Заключение Существует много различных, забавных и интересных способов умножения чисел, но не все они удобны в использовании. Из всех найденных мною необычных способов счета более интересным и простым показался мне «Итальянский способ». Я показал некоторые способы умножения своим одноклассникам, и многие очень заинтересовались необычными вычислениями. Работая над этим проектом, я пришла к выводу, что самый простой и привычный способ умножения, это тот, который мы изучаем в школе. А чтобы пользоваться этим способом, нужно всем знать наизусть таблицу умножения! Список литературы и Интернет - ресурсы 1.1. Арутюнян Е., Левитас Г. Занимательная математика. - М.: АСТ - ПРЕСС, 1999. - 368 с.1.2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. - ЛКИ ,2012.-208 с.1.3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140 с.1.4. Ликум А. Все обо всем. Т. 2. - М.: Филологическое общество «Слово», 1993. - 512 с.1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.1.6. Перельман Я.И. Занимательная арифметика. - М.: Русанова, 1994 – 205с.1.7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с. 1.8. Савин А.П. Математические миниатюры. Занимательная математика для детей. - М.: Детская литература, 1998 - 175 с.1.9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.2. Другие источники информацииИнтернет – ресурсы: 2.1. Корнеев А.А. Феномен русского умножения. История. [Электронный ресурс] Приложение 1 Анкетирование Мною было проведено анкетирование учащихся 5а класса, в котором приняли участие 25 человек. На основании анкетирования выявлено, что все опрошенные умеют умножать традиционным способом, а вот о нетрадиционных способах умножения большинство ребят не знают. И есть желающие познакомиться с ними. Вопросы в анкете были следующие: Когда была неделя математики в нашей школе, видели ли вы мою стенгазету о разных способах умножения? Рис.2. Круговая диаграмма. Опрос учащихся к 1-му вопросу Ответ: да – 20 человек, нет – 5 человек. Знаете ли вы нетрадиционные способы умножения? Приведите пример. Рис.3. Круговая диаграмма. Опрос учащихся к 2-му вопросу Ответ: знают – 7 человек, не знают – 18 человек. Хотели бы вы научиться нетрадиционным способам умножения? Рис.3. Круговая диаграмма. Опрос учащихся к 3-му вопросу Ответ: хотят – 19 человек, не хотят – 6 человек. Приложение 2 Сравнение результатов по вычислению примеров (по эффективности затраченного времени) |
Время, за которое мне и моим одноклассникам удалось решить один и тот же пример разными способами
|
| |
Китайский способ
|
Таблица Оконешникова
|
Итальянский способ
|
Столбик
|
|
Я
|
56 секунд
|
30 секунд
|
25 секунд
|
8 секунд
|
|
Ученик №1
|
58 секунд
|
32 секунд
|
28 секунд
|
10 секунд
|
|
Ученик №2
|
1 минута 6 секунд
|
50 секунд
|
42 секунды
|
10 секунд
|
|
Ученик №3
|
1 минута 10 секунд
|
56 секунд
|
48 секунды
|
11 секунд
|
|
Ученик №4
|
1 минута 25 секунд
|
1 минута
|
55 секунд
|
12 секунд
|
Вывод: самым эффективным способом умножения является умножение столбиком. Приложение 3 Моя работа на неделе математики в школе Приложение 4 Памятка для учащихся Просмотров работы: 39 school-science.ru Необычные способы умножения | Социальная сеть работников образованияСлайд 1 Необычные способы умножения Работу выполнила у ченица 8 класса А МОУ СОШ №1 г.Можайска Шкиндер ОльгаСлайд 2 Цель работы: Показать необычные методы умножения Научить одноклассников новым видам умножения Слайд 3 Введение В истории математики известно около 30 способов умножения. Метод умножения «столбик» мы изучаем в школе. Интересно , это самый легкий способ? Слайд 4 Немного из истории. Не так давно при раскопках здания в городе Нара, древней столице Японии, археологами была найдена деревянная табличка с фрагментом таблицы умножения. Предполагается, что подобные таблицы были необходимы императорским чиновникам для того, чтобы легче освоить одно из основных арифметических действий. Иероглифы, которыми записаны цифры, чрезвычайно напоминают принятые при китайской династии Тан . Поэтому, скорее всего, таблица умножения была просто скопирована из китайского учебника арифметики того времени. Слайд 5 Древнерусский способ Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9 . Пальцы рук здесь служили вспомогательным вычислительным устройством. Для этого на одной руке вытягивали столько пальцев, на сколько, первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались. Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56. Так можно вычислять произведение любых однозначных чисел, больше 5 Слайд 6 Японский метод Шаг1. Первое число 15 Рисуем первую цифру-одной линией Рисуем вторую цифру-пятью линиями Шаг2-второе число 23 Рисуем первую цифру-двумя линиями Вторую цифру-тремя линиями Шаг3-считать количество точек в группах Шаг4-результат 345 Слайд 8 В Италии, а также во многих странах Востока, этот способ приобрел большую известность. Использование приема: Например, умножим 6827на 345. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте. Умножаем число каждого ряда последовательно на числа каждой колонки . 6*3 = 18. Записываем 1 и 8 8*3 = 24. Записываем 2 и 4 Если при умножении получается однозначное число, записываем вверху 0, а внизу это число. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали. Ответ:2355315 Слайд 9 . Индийский способ умножения. Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец. Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила: Правило 1. Единицы первого произведения следует писать в той же колонке, что и множитель, то есть в данном случае под 9. Правило 2. Последующее произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения. Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С). Затем складываем цифры в колонках и получаем ответ: 72956. Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат. Слайд 10 Выводы Простые способы это те, которые мы изучаем в школе, а может быть, мы просто к ним привыкли Из всех рассмотренных необычных способов счета более интересным показался японский способ умножения .. Самым простым показался метод , который использовали русские крестьяне. Слайд 11 Использованные материалы http://ss.gym5cheb.ru/p22aa1. html http://skolkobudet.ru/publ/4-1-0-5 Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с . Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 12 с. Слайд 12 Спасибо за внимание nsportal.ru Решётчатое умножение | Наука и жизнь Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа. В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков. Умножение способом решётки. Иллюстрация из первой печатной книги по арифметике. 1487 год. Палочки Непера. Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год. Джон Непер (1550—1617). Модель счётной машины Шиккарда. Это не дошедшее до нас вычислительное устройство изготовлено изобретателем в 1623 году и описано им годом позже в письме Иоганну Кеплеру. Вильгельм Шиккард (1592—1635). ‹ › Наследие индусов — способ решётки Индусы, с давних времён знавшие десятичную систему счисления, предпочитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, — умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Способ решётки именовали также индийским, мусульманским или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского — «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.
Суть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, — по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально — число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
 Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Почему способ решётки приводит к правильному ответу? В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 + 90 + 6 и 70 + 3.
 Как видим, в первой косой полосе стоят единицы, во второй — десятки, в третьей — сотни и т.д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:
Как видим, в первой косой полосе стоят единицы, во второй — десятки, в третьей — сотни и т.д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:
 Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так: Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:
296 x 73 = (200 + 90 + 6) x (70 + 3) = 14 000 + 6300 + 420 + 600 + 270 + 18 = 10 000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70 + 20 + 10) + 8 = 21 608.
Палочки Непера
Умножение способом решётки лежит в основе простого и оригинального счётного прибора — палочек Непера. Его изобретатель Джон Непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.
Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней — число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.
Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие — с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.
 Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
296 x 73 = 20 720 + 888 = 21 608.
Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
296 x 73 = 20 720 + 888 = 21 608.
Палочки Непера применялись и для более сложных операций — деления и извлечения квадратного корня. Этот счётный прибор не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения чисел, например с повторяющимися цифрами, нужны были несколько комплектов палочек. Но такая проблема решалась заменой линеек вращающимися цилиндрами с нанесённой на поверхность каждого из них таблицей умножения в том же виде, как её представил Непер. Вместо одного набора палочек получалось сразу девять.
Подобные ухищрения в самом деле ускоряли и облегчали расчёты, однако не затрагивали главный принцип работы прибора Непера. Так способ решётки обрел вторую жизнь, продлившуюся ещё несколько столетий.
Машина Шиккарда
Учёные давно задумывались над тем, как переложить непростую вычислительную работу на механические устройства. Первые успешные шаги в создании счётных машин удалось осуществить только в XVII столетии. Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
По сути, машина Шиккарда представляет собой шестиразрядный механический калькулятор, выполняющий сложение, вычитание, умножение и деление чисел. В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.
В работе счётная машина Шиккарда очень проста. Чтобы узнать, чему равно произведение 296 x 73, нужно установить цилиндры в положение, при котором в верхнем ряду окошек появится первый множитель: 000296. Произведение 296 x 3 получим, открыв окошки третьего ряда и просуммировав увиденные цифры, как в способе решётки. Точно так же, открыв окошки седьмого ряда, получим произведение 296 x 7, к которому припишем справа 0. Остаётся только сложить найденные числа на суммирующем устройстве.
Придуманный некогда индусами быстрый и надёжный способ умножения многозначных чисел, много веков применявшийся при расчётах, ныне, увы, забыт. А ведь он мог бы выручить нас и сегодня, если бы под рукой не оказалось столь привычного всем калькулятора.
www.nkj.ru
|
