Проект "Великие математики древности". Древние математики
Древнегреческий математик и философ. Выдающиеся древнегреческие математики и их достиженияДревние греки внесли огромный вклад в развитие точных наук: математики, астрономии, физики. Другие народы в то время тоже обладали определённым багажом знаний. Но если египтяне и вавилоняне довольствовались уже открытыми и исследованными областями, то греки пошли ещё дальше. Они не останавливались на достигнутом и открывали новые горизонты в разных сферах жизни. 
Математика в Древней ГрецииЭта наука одна из самых давних и востребованных. Безусловно, греки способствовали развитию культуры и географии, логики и экономики. Их философская школа была настолько развитой, что и поныне удивляет современников утверждениями и открытиями. Но математике отведена отдельная ниша в этой сложной системе научных знаний. Многие достижения в области арифметики обязаны дискуссиям, которые были так популярны у греков. Люди собирались на площади, спорили и таким образом приходили к единственно правильному решению. "В споре рождается истина" – эта догма дошла до нас именно с тех времён. Любой древнегреческий математик пользовался почётом и уважением. Выведенные теоремы и формулы, тяжело понимаемые простыми людьми, возносили его на вершину пьедестала, в ряды других великих умов. Развитие математики как науки во многом обязано Архимеду, Пифагору, Евклиду и другим личностям, труды и открытия которых положены в основу современного курса алгебры и геометрии в школах и университетах. Пифагор и его школа
Это древнегреческий математик, философ, политик, общественный и религиозный деятель. Родился он примерно в 580 году до нашей эры на острове Самос, вследствие чего в народе его прозвали Самосским. Согласно легенде, Пифагор был очень красивым и статным мужчиной. Он не уставал изучать все новое и неизведанное, его образование было поистине элитным. Учился юноша не только у себя на родине, но также в Индии, Египте и Вавилоне. Пифагор, древнегреческий математик, покровительствовал рабовладельцам и аристократии. Идеалист до мозга костей, в Кротоне он основал собственную школу, которая была одновременно и религиозной, и политической структурой. Чёткая организация бытовой жизни, строгие правила и каноны – главные её особенности. Например, члены сообщества не могли владеть частной собственностью, придерживались вегетарианской диеты и обязывались не открывать посторонним людям учения своего преподавателя. Когда демократия докатилась до Кротона, Пифагор и его последователи бежали в Метапонт. Но народное восстание бушевало и в этом городе. В одной из драк 90-летний математик погиб. Вместе с ним перестала существовать и его знаменитая школа. 
Открытия ПифагораИзвестно наверняка, что именно его авторству принадлежит описание целых чисел, их свойств и пропорций. Также он был одним из первых учёных, кто утверждал, что Земля круглая, что планеты имеют не такую траекторию движения, как звёзды. Все эти идеи положены в основу знаменитого гелиоцентрического учения Коперника. Поскольку вся жизнь учёного была окружена тайной, до наших дней дошло не много интересных фактов о его деятельности. Некоторые сомневаются, что знаменитую теорему доказал именно он. По некоторым данным, знали её и многие другие древние народы ещё задолго до рождения математика. Древнегреческий философ и математик обладал множеством способностей, и не только в области точных наук. Его имя и деятельность окутаны мифами и легендами, а также мистикой. Считалось, что Пифагор управляет духами с загробного мира, понимает язык животных, общается с ними, задаёт полёту птиц нужное ему направление, умеет предсказывать будущее. Также ему приписывали знахарские способности. Архимед: основные трудыЭто один из самых ярких представителей той эпохи, знаменитый учёный, философ, математик и изобретатель. Родился он в 287 году до нашей эры в Сиракузе. В этом небольшом городке он прожил почти всю жизнь, тут писал свои известные трактаты и испытывал новые механизмы. Его отцом был придворный астроном Фидий, поэтому обучение Архимеда проходило на высшем уровне. Он имел доступ к самой лучшей библиотеке того времени, в читальных залах которой провёл не один день. 
До наших дней сохранилось несколько математических трудов учёного. Условно их можно подразделить на три основные группы. - Работы, посвящённые объёмам и площадям криволинейных тел и фигур. В них содержится множество доказанных теорем.
- Геометрический анализ гидростатических и статических задач. Это исследования про равновесие фигур, про положение тела в воде и так далее.
- Другие математические работы. Например, про исчисление песчинок, механическое доказательство теорем.
Архимед погиб во время захвата Сиракузы римскими войсками. Он был так увлечён чертежом новой геометрической задачи, что не заметил воина, который подошёл сзади. Солдат убил учёного, не зная, что военачальник отдал приказ сохранить жизнь известному математику и философу. Вклад Архимеда в развитие точных наук Каждый ребёнок знаком с этим выдающимся деятелем ещё со школы. Кто же он, древнегреческий математик, воскликнувший "Эврика"? Ответ на этот вопрос прост – это Архимед. Согласно легенде, царь поручил ему выяснить - из чистого золота сделана его корона или ювелир схитрил, разбавив его другими металлами. Думая над этой задачей, Архимед лёг в ванну, наполненную водой. И тут ему пришло в голову потрясающее открытие: количество жидкости, которая переливается за край ванны, равно объёму воды, вытесненной его телом. Сделав этот вывод, он и закричал всем нам известное слово "эврика". Математик древнегреческий с этим возгласом выскочил из бани и побежал домой, в чём мать родила, спеша записать своё открытие. Каждый ребёнок знаком с этим выдающимся деятелем ещё со школы. Кто же он, древнегреческий математик, воскликнувший "Эврика"? Ответ на этот вопрос прост – это Архимед. Согласно легенде, царь поручил ему выяснить - из чистого золота сделана его корона или ювелир схитрил, разбавив его другими металлами. Думая над этой задачей, Архимед лёг в ванну, наполненную водой. И тут ему пришло в голову потрясающее открытие: количество жидкости, которая переливается за край ванны, равно объёму воды, вытесненной его телом. Сделав этот вывод, он и закричал всем нам известное слово "эврика". Математик древнегреческий с этим возгласом выскочил из бани и побежал домой, в чём мать родила, спеша записать своё открытие.
Кроме того, Архимед за две тысячи лет до открытия интегралов сумел рассчитать площадь параболического сегмента. Он открыл миру число "пи", доказав, что соотношение диаметра круга и длины его окружности всегда одинаково для любой такой геометрической фигуры. Он создал так называемый Архимедов винт – прообраз современных воздушных и корабельных винтов. Среди его достижений метательные и подъёмные машины. Секрет создания его "зажигательного зеркала", при помощи которого были уничтожены вражеские корабли, до сих пор не раскрыли современные исследователи. Евклид
Большую часть своего времени он работал над музыкальными произведениями, раскрывал секреты механики и физики, изучал астрономию. Но часть своих трудов всё же посвятил математике: довёл до ума несколько доказательств и теорем. Его вклад в развитие этой науки сложно переоценить, так как работы Евклида стали основой для других учёных, живших на много столетий позже его. Как зовут древнегреческого математика, написавшего известный математический сборник "Начала", состоящий из 15 книг? Конечно, Евклид. Он сумел сформулировать основные положения геометрии, доказал важные теоремы: про сумму углов треугольника и теорему Пифагора. Также его имя связывают с учением про построение правильных многогранников, которыми сегодня восхищается каждый юный математик на уроках геометрии. Евклид открыл метод исчерпывания. Его взяли на вооружение Ньютон и Лейбниц, открыв способы исчисления: интегральный и дифференциальный. Фалес
Этот древнегреческий математик родился примерно в 625 году до нашей эры. Долгое время он жил в Египте и тесно общался с правителем этой страны, царём Амазисом. Легенда гласит, что однажды он изумил фараона, измерив высоту пирамиды только по величине её тени. Фалес считается родоначальником греческой науки, одним из семи мудрецов, изменивших основы знаний. Историки уверены, что Фалес первым доказал основные теоремы геометрии. Например, о том, что вписанный в полуокружность угол всегда прямой, диаметр делит круг на две одинаковые части, у равнобедренного треугольника углы при основании равны, все вертикальные углы идентичны и так далее. Фалес вывел формулу, согласно которой треугольники всегда будут одинаковыми, если у них идентичны одна грань и углы, прилегающие к ней. Он научился определять расстояние до плывущих вдали кораблей при помощи условных треугольников. Кроме того, он сделал пару открытий в астрономической науке, определив точное время солнцестояний и равноденствий. Также он первым безошибочно просчитал продолжительность года. 
ЭратосфенЭто достаточно разносторонний деятель. Увлекался изучением космоса, географическими открытиями, исследовал речь, языковые обороты и исторические события. В сфере алгебры и геометрии он известен нам как древнегреческий математик, сделавший открытие в системе простых чисел. Он создал "Решето Эратосфена", интересный метод, который доныне изучают в школах. Благодаря ему можно отсеивать простые числа из общего ряда. Цифры не вычёркивали, как сегодня, а прокалывали на общем рисунке. Отсюда и название – "решето". Эратосфен сумел самостоятельно сконструировать мезолябий – прибор для решения на основе законов механики делосской задачи про удвоение куба. Он смог первым измерить Землю. Просчитав длину части земного меридиана, он вывел окружность планеты - 39 тысяч 960 километров. Ошибся только на каких-то незначительных 300 километров. Эратосфен действительно заметная фигура того времени, без его достижений математика не могла бы существовать в своём привычном виде. Герон Этот древнегреческий математик жил в первом веке до нашей эры. Данные приблизительные, так как точных свидетельств про его жизнь дошло до наших дней очень мало. Известно, что Герон увлекался законами физики, механики, ценил достижения инженерной науки. Это он первым создал автоматические двери, кукольный театр, турбину паруса, древний "таксометр" – прибор для измерения дороги, автомат и самозаряжающийся арбалет. Этот древнегреческий математик жил в первом веке до нашей эры. Данные приблизительные, так как точных свидетельств про его жизнь дошло до наших дней очень мало. Известно, что Герон увлекался законами физики, механики, ценил достижения инженерной науки. Это он первым создал автоматические двери, кукольный театр, турбину паруса, древний "таксометр" – прибор для измерения дороги, автомат и самозаряжающийся арбалет.
Много его трудов было посвящено и математике. Он вывел новые геометрические формулы, разработал методы исчисления геометрических фигур. Герон создал знаменитую формулу, названную его именем, при помощи которой можно вычислить площадь треугольника, если знать длину всех его сторон. После себя он оставил много рукописных книг, в которых были отображены не только его труды, но и исследования других учёных. И в этом его самая большая заслуга. Благодаря этим записям мы сегодня знаем про Архимеда, Пифагора и других известных математиков, ставших символами той эпохи и прославивших Древнюю Грецию на весь античный мир. fb.ru Великие математики и их открытияМатематика появилась одновременно со стремлением человека изучить мир вокруг себя. Изначально она входила в состав философии - матери наук - и не была выделена как отдельная дисциплина наравне с той же астрономией, физикой. Однако с течением времени ситуация изменилась. В данной статье мы выясним, кто они - великие математики, список которых уже перемахнул за сотню. Выделим основные имена. НачалоЗнаний у людей накапливалось все больше, в итоге произошло разделение точных и естественных наук. После официального "рождения" каждая из них пошла своим путем, развиваясь, укрепляя фундамент теорией, подкрепленной практикой. Казалось бы, какая практика может быть у математики, самой абстрактной из наук? Этот предмет способен описать абсолютно все процессы, происходящие на нашей планете и за ее пределами, а знание природы явления позволяет делать выводы и строить прогнозы. Отсюда можно сделать вывод, что все науки связаны между собой, наиболее очевидна эта зависимость между математикой и физикой. Поэтому в большинстве случаев великие математики и физики составляют одну группу ученых. Посудите сами - как можно описать что-то, не получив при этом обоснования? Человеческая история - это не только покорение новых территорий и войны, в которых сильные мира сего преследуют в первую очередь свои интересы, но и бесконечные научные выкладки, призванные объяснить, показать, познать и выяснить перспективу завтрашнего дня. В данной статье мы рассмотрим тех, кто внес весомый вклад в создание настоящего. Кто они, великие математики прошлого, что подготовили почву для современных открытий? ПифагорКогда упоминаются великие математики, большинству людей на ум первым делом приходит именно это имя. Никто доподлинно не знает, что из фактов его биографии является правдой, а что – вымыслом, так как имя обросло массой легенд. За период жизни принят диапазон дат от 570 до 490 года до н. э. К сожалению, письменных работ после него не осталось, однако принято считать, что именно с его благословения были сделаны многие открытия того времени. Однако мы укажем лишь те достижения, что неоспоримо являются плодами его трудов: - Геометрия – знаменитая теорема, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Не стоит забывать и таблицу Пифагора, по которой школьники начальной школы изучают принцип перемножения натуральных чисел. Также он вывел метод построения некоторых многоугольников.
- География – великий математик Пифагор первый предположил, что планета Земля является круглой.
- Астрономия – гипотеза о существовании внеземных цивилизаций.
ЕвклидЭтому древнегреческому математику современная наука обязана геометрией. Евклид родился в 365 году до н. э. в Афинах и в течение 65 лет (до конца жизни, по сути) проживал в Александрии. Его можно смело назвать революционером среди научных деятелей того времени, так как он проделал огромную работу по объединению всего накопленного опыта прошлых лет в одну ровную, логичную систему без "дыр" и противоречий. Этот великий ученый (физик и математик) создал трактат "Начала", который включал в себя более дюжины томов! Помимо этого, из-под его руки вышли работы, описывающие распространение луча света по прямой. Теория Евклида хороша тем, что он в ней оттолкнулся от абстрактного "может быть", приведя ряд постулатов (утверждений, что не требуют доказательств), и уже от них, пользуясь сухой математической логикой, вывел стройную систему существующей ныне геометрии. Франсуа ВиетВеликие математики и их открытия тоже зависят от воли случая. Это доказал господин Виет (годы жизни – 1540-1603), который проживал во Франции и служил при королевском дворе сначала адвокатом, а потом и советником монарха. Когда вместо Генриха III на трон взошел Генрих IV, Франсуа поменял род деятельности. Ряд «Мировые великие математики», список которых не мал, пополнился новым именем благодаря войне Франции с Испанией. Последняя в своей переписке применяла сложный шифр, который невозможно было расшифровать. Таким образом, враги французской короны могли вести свободную переписку на территории противника без страха быть пойманными. Перепробовав все методы, король обратился к Виету. В течение полумесяца математик работал без отдыха, пока не добился нужного результата. Благодаря этому математик вновь стал личным советником, но уже нового короля. Параллельно с этим Испания стала терпеть поражение за поражением, не понимая, в чем дело. Наконец, правда всплыла наружу, и инквизиция заочно вынесла приговор Франсуа к казни, но так и не исполнила его. На своей новой должности советник получил возможность погрузиться в математику, отдавая всего себя любимому делу, как и все великие люди. О математике и Виете говорили с недоумением, акцентируя внимание на том, что он успевает совмещать увлечение с юридической практикой. Среди достижений Виета числятся: - Буквенные обозначения в алгебре. Французский математик заменил параметры и часть коэффициентов буквами, сократив выражения в несколько раз. Эта мера сделала алгебраические высказывания более простыми и доступными для понимания, параллельно с этим облегчив дальнейшие выводы. Этот шаг стал революционным, так как облегчил дорогу идущим позади. Поистине великий математик Пифагор оставил свое детище в надежных руках. Идеология завтрашнего дня передана полностью.
- Вывод теории решения уравнений до четвертой степени включительно.
- Вывод формулы имени себя, по которой и по сей день находят корни квадратных уравнений.
- Вывод и обоснование первого в истории науки бесконечного произведения.
Леонард ЭйлерСветило науки с удивительной судьбой. Рожденный в Швейцарии (1707 год), он может смело входить в список "Великие русские математики", так как наиболее плодотворно работал и нашел последнее пристанище в России (1783 год). Период его работ и открытий связан именно с нашей страной, в которую он переехал в 1726 году по приглашению академии наук в Санкт-Петербурге. За полтора десятилетия он написал массу трудов как по математике, так и по физике. В общей сложности им было сделано около 9 сотен сложнейших выводов, обогативших науку того времени. К закату жизни Леонарда Эйлера, вопреки правилам (но с одобрения французского правительства), Парижская академия наук сделала его девятым членом, тогда как по правилам их должно быть восемь. Только великие математики могли быть удостоены такой чести, так как любая научная организация педантична, когда дело касается соблюдения правил. Среди открытий Леонарда Эйлера необходимо отметить: - Объединение математики как науки. До XVIII века, который по праву считается периодом триумфа Эйлера, все дисциплины были разрознены. Алгебра, математический анализ, геометрия, теория вероятности и т. д. существовали сами по себе, не пересекаясь. Он собрал из них стройную, логичную систему, которая и сейчас преподносится в учебных заведениях без изменений.
- Вывод числа е, которое примерно равно 2,7. Как вы можете заметить, великие ученые-математики зачастую обретают бессмертие в своих работах, не миновала чаша сия и Эйлера – первая буква фамилии дала название этому иррациональному числу, без которого не существовало бы натурального логарифма.
- Первую формулировку теории интегрирования с указанием методов, которые в ней применяются. Введение двойных интегралов.
- Основание и распространение диаграмм Эйлера – лаконичных и наглядных графиков, которые показывают связь множеств вне зависимости от их происхождения. Например, благодаря им можно показать, что бесконечное множество натуральных чисел включено в бесконечное множество рациональных чисел и так далее.
- Написание революционных для того времени трудов по дифференциальному исчислению.
- Дополнение элементарной геометрии, выведенной еще Евклидом. Например, он вывел и доказал, что все высоты треугольника пересекаются в одной точке.
Галилео ГалилейЭтот научный деятель, проживший всю жизнь в Италии (с 1564 по 1642 год), знаком каждому школьнику. Период его деятельности пришелся на смутную пору, что проходила под знаком инквизиции. Любое инакомыслие каралось, наука преследовалась, так как противоречила утверждениям теологов. Никто и ничто не могло быть описано, ибо на все воля Божья. Именно математик Галилей, согласно легенде, стал автором фразы «И всё-таки она вертится!», после того как отрекся от своих слов о том, что Земля вращается вокруг Солнца, а не наоборот. Шаг этот был обусловлен борьбою за жизнь, так как инквизиция сочла ересью его гипотезу, в которой участники вращения поменялись местами. Священнослужители не могли допустить того, чтобы Земля как творенье Божье перестала быть центром всего. Однако его труды данной гипотезой не ограничились, ибо в историю он вошел как великий физик и математик. Галилей: - путем эмпирических исследований отверг утверждение Аристотеля, в котором говорилась о том, что скорость падения тела прямо пропорциональна его весу;
- вывел парадокс имени себя, в котором количество натуральных чисел равно количеству их же квадратов, притом что большая часть чисел квадратами не является;
- написал труд «Рассуждение об игре в кости», в котором рассмотрел эталонную с точки зрения теории вероятностей задачу с выводом и обоснованием.
Андрей Николаевич КолмогоровКогда упоминаются великие математики России, одним из первых на ум приходит именно этот научный деятель. Алексей Николаевич Колмогоров родился весной 1903 года в городе Тамбове. Начальное образование он получил дома, после чего поступил в частную гимназию. Уже там были отмечены его удивительные способности в области точных наук. В силу ряда обстоятельств его семья была вынуждена переехать в Москву, где их и застала Гражданская война. Несмотря ни на что, Колмогоров поступил в Московский университет на факультет математики. Успехи молодого студента на выбранном поприще были столь велики, что он без особых усилий смог досрочно сдать экзамены, не отрываясь от своего основного увлечения – теории вероятности. В научных изданиях стали появляться труды Андрея Николаевича, начиная с 1923 года, а ведь ему на тот момент едва минуло 20 лет. Методично добиваясь желаемого, математик уже в 1939 году стал академиком. Он проработал всю жизнь в Москве и умер осенью 1987 года, похоронен на Новодевичьем кладбище. К его весомым работам можно отнести: - Усовершенствование методики преподавания математики в начальных и средних школах. Великие математики и их открытия мирового масштаба важны, однако не менее ценной и нужной является работа по подготовке молодого поколения будущих научных деятелей. Всем известно, что основы закладываются в раннем детстве.
- Развитие математических методов и перенос их из абстрактных областей в прикладные. Иными словами, благодаря трудам Андрея Николаевича математика прочно вошла в естественные науки.
- Вывод принятых мировым научным сообществом аксиом элементарной теории вероятностей. Последняя характеризуется тем, что описывает конечное число событий.
Николай Иванович ЛобачевскийЭтот научный деятель, как и все великие русские математики, с детства проявлял недюжинные способности в области точных наук. Николай Иванович Лобачевский родился в 1793 году в одной из губерний России. В возрасте 7 лет вместе с семьей переехал в Казань, где и прожил всю свою жизнь. Скончался он в возрасте 63 лет, увековечив свое имя на века работой, что дополнила классическую геометрию Евклида. Он ввел несколько уточнений в привычную систему, доказав ряд утверждений, например, о том, что параллельные прямые пересекаются на бесконечности. Его работа определяется в плоскости, которая характеризуется скоростями, близкими к скорости света. Казалось бы, в чем смысл открытия для того времени? Теорию находили спорной, возмутительной, однако с течением времени великие ученые-математики признали, что работа Лобачевского приоткрыла дверь в будущее. Огюстен Луи КошиИмя этого математика известно каждому студенту, так как он успел отметиться как в общем курсе высшей математики, так и в ее более узких направлениях, например, в математическом анализе. Огюстен Луи Коши (годы жизни – 1789-1857) по праву может считаться отцом математического анализа. Именно он довел до ума все то, что пребывало в подвешенном состоянии, не имея ни определения, ни обоснования. Благодаря его трудам появились такие столпы дисциплины, как непрерывность, предел, производная и интеграл. Также Коши показал сходимость ряда и его радиус, дал математическое обоснование дисперсии в оптике. Вклад Коши в становлении современной математики был настолько масштабен, что его имя заняло почетное место на первом этаже Эйфелевой башни - именно там в хронологическом порядке перечислены ученые (в том числе великие математики). Список этот служит своеобразным памятником науке и по сей день. ИтогИз века в век математика привлекала ученых своей неестественностью, которая удивительным образом могла описать все то, что происходит в мире вокруг нас. Пифагор утверждал, что в основе всего лежит число. Практически все, что происходит с человеком и внутри человека, оно может описать. Галилей говорил, что математика - это язык природы. Вдумайтесь. Величина, что имеет искусственную природу, описывает все естественное. Имена великих математиков - это не просто перечень людей, которые увлекались своим делом, расширяя и углубляя научную базу. Это звенья, которые способны связать настоящее и будущее, показать человечеству перспективу. Однако это палка о двух концах, так как обилие информации дает больше рычагов для воздействия. Знания - это власть. Бездумное злоупотребление способно погубить то, что так тщательно изучалось и собиралось по крупицам. Осознание этого первостепенно, наука должна идти во благо. Великие люди о математике говорят с бесконечным уважением, так как это пропуск в завтрашний день. fb.ru Математика в древности Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Дальнейшее развитие математики началось примерно в 3000 до н.э. благодаря вавилонянам и египтянам. ВАВИЛОНИЯ И ЕГИПЕТ Вавилония. Источником наших знаний о вавилонской цивилизации служат хорошо сохранившиеся глиняные таблички, покрытые т.н. клинописными текстами, которые датируются от 2000 до н.э. и до 300 н.э. Математика на клинописных табличках в основном была связана с ведением хозяйства. Арифметика и нехитрая алгебра использовались при обмене денег и расчетах за товары, вычислении простых и сложных процентов, налогов и доли урожая, сдаваемой в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи возникали в связи со строительством каналов, зернохранилищ и другими общественными работами. Очень важной задачей математики был расчет календаря, поскольку календарь использовался для определения сроков сельскохозяйственных работ и религиозных праздников. Деление окружности на 360, а градуса и минуты на 60 частей берут начало в вавилонской астрономии. Вавилоняне создали и систему счисления, использовавшую для чисел от 1 до 59 основание 10. Символ, обозначавший единицу, повторялся нужное количество раз для чисел от 1 до 9. Для обозначения чисел от 11 до 59 вавилоняне использовали комбинацию символа числа 10 и символа единицы. Для обозначения чисел начиная с 60 и больше вавилоняне ввели позиционную систему счисления с основанием 60. Существенным продвижением стал позиционный принцип, согласно которому один и тот же числовой знак (символ) имеет различные значения в зависимости от того места, где он расположен. Примером могут служить значения шестерки в записи (современной) числа 606. Однако нуль в системе счисления древних вавилонян отсутствовал, из-за чего один и тот же набор символов мог означать и число 65 (60 + 5), и число 3605 (602 + 0 + 5). Возникали неоднозначности и в трактовке дробей. Например, одни и те же символы могли означать и число 21, и дробь 21/60 и (20/60 + 1/602). Неоднозначность разрешалась в зависимости от конкретного контекста. Вавилоняне составили таблицы обратных чисел (которые использовались при выполнении деления), таблицы квадратов и квадратных корней, а также таблицы кубов и кубических корней. Им было известно хорошее приближение числа . Клинописные тексты, посвященные решению алгебраических и геометрических задач, свидетельствуют о том, что они пользовались квадратичной формулой для решения квадратных уравнений и могли решать некоторые специальные типы задач, включавших до десяти уравнений с десятью неизвестными, а также отдельные разновидности кубических уравнений и уравнений четвертой степени. На глиняных табличках запечатлены только задачи и основные шаги процедур их решения. Так как для обозначения неизвестных величин использовалась геометрическая терминология, то и методы решения в основном заключались в геометрических действиях с линиями и площадями. Что касается алгебраических задач, то они формулировались и решались в словесных обозначениях. Около 700 до н.э. вавилоняне стали применять математику для исследования движений Луны и планет. Это позволило им предсказывать положения планет, что было важно как для астрологии, так и для астрономии. В геометрии вавилоняне знали о таких соотношениях, например, как пропорциональность соответствующих сторон подобных треугольников. Им была известна теорема Пифагора и то, что угол, вписанный в полуокружность – прямой. Они располагали также правилами вычисления площадей простых плоских фигур, в том числе правильных многоугольников, и объемов простых тел. Число Пи вавилоняне считали равным 3. Египет. Наше знание древнеегипетской математики основано главным образом на двух папирусах, датируемых примерно 1700 до н.э. Излагаемые в этих папирусах математические сведения восходят к еще более раннему периоду – ок. 3500 до н.э. Египтяне использовали математику, чтобы вычислять вес тел, площади посевов и объемы зернохранилищ, размеры податей и количество камней, требуемое для возведения тех или иных сооружений. В папирусах можно найти также задачи, связанные с определением количества зерна, необходимого для приготовления заданного числа кружек пива, а также более сложные задачи, связанные с различием в сортах зерна; для этих случаев вычислялись переводные коэффициенты. Но главной областью применения математики была астрономия, точнее расчеты, связанные с календарем. Календарь использовался для определения дат религиозных праздников и предсказания ежегодных разливов Нила. Однако уровень развития астрономии в Древнем Египте намного уступал уровню ее развития в Вавилоне. Древнеегипетская письменность основывалась на иероглифах. Система счисления того периода также уступала вавилонской. Египтяне пользовались непозиционной десятичной системой, в которой числа от 1 до 9 обозначались соответствующим числом вертикальных черточек, а для последовательных степеней числа 10 вводились индивидуальные символы. Последовательно комбинируя эти символы, можно было записать любое число. С появлением папируса возникло так называемое иератическое письмо-скоропись, способствовавшее, в свою очередь, появлению новой числовой системы. Для каждого из чисел от 1 до 9 и для каждого из первых девяти кратных чисел 10, 100 и т.д. использовался специальный опознавательный символ. Дроби записывались в виде суммы дробей с числителем, равным единице. С такими дробями египтяне производили все четыре арифметические операции, но процедура таких вычислений оставалась очень громоздкой. Геометрия у египтян сводилась к вычислениям площадей прямоугольников, треугольников, трапеций, круга, а также формулам вычисления объемов некоторых тел. Надо сказать, что математика, которую египтяне использовали при строительстве пирамид, была простой и примитивной. Задачи и решения, приведенные в папирусах, сформулированы чисто рецептурно, без каких бы то ни было объяснений. Египтяне имели дело только с простейшими типами квадратных уравнений и арифметической и геометрической прогрессиями, а потому и те общие правила, которые они смогли вывести, были также самого простейшего вида. Ни вавилонская, ни египетская математики не располагали общими методами; весь свод математических знаний представлял собой скопление эмпирических формул и правил. Хотя майя, жившие в Центральной Америке, не оказали влияния на развитие математики, их достижения, относящиеся примерно к 4 в., заслуживают внимания. Майя, по-видимому, первыми использовали специальный символ для обозначения нуля в своей двадцатиричной системе. У них были две системы счисления: в одной применялись иероглифы, а в другой, более распространенной, точка обозначала единицу, горизонтальная черта – число 5, а символ обозначал нуль. Позиционные обозначения начинались с числа 20, а числа записывались по вертикали сверху вниз.. ГРЕЧЕСКАЯ МАТЕМАТИКА Классическая Греция. С точки зрения 20 в. родоначальниками математики явились греки классического периода (6–4 вв. до н.э.). Математика, существовавшая в более ранний период, была набором эмпирических заключений. Напротив, в дедуктивном рассуждении новое утверждение выводится из принятых посылок способом, исключавшим возможность его неприятия. Настаивание греков на дедуктивном доказательстве было экстраординарным шагом. Ни одна другая цивилизация не дошла до идеи получения заключений исключительно на основе дедуктивного рассуждения, исходящего из явно сформулированных аксиом. Одно из объяснений приверженности греков методам дедукции мы находим в устройстве греческого общества классического периода. Математики и философы (нередко это были одни и те же лица) принадлежали к высшим слоям общества, где любая практическая деятельность рассматривалась как недостойное занятие. Математики предпочитали абстрактные рассуждения о числах и пространственных отношениях решению практических задач. Математика делилась на арифметику – теоретический аспект и логистику – вычислительный аспект. Заниматься логистикой предоставляли свободнорожденным низших классов и рабам. Греческая система счисления была основана на использовании букв алфавита. Аттическая система, бывшая в ходу с 6–3 вв. до н.э., использовала для обозначения единицы вертикальную черту, а для обозначения чисел 5, 10, 100, 1000 и 10 000 начальные буквы их греческих названий. В более поздней ионической системе счисления для обозначения чисел использовались 24 буквы греческого алфавита и три архаические буквы. Кратные 1000 до 9000 обозначались так же, как первые девять целых чисел от 1 до 9, но перед каждой буквой ставилась вертикальная черта. Десятки тысяч обозначались буквой М (от греческого мириои – 10 000), после которой ставилось то число, на которое нужно было умножить десять тысяч. Дедуктивный характер греческой математики полностью сформировался ко времени Платона и Аристотеля. Изобретение дедуктивной математики принято приписывать Фалесу Милетскому (ок. 640–546 до н.э.), который, как и многие древнегреческие математики классического периода, был также философом. Высказывалось предположение, что Фалес использовал дедукцию для доказательства некоторых результатов в геометрии, хотя это сомнительно. Другим великим греком, с чьим именем связывают развитие математики, был Пифагор (ок. 585–500 до н.э.). Полагают, что он мог познакомиться с вавилонской и египетской математикой во время своих долгих странствий. Пифагор основал движение, расцвет которого приходится на период ок. 550–300 до н.э. Пифагорейцы создали чистую математику в форме теории чисел и геометрии. Целые числа они представляли в виде конфигураций из точек или камешков, классифицируя эти числа в соответствии с формой возникающих фигур («фигурные числа»). Слово «калькуляция» (расчет, вычисление) берет начало от греческого слова, означающего «камешек». Числа 3, 6, 10 и т.д. пифагорейцы называли треугольными, так как соответствующее число камешков можно расположить в виде треугольника, числа 4, 9, 16 и т.д. – квадратными, так как соответствующее число камешков можно расположить в виде квадрата, и т.д. Из простых геометрических конфигураций возникали некоторые свойства целых чисел. Например, пифагорейцы обнаружили, что сумма двух последовательных треугольных чисел всегда равна некоторому квадратному числу. Они открыли, что если (в современных обозначениях) n2 – квадратное число, то n2 + 2n +1 = (n + 1)2. Число, равное сумме всех своих собственных делителей, кроме самого этого числа, пифагорейцы называли совершенным. Примерами совершенных чисел могут служить такие целые числа, как 6, 28 и 496. Два числа пифагорейцы называли дружественными, если каждое из чисел равно сумме делителей другого; например, 220 и 284 – дружественные числа (и здесь само число исключается из собственных делителей). Для пифагорейцев любое число представляло собой нечто большее, чем количественную величину. Например, число 2 согласно их воззрению означало различие и потому отождествлялось с мнением. Четверка представляла справедливость, так как это первое число, равное произведению двух одинаковых множителей. Пифагорейцы также открыли, что сумма некоторых пар квадратных чисел есть снова квадратное число. Например, сумма 9 и 16 равна 25, а сумма 25 и 144 равна 169. Такие тройки чисел, как 3, 4 и 5 или 5, 12 и 13, называются пифагоровыми числами. Они имеют геометрическую интерпретацию, если два числа из тройки приравнять длинам катетов прямоугольного треугольника, то третье число будет равно длине его гипотенузы. Такая интерпретация, по-видимому, привела пифагорейцев к осознанию более общего факта, известного ныне под названием теоремы Пифагора, согласно которой в любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Рассматривая прямоугольный треугольник с единичными катетами, пифагорейцы обнаружили, что длина его гипотенузы равна , и это повергло их в смятение, ибо они тщетно пытались представить число в виде отношения двух целых чисел, что было крайне важно для их философии. Величины, непредставимые в виде отношения целых чисел, пифагорейцы назвали несоизмеримыми; современный термин – «иррациональные числа». Около 300 до н.э. Евклид доказал, что число несоизмеримо. Пифагорейцы имели дело с иррациональными числами, представляя все величины геометрическими образами. Если 1 и считать длинами некоторых отрезков, то различие между рациональными и иррациональными числами сглаживается. Произведение чисел и есть площадь прямоугольника со сторонами длиной и .Мы и сегодня иногда говорим о числе 25 как о квадрате 5, а о числе 27 – как о кубе 3. Древние греки решали уравнения с неизвестными посредством геометрических построений. Были разработаны специальные построения для выполнения сложения, вычитания, умножения и деления отрезков, извлечения квадратных корней из длин отрезков; ныне этот метод называется геометрической алгеброй. Приведение задач к геометрическому виду имело ряд важных последствий. В частности, числа стали рассматриваться отдельно от геометрии, поскольку работать с несоизмеримыми отношениями можно было только с помощью геометрических методов. Геометрия стала основой почти всей строгой математики по крайней мере до1600. И даже в 18 в., когда уже были достаточно развиты алгебра и математический анализ, строгая математика трактовалась как геометрия, и слово «геометр» было равнозначно слову «математик». Именно пифагорейцам мы во многом обязаны той математикой, которая затем была систематизированно изложена и доказана в Началах Евклида. Есть основания полагать, что именно они открыли то, что ныне известно как теоремы о треугольниках, параллельных прямых, многоугольниках, окружностях, сферах и правильных многогранниках. Одним из самых выдающихся пифагорейцев был Платон (ок. 427–347 до н.э.). Платон был убежден, что физический мир постижим лишь посредством математики. Считается, что именно ему принадлежит заслуга изобретения аналитического метода доказательства. (Аналитический метод начинается с утверждения, которое требуется доказать, и затем из него последовательно выводятся следствия до тех пор, пока не будет достигнут какой-нибудь известный факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических построений. Величайшим из греческих математиков классического периода, уступавшим по значимости полученных результатов только Архимеду, был Евдокс (ок. 408–355 до н.э.). Именно он ввел понятие величины для таких объектов, как отрезки прямых и углы. Располагая понятием величины, Евдокс логически строго обосновал пифагорейский метод обращения с иррациональными числами. Работы Евдокса позволили установить дедуктивную структуру математики на основе явно формулируемых аксиом. Ему же принадлежит и первый шаг в создании математического анализа, поскольку именно он изобрел метод вычисления площадей и объемов, получивший название «метода исчерпывания». Этот метод состоит в построении вписанных и описанных плоских фигур или пространственных тел, которые заполняют («исчерпывают») площадь или объем той фигуры или того тела, которое является предметом исследования. Евдоксу же принадлежит и первая астрономическая теория, объясняющая наблюдаемое движение планет. Предложенная Евдоксом теория была чисто математической; она показывала, каким образом комбинации вращающихся сфер с различными радиусами и осями вращения могут объяснить кажущиеся нерегулярными движения Солнца, Луны и планет. Около 300 до н.э. результаты многих греческих математиков были сведены в единое целое Евклидом, написавшим математический шедевр Начала. Из немногих проницательно отобранных аксиом Евклид вывел около 500 теорем, охвативших все наиболее важные результаты классического периода. Свое сочинение Евклид начал с определения таких терминов, как прямая, угол и окружность. Затем он сформулировал десять самоочевидных истин, таких, как «целое больше любой из частей». И из этих десяти аксиом Евклид смог вывести все теоремы. Для математиков текст Начал Евклида долгое время служил образцом строгости, пока в 19 в. не обнаружилось, что в нем имеются серьезные недостатки, такие как неосознанное использование несформулированных в явном виде допущений. Аполлоний (ок. 262–200 до н.э.) жил в александрийский период, но его основной труд выдержан в духе классических традиций. Предложенный им анализ конических сечений – окружности, эллипса, параболы и гиперболы – явился кульминацией развития греческой геометрии. Аполлоний также стал основателем количественной математической астрономии. Александрийский период. В этот период, который начался около 300 до н.э., характер греческой математики изменился. Александрийская математика возникла в результате слияния классической греческой математики с математикой Вавилонии и Египта. В целом математики александрийского периода были больше склонны к решению чисто технических задач, чем к философии. Великие александрийские математики – Эратосфен, Архимед, Гиппарх, Птолемей, Диофант и Папп – продемонстрировали силу греческого гения в теоретическом абстрагировании, но столь же охотно применяли свой талант к решению практических проблем и чисто количественных задач. Эратосфен (ок. 275–194 до н.э.) нашел простой метод точного вычисления длины окружности Земли, ему же принадлежит календарь, в котором каждый четвертый год имеет на один день больше, чем другие. Астроном Аристарх (ок. 310–230 до н.э.) написал сочинение О размерах и расстояниях Солнца и Луны, содержавшее одну из первых попыток определения этих размеров и расстояний; по своему характеру работа Аристарха была геометрической. Величайшим математиком древности был Архимед (ок. 287–212 до н.э.). Ему принадлежат формулировки многих теорем о площадях и объемах сложных фигур и тел, вполне строго доказанные им методом исчерпывания. Архимед всегда стремился получить точные решения и находил верхние и нижние оценки для иррациональных чисел. Например, работая с правильным 96-угольником, он безукоризненно доказал, что точное значение числа p находится между 31/7 и 310/71. Архимед доказал также несколько теорем, содержавших новые результаты геометрической алгебры. Ему принадлежит формулировка задачи о рассечении шара плоскостью так, чтобы объемы сегментов находились между собой в заданном отношении. Архимед решил эту задачу, отыскав пересечение параболы и равнобочной гиперболы. Архимед был величайшим математическим физиком древности. Для доказательства теорем механики он использовал геометрические соображения. Его сочинение О плавающих телах заложило основы гидростатики. Согласно легенде, Архимед открыл носящий его имя закон, согласно которому на тело, погруженное в воду, действует выталкивающая сила, равная весу вытесненной им жидкости, во время купания, находясь в ванной, и не в силах совладать с охватившей его радостью открытия, выбежал обнаженный на улицу с криком: «Эврика!» («Открыл!») Во времена Архимеда уже не ограничивались геометрическими построениями, осуществимыми только с помощью циркуля и линейки. Архимед использовал в своих построениях спираль, а Диоклес (конец 2 в. до н.э.) решил проблему удвоения куба с помощью введенной им кривой, получившей название циссоиды. В александрийский период арифметика и алгебра рассматривались независимо от геометрии. Греки классического периода имели логически обоснованную теорию целых чисел, однако александрийские греки, восприняв вавилонскую и египетскую арифметику и алгебру, во многом утратили уже наработанные представления о математической строгости. Живший между 100 до н.э. и 100 н.э. Герон Александрийский трансформировал значительную часть геометрической алгебры греков в откровенно нестрогие вычислительные процедуры. Однако, доказывая новые теоремы евклидовой геометрии, он по-прежнему руководствовался стандартами логической строгости классического периода. Первой достаточно объемистой книгой, в которой арифметика излагалась независимо от геометрии, было Введение в арифметику Никомаха (ок. 100 н.э.). В истории арифметики ее роль сравнима с ролью Начал Евклида в истории геометрии. На протяжении более 1000 лет она служила стандартным учебником, поскольку в ней ясно, четко и всеобъемлюще излагалось учение о целых числах (простых, составных, взаимно простых, а также о пропорциях). Повторяя многие пифагорейские утверждения, Введение Никомаха вместе с тем шло дальше, так как Никомах видел и более общие отношения, хотя и приводил их без доказательства. Знаменательной вехой в алгебре александрийских греков стали работы Диофанта (ок. 250). Одно из главных его достижений связано с введением в алгебру начал символики. В своих работах Диофант не предлагал общих методов, он имел дело с конкретными положительными рациональными числами, а не с их буквенными обозначениями. Он заложил основы т.н. диофантова анализа – исследования неопределенных уравнений. Высшим достижением александрийских математиков стало создание количественной астрономии. Гиппарху (ок. 161–126 до н.э.) мы обязаны изобретением тригонометрии. Его метод был основан на теореме, утверждающей, что в подобных треугольниках отношение длин любых двух сторон одного из них равно отношению длин двух соответственных сторон другого. В частности, отношение длины катета, лежащего против острого угла А в прямоугольном треугольнике, к длине гипотенузы должно быть одним и тем же для всех прямоугольных треугольников, имеющих один и тот же острый угол А. Это отношение известно как синус угла А. Отношения длин других сторон прямоугольного треугольника получили название косинуса и тангенса угла А. Гиппарх изобрел метод вычисления таких отношений и составил их таблицы. Располагая этими таблицами и легко измеримыми расстояниями на поверхности Земли, он смог вычислить длину ее большой окружности и расстояние до Луны. По его расчетам, радиус Луны составил одну треть земного радиуса; по современным данным отношение радиусов Луны и Земли составляет 27/1000. Гиппарх определил продолжительность солнечного года с ошибкой всего лишь в 61/2 минуты; считается, что именно он ввел широты и долготы. Греческая тригонометрия и ее приложения в астрономии достигли пика своего развития в Альмагесте египтянина Клавдия Птолемея (умер в 168 н.э.). В Альмагесте была представлена теория движения небесных тел, господствовавшая вплоть до 16 в., когда ее сменила теория Коперника. Птолемей стремился построить самую простую математическую модель, сознавая, что его теория – всего лишь удобное математическое описание астрономических явлений, согласованное с наблюдениями. Теория Коперника одержала верх именно потому, что как модель она оказалась проще. Упадок Греции. После завоевания Египта римлянами в 31 до н.э. великая греческая александрийская цивилизация пришла в упадок. Цицерон с гордостью утверждал, что в отличие от греков римляне не мечтатели, а потому применяют свои математические знания на практике, извлекая из них реальную пользу. Однако в развитие самой математики вклад римлян был незначителен. Римская система счисления основывалась на громоздких обозначениях чисел. Главной ее особенностью был аддитивный принцип. Даже вычитательный принцип, например, запись числа 9 в виде IX, вошел в широкое употребление только после изобретения наборных литер в 15 в. Римские обозначения чисел применялись в некоторых европейских школах примерно до 1600, а в бухгалтерии и столетием позже. ИНДИЯ И АРАБЫ Преемниками греков в истории математики стали индийцы. Индийские математики не занимались доказательствами, но они ввели оригинальные понятия и ряд эффективных методов. Именно они впервые ввели нуль и как кардинальное число, и как символ отсутствия единиц в соответствующем разряде. Махавира (850 н.э.) установил правила операций с нулем, полагая, однако, что деление числа на нуль оставляет число неизменным. Правильный ответ для случая деления числа на нуль был дан Бхаскарой (р. в 1114), ему же принадлежат правила действий над иррациональными числами. Индийцы ввели понятие отрицательных чисел (для обозначения долгов). Самое раннее их использование мы находим у Брахмагупты (ок. 630). Ариабхата (р. 476) пошел дальше Диофанта в использовании непрерывных дробей при решении неопределенных уравнений. Наша современная система счисления, основанная на позиционном принципе записи чисел и нуля как кардинального числа и использовании обозначения пустого разряда, называется индо-арабской. На стене храма, построенного в Индии ок. 250 до н.э., обнаружено несколько цифр, напоминающих по своим очертаниям наши современные цифры. Около 800 индийская математика достигла Багдада. Термин «алгебра» происходит от начала названия книги Аль-джебр ва-л-мукабала (Восполнение и противопоставление), написанной в 830 астрономом и математиком аль-Хорезми. В своем сочинении он воздавал должное заслугам индийской математики. Алгебра аль-Хорезми была основана на трудах Брахмагупты, но в ней явственно различимы вавилонское и греческое влияния. Другой выдающийся арабский математик Ибн аль-Хайсам (ок. 965–1039) разработал способ получения алгебраических решений квадратных и кубических уравнений. Арабские математики, в их числе и Омар Хайям, умели решать некоторые кубические уравнения с помощью геометрических методов, используя конические сечения. Арабские астрономы ввели в тригонометрию понятие тангенса и котангенса. Насирэддин Туси (1201–1274) в Трактате о полном четырехугольнике систематически изложил плоскую и сферическую геометрии и первым рассмотрел тригонометрию отдельно от астрономии. И все же самым важным вкладом арабов в математику стали их переводы и комментарии к великим творениям греков. Европа познакомилась с этими работами после завоевания арабами Северной Африки и Испании, а позднее труды греков были переведены на латынь. Литература: Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959 Юшкевич А.П. История математики в средние века. М., 1961 Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. М., 1986 Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989 Источник: http://www.krugosvet.ru s30556663155.mirtesen.ru 20 математиков, которые изменили мир Перед тем, как ученые предложат новые лекарства или инженеры придумают усовершенствованные технологии, они исписывают доски числами, используя понятия, которые ввели математики иногда за несколько столетий перед этим. Многие школьники не согласятся с этим, но исследования ни в какой другой области не сыграли большей роли в изменении хода истории, чем математические исследования. К сожалению, вклад математиков в историю остается часто практически неоцененным. Мы изменим это прямо сейчас. Мы определили 20 математиков, ответственных за то, каким является современный мир. Уильям Плейфэр (William Playfair), изобретатель диаграмм  Изменение торгового баланса за день 1786 г. Уильям Плейфэр, шотландский инженер, считается основателем графической статистики. Кроме этого значительного достижения, он был в разные периоды своей жизни банкиром, бухгалтером, журналистом, экономистом, участвовал в штурме Бастилии. Трудно переоценить значение его работ. Он изобрел линейчатый график, секторную диаграмму в круге и круговую диаграмму. Он также впервые использовал временную линию. Вы, возможно, знакомы с его трудами. Джеймс Максвелл (James Maxwell), первый фотограф в цвете  Джеймс Максвелл Максвелл — шотландский математик, основатель классической электромагнитной теории. Эта теория дала векам исследований в области магнетизма, электричества и оптики единую теоретическую основу. Максвелл был первым, кто продемонстрировал, что электричество распространяется в пространстве со скоростью света. Насколько важны его исследования? У Эйнштейна на столе стояла фотография Максвелла в рамке рядом с фотографиями Майкла Фарадея и Исаака Ньютона. Он был первым, кто начал развивать цветную фотографию. Установление связи света и электромагнитных явлений считается одним из величайших достижений современной физики. Максвелл во многом продвинулся в этой области. Алан Тьюринг (Alan Turing), кодировщик Второй мировой войны  Статуя Тьюринга в Блетчли парке Алан Тьюринг — британский математик, который считается отцом информатики. Его работы заложили основы для создания ПК, вы, видимо, об этом знаете. Тьюринг очень известен благодаря своим заслугам во время Второй мировой войны. Работая в знаменитом Блетчли-парке, Тьюринг был одним из самых главных разработчиков методов взлома немецкого кода Enigma. Он создал метод, с помощью которого “Бомба’’ (Bombe) — грандиозная электромеханическая машина, построенная Союзниками — смогла взломать Enigma в промышленных масштабах, позволяя читать почти все немецкие сообщения. Таким образом, Тьюринг является одним из основателей современного криптоанализа, и именно он по праву выиграл одну из самых важных частей битвы за Атлантику, помогая Союзникам. Пьер-Симон Лаплас (Pierre-Simon Laplace), основатель статистики  Портрет Лапласа, Sophie Feytaud, 1841 Маркиз де Лаплас сыграл решающую роль в развитии математической астрономии и, самое главное, статистики. Лаплас одним из первых предположил существование черных дыр. Он сыграл решающую роль в систематизации теории вероятностей, заложив основу для того, что сейчас называется байесовской статистикой. Он одним из первых изучал скорость звука. Томас Байес (Thomas Bayes), продвинувший статистику  Томас Байес Томас Байес, пресвитерианский священник, заложил основу байесовской статистики. Существенно, что статистические методы позволяют сделать некоторые выводы о существующей ситуации по результатам статистических тестов. Теорема Байеса дает возможность найти условные вероятности. Не вдаваясь в излишние подробности, скажем, что эта теорема является важной в области статистики вывода. Чарльз Бэббидж (Charles Babbage), изобретатель компьютера  Чарльз Бэббидж, The Illustrated London News, 1871 Чарльз Бэббидж — английский математик и изобретатель, который считается “отцом компьютера’’ за изобретение первого механического вычислительного устройства. Разностная машина Бэббиджа не была закончена при его жизни, но работа, сделанная им, послужила толчком развитию этой области. Проблемы с финансированием мешали Бэббиджу, но его труды были продолжены и стали признанными. Позже он разработал Аналитическую Машину (Analytical Engine), которая теоретически могла быть запрограммирована с перфокарт. Ада Лавлейс (Ada Lovelace), первый программист  Портрет ады Лавлейс, Margaret Sarah Carpenter, 1836 Работавшая с Чарльзом Бэббиджем графиня Ада Лавлейс, по мнению некоторых, является первым программистом в мире. Ада была дочерью поэта лорда Байрона и переписывалась с Бэббиджем в то время, когда он пытался построить свои разностную и аналитическую машины. Она считала себя “аналитиком’’, а Бэббидж описал ее как “чаровницу чисел’’. Она умерла в возрасте всего лишь тридцати шести лет, но ее переводы и заметки сегодня являются как историческими записями исследований Бэббиджа, так и одним из первых обсуждением компьютерного программирования. Давид Гильберт (David Hilbert), покровитель учителей математики  Давид Гильберт Давид Гильберт, кроме своего огромного вклада в функциональный анализ, может также считаться покровителем учителей математики. Гильберт является одним из основателей теории доказательств, он был лидером в области математики. Одним из его самых важных достижений было создание в 1900 году легендарного списка из 23 нерешенных проблем. Эти задачи стали программными для всей математики 20-го века. Благодаря им Гильберт вдохновил и мотивировал поколения математиков. Евклид Александрийский (Εὐκλείδης) и его доказательства  Евклид Евклид, древнегреческий математик, жил во времена правления Птолемея I (323-283 гг. до н.э.). Он является автором книги “Начала’’, служившей основным учебником по математике до начала 19-го века. Он создал евклидову геометрию, и, хотя, возможно, Евклид не самым очевидным образом повлиял на современную эпоху, однако он, конечно, ответственен за большую часть элементарной математики, которая привела к современному состоянию мира. Евклид был одним из первых, кто формализовал математические доказательства — основной метод изложения дисциплины. Исаак Ньютон (Issac Newton), основоположник математического анализа  Портрет Ньютона, Godfrey Kneller , 1689 Этот список был бы неполным без упоминания сэра Исаака Ньютона — английского светила научной революции. Ньютон разработал начала физики, научные методы, теорию всемирного тяготения, и дифференциальное исчисление. Он усовершенствовал телескоп, развил ньютоновскую механику. Законы Ньютона хорошо известны сегодня даже людям за пределами научного сообщества. Его влияние на современную физику почти невозможно переоценить. Готфрид Лейбниц (Gottfried Leibniz), всегда в тени Ньютона  Портрет Лейбница, Christoph Bernhard Francke, 1700 Немецкий математик Готфрид Лейбниц изобрел исчисление бесконечно малых независимо от англичанина сэра Исаака Ньютона. Его обозначения по-прежнему широко используются сегодня. Он был заядлым изобретателем механических калькуляторов и добавил действия умножения и деления для калькулятора Паскаля. В конце 17-го века он доработал двоичную систему счисления, что позволило построить цифровые компьютеры несколько веков спустя. Неисправимый оптимист, Лейбниц придумал фразу “лучший из всех возможных миров’’. Жозеф Лагранж (Joseph Lagrange), упростивший работы Ньютона  Портрет Лагранжа, Unknown Artist, 18th Century Мало кто из математиков сделал столько, сколько это удалось Лагранжу. Его наследие так велико, что его имя — одно из 72 имен, начертанных на Эйфелевой башне среди имен наиболее выдающихся французских ученых и инженеров 18-19 веков. Он похоронен в Пантеоне — усыпальнице великих французов. Лагранж по существу создал теорию уравнений в частных производных (в 1772 — 1785 гг.). Сегодня эта теория используется для моделирования процессов, связанных с теплопередачей, звуком, процессов электродинамики и других трудно моделируемых процессов. Кроме того, он полностью переформулировал и упростил уравнения классической механики Ньютона. Наконец, он также решил задачу трех тел — одну из самых сложных проблем в физике (примеч. Лагранж нашел решение в двух частных случаях). Блез Паскаль (Blaise Pascal), изобретатель первого калькулятора  Портрет Паскаля, Anonymous Portrait Блез Паскаль — французский математик и физик, живший в 17 веке. Он прояснил понятия давления и вакуума. Паскаль изобрел первую версию рулетки и создал гидравлический пресс. Он придумал шприц. Также он сделал вклад в развитие начал теории вероятностей и актуарной науки, и создал первый механический калькулятор. Джон фон Нейман (John von Neumann), разработчик цифровых компьютеров  Джон фон Ньюман, Los Alamos I.D. picture Американец венгерского происхождения Джон фон Нейман — один из величайших математиков своего времени. Кроме большого вклада в различные разделы чистой математики он проделал большую работу в прикладных областях. Фон Нейман первым в США предложил концепцию взаимного гарантированного уничтожения во время холодной войны. Кроме того, он выдвинул идею самовоспроизводящихся автоматов. Он является ключевой фигурой в развитии цифровой вычислительной техники. Джон фон Нейман разработал методику завершения термоядерной реакции. Леонард Эйлер (Leonhard Euler), математик с воображением  Леонард Эйлер Швейцарский математик, который провел большую часть своей жизни в России, Леонард Эйлер считается выдающимся математиком своего времени. Эйлер был первым, кто ввел понятие функции, что само по себе является огромным достижением. Это заложило основу для развития всей математики. Он был первым, обозначившим буквой “e’’ основание натурального логарифма, первым, кто использовал “i’’ для мнимой единицы, и именно он начал использовать букву “сигма’’ как знак суммы. Он ввел формулу Эйлера — тригонометрическое равенство, и вывел тождество Эйлера,  . Он оказал глубокое влияние на математику. . Он оказал глубокое влияние на математику. Даниил Бернулли (Daniel Bernoulli), создавший основы аэродинамики  Даниил Бернулли Даниила Бернулли, швейцарского математика, помнят за его вклад в механику жидкости и работы в области статистики и теории вероятностей. Он был одним из многих членов семьи Бернулли, внесших значительный вклад в математику. Даниил Бернулли одним из первых попытался разработать кинетическую теорию газов. Принцип Бернулли является важнейшим в аэродинамических исследованиях. Он был пионером в медицине, где применял имеющиеся статистические данные для описания вспышки оспы, произошедшей в 1766 году. Он построил первоначальную теорию неприятия риска и полезности, применимую в экономике и финансовой деятельности. Карл Фридрих Гаусс (Carl Freidrich Gauss) стоит за всем, что мы знаем о статистике  Карл Фиридрих Гаусс, Astronomische Nachrichten, 1828 Гаусс считается одним из самых выдающихся математиков в истории. Немецкий вундеркинд, Гаусс одолжил свое имя огромному количеству открытий, называемых его именем даже после его смерти. Напоминающая колокол кривая нормального распределения — центральный элемент современной статистики. Это распределение иногда называют распределением Гаусса. Гаусс также интересовался дифференциальными уравнениями, которые широко применяются в современной технике. Он разработал теорему, в которой установлены важные свойства кривизны. Позднее, в 1833 году, он совместно с Вильгельмом Вебером построил первый электромагнитный телеграф. Жозеф Фурье (Joseph Fourier) объяснил парниковый эффект  Жозеф Фурье Жозеф Фурье стал сиротой, когда ему было восемь лет, во время Французской революции он работал в локальном революционном комитете. Фурье участвовал в экспедиции Наполеона в Египет и сыграл определенную роль в переводе надписи на Розеттском камне. Он внес вклад в термодинамику, многомерный анализ и вывел дифференциальное уравнение теплопроводности в частных производных, которое сегодня изучается в элементарных курсах физики. В 1820 году он одним из первых признал влияние атмосферы на сохранение тепла, что в настоящее время известно как парниковый эффект. Теодор фон Карман (Theodore von Kármán), вертолет и сверхзвуковой полет  Теодор фон карман, NASA Jet Propulsion Laboratory Родившийся в еврейской семье в Будапеште, фон Карман покинул Европу в 1930 году, чтобы занять должность в Калифорнийском технологическом институте. Он основал компанию Aerojet. В начале своей карьеры он создал примитивный вертолет. Карман как математик принял важное участие в разработке сверхзвукового полета, профиля крыла и сверхзвуковой аэродинамики, исследовании турбулентности. Во время Второй мировой войны фон Кармана давал консультации ВВС о потенциале немецких ракет. Он основал исследовательскую группу НАТО по вопросам воздухоплавания. Станислав Улам (Stanislaw Ulam), разработчик метода Монте-Карло  Станислав Улам, Los Alamos Laboratory Участник Манхэттенского проекта, польско-еврейский математик, имя которого стоит во второй половине принципа Теллера-Улама для термоядерного оружия. Кроме его работы в области ядерной физики, Улам также разработал метод моделирования, известный как метод Монте-Карло. Этот метод состоит в повторении сотен испытаний для оценки вероятности событий. Эта стратегия последовательно и повсеместно сегодня используется в моделировании. Источник: http://www.businessinsider.com/important-mathematicians-modern-world-2012-7?op=1 hijos.ru Проект "Великие математики древности". Всероссийский Конкурс исследовательских проектов, выполненных школьниками при научном консультировании Ученых Международной ассоциации строительных вузов Воронежский государственный технический университет Секция математики Номинация 10-11 классы Тема проекта: Великие математики древности Туголуков Денис Николаевич, (ученик 10 класса) [email protected] школа № 6, г.Калач Руководитель: учитель математики школы №6, г.Калач Приходченко Людмила Александровна Научный консультант: доцент кафедры высшей математики ВГТУ, к.ф.-м.н. Стенюхин Леонид Витальевич 2017 год Оглавление Титульный лист……………………………………………………. Аннотация работы………………………………………………….2 Сведения об авторе, руководителе и научном консультанте научной работы…………………..........3 Введение ……………………………………………………………4 Основная часть ……………………………………………………..6-11 Заключение…………………………………………………………12 Библиографический список……………………………………….13 АННОТАЦИЯ научной работы, представленной на Всероссийский Конкурс исследовательских проектов, выполненных школьниками при научном консультировании ученых Международной ассоциации строительных вузов 1.Название: Великие математики древности 2. Объем работы: с. 13 3.Количество иллюстраций: 2 ед. 4.Количество источников литературы: 6ед. Характеристика работы: Этот проект посвящен великим математикам древности, их жизни и достижениям… А так же изучению истории математики Древнего Египта. СВЕДЕНИЯ об авторе, руководителе и научном консультанте научной работы, представленной на Всероссийский Конкурс исследовательских проектов, выполненных школьниками и студентами при научном консультировании ученых Международной ассоциации строительных вузов АВТОР Фамилия Туголуков Имя Денис Отчество Николаевич Школа, класс МКОУ Калачеевская сош №6, 10 класс Телефон_________________________________________________
6. Адрес электронной почты [email protected] РУКОВОДИТЕЛЬ Фамилия Приходченко Имя Людмила Отчество Александровна Место работы г.Калач, сош №6 Должность учитель Ученая степень___________________________________________ Ученое звание____________________________________________ Телефон рабочий _________________________________________ Адрес электронной почты [email protected]
НАУЧНЫЙ КОНСУЛЬТАНТ Фамилия Стенюхин Имя Леонид Отчество Витальевич Место работы ВГТУ Должность преподаватель Ученая степень____________________________________________ Ученое звание доцент кафедры высшей математики ВГТУ Телефон рабочий __________________________________________ Адрес электронной почты [email protected]
ТВОРЧЕСКАЯ АКТИВНОСТЬ АВТОРА В ПРЕДШЕСТВУЮЩИЙ ПЕРИОД (участие автора работы в конкурсах и конференциях в текущем учебном году) Место проведения (город) Организатор мероприятия (вуз) Конференция Тема доклада Награды Научный консультант / Стенюхин Л.В / Руководитель / Приходченко Л.А / Автор работы / Туголуков Д.Н./ I .Введение Всегда интересно заглянуть в глубину веков, узнать о людях, которые умерли тысячи лет назад, попытаться понять их, почувствовать, чем они жили. Великие народы прошлого оставили нам бесценное наследие. Минули тысячелетия, но живой интерес к истории Древнего Египта не иссяк. Напротив! Только после дешифровки иероглифов перед нами обрисовалась во всём своём величии могучая цивилизация, процветавшая, уже пять тысяч лет тому назад на берегах Нила. Актуальность моей темы заключается в том, что изучая страницы истории, я убеждаюсь, что истоки появления математических идей, понятий, задач, связаны с практическими нуждами человека, поисками способов их преодоления. Они приобрели, современный вид благодаря теоретической мысли ученых разных столетий и народов. Время накопило коллекцию старинных задач, сохранивших особую популярность и сейчас. Задачи и теоремы, доказанные сотни лет назад, захватывают нас своей красотой, тонкостью логических рассуждений так же, как восхищались ими все предыдущие поколения. В них отражается весь сложный и извилистый труд, по которому развивалась математика. сведениями из истории становления и развития математики пробуждает у учеников интерес к науке, углубляет знания, формирует диалектико-философское мировоззрение, воспитывает патриотические чувства Изучая школьный курс «Истории древнего мира», меня заинтересовала эта тема. Мне захотелось расширить свои представления о Древнем Египте, а именно о развитии математики, о возникновении чисел, дробей. Любая наука, и математика в особенности, строится на фундаменте знаний, добытых в предшествующие эпохи. «Камни истории служат ступенями, ведущими в будущее»,- писал Н.К. Рерих. В своей работе я лишь чуть-чуть приоткрою завесу над прошлым, в котором еще столько тайн, столько увлекательного, столько неизведанного… Цель работы: Выработка навыков обобщения, систематизации, поиска закономерностей добывания информации. Задачи: 1. Изучить историю развития математики; 2.С помощью различных источников информаций: толковых словарей, научно-популярной литературы, художественной литературы, осмыслить роль вклада в науку древних учёных математиков; 3.Обобщить некоторые научные открытия в математике этих великих учёных и показать их роль в истории, в образовании. 4. Подбор материала о достижениях Архимеда 5. Подбор материала о жизни и достижениях Пифагора 6. Подбор материала о жизни и достижениях Р. Декарта 7. Подбор материала о жизни и достижениях С. В. Ковалевской Для подготовки своего проекта я использовал следующую литературу: Детская энциклопедия / Мифы и легенды народов мира, которая знакомит нас с мифами и легендами всех народов, в том числе Древнего Египта. Мы узнаем о богах, которым преклонялись древние люди, о священных ритуалах. Деревенский Б.Г. Книга «Древний Египет»,которая рассказывает о земле фараонов и пирамид, высоком искусстве и жестоких войнах. Дает яркое представление о том, как жили на берегах Нила в далекой древности от фараона Хуфу до царицы Нифертити, о том как тысячи лет назад возникла цивилизация, памятники и история которой по сей день изумляют нас. М. Матье «День египетского мальчика». Это историческая повесть посвященная мальчишкам, жившим более 30 веков тому назад в Древнем Египте, которые осваивают премудрости счета и письма в египетской школе. «Страна большого Хаппи». Эта книга об основах письменности и математического счета в Древнем Египте. Она знакомит нас с примерами и задачами, которые дошли до наших дней. Стройк Д.Я. «Краткий очерк истории математики». В очень скромном объеме автор дал последовательное изложение основных фактов, событий многовековой истории математики от ее зарождения до начала двадцатого столетия. Малых А.Е. «История математики к задачах». Здесь представлены задачи Древнего Египта и Вавилона, отражающие основные этапы и специфику развития математического знания.
II.Основная часть. 1. Мифы Древнего Египта Все народы с древних времен создавали мифы. Египтяне верили, что боги обитают повсюду. И на земле, где живут люди и в другом невидимом мире, куда люди отправляются после смерти. Египтяне поклонялись множеству богов, которые создали мир, охраняют его и заботятся о людях. В честь богов строили храмы и совершали жертвоприношение.(Приложение1) Вот некоторые из главных египетских богов: Ра, Осирис, Исида, Гор, Сет, Анубис, Хнум, Хатор, Хари, Себек, Птах и Тот. Тот бог мудрости и знаний. Он изобрел счет и писменность. Для счета времени и вообще для всякого счета он изобрел числа. И поэтому на древних рельефах его часто изображали с телом человека и головой священной птицы ибиса, чей шаг равнялся в точности одному кубиту, т.е. мере длины, которая применялась при строительстве священных сооружений. Основной мерой длины у древних египтян считался «локоть». Он был равен 52,3см. Локоть делится на 7 ладоней, ладонь – на 4 пальца, таким образом, локоть состоит из 28 пальцев. Встречались и большие меры длины, например, хет (жердь). Она состояла из 100 локтей, то есть 10,5 км. Мерой веса у древних египтян был «дебень», равный примерно 91 грамму. . [5], [6]. 2. Папирусы Математические папирусы «Наставление, как достигнуть знания всех темных(трудных, непонятных) вещей…всех тайн, которые скрывают в себе вещи…. Со старинных рукописей… писец Ахмес написал это» Сохранившаяся часть названия папируса Ринда. Египетская культура является одной из древних. Пирамиды, построенные много веков назад , храмы, памятники скульптуры. поражают своей строгостью и величием. Их возведение требовало огромной затраты труда, орудий производства и времени. Ясно, что без предварительных математических расчетов такое строительство не могло осуществиться. Таким образом, архитектура была важным стимулом развития арифметики и геометрии. Стены египетских храмов, гробниц и саркофагов покрыты загадочными знаками. Среди них можно разглядеть и змею кобру и птицу ибиса и пирамиду. Это так называемые иероглифы, в египетском письме их более 700. Их учились писать сначала на черепках битой посуды, а потом уже на папирусе, так как он был не дешёв. Этот материал, похожий на бумагу изготавливали так: стебель папируса разрезали на длинные узкие полоски, укладывали на гладкий стол в ряд. Сверху снова полоски в поперечном направлении. Всё это прижимали плоским камнем. Выделялся клейкий сок, который склеивал полосы, а после просушки получался готовый для письма лист, называемый «папирусом». Когда этот лист исписывали до конца, к нему подклеивали другой. Для хранения папирус сворачивали в трубочку – свиток. В одном музее хранится такой свиток, длиной более 40 метров. Наши познания о древнеегипетской математике основаны главным образом на двух больших папирусах математического характера и на нескольких небольших отрывках. Один из больших папирусов называется математическим папирусом Ринда (Rhind) Он примерно 5,5 м длины и 0,32 ширины. другой большой папирус называется Московским, почти такой же длины и 8 см ширины. Содержащиеся в них математические сведения относятся примерно к 2000 г. до н.э. Папирус Ринда представляет собой собрание 84 задач прикладного характера. При решении этих задач производятся действия с дробями, вычисляются площади прямоугольника, треугольника, трапеции и круга, объёмы параллелепипеда, цилиндра, размеры пирамид, имеются также задачи на пропорциональное деление, а при решении одной задачи находится сумма геометрической прогрессии. В московском папирусе собраны решения 25 задач. Большинство их такого же типа, как и в папирусе Ринда. Кроме того, в одной из задач правильно вычисляется объём усечённой пирамиды с квадратным основанием. В другой задаче содержится самый ранний в математике пример определения площади кривой поверхности: вычисляется боковая поверхность корзины, т.е. полуцилиндра, высота которого равна диаметру основания. Сохранились математические папирусы, в которых излагаются задачи и примеры, вычисления вместимости амбара, раздел имущества наследников и т. д. Встречаются в папирусах и задачи – шутки, рассчитанные на особых любителей математики. На основании математических папирусов учёные установили, что египетские математики решали уже уравнения с двумя неизвестными. Любопытно заметить, что нашему понятию х (икс) – неизвестное соответствовало египетское слово «куча». Имелось ввиду, очевидно, куча зерна, объём которой чаще всего приходилось высчитывать. 3. Древнеегипетские числа Факты убедительно свидетельствуют о том, что счет возникает раньше, чем названия чисел. Иначе говоря, первоначально языковыми объектами для построения модели служат не слова, а выделенные однотипные предметы: пальцы, камешки, узелки, черточки. Это и естественно. При возникновении языка слова связываются только с теми понятиями, которые уже существуют, т. е. распознаются. Чтобы передать численность какой-то группы предметов, человек пользуется стандартными предметами, устанавливая между ними — один за другим — взаимно однозначное соответствие. Это и есть счет. Когда счет становится распространенным и привычным делом, для наиболее часто встречающихся (т. е. небольших) групп стандартных предметов возникают и словесные обозначения. На некоторых числительных остались следы их происхождения. Так, русское слово «пять» подозрительно похоже на старославянское «пядь» — рука (пять пальцев). Чтобы передать большие числа, люди стали считать «большими единицами» — пятерками, десятками, двадцатками. Во всех известных нам системах счета большие единицы кратны пяти, что свидетельствует о том, что первым счетным инструментом всегда становились пальцы. Из комбинации больших единиц возникли еще большие единицы. В древнеегипетских папирусах встречаются отдельные иероглифы, изображающие числа до десяти миллионов. Иероглифы писали на камне, на обожженных глиняных табличках, на папирусе, пользуясь для письма тростниковыми перьями и особыми чернилами. Для цифр были свои значки, но не для всех. Египтяне не имели значков для нуля и для цифр от двух до девяти. Зато были значки для десяти, сотни, тысячи и т.д. Единицы они обозначали палочками, десятки знаком изображающим кусок веревки, сотни – свернутой веревкой, тысячи – болотным растением, десятки тысяч - пальцем, сотни тысяч – головастиком, а миллион – человеком, который даже руки поднял от удивления перед таким большим числом. Скажем для того, чтобы написать число 234, нужно было изобразить два значка 100, три значка 10 и четыре значка 1. Запись цифр внутри каждого из разрядов производилась простым увеличением количества знаков по принципу простейшего сложения. Например, число "1" передавалось одной чертой (I), "2"- , соответственно,- двумя (II), "3" - тремя (III)...."8" - восемью (IIIIIIII), "9" - девятью (IIIIIIIII) и т.д. Числа, содержащие несколько разрядов единиц, записывались по такому же принципу; при этом единицы высших разрядов выносились в начало записи. К примеру, запись числа 1.124.624 выглядела следующим образом: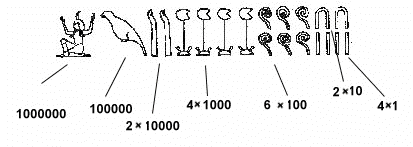 рис.1 рис.1 Следует отметить, что иероглиф рис. 2 имел значение "1.000.000" только в Древнем царстве. В последующие эпохи он переводится как "множество". рис. 2 имел значение "1.000.000" только в Древнем царстве. В последующие эпохи он переводится как "множество". Начало измерения, как и счета, относится к глубокой древности: мы находим его уже у первобытных народов. Измерение предполагает умение считать и требует дополнительно введения единицы измерения — меры измерительной процедуры, состоящей в сравнении измеряемого с единицей. Древнейшие меры связаны с человеческим телом: шаг, локоть, фут (ступня). С возникновением цивилизации потребность в счете и в умении выполнять арифметические действия резко увеличивается. При развитом общественном производстве регулирование отношений между людьми: обмен, раздел имущества, налогообложение — требует знания арифметики и элементов геометрии. И мы находим эти знания в древнейших из известных нам цивилизаций — вавилонской и египетской. Для обозначения чисел высших разрядов египтяне использовали запись умножения. Из четырех действий в математике египтяне знали только сложение и вычитание. Умножение было тем же сложением (таблица умножения не была известна), процесс сводился к постепенному удвоению числа. А деление сводилось к подысканию такого числа, на которое следовало умножить делитель, чтобы найти делимое. Например: 1.Сколько будет восемь раз по восемь 2. Взять 16 раз число 80 Умножение и деление сводилось к удвоению и сложению. Для их выполнения составились таблицы. Типичными для египетской математики являются задачи «на вместимость амбаров», «на хлеб и пиво» и др. Ряд задач сводится к вычислению суммы членов арифметической и геометрической прогрессии. Среди них знаменитая в истории математики задача – путешественница, которая в разных формулировках встречается у разных народов в различные эпохи. Например: 1.У семи людей по 7 кошек, каждая кошка съела 7 мышей, каждая мышь съела 7 колосков, каждый колос может дать 7 мер зерна. Найти сумму общего числа домов, кошек, мышей, колосьев и мер зерна? Ответ:21407. Проверка его показала, что эта задача решена правильно. . [3], [4]. 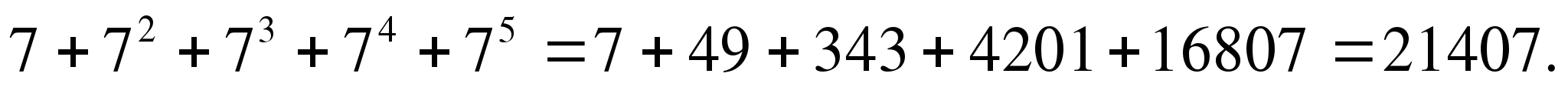 Сколько хлебов и сколько кувшинов пива можно получить с одной меры зерна, если из 15 мер получается 200 хлебов 10 кувшинов пива при условии, что выход пива составляет 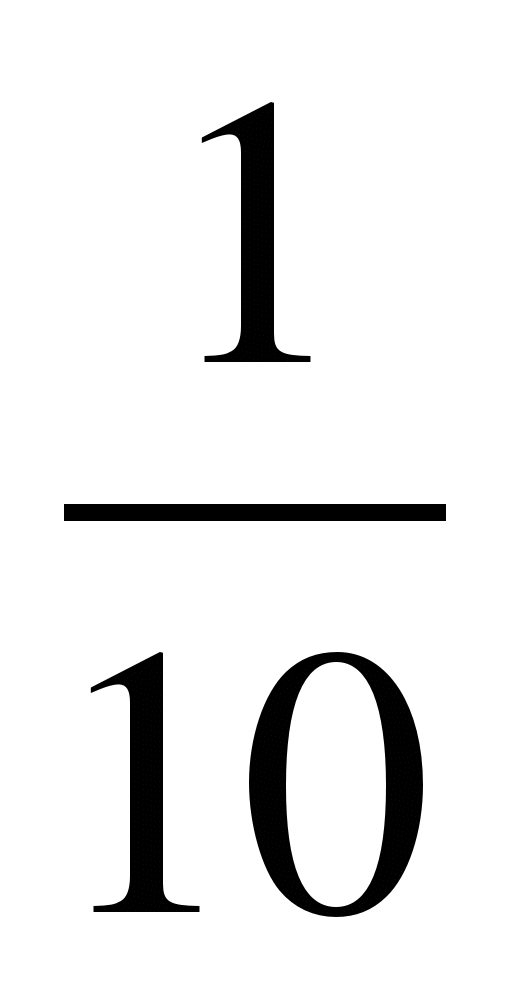 выхода хлеба! выхода хлеба!
Так как из 15 мер зерна получается 200 хлебов и 10 кувшинов пива, то из этого зерна выйдет только 30 кувшинов пива, а потому из одной меры выход пива составит 20 кувшина, тогда хлебов получиться 20. Строители великих египетских пирамид, храмов и дворцов должны были уметь точно вычислять площади треугольников, прямоугольников, многоугольников, объемы призм, пирамид; строить прямые углы, определять наклоны стены, крыши, ориентироваться по сторонам света. Наряду с точными приемами вычисления площадей у египтян имелись и приближенные, применявшиеся на практике, в землемерии. 4. Дроби Самой замечательной чертой египетской арифметики являются действия с дробями. Все дроби сводятся к суммам так называемых основных дробей, то есть дробей, имеющим числителем единицу. «Мудрость Тота была столь велика, что он придумал не только обычные целые числа, но и дроби. [1], [2]. Когда коварный Сет вырвал у спящего Хора глаз и разрезал его на 64 части, Тот нашел и срастил их, но 1/64 часть ему так и не удалось найти. С тех пор изображение части разрезанного глаза служила для всех египетских математиков обозначением дробей» Всякую дробь они представляли как одну часть какого – то числа. Поэтому у них всегда в числителе стояла 1, то есть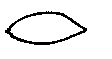 , а в знаменателе - нужное число. Например: , а в знаменателе - нужное число. Например: 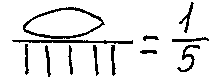 . . Чтобы выразить дробь, например: 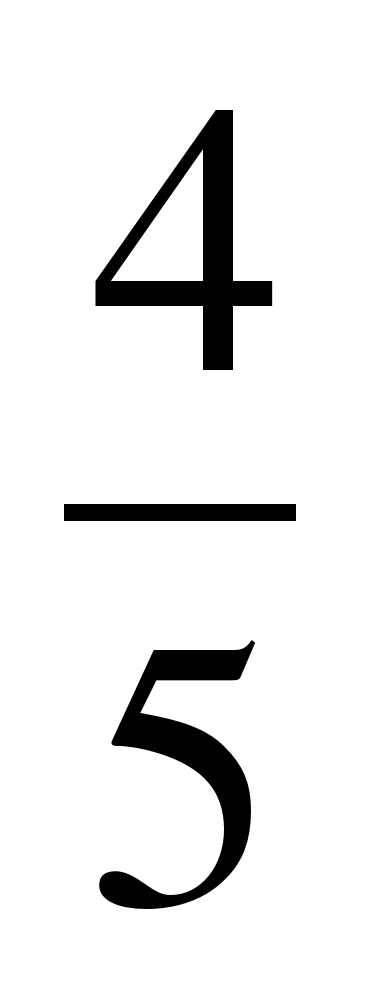 , они повторяли , они повторяли 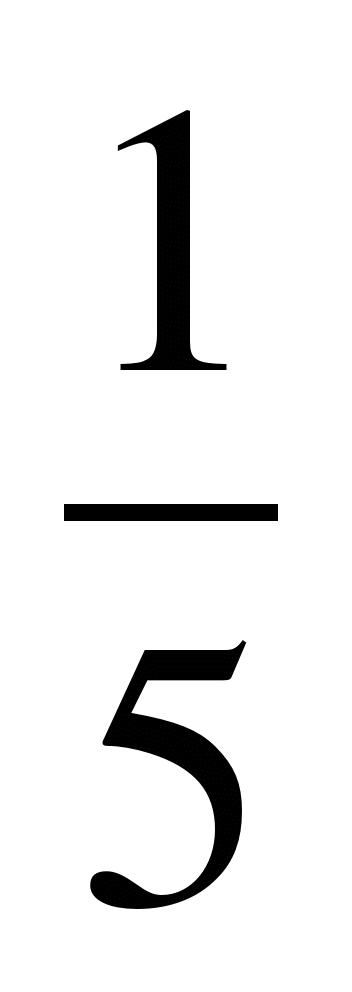 четыре раза. четыре раза.  Система дробей была громоздка и поэтому неудобна. Но как бы то ни было, египтяне знали дроби и широко пользовались ими в быту, выражая иногда очень мелкие дробные величины, например Система дробей была громоздка и поэтому неудобна. Но как бы то ни было, египтяне знали дроби и широко пользовались ими в быту, выражая иногда очень мелкие дробные величины, например 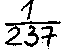 . Египтяне уже с древности знали, как поделить два яблока на троих. Для этого числа . Египтяне уже с древности знали, как поделить два яблока на троих. Для этого числа  у них был специальный значок у них был специальный значок  . Это была единственная дробь в обиходе египетских писцов, в которой в числителе не стояла единица. Для некоторых, часто употребляемых дробных чисел имелись особые знаки, например: . Это была единственная дробь в обиходе египетских писцов, в которой в числителе не стояла единица. Для некоторых, часто употребляемых дробных чисел имелись особые знаки, например:  . . Неосновные дроби записывались при помощи основных: 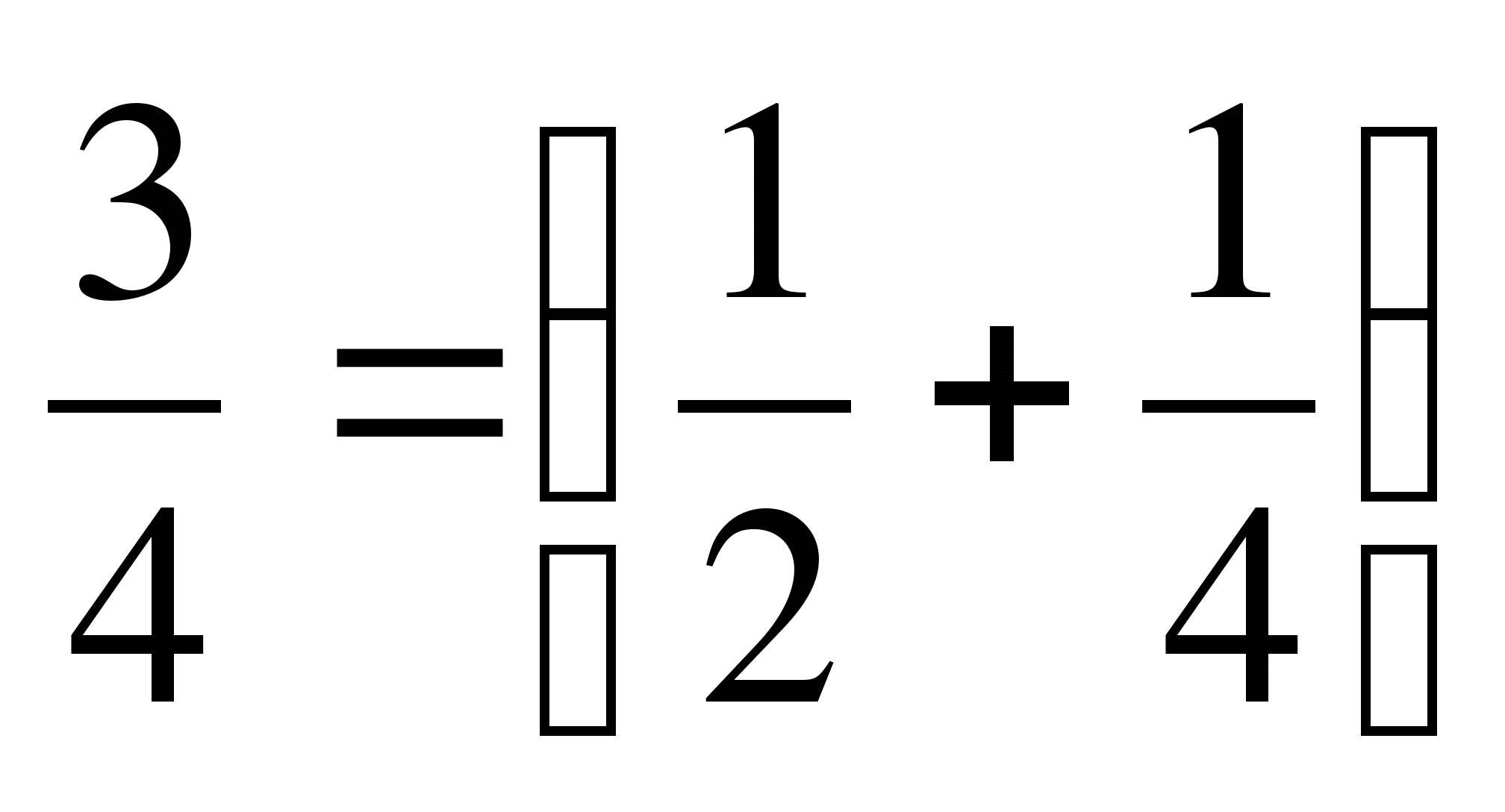  = = 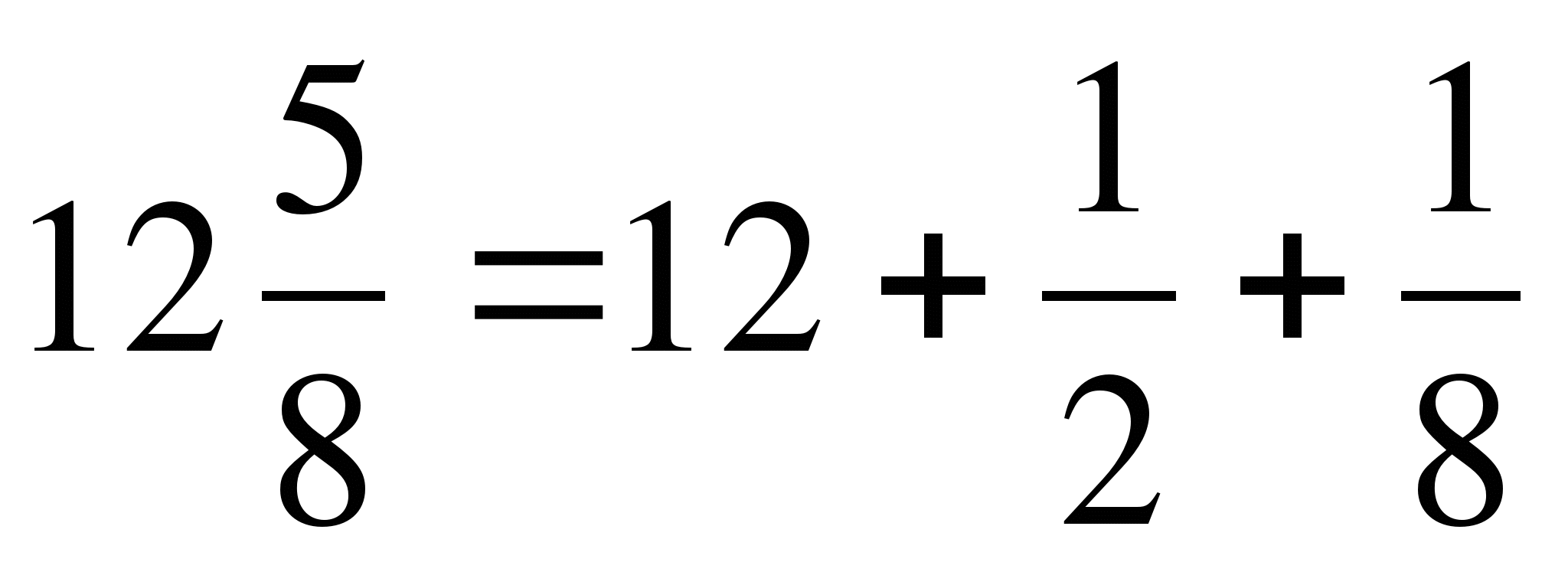 = = Сведение к суммам основных дробей производилось с помощью таблиц, которые давали разложение дробей вида 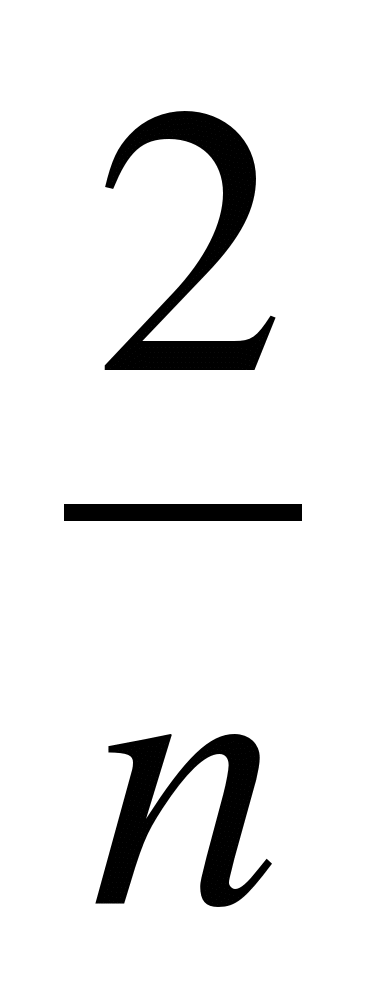 , так как умножение было двоичным. Папирус Ринда дает таблицу, в которой приведены разложения на основные дроби для всех нечетных п от 5 до 331, например , так как умножение было двоичным. Папирус Ринда дает таблицу, в которой приведены разложения на основные дроби для всех нечетных п от 5 до 331, например 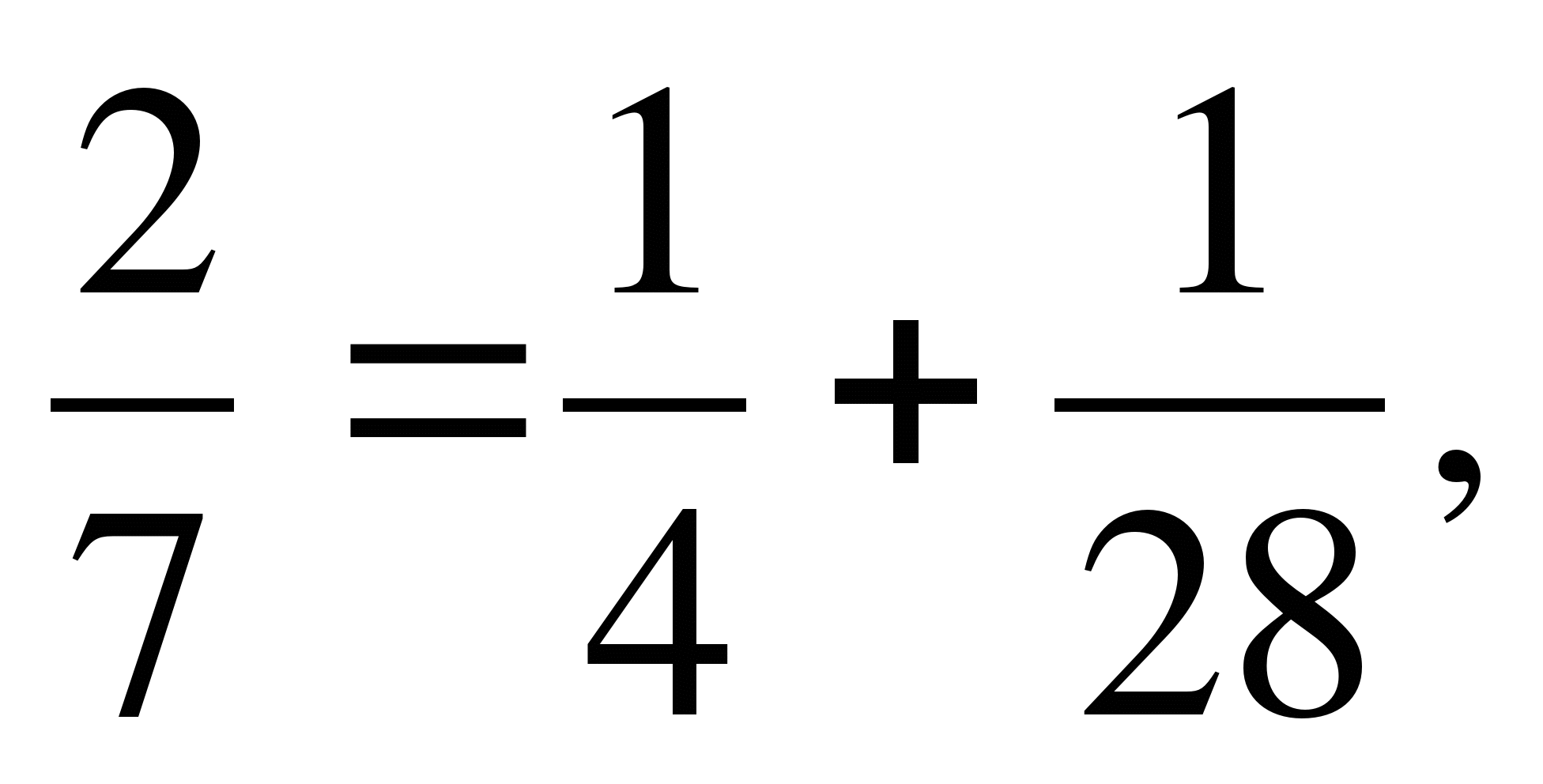 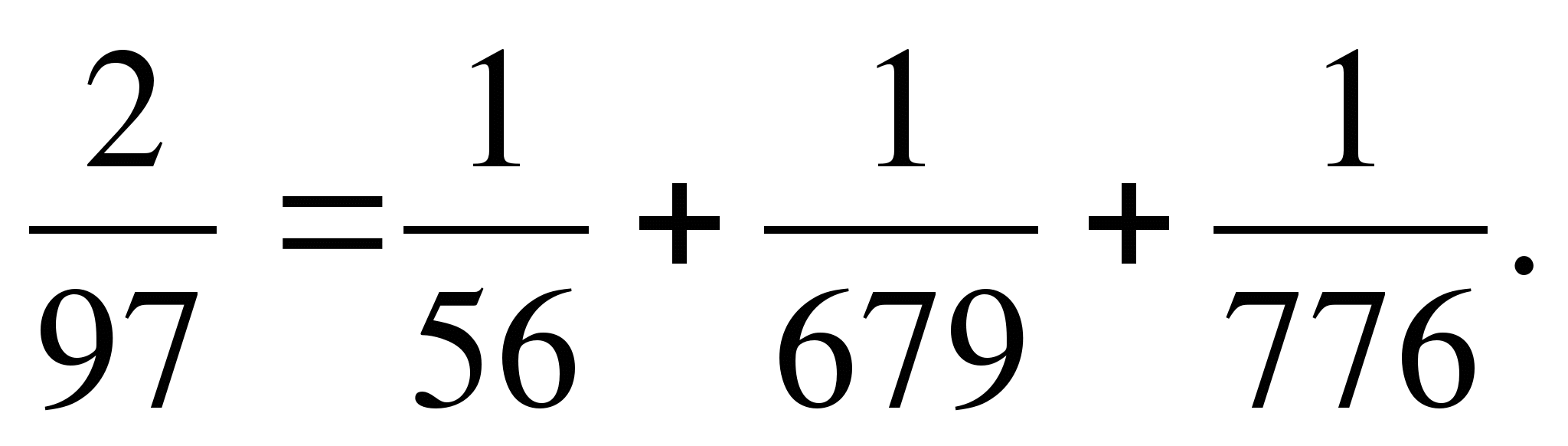 Из чего исходили при таком сведении к основным дробям , не ясно.(например, почему 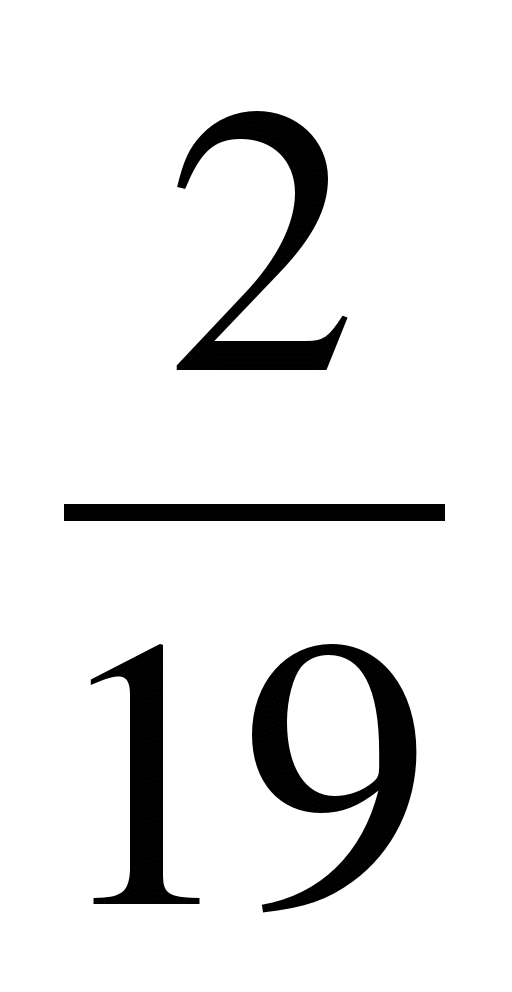 заменяется суммой заменяется суммой 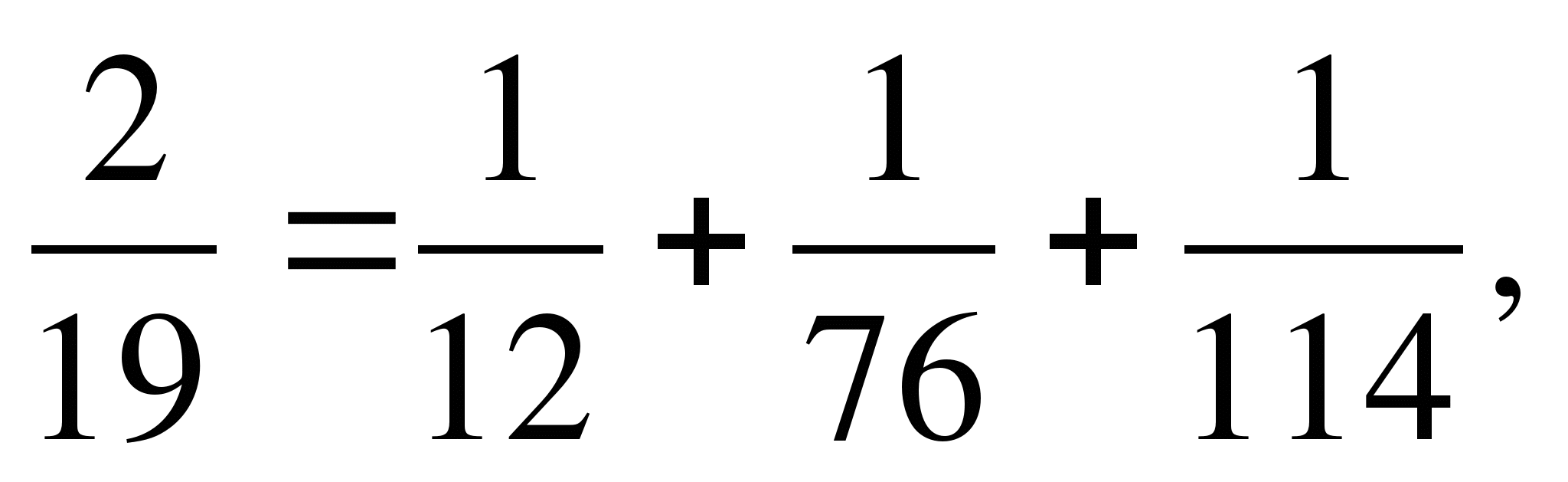 а не суммой а не суммой 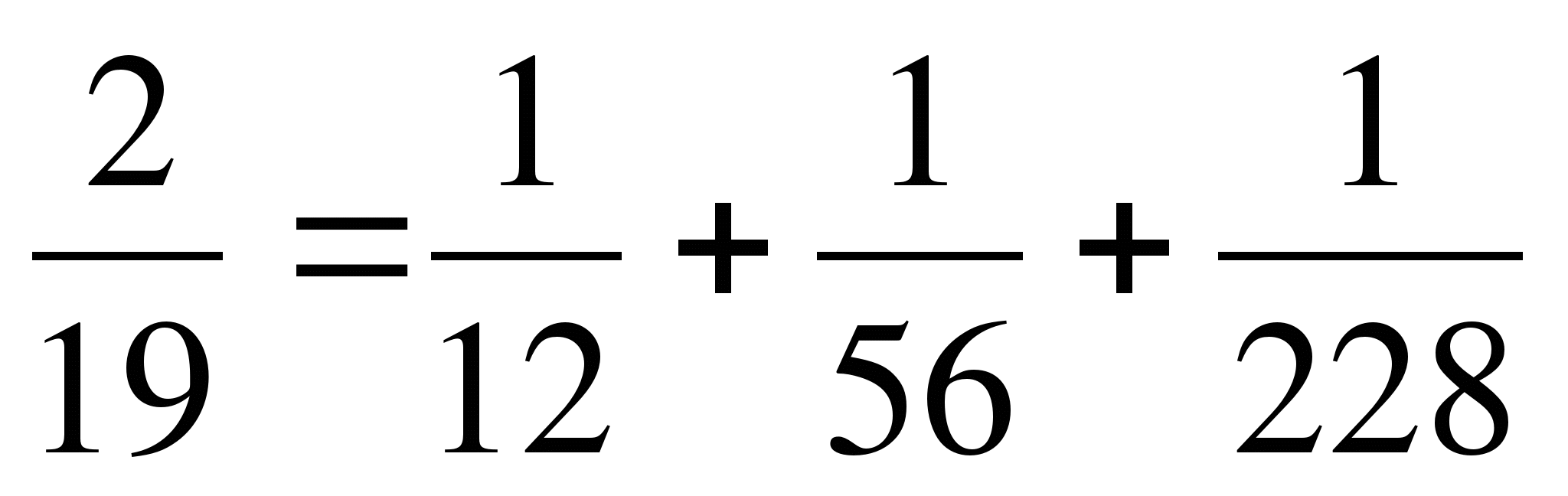 ?) ?) Такие действия с дробями придавали египетской математике тяжеловесность и растянутость. В то же время, указанное разложение предполагает определенное математическое искусство, и существуют интересные теории для объяснения того способа, каким египетские специалисты могли получить результаты. Многие задачи очень просты и сводятся к линейным уравнениям с одним неизвестным: Некое количество, его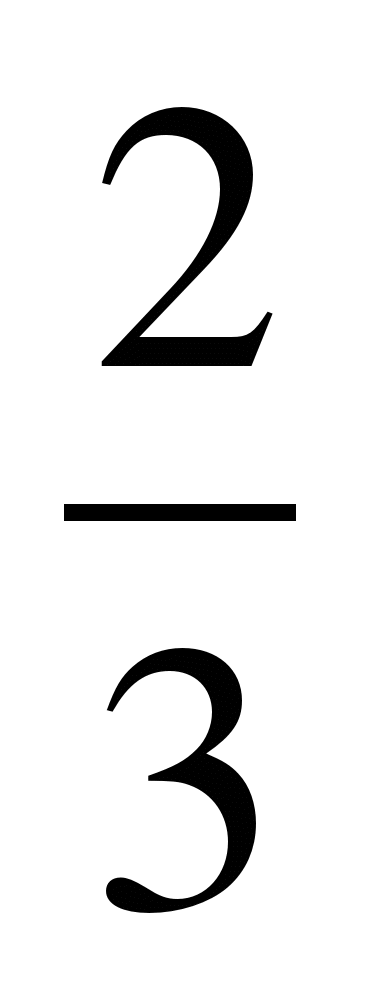 , его , его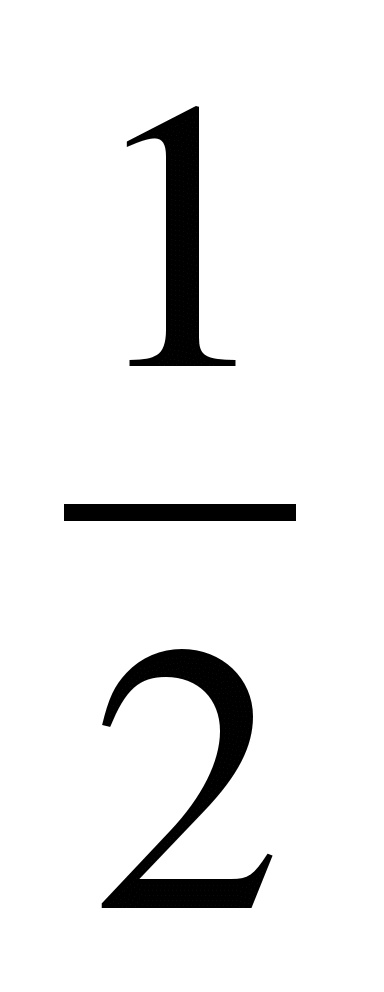 и его и его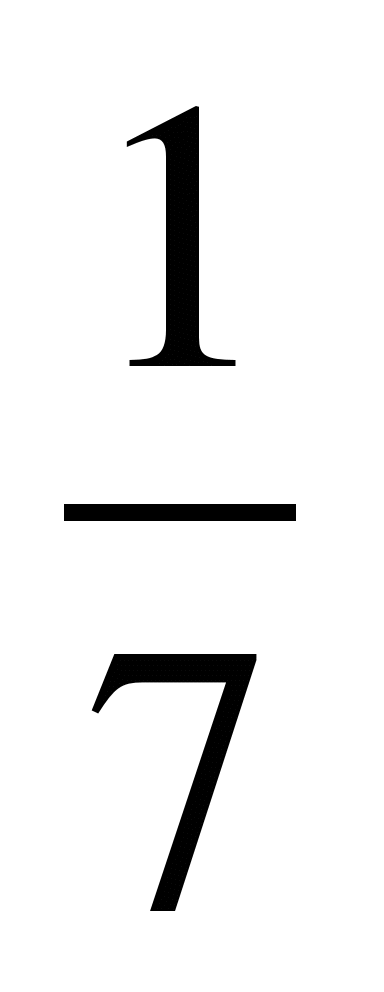 , сложенные вместе дают 33. Какое это количество? , сложенные вместе дают 33. Какое это количество? Ответ, 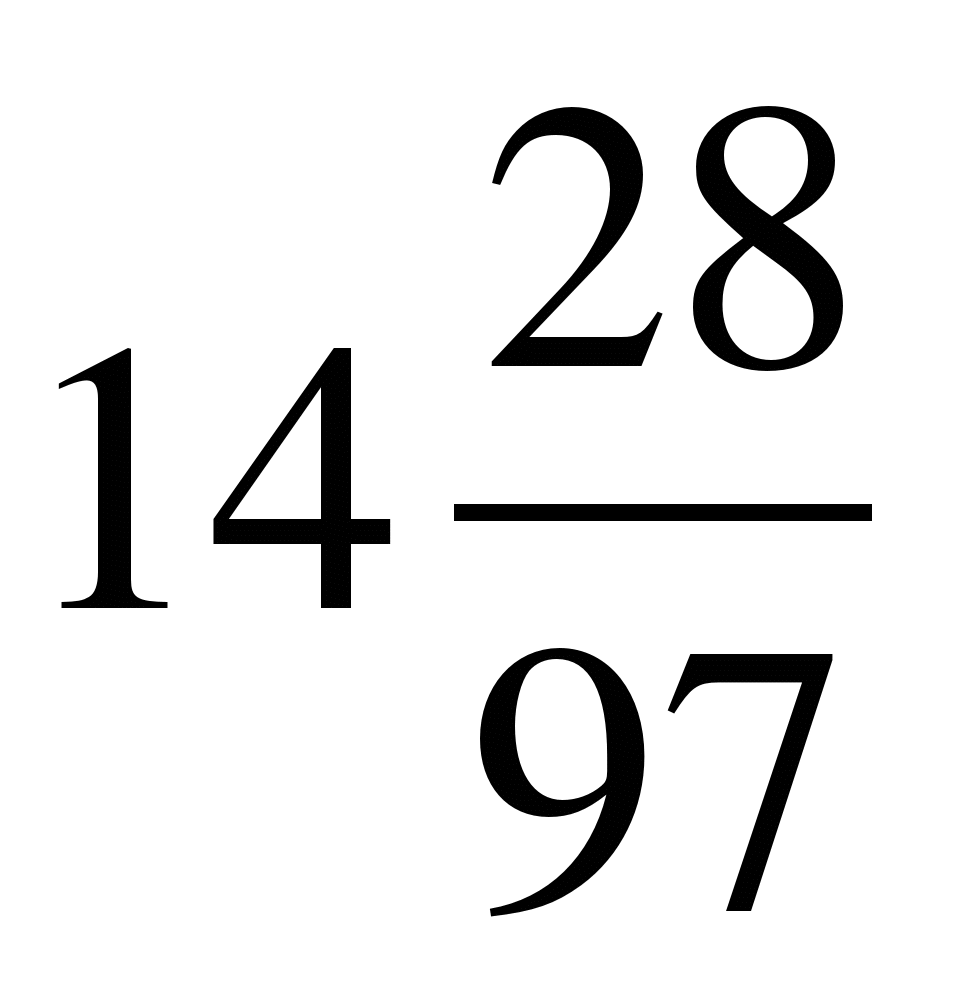 , записан в основных дробях: , записан в основных дробях: 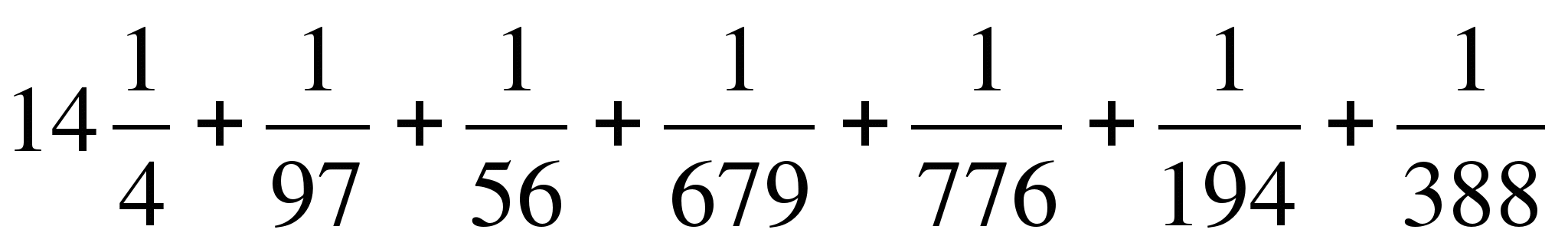 . Для неизвестного в уравнении существовал иероглиф, обозначавший «кучу» и произносились «хау» и «аха». Поэтому египетскую математику иногда называли «хау- исчислением». . [1], [2]. . Для неизвестного в уравнении существовал иероглиф, обозначавший «кучу» и произносились «хау» и «аха». Поэтому египетскую математику иногда называли «хау- исчислением». . [1], [2]. III. Заключение Самые ранние математические задачи, решения которых требовала повседневная жизнь, появились в Древнем Египте. Ведь без расчетов невозможно построить здание, будь то дворец или просто склад для зерна; поделить землю между родственниками, прибыль между торговцами и т.д. Выполняя данную работу, я старался вообразить себе египетских великих математиков, но из-за скудности источников мне это не удалось. Можно себе представить известных греческих ученых как Пифагор, Архимед, Эратосфен. Что же касается египетских и вавилонских математиков, то мы не знаем их даже имен. Зачем нужна история математики? Каждый знает, что мы живем в эпоху техники, но очень редко отдает себе отчет о том, что буквально вся наша техника основана на математике и физике. Когда вечером мы возвращаемся на автобусе домой, зажигаем электрический свет и включаем радио, то все это действует при помощи искусственных физических приспособлений, в основе которых лежат математические расчеты. Материалы, содержащиеся в папирусах, позволяют утверждать, что за 20 веков до нашей эры в Египте начали складываться элементы математики как науки. Эти элементы ещё только начинают выделяться из практических задач, целиком подчинены их содержанию. Техника вычислений ещё примитивна, методы решения задач не единообразны. Однако материалов, которые позволяли бы судить о развитии математики в Египте, ещё недостаточно. Единичная система счисления первобытных людей рисовавших палочки на стенах пещеры или зарубки на деревьях не забыты и в наши дни. Например: как узнать на каком курсе учится курсант военного училища? Для этого стоит только сосчитать, сколько полосок нашито на рукаве его мундира. О количестве самолетов противника сбитых ассом в воздушных боях говорит число звездочек нарисованных на фюзеляже его самолета. Мой интерес к истории Древнего Египта на этом не заканчивается. Хотелось бы как можно больше узнать о талантливом и трудолюбивом народе Древнего Египта, о его достижениях не только в области науки математики, но и других не менее точных наук Моя гипотеза о том, что изучая историю развития математики, человек понимает, что любая наука, и математика в особенности, строится на фундаменте знаний, добытых в предшествующие эпохи. В ходе подготовки к данному проекту я приобрёл много новых знаний, которые я буду использовать в своём образовании. IV. Библиографический список: 1. Детская энциклопедия / Мифы и легенды народов мира, которая знакомит нас с мифами и легендами всех народов, в том числе Древнего Египта. Мы узнаем о богах, которым преклонялись древние люди, о священных ритуалах. 2.Деревенский Б.Г. Книга «Древний Египет»,которая рассказывает о земле фараонов и пирамид, высоком искусстве и жестоких войнах. Дает яркое представление о том, как жили на берегах Нила в далекой древности от фараона Хуфу до царицы Нифертити, о том как тысячи лет назад возникла цивилизация, памятники и история которой по сей день изумляют нас. 3.М. Матье «День египетского мальчика». Это историческая повесть посвященная мальчишкам, жившим более 30 веков тому назад в Древнем Египте, которые осваивают премудрости счета и письма в египетской школе. 4. «Страна большого Хаппи». Эта книга об основах письменности и математического счета в Древнем Египте. Она знакомит нас с примерами и задачами, которые дошли до наших дней. 5.Стройк Д.Я. «Краткий очерк истории математики». В очень скромном объеме автор дал последовательное изложение основных фактов, событий многовековой истории математики от ее зарождения до начала двадцатого столетия. 6.Малых А.Е. «История математики к задачах». Здесь представлены задачи Древнего Египта и Вавилона, отражающие основные этапы и специфику развития математического знания. infourok.ru Математика в древности.Египет. Наше
знание древнеегипетской математики
основано главным образом на двух
папирусах, датируемых примерно 1700 до н.э.
Излагаемые в этих папирусах
математические сведения восходят к еще
более раннему периоду – ок. 3500 до н.э.
Египтяне использовали математику,
чтобы вычислять вес тел, площади
посевов и объемы зернохранилищ,
размеры податей и количество камней,
требуемое для возведения тех или иных
сооружений. В папирусах можно найти
также задачи, связанные с определением
количества зерна, необходимого для
приготовления заданного числа кружек
пива, а также более сложные задачи,
связанные с различием в сортах зерна;
для этих случаев вычислялись
переводные коэффициенты.
Но главной областью
применения математики была астрономия,
точнее расчеты, связанные с календарем.
Календарь использовался для
определения дат религиозных
праздников и предсказания ежегодных
разливов Нила. Однако уровень развития
астрономии в Древнем Египте намного
уступал уровню ее развития в Вавилоне.
Древнеегипетская
письменность основывалась на
иероглифах. Система счисления того
периода также уступала вавилонской.
Египтяне пользовались непозиционной
десятичной системой, в которой числа от
1 до 9 обозначались соответствующим
числом вертикальных черточек, а для
последовательных степеней числа 10
вводились индивидуальные символы.
Последовательно комбинируя эти
символы, можно было записать любое
число. С появлением папируса возникло
так называемое иератическое письмо-скоропись,
способствовавшее, в свою очередь,
появлению новой числовой системы. Для
каждого из чисел от 1 до 9 и для каждого
из первых девяти кратных чисел 10, 100 и т.д.
использовался специальный
опознавательный символ. Дроби
записывались в виде суммы дробей с
числителем, равным единице. С такими
дробями египтяне производили все
четыре арифметические операции, но
процедура таких вычислений оставалась
очень громоздкой.
Геометрия у египтян
сводилась к вычислениям площадей
прямоугольников, треугольников,
трапеций, круга, а также формулам
вычисления объемов некоторых тел. Надо
сказать, что математика, которую
египтяне использовали при
строительстве пирамид, была простой и
примитивной.
Задачи и решения,
приведенные в папирусах,
сформулированы чисто рецептурно, без
каких бы то ни было объяснений.
Египтяне имели дело только с
простейшими типами квадратных
уравнений и арифметической и
геометрической прогрессиями, а потому
и те общие правила, которые они смогли
вывести, были также самого простейшего
вида. Ни вавилонская, ни египетская
математики не располагали общими
методами; весь свод математических
знаний представлял собой скопление
эмпирических формул и правил.
Хотя майя, жившие в
Центральной Америке, не оказали
влияния на развитие математики, их
достижения, относящиеся примерно к 4 в.,
заслуживают внимания. Майя, по-видимому,
первыми использовали специальный
символ для обозначения нуля в своей
двадцатиричной системе. У них были две
системы счисления: в одной применялись
иероглифы, а в другой, более
распространенной, точка обозначала
единицу, горизонтальная черта – число
5, а символ  обозначал нуль. Позиционные
обозначения начинались с числа 20, а
числа записывались по вертикали сверху
вниз..
обозначал нуль. Позиционные
обозначения начинались с числа 20, а
числа записывались по вертикали сверху
вниз..
Классическая
Греция. С точки зрения 20 в.
родоначальниками математики явились
греки классического периода (6–4 вв. до н.э.).
Математика, существовавшая в более
ранний период, была набором
эмпирических заключений. Напротив, в
дедуктивном рассуждении новое
утверждение выводится из принятых
посылок способом, исключавшим
возможность его неприятия.
Настаивание греков на
дедуктивном доказательстве было
экстраординарным шагом. Ни одна другая
цивилизация не дошла до идеи получения
заключений исключительно на основе
дедуктивного рассуждения, исходящего из
явно сформулированных аксиом. Одно из
объяснений приверженности греков
методам дедукции мы находим в
устройстве греческого общества
классического периода. Математики и
философы (нередко это были одни и те же
лица) принадлежали к высшим слоям
общества, где любая практическая
деятельность рассматривалась как
недостойное занятие. Математики
предпочитали абстрактные рассуждения о
числах и пространственных отношениях
решению практических задач. Математика
делилась на арифметику – теоретический
аспект и логистику – вычислительный
аспект. Заниматься логистикой
предоставляли свободнорожденным низших
классов и рабам.
Греческая система
счисления была основана на
использовании букв алфавита. Аттическая
система, бывшая в ходу с 6–3 вв. до н.э.,
использовала для обозначения единицы
вертикальную черту, а для обозначения
чисел 5, 10, 100, 1000 и 10 000 начальные буквы их
греческих названий. В более поздней
ионической системе счисления для
обозначения чисел использовались 24
буквы греческого алфавита и три
архаические буквы. Кратные 1000 до 9000
обозначались так же, как первые девять
целых чисел от 1 до 9, но перед каждой
буквой ставилась вертикальная черта.
Десятки тысяч обозначались буквой М (от
греческого мириои – 10 000), после которой
ставилось то число, на которое нужно
было умножить десять тысяч.
Дедуктивный характер
греческой математики полностью
сформировался ко времени Платона и
Аристотеля. Изобретение дедуктивной
математики принято приписывать Фалесу
Милетскому (ок. 640–546 до н.э.), который, как
и многие древнегреческие математики
классического периода, был также
философом. Высказывалось предположение,
что Фалес использовал дедукцию для
доказательства некоторых результатов в
геометрии, хотя это сомнительно.
Другим великим греком, с
чьим именем связывают развитие
математики, был Пифагор (ок. 585–500 до н.э.).
Полагают, что он мог познакомиться с
вавилонской и египетской математикой во
время своих долгих странствий. Пифагор
основал движение, расцвет которого
приходится на период ок. 550–300 до н.э.
Пифагорейцы создали чистую математику в
форме теории чисел и геометрии. Целые
числа они представляли в виде
конфигураций из точек или камешков,
классифицируя эти числа в соответствии
с формой возникающих фигур («фигурные
числа»). Слово «калькуляция» (расчет,
вычисление) берет начало от греческого
слова, означающего «камешек». Числа 3, 6, 10
и т.д. пифагорейцы называли треугольными,
так как соответствующее число камешков
можно расположить в виде треугольника,
числа 4, 9, 16 и т.д. – квадратными, так как
соответствующее число камешков можно
расположить в виде квадрата, и т.д.
Из простых геометрических
конфигураций возникали некоторые
свойства целых чисел. Например,
пифагорейцы обнаружили, что сумма двух
последовательных треугольных чисел
всегда равна некоторому квадратному
числу. Они открыли, что если (в
современных обозначениях) n2 –
квадратное число, то n2 + 2n +1 = (n + 1)2.
Число, равное сумме всех своих
собственных делителей, кроме самого
этого числа, пифагорейцы называли
совершенным. Примерами совершенных
чисел могут служить такие целые числа,
как 6, 28 и 496. Два числа пифагорейцы
называли дружественными, если каждое из
чисел равно сумме делителей другого;
например, 220 и 284 – дружественные числа (и
здесь само число исключается из
собственных делителей).
Для пифагорейцев любое
число представляло собой нечто большее,
чем количественную величину. Например,
число 2 согласно их воззрению означало
различие и потому отождествлялось с
мнением. Четверка представляла
справедливость, так как это первое число,
равное произведению двух одинаковых
множителей.
Пифагорейцы также открыли,
что сумма некоторых пар квадратных
чисел есть снова квадратное число.
Например, сумма 9 и 16 равна 25, а сумма 25 и
144 равна 169. Такие тройки чисел, как 3, 4 и 5
или 5, 12 и 13, называются пифагоровыми
числами. Они имеют геометрическую
интерпретацию, если два числа из тройки
приравнять длинам катетов
прямоугольного треугольника, то третье
число будет равно длине его гипотенузы.
Такая интерпретация, по-видимому,
привела пифагорейцев к осознанию более
общего факта, известного ныне под
названием теоремы Пифагора, согласно
которой в любом прямоугольном
треугольнике квадрат длины гипотенузы
равен сумме квадратов длин катетов.
Рассматривая прямоугольный
треугольник с единичными катетами,
пифагорейцы обнаружили, что длина его
гипотенузы равна  ,
и это повергло их в смятение, ибо они
тщетно пытались представить число ,
и это повергло их в смятение, ибо они
тщетно пытались представить число  в
виде отношения двух целых чисел, что
было крайне важно для их философии.
Величины, непредставимые в виде
отношения целых чисел, пифагорейцы
назвали несоизмеримыми; современный
термин – «иррациональные числа». Около
300 до н.э. Евклид доказал, что число в
виде отношения двух целых чисел, что
было крайне важно для их философии.
Величины, непредставимые в виде
отношения целых чисел, пифагорейцы
назвали несоизмеримыми; современный
термин – «иррациональные числа». Около
300 до н.э. Евклид доказал, что число  несоизмеримо.
Пифагорейцы имели дело с
иррациональными числами, представляя
все величины геометрическими образами.
Если 1 и несоизмеримо.
Пифагорейцы имели дело с
иррациональными числами, представляя
все величины геометрическими образами.
Если 1 и  считать
длинами некоторых отрезков, то различие
между рациональными и иррациональными
числами сглаживается. Произведение
чисел считать
длинами некоторых отрезков, то различие
между рациональными и иррациональными
числами сглаживается. Произведение
чисел  и и  есть
площадь прямоугольника со сторонами
длиной есть
площадь прямоугольника со сторонами
длиной  и и  .Мы
и сегодня иногда говорим о числе 25 как о
квадрате 5, а о числе 27 – как о кубе 3. .Мы
и сегодня иногда говорим о числе 25 как о
квадрате 5, а о числе 27 – как о кубе 3.
Древние греки решали
уравнения с неизвестными посредством
геометрических построений. Были
разработаны специальные построения для
выполнения сложения, вычитания,
умножения и деления отрезков,
извлечения квадратных корней из длин
отрезков; ныне этот метод называется
геометрической алгеброй.
Приведение задач к
геометрическому виду имело ряд важных
последствий. В частности, числа стали
рассматриваться отдельно от геометрии,
поскольку работать с несоизмеримыми
отношениями можно было только с помощью
геометрических методов. Геометрия стала
основой почти всей строгой математики
по крайней мере до1600. И даже в 18 в., когда
уже были достаточно развиты алгебра и
математический анализ, строгая
математика трактовалась как геометрия,
и слово «геометр» было равнозначно
слову «математик».
Именно пифагорейцам мы во
многом обязаны той математикой, которая
затем была систематизированно изложена
и доказана в Началах Евклида. Есть
основания полагать, что именно они
открыли то, что ныне известно как
теоремы о треугольниках, параллельных
прямых, многоугольниках, окружностях,
сферах и правильных многогранниках.
Одним из самых выдающихся
пифагорейцев был Платон (ок. 427–347 до н.э.).
Платон был убежден, что физический мир
постижим лишь посредством математики.
Считается, что именно ему принадлежит
заслуга изобретения аналитического
метода доказательства. (Аналитический
метод начинается с утверждения, которое
требуется доказать, и затем из него
последовательно выводятся следствия до
тех пор, пока не будет достигнут какой-нибудь
известный факт; доказательство
получается с помощью обратной процедуры.)
Принято считать, что последователи
Платона изобрели метод доказательства,
получивший название «доказательство от
противного». Заметное место в истории
математики занимает Аристотель, ученик
Платона. Аристотель заложил основы
науки логики и высказал ряд идей
относительно определений, аксиом,
бесконечности и возможности
геометрических построений.
Величайшим из греческих
математиков классического периода,
уступавшим по значимости полученных
результатов только Архимеду, был Евдокс
(ок. 408–355 до н.э.). Именно он ввел понятие
величины для таких объектов, как отрезки
прямых и углы. Располагая понятием
величины, Евдокс логически строго
обосновал пифагорейский метод
обращения с иррациональными числами.
Работы Евдокса позволили
установить дедуктивную структуру
математики на основе явно формулируемых
аксиом. Ему же принадлежит и первый шаг в
создании математического анализа,
поскольку именно он изобрел метод
вычисления площадей и объемов,
получивший название «метода
исчерпывания». Этот метод состоит в
построении вписанных и описанных
плоских фигур или пространственных тел,
которые заполняют («исчерпывают»)
площадь или объем той фигуры или того
тела, которое является предметом
исследования. Евдоксу же принадлежит и
первая астрономическая теория,
объясняющая наблюдаемое движение
планет. Предложенная Евдоксом теория
была чисто математической; она
показывала, каким образом комбинации
вращающихся сфер с различными радиусами
и осями вращения могут объяснить
кажущиеся нерегулярными движения
Солнца, Луны и планет.
Около 300 до н.э. результаты
многих греческих математиков были
сведены в единое целое Евклидом,
написавшим математический шедевр
Начала. Из немногих проницательно
отобранных аксиом Евклид вывел около 500
теорем, охвативших все наиболее важные
результаты классического периода. Свое
сочинение Евклид начал с определения
таких терминов, как прямая, угол и
окружность. Затем он сформулировал
десять самоочевидных истин, таких, как «целое
больше любой из частей». И из этих десяти
аксиом Евклид смог вывести все теоремы.
Для математиков текст Начал Евклида
долгое время служил образцом строгости,
пока в 19 в. не обнаружилось, что в нем
имеются серьезные недостатки, такие как
неосознанное использование
несформулированных в явном виде
допущений.
Аполлоний (ок. 262–200 до н.э.)
жил в александрийский период, но его
основной труд выдержан в духе
классических традиций. Предложенный им
анализ конических сечений – окружности,
эллипса, параболы и гиперболы – явился
кульминацией развития греческой
геометрии. Аполлоний также стал
основателем количественной
математической астрономии.
Александрийский
период. В этот период, который
начался около 300 до н.э., характер
греческой математики изменился.
Александрийская математика возникла в
результате слияния классической
греческой математики с математикой
Вавилонии и Египта. В целом математики
александрийского периода были больше
склонны к решению чисто технических
задач, чем к философии. Великие
александрийские математики – Эратосфен,
Архимед, Гиппарх, Птолемей, Диофант и
Папп – продемонстрировали силу
греческого гения в теоретическом
абстрагировании, но столь же охотно
применяли свой талант к решению
практических проблем и чисто
количественных задач.
Эратосфен (ок. 275–194 до н.э.)
нашел простой метод точного вычисления
длины окружности Земли, ему же
принадлежит календарь, в котором каждый
четвертый год имеет на один день больше,
чем другие. Астроном Аристарх (ок. 310–230
до н.э.) написал сочинение О размерах и
расстояниях Солнца и Луны, содержавшее
одну из первых попыток определения этих
размеров и расстояний; по своему
характеру работа Аристарха была
геометрической.
Величайшим математиком
древности был Архимед (ок. 287–212 до н.э.).
Ему принадлежат формулировки многих
теорем о площадях и объемах сложных
фигур и тел, вполне строго доказанные им
методом исчерпывания. Архимед всегда
стремился получить точные решения и
находил верхние и нижние оценки для
иррациональных чисел. Например, работая
с правильным 96-угольником, он
безукоризненно доказал, что точное
значение числа p находится между 31/7
и 310/71. Архимед доказал также
несколько теорем, содержавших новые
результаты геометрической алгебры. Ему
принадлежит формулировка задачи о
рассечении шара плоскостью так, чтобы
объемы сегментов находились между собой
в заданном отношении. Архимед решил эту
задачу, отыскав пересечение параболы и
равнобочной гиперболы.
Архимед был величайшим
математическим физиком древности. Для
доказательства теорем механики он
использовал геометрические соображения.
Его сочинение О плавающих телах
заложило основы гидростатики. Согласно
легенде, Архимед открыл носящий его имя
закон, согласно которому на тело,
погруженное в воду, действует
выталкивающая сила, равная весу
вытесненной им жидкости, во время
купания, находясь в ванной, и не в силах
совладать с охватившей его радостью
открытия, выбежал обнаженный на улицу с
криком: «Эврика!» («Открыл!»)
Во времена Архимеда уже не
ограничивались геометрическими
построениями, осуществимыми только с
помощью циркуля и линейки. Архимед
использовал в своих построениях спираль,
а Диоклес (конец 2 в. до н.э.) решил
проблему удвоения куба с помощью
введенной им кривой, получившей
название циссоиды.
В александрийский период
арифметика и алгебра рассматривались
независимо от геометрии. Греки
классического периода имели логически
обоснованную теорию целых чисел, однако
александрийские греки, восприняв
вавилонскую и египетскую арифметику и
алгебру, во многом утратили уже
наработанные представления о
математической строгости. Живший между
100 до н.э. и 100 н.э. Герон Александрийский
трансформировал значительную часть
геометрической алгебры греков в
откровенно нестрогие вычислительные
процедуры. Однако, доказывая новые
теоремы евклидовой геометрии, он по-прежнему
руководствовался стандартами
логической строгости классического
периода.
Первой достаточно
объемистой книгой, в которой арифметика
излагалась независимо от геометрии,
было Введение в арифметику Никомаха (ок.
100 н.э.). В истории арифметики ее роль
сравнима с ролью Начал Евклида в истории
геометрии. На протяжении более 1000 лет
она служила стандартным учебником,
поскольку в ней ясно, четко и
всеобъемлюще излагалось учение о целых
числах (простых, составных, взаимно
простых, а также о пропорциях). Повторяя
многие пифагорейские утверждения,
Введение Никомаха вместе с тем шло
дальше, так как Никомах видел и более
общие отношения, хотя и приводил их без
доказательства.
Знаменательной вехой в
алгебре александрийских греков стали
работы Диофанта (ок. 250). Одно из главных
его достижений связано с введением в
алгебру начал символики. В своих работах
Диофант не предлагал общих методов, он
имел дело с конкретными положительными
рациональными числами, а не с их
буквенными обозначениями. Он заложил
основы т.н. диофантова анализа –
исследования неопределенных уравнений.
Высшим достижением
александрийских математиков стало
создание количественной астрономии.
Гиппарху (ок. 161–126 до н.э.) мы обязаны
изобретением тригонометрии. Его метод
был основан на теореме, утверждающей,
что в подобных треугольниках отношение
длин любых двух сторон одного из них
равно отношению длин двух
соответственных сторон другого. В
частности, отношение длины катета,
лежащего против острого угла А в
прямоугольном треугольнике, к длине
гипотенузы должно быть одним и тем же
для всех прямоугольных треугольников,
имеющих один и тот же острый угол А. Это
отношение известно как синус угла А.
Отношения длин других сторон
прямоугольного треугольника получили
название косинуса и тангенса угла А.
Гиппарх изобрел метод вычисления таких
отношений и составил их таблицы.
Располагая этими таблицами и легко
измеримыми расстояниями на поверхности
Земли, он смог вычислить длину ее
большой окружности и расстояние до Луны.
По его расчетам, радиус Луны составил
одну треть земного радиуса; по
современным данным отношение радиусов
Луны и Земли составляет 27/1000. Гиппарх
определил продолжительность солнечного
года с ошибкой всего лишь в 61/2
минуты; считается, что именно он ввел
широты и долготы.
Греческая тригонометрия и
ее приложения в астрономии достигли
пика своего развития в Альмагесте
египтянина Клавдия Птолемея (умер в 168 н.э.).
В Альмагесте была представлена теория
движения небесных тел, господствовавшая
вплоть до 16 в., когда ее сменила теория
Коперника. Птолемей стремился построить
самую простую математическую модель,
сознавая, что его теория – всего лишь
удобное математическое описание
астрономических явлений, согласованное
с наблюдениями. Теория Коперника
одержала верх именно потому, что как
модель она оказалась проще.
Упадок Греции. После
завоевания Египта римлянами в 31 до н.э.
великая греческая александрийская
цивилизация пришла в упадок. Цицерон с
гордостью утверждал, что в отличие от
греков римляне не мечтатели, а потому
применяют свои математические знания на
практике, извлекая из них реальную
пользу. Однако в развитие самой
математики вклад римлян был
незначителен. Римская система счисления
основывалась на громоздких
обозначениях чисел. Главной ее
особенностью был аддитивный принцип.
Даже вычитательный принцип, например,
запись числа 9 в виде IX, вошел в широкое
употребление только после изобретения
наборных литер в 15 в. Римские
обозначения чисел применялись в
некоторых европейских школах примерно
до 1600, а в бухгалтерии и столетием позже.
ИНДИЯ И АРАБЫ
Преемниками греков в
истории математики стали индийцы.
Индийские математики не занимались
доказательствами, но они ввели
оригинальные понятия и ряд эффективных
методов. Именно они впервые ввели нуль и
как кардинальное число, и как символ
отсутствия единиц в соответствующем
разряде. Махавира (850 н.э.) установил
правила операций с нулем, полагая,
однако, что деление числа на нуль
оставляет число неизменным. Правильный
ответ для случая деления числа на нуль
был дан Бхаскарой (р. в 1114), ему же
принадлежат правила действий над
иррациональными числами. Индийцы ввели
понятие отрицательных чисел (для
обозначения долгов). Самое раннее их
использование мы находим у Брахмагупты (ок.
630). Ариабхата (р. 476) пошел дальше
Диофанта в использовании непрерывных
дробей при решении неопределенных
уравнений.
Наша современная система
счисления, основанная на позиционном
принципе записи чисел и нуля как
кардинального числа и использовании
обозначения пустого разряда, называется
индо-арабской. На стене храма,
построенного в Индии ок. 250 до н.э.,
обнаружено несколько цифр, напоминающих
по своим очертаниям наши современные
цифры.
Около 800 индийская
математика достигла Багдада. Термин «алгебра»
происходит от начала названия книги Аль-джебр
ва-л-мукабала (Восполнение и
противопоставление), написанной в 830
астрономом и математиком аль-Хорезми. В
своем сочинении он воздавал должное
заслугам индийской математики. Алгебра
аль-Хорезми была основана на трудах
Брахмагупты, но в ней явственно
различимы вавилонское и греческое
влияния. Другой выдающийся арабский
математик Ибн аль-Хайсам (ок. 965–1039)
разработал способ получения
алгебраических решений квадратных и
кубических уравнений. Арабские
математики, в их числе и Омар Хайям,
умели решать некоторые кубические
уравнения с помощью геометрических
методов, используя конические сечения.
Арабские астрономы ввели в
тригонометрию понятие тангенса и
котангенса. Насирэддин Туси (1201–1274) в
Трактате о полном четырехугольнике
систематически изложил плоскую и
сферическую геометрии и первым
рассмотрел тригонометрию отдельно от
астрономии.
И все же самым важным
вкладом арабов в математику стали их
переводы и комментарии к великим
творениям греков. Европа познакомилась
с этими работами после завоевания
арабами Северной Африки и Испании, а
позднее труды греков были переведены на
латынь.
Литература:
Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959
Юшкевич А.П. История математики в средние века. М., 1961
Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. М., 1986
Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989 ancient.gerodot.ru Математика в Древней Греции  Разделы: Математика Математика – одна из древнейших, важнейших и
сложнейших компонентов человеческой культуры.
История математики тысячами нитей связана с
историей других наук. Народная мудрость гласит,
что невозможно понять подлинный смысл
настоящего и цели будущего, если не знать и не
ценить прошлое. Жизнь не стояла на месте. С
развитием человечества появляется потребность
передавать известия друг другу, писать, считать.
Так в далёком прошлом постепенно зарождалась
математика. Древние греки были удивительно
талантливым народом, у которого есть чему
поучиться даже сейчас. В те времена Греция
состояла из многих мелких государств. Каждый раз,
когда приходилось решать какой-нибудь важный
государственный вопрос, горожане собирались на
площади, обсуждали его, спорили, а потом
голосовали. Они были хорошими "спорщиками".
По преданию, в то время сложилось утверждение:
" В споре рождается истина!" Греки
отличались трудолюбием и смелостью. Среди них
были отличные строители, мореплаватели, купцы и
художники. Они внесли большой вклад в развитие
культуры и науки, особенно математики. Истории
известно что ученые-математики древней Греции
были крупнейшими математиками в далеком прошлом
и задачи, составленные ими интересны и в наши дни.
Весьма большая часть нашего современного
школьного курса математики, особенно геометрии,
была известна древним грекам. Учитель никогда не
начнет изложения новой темы, не говоря о новом
разделе математики, без вводной исторической
части, вызывающей интерес и внимание учеников.
Уроки с привлечением исторического материала
никого не оставляют равнодушными. Как, знакомя
учеников с начальными понятиями геометрии 7
класса, не рассказать о греческой
математике?..Как изучая тему “Площадь” 8 кл. не
объяснить измерение площадей в Древней Греции
(решение старинных задач). Именно здесь так
устанавливается связь исторических сведений с
материалом рассматриваемой темы. История
математики выступает средством активизации
познавательной деятельности учащихся. А это
является основой учебной деятельности по той
причине, что:
– интерес способствует формированию глубоких
и прочных знаний;
– развивает и повышает качество мыслительной
деятельности, активность в учении,
благоприятствует формированию способностей;
– создает более благоприятный эмоциональный
фон для протекания всех психических процессов.
Экскурс в историю можно сопровождать
картинками, слайдами, презентацией. Математика
со времени её зарождения как науки и много раньше
была тесно связана не только с цивилизацией, с
практикой, но и со всей общечеловеческой
культурой – со всем миром. И математические
теории, и методы открывались, создавались
конкретными личностями, математиками, жизнь и
судьба которых, интересная и насыщенная,
поучительная и порой трагическая, неотделима от
исторической эпохи, в которую они творили.
Ученые Греции

Расскажем о Пифагоре, именем которого названа
теорема, которую знают все. В Древней Греции жил
ученый Пифагор (родился он около 580 г. до н. э.,
а умер в 500 г. до н. э.). О жизни этого ученого
известно немного, зато с его именем связано ряд
легенд. Рассказывают, что он много путешествовал,
был в Индии, Египте, Вавилоне, изучал древнюю
культуру и достижения науки разных стран.
Вернувшись на родину, Пифагор организовал кружок
молодежи из представителей аристократии. В
кружок принимались с большими церемониями после
долгих испытаний. Каждый вступающий отрекался от
своего имущества и давал клятву хранить в тайне
учения основателя. Так на юге Италии, которая
была тогда греческой колонией, возникла так
называемая пифагорейская школа. Пифагорейцы
занимались математикой, философией,
естественными науками. Ими было сделано много
важных открытий в арифметике и геометрии. В школе
существовал декрет, по которому авторство всех
математических работ приписывалось Пифагору.
Пифагор был убит в уличной схватке во время
народного восстания. После его смерти ученики
окружили имя своего учителя множеством легенд,
так что установить о Пифагоре правду невозможно.
Теорема Пифагора имеет богатую историю.
Оказывается, она задолго до Пифагора была
известна египтянам, вавилонянам, китайцам и
индийцам. Доказательство самого Пифагора до нас
не дошло. В настоящее время имеется свыше 100
доказательств. Возможно, что одно из них
принадлежит Пифагору и его ученикам.
Архимед – вершина научной мысли древнего
мира. Архимед родился в 287 году до нашей эры в
греческом городе Сиракузы, где и прожил почти всю
свою жизнь. Отцом его был Фидий, придворный
астроном правителя города Герона. Учился Архимед
в Александрии, где правители Египта Птолемеи
собрали лучших греческих ученых и мыслителей, а
также основали самую большую в мире библиотеку.
Основные работы Архимеда касались различных
практических приложений математики, физики,
гидростатики и механики. В сочинении "Параболы
квадратуры" Архимед обосновал метод расчета
площади параболического сегмента, причем сделал
это за две тысячи лет до открытия интегрального
исчисления. В труде "Об измерении круга"
Архимед впервые вычислил число "пи" –
отношение длины окружности к диаметру – и
доказал, что оно одинаково для любого круга.
Архимед, погибший при захвате римлянами его
родного города Сиракузы в то время, когда пришел
римский солдат. По преданию, Архимед был увлечен
решением геометрической задачи, чертеж которой
был выполнен на песке. Солдат, убивший Архимеда,
или не знал о приказе военачальника сохранить
жизнь Архимеду, или не узнал Архимеда. В наше
время имя Архимеда связывают главным образом с
его замечательными математическими работами,
однако в античности он прославился также как
изобретатель различного рода механических
устройств и инструментов, о чем сообщают авторы,
жившие в более позднюю эпоху. Считается, что
Архимед был изобретателем т.н. архимедова винта,
который служил для подъема воды на поля и явился
прообразом корабельных и воздушных винтов.
- Вызывает сомнение и подлинность истории, что
будто бы царь поручил Архимеду проверить, из
чистого ли золота сделана его корона или же
ювелир присвоил часть золота, сплавив его с
серебром. “Размышляя над этой задачей, Архимед
как-то зашел в баню и там, погрузившись в ванну,
заметил, что количество воды, переливающейся
через край, равно количеству воды, вытесненной
его телом. Это наблюдение подсказало Архимеду
решение задачи о короне, и он, не медля ни секунды,
выскочил из ванны и, как был нагой, бросился
домой, крича во весь голос о своем открытии:
“Эврика! Эврика!” (греч. “Нашел! Нашел!”)”.
- При обороне Сиракуз от осаждавших этот город
римских войск Архимед создал подъемные и
метательные машины, а “зажигательное зеркало”,
с помощью которого он якобы сжег корабли доныне
остается загадкой, волнующей умы исследователей.
- Сохранившиеся математические сочинения
Архимеда можно разделить на три группы.
Сочинения первой группы посвящены в основном
доказательству теорем о площадях и объемах
криволинейных фигур или тел. Сюда относятся
трактаты “ О шаре и цилиндре, Об измерении круга,
О коноидах и сфероидах, О спиралях и О квадратуре
параболы”. Вторую группу составляют работы по
геометрическому анализу статических и
гидростатических задач: О равновесии плоских
фигур, О плавающих телах. К третьей группе можно
отнести различные математические работы: О
методе механического доказательства теорем,
Исчисление песчинок, Задача о быках и
сохранившийся лишь в отрывках Стомахион.
Евклид. Древнегреческий ученый Евклиду
принадлежат сочинения по механике, оптике,
музыке. Известны его заслуги и в астрономии.
Евклиду приписываются также несколько теорем и
новых доказательств
Из дошедших до нас сочинений Евклида наиболее
знамениты “Начала”, состоящие из 15 книг. В 1-й
книге формулируются исходные положения
геометрии, а также содержатся основополагающие
теоремы планиметрии, среди которых теорема о
сумме углов треугольника и теорема Пифагора. При
построении правильных многоугольников опять
звучит это имя Евклида. XIII книга "Начал"
посвящена платоновым телам – правильным
многогранникам, красотой которых восхищаемся на
уроках стереометрии. Рассматривая вопросы
дифференциального и интегрального исчислений на
уроках анализа, говорим о том, что идеи,
положенные в их основу Ньютоном и Лейбницем в XVII
в., уходят своими корнями к методу исчерпывания,
открытому еще Евклидом и Архимедом.
Фалес из Милета (ок.625 – ок.547 до н.э.)
древнегреческий ученый и государственный
деятель, первый из семи мудрецов. Во время
путешествий он посетил Египет, где и
познакомился с астрономией и геометрией. Легенда
рассказывает о том, что Фалес привел в изумление
египетского царя Амазиса, измерив высоту одной
из пирамид по величине отбрасываемой ею тени
Задача. Измерить высоту пирамиды по
отбрасываемой ею тени. (Размеры даны в локтях; 1
локоть = 7 ладоням = 466 мм.)
Зачинатель и родоначальник греческой
философии и науки. Считается, что Фалес первым
доказал несколько геометрических теорем, а
именно:
- вертикальные углы равны;
- треугольники с равной одной стороной и равными
углами, прилегающими к ней, равны;
- углы при основании равнобедренного
треугольника равны;
- диаметр делит круг пополам;
- угол, вписанный в полуокружность, всегда будет
прямым.
Фалес определял высоту предмета по его тени,
расстояния до кораблей, используя подобие
треугольников.
Он сделал ряд открытий в области астрономии,
установил время равноденствий и солнцестояний,
Определил продолжительность года. Фалес был
причислен к группе “семи мудрецов”.
Эратосфен Киренский (ок. 276 – 194 до н.э.) –
разносторонний ученый: математик, астроном,
географ, историк и филолог. Прославился
благодаря изобретению “решета Эратосфена”. В
сочинении “ Решето” Эратосфен создал
оригинальный метод для “отсеивания” простых
чисел. В последовательности натуральных чисел
зачеркнем 1. Число 2-простое. Зачеркнём все числа,
кратные 2. Число 3– первое из незачеркнутых –
простое. Затем зачеркнем всякое число,
делящееся на 3, и т. д. Так можно получить сколь
угодно большой фрагмент последовательности
простых чисел. Во времена Эратосфена писали на
восковых дощечках. Числа не зачёркивали, а
прокалывали. Отсюда и название метода– решето.
Сконструировал прибор – мезолябий для
механического решения делосской задачи
(удвоения куба).
Осуществил первое измерение размеров земли.
Измерив длину 1/50 дуги земного меридиана,
Эратосфен вычислил окружность земного шара и
получил 25 200 стадий, или 39 960 км, что лишь на 319 км
меньше действительного значения.
Герон Александрийский великий физик,
математик, механик и инженер древней Греции. Жил
предположительно в I-II века до нашей эры в
Александрии Египетской. Время жизни отнесено ко
второй половине первого века н. э. на том
основании, что он приводит в качестве примера
лунное затмение 13 марта 62 г. н. э.
Герона относят к величайшим инженерам за всю
историю человечества. Он первым изобрёл
автоматические двери, автоматический театр
кукол, автомат для продаж, скорострельный
самозаряжающийся арбалет, паровую турбину,
автоматические декорации, прибор для измерения
протяженности дорог (древний “таксометр”) и др.
Первым начал создавать программируемые
устройства (вал со штырьками с намотанной на него
веревкой).Одной из главных заслуг Герона
Александрийского перед историей, являются книги,
написанные им. В них описываются не только
собственные изобретения Герона, но и знания
других ученых древней Греции. Много работ Герона
Александрийского было посвящено Математике.
Больше всего в его работах формул по геометрии,
задач по вычислению геометрических фигур. Так же
здесь описывается и знаменитая формула Герона, с
помощью которой можно вычислить площадь
треугольника по трем сторонам.
В конце II в. н.э. начинается закат греческой
математики.
На фоне общего застоя и упадка резко выделяется
гигантская фигура Диофанта.
В III–IV веках нашей эры жил в городе Александрии
знаменитый греческий математик Диофант. Почти
все математики древности занимались
уравнениями. Много внимания им уделял, а главное,
много нового внес в способы их решения
древнегреческий ученый Диофант.
О Диофанте известно очень мало. Есть основание
полагать, что он жил около III в. н.э. Одна группа
уравнений, так называемые неопределенные
уравнения, до сих пор называются диофантовыми
уравнениями. Именно для них он нашел способ
решения.
Скудные сведения о Диофанте может дополнить
нам лишь надпись на надгробном камне,
сформулированная задаДо нас дошли шесть из
тринадцати книг “Арифметики”, написанных
Диофантом, да предание о надписи на его могильном
камне. Эта надпись дает возможность определить
продолжительность жизни математика, которого
позднее назвали “отцом греческой алгебры”.
Здесь погребен Диофант, и камень
могильный
При счете искусном расскажет нам,
Сколь долог был его век.
Велением бога он мальчиком был шестую часть
своей жизни;
В двенадцатой части затем прошла его светлая
юность.
Седьмую часть жизни прибавим – перед нами очаг
Гименея.
Пять лет протекли; и прислал Гименей ему сына.
Но горе ребенку! Едва половину он прожил
Тех лет, что отец, как скончался несчастный.
Четыре года страдал Диофант от утраты такой
тяжелой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть воспринял
Диофант?
Главный труд Диофанта– “Арифметика”, по
предположению, состоит из 13 книг. Книга Диофанта
“Арифметика” содержала большое количество
интересных задач, её изучали математики всех
поколений. Книга сохранилась до наших дней. В
честь Диофанта назван кратер на Луне.О жизни
Метродора, составителя задачи о жизни Диофанта,
ничего неизвестно, нет сведений о времени его
жизни и смерти. В историю математики древней
Греции он вошел как автор задач, составленных в
стихах. Задачи Метродора входили в рукописные
сборники и имели в своё время большое
распространение
Нет сомнений в научности математики Древней
Греции. Ни один народ древности не сделал столько
для развития математики, как жители Греции.
Человеческой природе свойственно уважение к
прошлому. Это уважение иногда вызывает у
учащихся желание взглянуть на математику как на
науку сквозь туман старины, прикоснутся к седой
древности, тысячелетним тайнам и загадкам…
Пускай останется извечный мир загадок
Чтоб продолжалась жизнь, не ведая конца. В. Рождественнский
ПРЕЗЕНТАЦИЯ
Список используемой литературы
- Виленкин Н.Я. и др. За страницами учебника
математики. М. “Просвещение” АО “Учебная
литература” 1996.
- Глейзер Г.И. История математики в школе. М.
“Просвещение” 1995.
- Савин А.П. Энциклопедический словарь юного
математика. М. “Просвещение” 1995.
- Чистяков В. Д. Старинные задачи по элементарной
математике. – Минск: вышэйшая школа, 1978.
- Барвин И. И., Фрибус Е. А. Старинные задачи. Книга
для учащихся. – М.: Просвещение,199
- 3. Болгарский Б.В. Очерки по истории математики.
-2-е иэд., Выш.школа,1979.
- Крыситский В. Шеренга великих математиков –
Варшава: Наша Ксенгарня, 1981.
- Рыбников К.А. История математики – М.:
Просвещение, 1994. – 123 – 125 с.
xn--i1abbnckbmcl9fb.xn--p1ai
|
