Греческая система счисления. Древние греческие цифры
Греческие цифры ВикипедияСистемы счисления в культуре Индо-арабская | АрабскаяТамильскаяБирманская | КхмерскаяЛаосскаяМонгольскаяТайская | Восточноазиатские | КитайскаяЯпонскаяСучжоуКорейская | ВьетнамскаяСчётные палочки | Алфавитные | АбджадияАрмянскаяАриабхатаКириллическаяГреческая | ГрузинскаяЭфиопскаяЕврейскаяАкшара-санкхья | Другие | ВавилонскаяЕгипетскаяЭтрусскаяРимскаяДунайская | АттическаяКипуМайяскаяЭгейскаяСимволы КППУ | Позиционные | 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | | Нега-позиционная | | Симметричная | Смешанные системы | Фибоначчиева | Непозиционные | Единичная (унарная) |
Греческая система счисления, также известная как ионийская или новогреческая — непозиционная система счисления. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϛ (стигма), ϟ (коппа) и ϡ (сампи). Эта система пришла на смену аттической, или старогреческой, системе, которая господствовала в Греции в III веке до н. э. Необходимость сохранять порядок букв ради сохранения их числовых значений привела к относительно ранней (IV век до н. э.) стабилизации греческого алфавита. | 1 α | 10 ι | 100 ρ | | 2 β | 20 κ | 200 σ | | 3 γ | 30 λ | 300 τ | | 4 δ | 40 μ | 400 υ | | 5 ε | 50 ν | 500 φ | | 6 ϝ или ϛ | 60 ξ | 600 χ | | 7 ζ | 70 ο | 700 ψ | | 8 η | 80 π | 800 ω | | 9 θ | 90 ϟ | 900 ϡ |
Пример Данные символы позволяют записать лишь целые числа от 1 до 999, например: - 45 — με
- 632 — χλβ
- 970 — ϡο
См. также Ссылки - J. J. O'Connor, E. F. Robertson. Greek number systems. MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland (январь 2001).
- Титло — программа для перевода греческих ионических чисел
wikiredia.ru Греческая система счисления  Греческая система счисления, или Греческие цифры - непозиционной, аддитивная система счисления, которая использует для представления чисел буквы греческой азбуки. Греческие цифры также известные под названиями: Ионические цифры, Милетский цифры, Александрийские цифры, или Алфавитные цифры. В современной Греции они используются и сейчас для обозначения порядковых числительных, подобно применения римских цифр - системы, популярной на Западе, где для обозначения количественных числительных используются арабские цифры. 1. Система букв Буква Число Буква Число Буква Число Буква Число | α | 1 | ι | 10 | ρ | 100 | ͵ Α | 1000 | | β | 2 | κ | 20 | σ | 200 | ͵ Β | 2000 | | γ | 3 | λ | 30 | τ | 300 | ͵ Γ | 3000 | | δ | 4 | μ | 40 | υ | 400 | ͵ Δ | 4000 | | ε | 5 | ν | 50 | φ | 500 | ͵ Ε | 5000 | | ϝ или ς или στ | 6 | ξ | 60 | χ | 600 | ͵ Ϛ | 6000 | | ζ | 7 | ο | 70 | ψ | 700 | ͵ Z | 7000 | | η | 8 | π | 80 | ω | 800 | ͵ H | 8000 | | θ | 9 | ϟ | 90 | ϡ | 900 | ͵ Θ | 9000 |
2. Объяснение и примеры В новогреческом языке принято использовать прописные буквы, например: греч. Φίλιππος Β 'ο Μακεδών - Филипп II Македонский или греч. Ἀλέξανδρος Γ 'ὁ Μακεδονικός - Александр III Македонский. Греческая система счисления, в отличие от римской, - непозиционной аддитивная система счисления, поэтому выражения 45 = με и 45 = εμ тождественны. Число образуется как сумма цифр, если оно меньше 10 000. Иначе используют специальный символ М. Он означает тысячу, и работает подобно современному экспоненциального формата записи чисел с плавающей запятой (например 0.5e-06). Это позволяет записать большие числа. Примеры чисел: 45 - με, 632 - χλβ, 970 - Ϡ ο, 9128 - ͵ Θρκη, и самое интересное 2056839184 - βΜκ ͵, αΜ ͵ εχπγ, ͵ θρπδ. См.. также nado.znate.ru Древняя греческая нумерация — МегаЛекции В древнейшее время в Греции была распространена так называемая Аттическая нумерация. В этой нумерации числа 1, 2, 3, 4 изображались соответствующимколичеством вертикальных полосок: 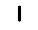 , , 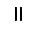 , , 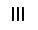 , , 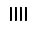 .Число 5 записывалось знаком .Число 5 записывалось знаком 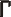 (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте". Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте". Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: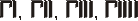 . . Число 10 обозначалось 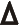 - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000. - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000. Примерно в третьем веке до нашей эры аттическая нумерация в Греции была вытеснена другой, так называемой "Ионийской" системой. В ней числа 1 - 9 обозначаются первыми буквами греческого алфавита: 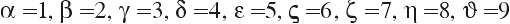
числа 10, 20, … 90 изображались следующими девятью буквами:ѓ 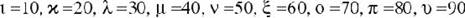 числа 100, 200, … 900 последними девятью буквами: 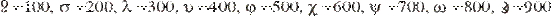 Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше. Для отличия цифр и букв писали черточки над цифрами. Примерно по такому же принципу организованную систему счисления имели в древности евреи, арабы и многие другие народы Ближнего Востока. Вавилонская нумерация Первой известной нам позиционной системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2500≈2000 лет до н. э. Основанием ее служило число 60. В древнем Вавилоне примерно за 40 веков до нашего времени создалась позиционная нумерация, то есть такой способ записи чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой. Наша теперешняя нумерация тоже поместная. В вавилонской поместной нумерации ту роль, которую у нас играет число 10, играет число 60, и потому эту нумерацию называют шестидесятиричной. Числа менее 60 обозначались с помощью двух знаков: 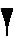 для единицы, и для единицы, и  для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например 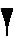 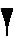 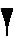 - 3; - 3;   - 20; - 20;    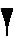 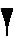 - 32 - 32
а это число 59. Вавилонский способ обозначения чисел больше 60 очень похож на наш: В этом случае цифры записываются по разрядам, с небольшими пробелами между: Так записывается число 302, то есть 5´60+2 А это 1´60´60+2´60+5 = 3725 При отсутствии разряда вставлялся значек 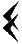 , игравший роль нуля. , игравший роль нуля. это запись числа 7203 (2´60´60+3) Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3´60 записывалось так 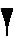 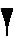 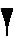 , а обозначать эта запись могла и 3, и 180, и 10800 (3´60´60), и т. д. Различать эти числа можно было только по смыслу текста. , а обозначать эта запись могла и 3, и 180, и 10800 (3´60´60), и т. д. Различать эти числа можно было только по смыслу текста.
Шестидесятеричная система счисления появилась у вавилонян позже десятеричной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор неизвестно, когда и как возникла у вавилонян шестидесятеричная система. На этот счет строилось множество гипотез, но ни одна не доказана. Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: Ближний Восток, Средняя Азия, Северная Африка, Западная Европа пользовались ими. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т. е. До начала XVII века. Следы шестидесятеричных дробей сохраняются и поныне в делении углового и дугового градуса (а также часа) на 60 минут и минуты на 60 секунд. Нумерация индейцев Майя Эта нумерация очень интересна тем, что на ее развитие не повлеяла ни одна из цивилизаций Старого Света. Однако в ней использованы все те же принципы. Сначала эта нумерация обслуживала пятиричную систему счисления, а потом ее приспособили для двадцатиричной. Записывались цифры числа в столбик, начиная со знаков  , затем знаки , затем знаки  , а потом , а потом  больших значений и заканчивая меньшими. больших значений и заканчивая меньшими. 20+20+5+5+5+1+1+1+1 = 59; 5+5+5+1 = 16; 20+1+1+1 = 23 Такая запись числа аддитивна, то есть в ней используется только сложение:
megalektsii.ru
|
