Системы счисления разных народов. Древнейшие системы счисления
История систем счисления Цифры, то есть условные знаки для обозначения чисел, которыми мы сейчас пользуемся, были изобретены в Индии. В Европу они попали при посредничестве арабов, у которых мы заимствовали и слово «цифра», первоначально означавшее «ноль, пустое место». В древности, чтобы что-нибудь посчитать, людям было достаточно пальцев на руках и ногах. Если они хотели зафиксировать полученный результат, то делали отметки на конце палки, костях животных или камне. С течением времени расчеты усложнялись: торговцам надо было точно знать, что и в каком количестве они продавали или покупали, а чиновникам - какие налоги собирали и на что их тратили. Записывать большие числа при помощи меток становилось неудобно, и поэтому были изобретены цифры. Считается, что первую систему специальных знаков для записи чисел придумали в Египте около 3400 г. до н. э. Роль цифр выполняли иероглифические символы, которые обозначали числа 1, 10, 100 и так далее до миллиона. Повторяя один и тот же символ или комбинируя их, можно было записать числа, некратные десяти. Порядок расположения символов при этом не имел значения: их писали как справа налево, так и слева направо или даже вертикально. Первая позиционная система цифр, в которой значение символа зависело от его местоположения в записи, была создана шумерами примерно в том же 3400 г. до н. э. Жители острова Крит начали использовать цифры около 1200 г. до н. э. В критских надписях, так же как в египетских, числа передавались на письме по десятичному принципу - с использованием отдельных знаков для единиц (вертикальная черта), десятков (горизонтальная черта), сотен (круг), тысяч (круг с расходящимися от него в разные стороны четырьмя лучами) и десятков тысяч (круг с расходящимися от него четырьмя лучами и горизонтальной чертой внутри). В IV в. до н. э. в Китае была создана позиционная система записи, в которой были специальные знаки для чисел от 1 до 9, а также для 10,100 и 1000. Древние греки использовали для обозначения единицы вертикальную черту, а для 5,10,100,1000 и 10000 - знаки Г, Д, Н, X и М, представляющие собой заглавные буквы слов, называющих соответствующие числа. Эта система впервые появилась на территории Аттики около 600 г. до н. э. и известна под названием аттических цифр. Примерно с III в. до н. э. она была вытеснена другой, так называемой ионийской системой. В ней числа от 1 до 9 обозначались первыми буквами греческого алфавита, десятки от 10 до 90 - следующими девятью буквами, а сотни от 100 до 900 - последними девятью буквами. Для того чтобы отличать числа от слов, над буквами ставили горизонтальную черту. Наиболее долговечной из древних систем записи чисел оказалась римская, до сих пор используемая в некоторых случаях. Она состоит всего лишь из 7 знаков: 1=1, V=5, Х=10, L=50, С=100, D=500 и М=1000. Индо-арабские цифры, которые мы используем сегодня, появились в Индии, вероятно, в IV в. до н. э. Первым свидетельством об индийской десятичной позиционной системе счисления являются слова христианского епископа Севера Себохта, жившего в одном из монастырей в верховьях Евфрата в VII в. Арабские ученые начали использовать индийские цифры примерно в VII в. Первая европейская рукопись с индо-арабскими цифрами появилась в Испании в 976 г. Многие культуры, включая нашу, пользуются системой счисления с основанием 10. Этот выбор является вполне естественным, поскольку у человека 10 пальцев, но не единственным.  Копия римской счетной доски, или абака. В этом типе счетной доски костяшки скользят в желобках, а не на прутьях (в отличие от более позднего китайского абака, называемого суаньпань).  На этом древнеримском надгробии изображен мальчик (крайний слева) с абаком в руках.  «Подсчет гусей». На египетской фреске примерно 1350 г. до н. э. изображено, как писец (внизу слева) проверяет цифры на папирусном свитке. У него под мышкой находится табличка для письма. В Папуа-Новой Гвинее и Австралии есть племена, которые считают следующим образом: «один, два, два-и-один, две двойки, два-и-два-и-один» и т. д. Это бинарная система счисления с основанием 2. Основанием системы счисления индейцев майя было 20; а у некоторых народов основанием было 12. Например, в Великобритании вплоть до 1971 г. использовали двенадцатеричную счетно-денежную систему (12 пенсов составляли 1 шиллинг), а в Северной Америке до сих пор используется двенадцатеричная система при измерении длины (12 дюймов равняются 1 футу). Кроме того, некоторые товары (яйца, бутылки пива, столовые приборы и сервизы) традиционно считают дюжинами (по 12). У шумеров основанием системы счета было 60, следы этого сохранились в современном измерении времени и углов - мы считаем, что в часе 60 минут, в минуте 60 секунд, а окружность делится на 360 градусов. 16.07.2018 altpp.ru Древние системы счисления - INDRIKДревние системы счисления http://mirovid.profiforum.ru/t95-topic#161 Древние системы счисления отличаются большим разнообразием, поскольку привычный нам способ записи чисел с помощью десяти знаков появился далеко не сразу. Прежде всего надо отметить, что существовали две основные системы счисления - пятеричная и привычная нам десятеричная. Кроме них, существовала так же 12-ричная, которая в Англии вплоть до 19 века вообще главенствовала. Из Древнего Вавилона пришла к нам и 60-ричная система счисления, которая применяется до сих пор при измерении угловых величин - круг, состоящий из 360 градусов делится без остатка на многие удобные цифры. Стоит отметить, что в древние системы счисления ряда народов прослеживаются остатки более древней пятеричной системы - у древних римлян и майя например. Разнообразие в на самом деле небольшое - в основном десятичная или пятерично-десятичная. Но, вот когда дело доходило до записи на бумаге или камне, то тут, как говорится, каждый был сам себе голова. Академий наук тогда не было, министерств тоже, о стандартах школьного образования тем более никто не слыхивал, китайцы знали о достижениях греков мягко говоря маловато, и наоборот. Поэтому, каждый изобретал свой способ записи. Пожалуй самым древним обозначением числа можно считать вертикальную палочку. Почти у всех древних народов она естественным образом изображала единицу. Дальше шли соответственно две, три, реже четыре палочки. Дальше в основном вводили новые знаки по достижении какого-то числа, при котором записывать большое числа палочек было просто неудобно. Например римляне (по другим сведениям этруски) ввели знак "V" для числа пять, напоминающую сомкнутую ладонь с пятью пальцами при отведённом большом пальце, получив раннюю пятеричную систему счисления. Но, пятёрки было мало, поэтому ввели ещё "Х" - десять, а в последствии и остальные известные нам знаки для промежуточных чисел. Получилась известная нам непозиционная римская система счисления, когда нужное число набиралось сложением числовых значений ограниченного набора знаков. Большие числа у римлян обозначались довольно своеобразно - например посмотрите 1000000 римскими цифрами. Подробнее о римских цифрах. Древние майя придумали систему счисления, подчинив её нуждам астрономических расчётов - двадцатиричную. В ней появилось понятие разряда, причём в одном из разрядов был введён изъян, чтобы получить число 360, близкое к числу дней в году - 365. Единицу обозначали точкой, а пять - чёрточкой. Они так же самостоятельно ввели понятие нуля, который обозначали в виде ракушки. Это двадцатирично-пятеричная система. Подробнее о числах майя. Инки в Южной Америке придумали вообще уникальную сисему счисления - типу - числа обозначались узелками на шнурках! Различалась форма узелков, цвет шнурков, их расположение на шнурке. Система была довольно сложной, требовала специального обучения, но она вполне удовлетворяла инков, позволяя вести даже двойной счёт в бухгалтерии! Древняя система счислений у китайцев тоже была палочковой, как у римлян, причём не одна. Впоследствии она была заменена иероглифической десятичной системой счисления. В ней каждому разряду десятков, сотен и тысяч соответствовал свой иероглиф, рядом с которым ставился иероглиф их количества со значением от 1 до 9. Так же, китайские математики ввели понятие нуля, но несколько нулей подряд не писали, ограничиваясь одним, что остановило их в полушаге от введения полноценной позиционной системы. Ведь стоило написать два нуля вместо одного в числе 1001 и сразу стало бы ясно, что иероглиф "тысяча" лишний! Жаль - проделав большую работу, они остановились в полушаге от открытия. Впрочем, - "Восток - дело тонкое". Получилась десятичная "почти-позиционная" система счисления - каждый разряд записывался двумя знаками. Вот 2012 по-китайски: Подробнее о китайских цифрах. В Древнем Египте бытовала десятичная система счисления и существовало несколько систем обозначения чисел. Иероглифическая форма записи, когда для всех степеней десяти, включая единицу, был свой знак. Подобно другим системама счисления, любое число можно было обозначить сложением числовых значений этих знаков. Это "парадная", довольно громоздкая форма записи, поэтому существовала жреческая (иератическая) система счисления, в которой для единиц, десятков и т.д. были отдельные знаки. Складывать в такой записи тоже приходилось, но надпись была заметно короче. Позднее возникло ещё более простое демотическое письмо. Пока египетские системы счисления в моём переводчике чисел "Титло" не сделаны, по причине затруднений с кодировками и шрифтами для древнеегипетских надписей. С появлением алфавита в странах Средиземноморья, возникла возможность использовать буквы для обозначения чисел. Десятичная система там уже устоялась, поэтому поступали достаточно просто - первые 9 букв обозначали цифры 1-9, вторые 9 букв обозначали десятки от 10 до 90, а оставшиеся обозначали сотни. Нужное число набиралось из числовых значений этих букв. Неприятность была в том, что в ранних алфавитах букв было маловато. Например в еврейском алфавите наибольшей сотней было 400, а 500 приходилось записывать уже двумя буквами - 100+400. В армянском алфавите букв было гораздо больше - хватило и для сотен, и для всех тысяч, для десятков тысяч сверху буквы ставилась чёрточка. А, у грузин нашлась отдельная буква даже для 10000 (по-моему это рекорд в алфавитной записи чисел: 20000 где-то проскакивало, но смутно). В кириллице букв тоже было в избытке, но в противоположность армянам и грузинам, наши предки ограничились единицами, десятками и сотнями, а для тысяч ввели подстрочный знак для умножения цифры в 1000 раз. Для больших степеней десяти существовал вообще уникальный способ обозначения - буква окружалась точками, крестиками и лучиками. Наибольшим числом было 10 в степени 49 (остаётся только догадываться зачем...). Подробнее о записи чисел кириллицей. Однако, в глаголице всё-же пошли привычным путём - присвоили старшим буквам азбуки "тысячные" значения. Подробнее о записи чисел глаголицей. Настоящей переворотом стало открытие полноценного понятия нуля индийскими математиками. Благодаря этому появилась привычная нам десятичная ПОЗИЦИОННАЯ система счисления, рассказывать о которой нет особого смысла. Во многих странах существуют свои обозначения для чисел, но на поверку - все они отличаются друг от друга только внешним видом знаков(цифр) и не более того. (опубликовано на http://info-7.ru) Оригинал записи и комментарии на LiveInternet.ru rusislav.livejournal.com История математики. Древние системы счисления.Слайд 1 Автор: Раздобурдин Сергей Дмитриевич Razdoburdin Sergei Руководитель: Сенаторова Ляна Георгиевна Учитель математики Россия, Кемеровская область, г. Новокузнецк МБОУ «Средняя общеобразовательная школа №71» История математики « ИСТОРИЯ МАТЕМАТИКИ »Слайд 2 Работа посвящена изучению истории математики не только как науки, но и как системы обработки чисел. В процессе изучения было использовано несколько древних систем счисления, многие из которых существуют и по сей день. Основной частью работы является изучение древних систем счисления. Слайд 3 Предупреждение При виде значков, показанных ниже - нажимать на них (но не сейчас): Остальные кнопки будут описаны при просмотре. Слайд 4 Содержание: Введение История развития математики Арабская система счисления Римская система счисления Кириллическая система счисления Фотогалерея Итог Источники Слайд 5 Введение Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Дальнейшее развитие математики началось примерно в 3000 г. до н.э. благодаря вавилонянам и египтянам. Эй! Я тут! Слайд 6 История развития математики. Развитие математики началось вместе с тем, как человек стал использовать абстракции. К примеру, простую абстракцию — числа; понимание того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Древние люди не только узнали, как считать определённые объекты, но также осознали, как вычислять еще и абстрактные количества, такие, как время: дни, сезоны. Из элементарного счёта постепенно начала развиваться арифметика: сложение, вычитание, умножение и деление чисел. Слайд 7 Прогрессирование математики опирается на письменность и умение записывать числа. Скорее всего, древние люди первоначально выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея другой системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса , созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля. Слайд 8 Исторически, основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений. Для того, чтобы что-то посчитать, мы постоянно пользуемся числами, составленными в свою очередь из цифр. Встречаясь с цифрами на каждом шагу, мы настолько привыкли к их существованию, что вряд ли задумываемся, а откуда же они взялись. А, между прочим, история их возникновения чрезвычайно увлекательна. Слайд 9 Сначала были…пальцы . Весьма универсальное, удобное и сподручное средство для счёта. Его используют и до сих пор, правда, лишь в том случае, если нужно показать небольшое, ограниченное одним десятком число (здесь учитываем лишь возможности рук, пальцы ног не в счёт). Не удивительно, что очень быстро назрела потребность в других, более совершенных символах счёта . Слайд 10 Первое подобие цифр возникло около пяти тысяч лет назад в Египте и Месопотамии и представляло собой засечки на дереве или камнях. Египетские жрецы использовали для письма папирус, а в Месопотамии для этих целей служила мягкая глина. Цифры тех времён обозначались чёрточками для единиц и различными другими метками для десятков и более высоких порядков. Интересно то, что записи носили не только счётный характер, но и математический: древние египтяне, как известно, достигли потрясающих высот в арифметике и геометрии. Когда появились иероглифы, цифры стали записывать через них. Чтобы увеличить картинку – кликните на неё. Слайд 11 Следующий этап в истории цифр принадлежит древним римлянам. Изобретенная ими система исчисления основана на использовании букв для отображения чисел. Так, они применяли в своей системе буквы «I», «V», «L», «C», «D», и «M ». Не всем для записи чисел понадобилось столько символов. Например, майя в первом тысячелетии нашей эры писали любое число, используя лишь три знака: точку, линию и эллипс. Точка означала единицу, линия имела значение пяти, а эллипс, находясь под любым из этих знаков, увеличивал его значение в двадцать раз. Подобная минимизация отнюдь не приводила к упрощению записи: для обозначения того или иного числа приходилось использовать длинные ряды символов. Вернуться к содержанию Слайд 12 Современные привычные для нас цифры имеют арабское происхождение. Хотя арабы в свою очередь заимствовали их у индусов, видоизменив их и приспособив к своему письму. Характер написания каждой из девяти арабских цифр хорошо прослеживается, если записать их в «угловатой» форме. Количество углов каждой цифры соответствует количеству, которое эта цифра обозначает. Привычные нам формы арабских цифр более округлые – влияние скорописи. Арабские цифры возникли в Индии, не позднее V века. Тогда же было открыто и формализовано понятие нуля ( шунья ), которое позволило перейти к позиционной записи чисел. Данную картинку тоже можно увеличить. Слайд 13 Традиционные арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму. Индийскую систему записи широко популяризировал учёный ал-Хорезми, автор знаменитой работы « Китаб ал- джабр ва -л- мукабала », от названия которой произошёл термин «алгебра ». Арабские цифры стали известны европейцам в X вв. Благодаря тесным связям христианской Барселоны и мусульманской Кордовы, Сильвестр II (папа римский с 999 по 1003 годы) имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности, он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления и начал пропагандировать их внедрение в европейскую науку. Вернуться к содержанию Слайд 14 Римские цифры появились за 500 лет до нашей эры у этрусков . Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Пример: число 1988. Одна тысяча - M, девять сотен - CM, восемь десятков - LXXX, восемь единиц - VIII. Запишем их вместе: MCMLXXXVIII. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая — перед большей, то меньшая вычитается из большей. Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры . Слайд 15 Римские цифры 1 I лат. unus 5 V лат. quinque 10 X лат. decem 50 L лат. quinquaginta 100 C лат. centum 500 D лат. quingenti 1000 M лат. mille Слайд 16 Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту. Иногда черту рисовали и сверху, и снизу - в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз . Существует «сокращённый способ» для записи больших чисел, таких как 1999. Он не рекомендуется, но иногда используется для упрощения. Отличие состоит в том, что для уменьшения цифры слева от неё может писаться любая цифра, например 999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX. Слайд 17 Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую « IV» прочесть труднее, чем «IIII ». Часы на Спасской башне, как пример неудобства. Слайд 18 Другая версия: Для записи целых чисел в римской нумерации используются семь основных чисел: I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000. При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трех раз, таким образом с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX ). В ранние периоды существовали знаки для обозначения бо́льших цифр - 5000, 10000, 50000 и 100000 (тогда максимальное число по упомянутому правилу равно 399999). Слайд 19 По-римски число 94 будет XCIV=100-10+5-1=94 - так называемое "правило вычитания" (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 - как XXXX). Существует шесть вариантов использования "правила вычитания": IV = 4 IX = 9 XL = 40 XC = 90 CD = 400 CM = 900. Необходимо отметить, что другие способы "вычитания" не допустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел. Слайд 20 С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта . Вернуться к содержанию Слайд 21 Кириллическая система счисления. В основных чертах повторяет греческую систему счисления. Использовалась в России до начала XVIII века, когда была заменена на систему счисления, основанную на арабских цифрах. В настоящее время используется в книгах на церковнославянском языке. А почему бы и не увеличить? Слайд 22 Примеры записи чисел кириллицей: Большинство букв древнерусского алфавита имели числовое соответствие. Так, буква «Аз» означала «один», «Веди» — «два»… Некоторые буквы числовых соответствий не имели. Числа писались и произносились слева направо за исключением чисел от 11 до 19 (например, 17 — сем-на- дцать ). По такому же принципу строилась глаголическая система счисления, в которой использовались буквы глаголицы. В начале XVIII века иногда применялась смешанная система записи чисел, состоящая и из кириллических, и из арабских цифр. Например, на некоторых медных копейках отчеканена дата 17К1 (1721 ). Вернуться к содержанию Слайд 23 Фотогалерея В данном разделе будут показаны картинки и фотографии, встречающиеся в презентации, только здесь они показаны крупным планом. Слайд 24 Территория Египта и Месопотамии . Слайд 25 Арабские цифры. Слайд 26 Часы на Спасской башне. Слайд 27 Кириллические цифры и числа . Слайд 28 Итог: В ходе работы мы познакомились с историей математики, узнали о некоторых системах счисления и их истории. Слайд 29 Источники: http:// knu.znate.ru/docs/index-500746.html http:// go.mail.ru/search_images?fr=mainVertical nsportal.ru Системы счисления разных народов
В Древнем Вавилоне примерно за 40 веков до нашего времени создалась по-местная (позиционная) нумерация, т.е. такой способ изображения чисел, при котором одна и та же цифра может обозначать разные числа в зависимости от места, занимаемого этой цифрой. Наша современная нумерация тоже поместная: в числе 52 цифра 5 обозначает пятьдесят, т.е.5х10, а в числе 576 эта же цифра обозначаёт пятьсот, т.е. 5х10х10. В вавилонской поместной нумерации ту роль, которую играет у нас число 10, играло число 60, и потому эту нумерацию называют шестидеситеричной. Числа, меньшие 60, обозначались с помощью двух знаков. Они имели клинообразный вид, так как вавилоняне писали на глиняных дощечках палочками треугольной формы. Эти знаки повторялись нужное число раз.
Шестидесятеричная система возникла позднее десятичной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор неизвестно, когда и как возникла у вавилонян шестидесятеричная система. На этот счет строилось много гипотез, но ни одна пока не доказана. Мнения историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы. Первая исходит из того, что произошло слияние двух племен, одно из которых пользовалось шестеричной, другое — десятичной. Шестидесятеричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса. Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60.
Шестидесятеричная запись целых чисел не получила распространения за пределами ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: в страны Ближнего Востока, Средней Азии, в Северную Африку и Западную Европу. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т.е. до начала XVII в.
3.2 Римская пятеричная

Это, наверное, самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме.
|
I |
1 | |
V |
5 | |
X |
10 | |
L |
50 | |
C |
100 | |
D |
500 | |
M |
1 000 |
Предполагаемое происхождение римских цифр

Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать не удобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание. Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.
О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века.
В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.
3.3 Древнегреческая аттическая пятеричная
В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции – Аттики со столицей Афины.
В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок:  , ,  , ,  , ,  . Число 5 записывалось знаком . Число 5 записывалось знаком  (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:

Число 10 обозначалось  - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно: - заглавной "Дельта" от слова "дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:

3.4 Древнегреческая ионийская десятеричная алфавитная
Примерно в третьем веке до нашей эры аттическая система счисления в Греции была вытеснена другой, так называемой "Ионийской" системой (она возникла в Милеете – греческая малоазиатская колония Ионии). В ней числа 1 - 9 обозначаются первыми буквами древнегреческого алфавита:

числа 10, 20, … 90 изображались следующими девятью буквами:

числа 100, 200, … 900 последними девятью буквами:

Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами.

Древние евреи, арабы и многие другие народы Ближнего Востока имели такие же системы счисления.
При ее помощи можно было просто записать числа до ста миллионов (100 000 000). Эта система по быстроте счета мало отличается от «арабской». И хоть она не позиционная, но в ней есть мультипликативность.
3.5 Славянская глаголическая десятеричная
Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.
|
 1 1
|
 10 10
|
 100 100
|
 1 000 1 000
| |
 2 2
|
 20 20
|
 200 200
|
| |
 3 3
|
 30 30
|
 300 300
|
| |
 4 4
|
 40 40
|
 400 400
|
| |
 5 5
|
 50 50
|
 500 500
|
| |
 6 6
|
 60 60
|
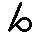 600 600
|
| |
 7 7
|
 70 70
|
 700 700
|
| |
 8 8
|
 80 80
|
 800 800
|
| |
 9 9
|
 90 90
|
 900 900
|
|
Числа записывали из цифр так же слева, направо, от больших к меньшим цифрам. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Такая запись числа аддитивная, то есть в ней используется только сложение:
   = 800+60+3 = 863 = 800+60+3 = 863
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.
3.6 Славянская кириллическая десятеричная алфавитная
Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:

Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:
 = 800+60+3 = 800+60+3
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
|

|
Тысяча |
1000 | |

|
Тьма |
10 000 | |

|
Легион |
100 000 | |

|
Леодр |
1 000 000 | |

|
Ворон |
10 000 000 | |

|
Колода |
100 000 000 |
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
3.7 Древнеиндийские системы счисления
Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.

Наряду с этой системой существовала в Индии еще одна система счисления брахми.

Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы.
В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны. anastasi-shherbakova.narod.ru
|
