14 доказательств того, что в древней Индии любили математику. Алгебра в древней индии
О математике древней Индии — Колпаков Александр Николаевич Индия имеет большую и богатую самобытную культуру, начало которой уходит в седую древность. Много тысяч лет тому наза, еще до нашей эры, в Индии городские водосточные системы и оросительные каналы, строились многоэтажные здания из хорошо обожженного кирпича. В далеком прошлом индийцы владели искусством керамического производства (производство изделий обожженной глины), умело пользовались гончарным кругом, успешно развивали ювелирное дело (изготовление изделий из драгоценных камней и металлов). Еще в глубокой древности Индия славилась знаниями в области астрономии, грамматики и других наук. Наибольших успехов Индийские ученые достигли в области математики. Они явились основоположниками арифметики и алгебры, в разработке которых пошли дальше греков. Величайшим достижением древнеиндийской математики является, прежде всего, открытие позиционной системы счисления, состоящей из десяти индийских цифр, включая и знак нуль, называемый по-индийски «сунья», что дословно означает «ничто». Интересно заметить, что в первоначальном начертании нуль изображался точкой и лишь спустя много веков – в виде маленького кружка. Кто первый из индийских ученых стал употреблять десятичную систему, неизвестно точно. Однако есть основание думать, что эта система была изобретена в начале первого века нашей эры. Что касается первого употребления знаку нуля, то это факт относится ко второму веку нашей эры. Наиболее известными индийскими математиками являются Ариабхата (конец 1 века) , Брахмагупта (7 век) и Бхаскара (12 век). Индийские математики далекого прошлого любили состязаться на публичных народных собраниях. По этому поводу один индийский автор 7 века, заканчивая свою книгу, писал: «Подобно тому, как солнце затмевает своим блеском звезды, так мудрец затмевает славу других людей, предлагая и особенно решая на народных собраниях математические задачи». Заметим, что все указания и решения к индийским задачам даются сейчас в современной символике. Задачи древней Индии: 1) Из четырех жертвователей второй дал вдвое больше первого. Третий дал втрое больше первого, четвертый в четверо больше первого, а все вместе они дали 132 монеты. Сколько монет дал первый. Эта задача взята из бахшалийской рукописи, найденной в 1881 году при раскопках в Бахшали в северо-западной Индии. Рукопись выполнена на березовой коре и относиться к 3-му или 4-му веку нашей эры. Ученые-математики установили, что эта рукопись является неполной копией боле древних математических рукописей. 2) Пятая часть пчелиного роя села на цветок кадамба, Треть — на цветокх силиндха. Утроенная разность последних двух чисел пчел направилась к цветам кутая и осталась еще одна маленькая пчелка, летающая взад и вперед, привлеченная ароматом жасмина и пандуса. Спрашивается, сколько всего пчел. Задача присутствует в трактате «сущность вычисления» («Ганитасара») индийского математика Сридхары, жившего в промежутке 7-10 в.в. Время жизни точно не установлено. (Сридхара является автором ряда задач, которые широко использовались индийскими математиками последующих времен. 3) Два светила находятся на данном расстоянии (d) друг от друга, движутся одно к другому с данными скоростями 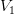 и и 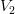 . Определить точку их встречи. . Определить точку их встречи. Задача взята из трактата «Ариабхатиам» известного индийского математика конца 5-го – начала 6-го века Ариабхаты. Этот трактат посвящен астрономии и математике. В его математической части Ариабхата дает ряд правил по арифметики, алгебре, геометрии и тригонометрии, нужных для астрономии и в первую очередь составления астрономических страниц. Ариабхата является автором многих задач по элементарной математике, одна из которых и приводится. Подборка задач и оформление:Колпаков Александр, репетитор по математике. ankolpakov.ru 14 доказательств того, что в древней Индии любили математику — Индийская гостиная Математика часто является одним из самых страшных и ненавистных предметов в школе. Тем не менее, народ древней Индии очень любил этот предмет и сделал множество великих открытий и изобретений, которые выдержали серьезное испытание временем и дошли до наших дней. Математика для древних индийцев всегда была частью повседневной учебной программы. Благодаря этому страна вырастила немало замечательных ученых, который сделали огромный вклад в эту науку. Вот несколько доказательств этого факта: 1. Жители земель возле Саптах-Синдху вели высоко организованный образ жизни. Дренажная система, зернохранилища, доки и дома древнеиндийского города Хараппы продолжают изумлять археологов, которые считают эти конструкции геометрическим чудом. 2. Установлено, что геометрия была впервые изучена древними индийцами — синтетический подход к геометрии можно проследить еще в Шульба-сутрах (800 г. до н. э. — 200 г. н. э.), где содержатся данные по сооружению алтаря для жертвенного огня. 3. В Веданга-джйотише, содержащей правила отслеживания движения солнца и луны, высоко оценивается роль математики (ганиты) в ряду других наук. Она сравнивается с гребешком павлина или капюшоном кобры, что символизирует нахождение на самой вершине. 4. Именно выдающийся индийский математик и астроном Арьябхатта вычислил значение числа «пи» как 3,1416, а также длину солнечного года 365.3586805.11 5. Индийцы подарили миру число ноль. 6. Надпись, найденная в городе Аллахабад, является свидетельством того, что десятичная система была в ходу в Индии еще в 5 веке нашей эры. 7. Математик Шридхарачарья точно вычислил значение квадратного уравнения. Его решение было общепризнанно уже в 1025 году н.э. 8. Тригонометрия зародилась в древней Индии. Путешествуя из Индии на Ближний Восток, она дошла до Европы, а затем и до всего мира. 9. В астрономических работах древних индийцев впервые введена функция синуса. 10. Вардхамана Махавира, 24-ый тиртханкара (человек, достигший просветления) в джайнизме, был великим математиком. В своей работе «Ganitasara Sangarah» он отмечает, что отрицательная величина не имеет квадратного корня. 11. Махавира и другие джайнские ученые рассмотривали концепцию перестановок и комбинаций как отдельную ветвь математики, назвав ее викалпа. Она стала предком современной комбинаторики. 12. Известный хирург древней Индии Сушрута Самхита в своей работе дал 63 различных комбинаций шести основных вкусов, а именно Amla (кислый), Tikta (горький), Kashay (вяжущий), Katu (едкий), Lavan (соленый), и Madhur (сладкий). 13. Историки также приписывают математикам Арьябхатте, Брахмагупте, Махавире и Бхаскаре создание формул суммы квадратов и кубов чисел. 14. Арьябхатта открыл формулу для нахождения суммы n членов арифметической прогрессии. indianroom.ru 2. Математика Древней и Средневековой Индии. Математика в средние века Похожие главы из других работ: 10 способов решения квадратных уравнений 1.3 Квадратные уравнения в Индии Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.)... Графики и их функции 1.4 Возникновение и понятие функции в Древней Греции В Древней Греции наука приняла иной характер, чем в Египте и в Вавилоне. Появились профессиональные ученые, которые изучали саму математическую науку, занимались строгими логическими выводами одних утверждений из других. Многое из того... Знаменитые задачи древности: удвоение куба Глава 2. Решение задачи в Древней Греции после Архита. Решение с помощью конических сечений Возможно, в связи с тем, что задача об удвоении куба продолжала привлекать к себе внимание ученых, а решение ее Архитом представлялось им сложным... История математики 1. ГРЕЧЕСКАЯ МАТЕМАТИКА Классическая Греция. С точки зрения 20 в. родоначальниками математики явились греки классического периода (6-4 вв. до н.э.). Математика, существовавшая в более ранний период, была набором эмпирических заключений. Напротив... История математики 4. СОВРЕМЕННАЯ МАТЕМАТИКА Создание дифференциального и интегрального исчислений ознаменовало начало «высшей математики». Методы математического анализа, в отличие от понятия предела, лежащего в его основе, выглядели ясными и понятными. Многие годы математики... История развития математики 2. Греческая математика ... История развития математики 5.4 Современная математика Создание дифференциального и интегрального исчислений ознаменовало начало "высшей математики". Методы математического анализа, в отличие от понятия предела, лежащего в его основе, выглядели ясными и понятными. Многие годы математики... Квадратные уравнения и уравнения высших порядков 1.3 Уравнения в Индии Квадратные уравнения решали и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 году индийским математиком и астрономом Ариабхаттой. Другой индийский ученый... Математика в древнем Китае Математика Китая Техника Вычислений. Мало известна техника вычислений древнего Китая, которую иногда совсем не упоминают, хотя существенным образом дополняет общую картину развития математики в древности... О пифагорейской математике 1.2.1 Математика Пифагорейцы создали науку о числе, положили начало арифметике, очистив ее от практических приложений, что впоследствии стало уделом "Логистики", которую греки не признавали настоящей наукой. Числа пифагорейцы мыслили зримо... Особенности языка математики Математика как язык науки Представляя собой тип формального знания, математика занимает особое место в отношении наук фактуального профиля. Она оказывается хорошо приспособленной для количественной обработки любой научной информации, независимо от ее содержания... Призма 1.2. О развитии геометрии в Древней Греции до Евклида Ученые и философы Древней Греции восприняли и переработали достижения культуры и науки Древнего Востока. Фалес, Пифагор, Демокрит, Евдокс и др. ездили в Египет и Вавилон для изучения музыки, математики и астрономии... Разрешение философских парадоксов в математике а) Математика в апориях Зенона Произведем вначале краткий исторический экскурс. Как известно, Зенон Элейский, будучи учеником Парменида, взял на себя задачу доказать, что проблема о едином бытии, поставленная его учителем, вовсе не абсурдна и не смехотворна... Расширение понятия числа 3.2.1. Отрицательные числа в Древней Азии Положительные количества в китайской математике называли «чен», отрицательные - «фу»; их изображали разными цветами: «чен» - красным, «фу» - черным. Такой способ изображения использовался в Китае до середины XII столетия... Философия математики 1. Греческая математика и её философия Философия впервые в истории человечества возникла в странах Древнего Востока - Египте, Вавилоне, Индии, Китае. Здесь же впервые зарождаются и системы математических знаний. Последние носили преимущественно характер эмпирических сведений... math.bobrodobro.ru Читать реферат по всему другому: "Математика в древней Индии" (Назад) (Cкачать работу) Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме! Реферат Математика в древней Индии Исполнитель:Цуй Александра Проверил:_________________________ _________________________ _________________________ Белгород 2005 В Индии математика зародилась примерно тогда же, когда и в Египте, – пять с лишним тысяч лет назад. К началу нашего летоисчисления индийцы уже были замечательными математиками. Кое в чем они обогнали даже древних греков. Однако Индия была оторвана от других стран, – на пути лежали тысячи километров расстояния и высокие горы. Индийские ученые сделали одно из важнейших в математике открытий. Они изобрели позиционную систему счисления – способ записи и чтения чисел. Чтобы назвать большое число, индийцам приходилось после каждой цифры произносить название разряда. Это было громоздко, неудобно, и индийцы стали поступать иначе. Например, число 278 396 читали так: два, семь, восемь, три, девять, шесть – сколько цифр – столько слов. А если в числе не было какого-нибудь разряда, как, например, в числах 206 или 7013, то вместо названия цифры говорили слово «пусто». Чтобы не получалось путаницы, при записи на месте «пустого» разряда ставили точку. Позднее вместо точки стали рисовать кружок, который на языке хинди назывался «сунья», что значит «пустое место». Арабские математики перевели это слово на свой язык. Вместо «сунья» они стали говорить «сифр», а это уже знакомое нам слово. Слово «цифра» по наследству от арабов досталось и нам. Генеалогия современных цифр. Древние индийцы с их высокой интеллектуальностью и склонностью к абстрактному мышлению, естественно, должны были занять ведущее положение в математике. Европа заимствовала начатки арифметики и алгебры у арабов (чем и обьясняется название - арабские цифры), а арабы, в свою очередь, заимствовали их у Индии. Поразительные успехи, достигнутые индийцами в математике, сейчас хорошо известны, и признано, что основы современной арифметики и алгебры были заложены еще в древней Индии. Примитивный метод использования абак и применение римских и подобных им цифр долгое время задерживал прогресс, пока, наконец, десять индийских цифр, включая знак нуль, не освободили человеческий разум от этих ограничений и не показали в новом свете значение чисел. Эти цифровые обозначения были единственными в своем роде и полностью отличались от всех иных обозначений, которые применялись в других странах. Сейчас они получили достаточно широкое распространение, и мы принимаем их как должное, однако в свое время они создали условия для революционного прогресса. Понадобилось много веков, чтобы эти цифровые обозначения пришли из Индии через Багдад в западный мир. Сто пятьдесят лет назад, во времена Наполеона, Лаплас писал: «Индия дала нам остроумный метод выражения всех чисел посредством десяти знаков, причем, кроме величины каждого знака, имеет значение и его расположение. Эта глубокая и важная мысль кажется нам настолько простой, что мы не замечаем ее истинных достоинств, но ведь сама ее простота и большая легкость, которую она придала всем вычислениям, делают нашу арифметику одним из самых полезных изобретений. Мы оценим все величие этого достижения, когда вспомним, что мимо него прошел даже гений Архимеда и Апполония, двух величайших людей древности.» (L. Hogben. Mathematics for the Million. London. 1942). Возникновение геометрии, арифметики и алгебры в Индии восходит к далеким временам. Прежде всего, существовала, вероятно, какого-то рода геометрическая алгебра, применявшаяся при начертании фигур для ведических алтарей. В древнейших книгах упоминается о геометрическом методе преобразования квадрата в прямоугольник по заданной стороне: ax = c. Геометрические фигуры до сих пор широко используются в индусских обрядах. Первые хорошо сохранившиеся индийские тексты в области точных наук - это "Сиддханты", часть которых, "Сурья", дошла до нас, вероятно, в достаточно точно соответствующей оригиналу (примерно между 300 и 400 годами н. э.) форме. В этих книгах содержится в основном астрономия, там обнаружены эпициклы и шестидесятичные дроби. Такие факты позволяют предположить наличие влияния греческой астрономии, относящегося, быть может, к эпохе "Алмагеста". Возможно, что они указывают на непосредственный контакт с вавилонской астрономией. Но, кроме этого, "Сиддханты" содержат многочисленные типично индийские особенности. "Сурья Сидд-ханта" содержит таблицу значений синуса (джия), а не хорд. Результаты, изложенные в "Сиддхантах", систематически разъяснялись и развивались в индийских математических школах, укоренившихся преимущественно в Уджджайне (Центральная Индия) и в Майсоре (Южная Индия) . Известны имена и книги отдельных индийских математиков, начиная с пятого столетия н. э.; некоторые книги доступны в английских переводах. Наиболее известными математиками Индии были Ариабхата (прозванный "первым", около 500 г.) и Брахмагупта (около 625 г.). Насколько они были знакомы с результатами греков, вавилонян и китайцев, можно только предполагать, но, во всяком случае, они проявляют значительную оригинальность. Для их работ характерны арифметико-алгебраические разделы. В их склонности к неопределенным уравнениям проявляется некоторое родство с Диофантом. Современником Брахмагупты был Бхаскара I, автор комментария к трактату Ариабхаты и астрономического сочинения "Маха-Бхаскария", содержащего математические разделы {неопределенные линейные уравнения, элементы тригонометрии и пр.). За этими учеными в ближайшие столетия последовали другие, работавшие в тех же областях; в трудах последних представлено астрономическое, частично арифметико-алгебраическое направление, они занимались также измерениями и тригонометрией. Ариабхата I имел для π значение 3,1416. Любимым предметом было нахождение рациональных треугольников и четырехугольников. Особенно успешно над этим работал Магавира из Майсорской школы (около 850 г.). Известны также трактаты Шридхары (IX - X вв.), Ариабхаты II (около950г.), Шрипати (XI в.) и др. Около 1150г. в Уджджайне, где работал Брахмагупта, жил и работал другой выдающийся математик, Бхаскара П. Первое общее решение неопределенного уравнения первой степени ах + bу = с (а, b, с - целые числа) встречается у Брахмагупты. Поэтому, строго говоря, нет оснований называть неопределенные линейные уравнения диофантовыми. Диофант допускал еще и дробные решения, индийские математики интересовались только целочисленными. Они пошли дальше Диофанта и в том отношении, что допускали отрицательные корни уравнений, хотя это в свою очередь, должно быть, соответствует более древней практике, сложившейся под влиянием вавилонской астрономии. Например, для уравнения х2 - 45х = 250 Бхаскара II находил решения х = 50 и х = -5, но относительно приемлемости отрицательного корня он высказывал известный скептицизм. Его "Лилавати" в течение столетий оставалась на Востоке образцовой книгой по арифметике и искусству измерений; император Акбар перевел ее на персидский язык (1587 г.), в 1816 г. она была издана в Калькутте и после этого многократно переиздавалась как учебник математики для религиозных школ. В древней Индии было найдено много ценнейших математических результатов; например, недавно стало известно, что ряды Грегори-Лейбница длябыли найдены уже при Нилаканте (ок. 1500 г.). Пальма первенства принадлежала Индии в области арифметики и алгебры. Изобретатель или изобретатели десятичной системы и знака нуль неизвестны. Первое известное нам употребление знака нуль мы находим в одной из священных книг, датируемой примерно 200 годом до н.э. Считается вероятным, что десятичная система счисления была изобретена в начале христианской эры. Нуль, называется «сунья», или - ничто, изображался вначале в виде точки, а позже в виде маленького кружка. Он считался таким же числом, как и все остальные. Профессор Холстед следующим образом подчеркивал важнейшее значение этого изобретения: «Значение введения знака нуль нельзя переоценить. Эта способность дать пустому ничто не только место, имя, образ, символ, но также и практическое значение типична для народа Индии, страны, из которой все это пришло. Это все равно, что создать из referat.co Реферат Математика в древней ИндииРеферат Математика в древней Индии Исполнитель: Цуй Александра Проверил:_________________________ _________________________ _________________________ Белгород 2005 
В Индии математика зародилась примерно тогда же, когда и в Египте, – пять с лишним тысяч лет назад. К началу нашего летоисчисления индийцы уже были замечательными математиками. Кое в чем они обогнали даже древних греков. Однако Индия была оторвана от других стран, – на пути лежали тысячи километров расстояния и высокие горы. Индийские ученые сделали одно из важнейших в математике открытий. Они изобрели позиционную систему счисления – способ записи и чтения чисел. Чтобы назвать большое число, индийцам приходилось после каждой цифры произносить название разряда. Это было громоздко, неудобно, и индийцы стали поступать иначе. Например, число 278 396 читали так: два, семь, восемь, три, девять, шесть – сколько цифр – столько слов. А если в числе не было какого-нибудь разряда, как, например, в числах 206 или 7013, то вместо названия цифры говорили слово «пусто». Чтобы не получалось путаницы, при записи на месте «пустого» разряда ставили точку. Позднее вместо точки стали рисовать кружок, который на языке хинди назывался «сунья», что значит «пустое место». Арабские математики перевели это слово на свой язык. Вместо «сунья» они стали говорить «сифр», а это уже знакомое нам слово. Слово «цифра» по наследству от арабов досталось и нам. Генеалогия современных цифр. 
Древние индийцы с их высокой интеллектуальностью и склонностью к абстрактному мышлению, естественно, должны были занять ведущее положение в математике. Европа заимствовала начатки арифметики и алгебры у арабов (чем и обьясняется название - арабские цифры), а арабы, в свою очередь, заимствовали их у Индии. Поразительные успехи, достигнутые индийцами в математике, сейчас хорошо известны, и признано, что основы современной арифметики и алгебры были заложены еще в древней Индии. Примитивный метод использования абак и применение римских и подобных им цифр долгое время задерживал прогресс, пока, наконец, десять индийских цифр, включая знак нуль, не освободили человеческий разум от этих ограничений и не показали в новом свете значение чисел. Эти цифровые обозначения были единственными в своем роде и полностью отличались от всех иных обозначений, которые применялись в других странах. Сейчас они получили достаточно широкое распространение, и мы принимаем их как должное, однако в свое время они создали условия для революционного прогресса. Понадобилось много веков, чтобы эти цифровые обозначения пришли из Индии через Багдад в западный мир. Сто пятьдесят лет назад, во времена Наполеона, Лаплас писал: «Индия дала нам остроумный метод выражения всех чисел посредством десяти знаков, причем, кроме величины каждого знака, имеет значение и его расположение. Эта глубокая и важная мысль кажется нам настолько простой, что мы не замечаем ее истинных достоинств, но ведь сама ее простота и большая легкость, которую она придала всем вычислениям, делают нашу арифметику одним из самых полезных изобретений. Мы оценим все величие этого достижения, когда вспомним, что мимо него прошел даже гений Архимеда и Апполония, двух величайших людей древности.» (L. Hogben. Mathematics for the Million. London. 1942). Возникновение геометрии, арифметики и алгебры в Индии восходит к далеким временам. Прежде всего, существовала, вероятно, какого-то рода геометрическая алгебра, применявшаяся при начертании фигур для ведических алтарей. В древнейших книгах упоминается о геометрическом методе преобразования квадрата в прямоугольник по заданной стороне: ax = c. Геометрические фигуры до сих пор широко используются в индусских обрядах. Первые хорошо сохранившиеся индийские тексты в области точных наук - это "Сиддханты", часть которых, "Сурья", дошла до нас, вероятно, в достаточно точно соответствующей оригиналу (примерно между 300 и 400 годами н. э.) форме. В этих книгах содержится в основном астрономия, там обнаружены эпициклы и шестидесятичные дроби. Такие факты позволяют предположить наличие влияния греческой астрономии, относящегося, быть может, к эпохе "Алмагеста". Возможно, что они указывают на непосредственный контакт с вавилонской астрономией. Но, кроме этого, "Сиддханты" содержат многочисленные типично индийские особенности. "Сурья Сидд-ханта" содержит таблицу значений синуса (джия), а не хорд. Результаты, изложенные в "Сиддхантах", систематически разъяснялись и развивались в индийских математических школах, укоренившихся преимущественно в Уджджайне (Центральная Индия) и в Майсоре (Южная Индия) . Известны имена и книги отдельных индийских математиков, начиная с пятого столетия н. э.; некоторые книги доступны в английских переводах. Наиболее известными математиками Индии были Ариабхата (прозванный "первым", около 500 г.) и Брахмагупта (около 625 г.). Насколько они были знакомы с результатами греков, вавилонян и китайцев, можно только предполагать, но, во всяком случае, они проявляют значительную оригинальность. Для их работ характерны арифметико-алгебраические разделы. В их склонности к неопределенным уравнениям проявляется некоторое родство с Диофантом. Современником Брахмагупты был Бхаскара I, автор комментария к трактату Ариабхаты и астрономического сочинения "Маха-Бхаскария", содержащего математические разделы {неопределенные линейные уравнения, элементы тригонометрии и пр.). За этими учеными в ближайшие столетия последовали другие, работавшие в тех же областях; в трудах последних представлено астрономическое, частично арифметико-алгебраическое направление, они занимались также измерениями и тригонометрией. Ариабхата I имел для π значение 3,1416. Любимым предметом было нахождение рациональных треугольников и четырехугольников. Особенно успешно над этим работал Магавира из Майсорской школы (около 850 г.). Известны также трактаты Шридхары (IX - X вв.), Ариабхаты II (около950г.), Шрипати (XI в.) и др. Около 1150г. в Уджджайне, где работал Брахмагупта, жил и работал другой выдающийся математик, Бхаскара П. Первое общее решение неопределенного уравнения первой степени ах + bу = с (а, b, с - целые числа) встречается у Брахмагупты. Поэтому, строго говоря, нет оснований называть неопределенные линейные уравнения диофантовыми. Диофант допускал еще и дробные решения, индийские математики интересовались только целочисленными. Они пошли дальше Диофанта и в том отношении, что допускали отрицательные корни уравнений, хотя это в свою очередь, должно быть, соответствует более древней практике, сложившейся под влиянием вавилонской астрономии. Например, для уравнения х2 - 45х = 250 Бхаскара II находил решения х = 50 и х = -5, но относительно приемлемости отрицательного корня он высказывал известный скептицизм. Его "Лилавати" в течение столетий оставалась на Востоке образцовой книгой по арифметике и искусству измерений; император Акбар перевел ее на персидский язык (1587 г.), в 1816 г. она была издана в Калькутте и после этого многократно переиздавалась как учебник математики для религиозных школ. В древней Индии было найдено много ценнейших математических результатов; например, недавно стало известно, что ряды Грегори-Лейбница для  были найдены уже при Нилаканте (ок. 1500 г.). были найдены уже при Нилаканте (ок. 1500 г.). Пальма первенства принадлежала Индии в области арифметики и алгебры. Изобретатель или изобретатели десятичной системы и знака нуль неизвестны. Первое известное нам употребление знака нуль мы находим в одной из священных книг, датируемой примерно 200 годом до н.э. Считается вероятным, что десятичная система счисления была изобретена в начале христианской эры. Нуль, называется «сунья», или - ничто, изображался вначале в виде точки, а позже в виде маленького кружка. Он считался таким же числом, как и все остальные. Профессор Холстед следующим образом подчеркивал важнейшее значение этого изобретения: «Значение введения знака нуль нельзя переоценить. Эта способность дать пустому ничто не только место, имя, образ, символ, но также и практическое значение типична для народа Индии, страны, из которой все это пришло. Это все равно, что создать из нирваны динамомашины. Ни одно математическое изобретение не имело такого значения для общего прогресса разума и могущества человечества». uchebana5.ru Математика в древней Индии - Рефераты для всехРеферат Математика в древней Индии Исполнитель: Цуй Александра Проверил:_________________________ _________________________ _________________________ Белгород 2005 В Индии математика зародилась примерно тогда же, когда и в Египте, – пять с лишним тысяч лет назад. К началу нашего летоисчисления индийцы уже были замечательными математиками. Кое в чем они обогнали даже древних греков. Однако Индия была оторвана от других стран, – на пути лежали тысячи километров расстояния и высокие горы. Индийские ученые сделали одно из важнейших в математике открытий. Они изобрели позиционную систему счисления – способ записи и чтения чисел. Чтобы назвать большое число, индийцам приходилось после каждой цифры произносить название разряда. Это было громоздко, неудобно, и индийцы стали поступать иначе. Например, число 278 396 читали так: два, семь, восемь, три, девять, шесть – сколько цифр – столько слов. А если в числе не было какого-нибудь разряда, как, например, в числах 206 или 7013, то вместо названия цифры говорили слово «пусто». Чтобы не получалось путаницы, при записи на месте «пустого» разряда ставили точку. Позднее вместо точки стали рисовать кружок, который на языке хинди назывался «сунья», что значит «пустое место». Арабские математики перевели это слово на свой язык. Вместо «сунья» они стали говорить «сифр», а это уже знакомое нам слово. Слово «цифра» по наследству от арабов досталось и нам. Генеалогия современных цифр. Древние индийцы с их высокой интеллектуальностью и склонностью к абстрактному мышлению, естественно, должны были занять ведущее положение в математике. Европа заимствовала начатки арифметики и алгебры у арабов (чем и обьясняется название - арабские цифры), а арабы, в свою очередь, заимствовали их у Индии. Поразительные успехи, достигнутые индийцами в математике, сейчас хорошо известны, и признано, что основы современной арифметики и алгебры были заложены еще в древней Индии. Примитивный метод использования абак и применение римских и подобных им цифр долгое время задерживал прогресс, пока, наконец, десять индийских цифр, включая знак нуль, не освободили человеческий разум от этих ограничений и не показали в новом свете значение чисел. Эти цифровые обозначения были единственными в своем роде и полностью отличались от всех иных обозначений, которые применялись в других странах. Сейчас они получили достаточно широкое распространение, и мы принимаем их как должное, однако в свое время они создали условия для революционного прогресса. Понадобилось много веков, чтобы эти цифровые обозначения пришли из Индии через Багдад в западный мир. Сто пятьдесят лет назад, во времена Наполеона, Лаплас писал: «Индия дала нам остроумный метод выражения всех чисел посредством десяти знаков, причем, кроме величины каждого знака, имеет значение и его расположение. Эта глубокая и важная мысль кажется нам настолько простой, что мы не замечаем ее истинных достоинств, но ведь сама ее простота и большая легкость, которую она придала всем вычислениям, делают нашу арифметику одним из самых полезных изобретений. Мы оценим все величие этого достижения, когда вспомним, что мимо него прошел даже гений Архимеда и Апполония, двух величайших людей древности.» (L. Hogben. Mathematics for the Million. London. 1942). Возникновение геометрии, арифметики и алгебры в Индии восходит к далеким временам. Прежде всего, существовала, вероятно, какого-то рода геометрическая алгебра, применявшаяся при начертании фигур для ведических алтарей. В древнейших книгах упоминается о геометрическом методе преобразования квадрата в прямоугольник по заданной стороне: ax = c. Геометрические фигуры до сих пор широко используются в индусских обрядах. Первые хорошо сохранившиеся индийские тексты в области точных наук - это "Сиддханты", часть которых, "Сурья", дошла до нас, вероятно, в достаточно точно соответствующей оригиналу (примерно между 300 и 400 годами н. э.) форме. В этих книгах содержится в основном астрономия, там обнаружены эпициклы и шестидесятичные дроби. Такие факты позволяют предположить наличие влияния греческой астрономии, относящегося, быть может, к эпохе "Алмагеста". Возможно, что они указывают на непосредственный контакт с вавилонской астрономией. Но, кроме этого, "Сиддханты" содержат многочисленные типично индийские особенности. "Сурья Сидд-ханта" содержит таблицу значений синуса (джия), а не хорд. Результаты, изложенные в "Сиддхантах", систематически разъяснялись и развивались в индийских математических школах, укоренившихся преимущественно в Уджджайне (Центральная Индия) и в Майсоре (Южная Индия) . Известны имена и книги отдельных индийских математиков, начиная с пятого столетия н. э.; некоторые книги доступны в английских переводах. Наиболее известными математиками Индии были Ариабхата (прозванный "первым", около 500 г.) и Брахмагупта (около 625 г.). Насколько они были знакомы с результатами греков, вавилонян и китайцев, можно только предполагать, но, во всяком случае, они проявляют значительную оригинальность. Для их работ характерны арифметико-алгебраические разделы. В их склонности к неопределенным уравнениям проявляется некоторое родство с Диофантом. Современником Брахмагупты был Бхаскара I, автор комментария к трактату Ариабхаты и астрономического сочинения "Маха-Бхаскария", содержащего математические разделы {неопределенные линейные уравнения, элементы тригонометрии и пр.). За этими учеными в ближайшие столетия последовали другие, работавшие в тех же областях; в трудах последних представлено астрономическое, частично арифметико-алгебраическое направление, они занимались также измерениями и тригонометрией. Ариабхата I имел для π значение 3,1416. Любимым предметом было нахождение рациональных треугольников и четырехугольников. Особенно успешно над этим работал Магавира из Майсорской школы (около 850 г.). Известны также трактаты Шридхары (IX - X вв.), Ариабхаты II (около950г.), Шрипати (XI в.) и др. Около 1150г. в Уджджайне, где работал Брахмагупта, жил и работал другой выдающийся математик, Бхаскара П. Первое общее решение неопределенного уравнения первой степени ах + bу = с(а, b, с- целые числа) встречается у Брахмагупты. Поэтому, строго говоря, нет оснований называть неопределенные линейные уравнения диофантовыми. Диофант допускал еще и дробные решения, индийские математики интересовались только целочисленными. Они пошли дальше Диофанта и в том отношении, что допускали отрицательные корни уравнений, хотя это в свою очередь, должно быть, соответствует более древней практике, сложившейся под влиянием вавилонской астрономии. Например, для уравнения х2 - 45х = 250 Бхаскара II находил решения х = 50 и х = -5, но относительно приемлемости отрицательного корня он высказывал известный скептицизм. Его "Лилавати" в течение столетий оставалась на Востоке образцовой книгой по арифметике и искусству измерений; император Акбар перевел ее на персидский язык (1587 г.), в 1816 г. она была издана в Калькутте и после этого многократно переиздавалась как учебник математики для религиозных школ. В древней Индии было найдено много ценнейших математических результатов; например, недавно стало известно, что ряды Грегори-Лейбница для были найдены уже при Нилаканте (ок. 1500 г.). Пальма первенства принадлежала Индии в области арифметики и алгебры. Изобретатель или изобретатели десятичной системы и знака нуль неизвестны. Первое известное нам употребление знака нуль мы находим в одной из священных книг, датируемой примерно 200 годом до н.э. Считается вероятным, что десятичная система счисления была изобретена в начале христианской эры. Нуль, называется «сунья», или - ничто, изображался вначале в виде точки, а позже в виде маленького кружка. Он считался таким же числом, как и все остальные. Профессор Холстед следующим образом подчеркивал важнейшее значение этого изобретения: «Значение введения знака нуль нельзя переоценить. Эта способность дать пустому ничто не только место, имя, образ, символ, но также и практическое значение типична для народа Индии, страны, из которой все это пришло. Это все равно, что создать из нирваны динамомашины. Ни одно математическое изобретение не имело такого значения для общего прогресса разума и могущества человечества». referat-4all.ru
|
