Презентация, доклад Система счисления древней Руси. Система счисления древней руси
Система счисления древней Руси - презентация, доклад, проект Обратная связь Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания: Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания: Email: [email protected] Мы в социальных сетях Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам ВКонтакте > Что такое Myslide.ru? Myslide.ru - это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями. Для правообладателей > myslide.ru ParaScience.info - Система счисления Древней Руси Славянские народы для записи чисел пользовались алфавитной нумерацией. В России славянская нумерация сохранилась до конца XVII в. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранилась только в богослужебных книгах. Изопсефи́я (абджадия в арабском языке, акшара-санкхья в деванагари, гематрия в иврите) - это один из методов анализа смысла слов и фраз на основе числовых значений входящих в них букв. Сумма числовых значений раскрывает символическую (скрытую) смысловую связь. 
 Числа от 1 до 9 изображались буквами славянского алфавита и что бы воспринимать букву как число, над ней писали специальный значок — титло.  Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком. Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.  Десятки обозначались так:  Сотни обозначались так:  Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве.  | 
| Тысяча | Тысячи записывались теми же буквами с титлом, но слева внизу изображалась наклонная линия, которая пересекалась двумя чёрточками. | 1000 | | 
| Тьма | Десятки тысяч назывались «тьмы», их обозначали, обводя знаки единиц кружками. Отсюда и произошло название «Тьма народу», т. е. очень много народу. | 10 000 | | 
| Легион | Сотни тысяч назывались «легионами», их обозначали, обводя знаки, единиц кружками из точек | 100 000 | | 
| Леодр | Миллионы назывались «леодрами». Их обозначали, обводя знаки единиц кружками из лучей или запятых. | 1 000 000 | | 
| Ворон | Десять миллионов в древнерусском счете именовались - ворон (вран).Воронов обозначали соответствующей буквой в кружке из крестиков. | 10 000 000 | | 
| Колода | Сотни миллионов назывались «колодами». «Колода» имела специальное обозначение - над буквой и под буквой ставились квадратные скобки. | 100 000 000 |

parascience.info Сайт по система счсиления - Славянская система счисления Славянская система счисления Более современными непозиционными системами счисления были алфавитные системы. К числу таких систем счисления относились славянская, ионийская (греческая), финикийская и другие. В них числа от 1 до 9, целые количества десятков (от 10 до 90) и целые количества сотен (от 100 до 900) обозначались буквами алфавита. Алфавитная система была принята в древней Руси. Числа от 1 до 10 записывались так: Над буквами, обозначавшими числа, ставился специальный знак – титло. Это делалось для того, чтобы отличить числа от обычных слов: 
Интересно, что числа от 11 (один – на десять) до 19 (девять – на десять) записывали так же, как говорили, то есть «цифру» единиц ставили до «цифры» десятков. Пример: Запишем в славянской записи числа 444 и 32: 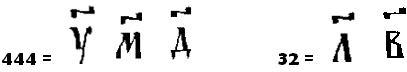
Мы видим, что запись получилась не длиннее нашей десятичной. Это объясняется тем, что в алфавитных системах использовались, по крайней мере, 27 «цифр». Но эти системы были удобны только для записи чисел до 1000. Правда, славяне, как греки, умели записывать числа и больше 1000. Для этого к алфавитной системе добавляли новые обозначения. Так, например, числа 1000, 2000… записывали теми же «цифрами», что и 1, 2, 3…, только перед «цифрами» ставили слева снизу специальный знак: 1000 = 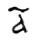 Число 10000 обозначалось той же буквой, что и 1, только без титла, ее обводили кружком: 10000 =  Называлось это число «тьмой». Отсюда и произошло выражение «тьма народу». Таким образом, для обозначения «тем» (множественное число от слова тьма) первые 9 «цифр» обводились кружками. 10 тем было единицей вышего разряда. Ее называли «легион». 10 легионов составляли «леодр». Самая большая из величин, имеющих свое обозначение, называлось «колода», она равнялась 1050. Такой способ записи чисел можно рассматривать как зачатки позиционной системы, так как в нем для обозначения единиц разных разрядов применялись одни и те же символы, к которым лишь добавлялись специальные знаки для определения значения разряда. Назад number-systems.3dn.ru Онлайн калькулятор: Древнерусская (византийская) система летосчисленияЕсть в хронологии такое понятие как эра. Дело в том, что каков бы ни был календарный год, он должен иметь порядковый номер, то есть отсчитываться от какой-либо начальной даты — основы летосчисления. Собственно, сам термин эра, как считается, это аббревиатура следующей фразы: «ab exordio regni Augusti», т. е. «от начала царствования Августа» (aera — эра). В связи с этим заметим, что эра может быть реальной — это когда счет лет идет от какого-либо реального события, например, от начала царствования, или фиктивной — это когда счет лет идет от какого-либо мифического события, например, от сотворения мира.До тех пор пока счет последователен, это не играет никакой роли. Одну такую эру мы знаем — христианскую эру, или систему летосчисления от Рождества Христова.Она была создана римским монахом Дионисием Малым в VI в. н. э. Тогда использовалась так называемая эра Диоклетиана, т. е. счёт лет вёлся от даты вступления на престол римского императора Диоклетиана.Дионисий каким-то образом рассчитал, что год рождения Христа имел место за 284 года до начала эры Диоклетиана, или, другими словами, приравнял начальный год царствования Диоклетиана к 284 г. христианской эры. Эра Дионисия была принята во всей христианской Европе. Совсем не так обстояло дело в России. Поскольку христианство пришло к нам из Византии, оттуда же пришла к нам и византийская система летосчисления от сотворения мира. Эта система использовалась в России вплоть до 1700 года, пока указом Петра I Россия не была переведена на христианскую эру. Согласно византийской системе летосчисления, от сотворения мира до рождества христова прошло 5508 лет. Год в ней, так же как и в христианской системе, был построен на базе юлианского календаря. Казалось бы, если разница только в точке отсчета, то перевод между эрами тривиален, но на самом деле в древней Руси до конца XVII века новый год начинался не с января, как в христианской эре, а с марта (как в древнем Риме) или с сентября (как в Византии). То есть, до указа Петра I существовало параллельно аж два календарных стиля: мартовский, согласно которому новый год приходился на 1 марта, и сентябрьский, с новым годом, наступающим 1 сентября. Разные стили немного меняют способ расчета, так как в мартовском стиле новый год отстает на два месяца от нового года христианской эры, а в сентябрьском стиле, наоборот, опережает новый год христианской эры на четыре месяца. Поясним это на примере. Предположим, указан март 7100 года по «мартовскому стилю». Это соответствует (7100-5508=1592) марту 1592 года от Рождества Христова.Если же указан февраль 7100 года по «мартовскому стилю», то есть практически конец года, то он будет соответствовать февралю 1593 года от Рождества Христова. Теперь рассмотрим сентябрь 7100 года по «сентябрьскому стилю». Это соответствует сентябрю 1591 года от Рождества Христова, а вот февраль 7100 года по «сентябрьскому стилю» соответствует февралю 1592 года. При этом при датировке событий в летописях, естественно, не указывалось, какой «стиль» используется. Впрочем, существует масса логических приемов, помогающих исследователям установить используемый в летописи стиль. Также известно, что с конца XV века сентябрьский стиль практически вытесняет мартовский (действительно, зачем равняться на Рим). К тому же у мартовского стиля было еще две модификации — ультра-мартовский и цирка-мартовский стили, но в такие дебри мы уже лезть не будем. Собственно, калькулятор ниже переводит даты из нашей эры в древнерусскую (византийскую), и служит больше для развлечения. Задача обратного перевода, нужная для правильной датировки летописей, как было показано выше, более сложна и требует анализа контекста для определения используемого в летописи стиля. Заключительное слово о месяцах — поскольку в основе лежал древнеримский (юлианский) календарь, то в наиболее ранних источниках названия месяцев встречаются в форме, наиболее близкой к латинскому прообразу, еще не приобретшие русифицированную форму, например, иуний, иулий, аугуст и так далее. Григорианская датаОбновление...Обновление...Обновление...ВекОбновление... Использовать ранние названия месяцевДревнерусская дата (мартовский стиль) Древнерусская дата (сентябрьский стиль) planetcalc.ru Системы счислений Из истории счета Люди научились считать еще в незапамятные времена. Сначала
они просто различали один предмет перед ними или нет. Если предмет был
не один, то говорили «много». Постепенно появилось слово для обозначения
двух предметов. Счет парами очень удобен. И не случайно у некоторых
племен Австралии и Полинезии до самого последнего времени было только
два числительных: «один» и «два». А все числа, большие двух, получали
названия в виде сочетаний этих двух числительных. Например, три -это
«один, два», четыре - «два, два», пять - «два, два, один». Наиболее
древней и простой «счетной машиной» издавна являются пальцы рук и ног.
И даже в наше время еще пользуются этим «счетным прибором», который
всегда при нас. На пальцах можно решать примеры не только в пределах
десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться
для счета пальцами как рук, так и ног. Таким образом они могли, казалось
бы, считать лишь до двадцати. Но с помощью этой «босоногой машины» люди
могли достигать значительно больших чисел, так как они фактически пользовались
двадцатеричной системой счисления: 1 человек - это 20, 2 человека -
это два раза по 20 и т.д. Записывали
числа поначалу совсем просто: делали зарубки на куске дерева или кости.
На этой кости тридцать тысяч лет назад сделаны нарезки,
они показывают, что уже тогда наши предки умели не только считать, но
и записывать результаты счета! Когда понадобилосьзаписывать большие числа, то для пятерок
и десяток стали придумывать новые знаки. Со временем потребовались знаки
для десятка десятков и так далее.Очень наглядной была система таких
знаков у египтян: Вот как египтяне записывали число 3 246: Запомнить большие числа трудно, поэтому к «счетной машине»
рук и ног добавляли механические приспособления. Например, перуанцы
употребляли для запоминания чисел разноцветные шнуры с завязанными на
них узлами. Веревочные счеты с узелками применялись и в России, и во
многих странах Европы. Остатками этого способа является практикуемое
еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками,
зернами, веревкой с узелками, другие - палочками с зарубками. Это были
первые счетные приборы, которые в конце концов привели к образованию
различных систем счисления. По
мере развития цивилизации потребность человека в счете стала просто
необходимой. Первона чально натуральные числа изображались с помощью
количества черточек или палочек. Затем для их изображения стали использовать
буквы или специальные знаки. Примером такой системы счисления является
пришедшая из Древнего Рима римская система,
в которой числа изображались буквами латинского алфавита. Римскими цифрами
иногда пользуются и сегодня: например, ими часто нумеруют главы в книгах.
Однако вычислять с помощью римских цифр так же неудобно, как и с помощью
египетских. Казалось бы, удобные цифры должны были изобрести древние
греки, которые создали математику как науку. Однако вычислениями греки
не увлекались и поэтому ограничились просто тем, что обозначили числа
буквами своего алфавита. Также, буквами, обозначались числа и в Древней
Руси Те очень удобные числа, которыми мы пользуемся сегодня,
изобрели индийцы: они так любили вычислять, что даже математические
книги писали в стихах! (Представляете себе, насколько легче было бы
выучить таблицу умножения, если бы она была записана стихами?) Индийцы
догадались, что значение цифры может зависеть от ее места в записи числа,
именно благодаря этому оказалось возможным записывать все числа с помощью
всего десяти цифр. Индийские цифры так сильно упростили вычисления, что со
временем завоевали весь мир. В Европу эти цифры попали благодаря арабам,
поэтому индийские цифры называют арабскими. До этого в Европе пользовались римскими цифрами. О том,
насколько трудны были вычисления с этими цифрами, говорят слова одного
европейского ученого, который жил около 700 года: “В мире есть много
трудных вещей, но нет ничего труднее четырех действий арифметики!” Л.
Генденштейн Существовали
системы исчисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная
система счисления. Остатки ее мы находим в сохранившемся до сих пор
делении часа или градуса на 60 минут, а минуты - на 60 секунд. Широкое
распространение имела в древности и двенадцатеричная система, происхождение
которой, вероятно, связано, как и десятичной системы, со счетом на пальцах:
за единицу счета принимались фаланги (отдельные суставы) четырех пальцев
одной руки, которые при счете перебирались большим пальцем той же руки.
Остатки этой системы счисления сохранились и до наших дней и в устной
речи, и в обычаях. Хорошо известно, например, название единицы второго
разряда - числа 12 - "дюжина". Сохранился обычай считать многие
предметы не десятками а дюжинами, например столовые приборы в сервизе
или стулья в мебельном гарнитуре
Самой молодой системой счисления по праву можно считать двоичную. Эта
система обладает рядом качеств, делающей ее очень выгодной для использования
в вычислительных машинах и в современных компьютерах. Официальное рождение двоичной арифметики связанно с именем
Г.В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел
правила выполнения арифметических действий над двоичными числами.
Двоичная система проста, так как для представления информации в ней
используются всего два состояния или две цифры. Такое представление
информации принято называть двоичным кодированием. Представление информации
в двоичной системе использовалось человеком с давних времен. Так, жители
островов Полинезии передавали необходимую информацию при помощи барабанов:
чередование звонких и глухих ударов. Звук над поверхностью воды распространялся
на достаточно большое расстояние, таким образом "работал"
полинезийский телеграф. В телеграфе в Х1Х-ХХ веках информация передавалась
с помощью азбуки Морзе - в виде последовательности из точек и тире.
Часто мы договариваемся открывать входную дверь только по "условному
сигналу" - комбинации коротких и длинных звонков. Двоичная система
используется для решения головоломок и построения выигрышных стратегий
в некоторых играх. irnik.narod.ru История числа в древней руси. Система счисления древней руси Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначались буквами с особым знаком « » (титло), который писали над буквой. Первые 10 букв обозначали единицы, следующие 10 букв - десятки, а последние 9 букв - сотни. Число 10000 называли словом «тьма». Современная достаточно простая десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы назвали «арабскими», а арабы «индийскими». Эта система была введена в Европе примерно в 1120 году английским учёным путешественником Аделардоли. К 1600 году она была принята в большинстве стран мира. Много есть разных версий об истории возникновения цифр. Всем нашим выступающим сегодня цифрам нравится версия Пушкина. Пушкин считал, что все арабские цифры произошли из магического квадрата. Наряду с развитием науки о числах появились и различные числовые суеверия. Пифагорейцы, изучая окружающую природу, пришли к идее, каждому явлению природы, каждой вещи поставить в соответствии число. Ученики Пифагора нашли соотношение между длинами сторон и музыкальными тонами. Укорачивание струн в отношении 2: 1; 3: 2; 4: 3 давало известные в музыке интервалы: октаву, квинту, кварту. Даже каждого человека можно закодировать числом. За каждым числом прячется тайна. Например, одно из обозначений букв цифрами: A - 1 Б - 2 В - 6 Г - 3 Д - 4 Е - 5 Ж - 2 З - 7 И - 1 К - 2 Л - 2 М - 4 О - 7 П - 8 Р - 2 С - 3 Т - 4 У - 6 Ф - 8 Х - 5 Ц - 3 Ч - 7 Ш - 2 Щ - 9 Ы - 1 Ь - 1 Э - 6 Ю - 7 Я - 2 Все однозначные числа - главные. Цифра 1 или число 1 - самое главное число. Есть тому доказательства. Любое натуральное число можно представить в виде предшествующего числа и единицы, например: 2 = 1 + 1; 3 = 2 + 1; 4 = 3 + 1 и так далее. Единица не изменяется при возведении её в любую степень. Единицу можно представить через все 10 цифр. 1 = 2/2; 1= 3-2; 1= 4/4 и т.д. В древности заключили: без единицы нет никакого числа, все числа получаются из единицы; никакое число не может быть представлено без единицы; законы чисел и их порядок выведены из единицы. Цифра 2 или число 2 тоже самое главное число. Есть веские доказательства. С помощью 5 двоек и знаков можно представить любое число от 1 до 9. 1 = 2/2; 3 = 2 + 2/2; 4 = 2 + 2 и т.д. Число 3 в древности считалось числом совершенства, так как это число равное сумме предыдущих ему чисел в натуральном ряду. 3 = 1 + 2; С помощью 4 троек можно записать все числа от 1 до 10. 1 = 3/3; 2 = 3 - 3/3; 4 = 3 + 3/3 и т.д. Много интересных свойств чисел найдено учёными математиками Леонардом Эйлером и И.М. Виноградовым. Служители решили считать число 3 священным признаком совершенства. А число 4 мистики признали числом силы, так как они заметили, что из суммы 4 чисел непосредственно получаются все числа первого десятка. Платон считал основой мира математический знак и все свойства окружающего мира выводил из свойств геометрических форм: 4 главных стихии - вода, воздух, земля и огонь. Число 5, умноженное само на себя, даёт на последнем месте самого себя, поэтому в древности число 5 называли круговым числом, и считали его символом течения времени. Египтяне заметили, что квадрат числа 5 равен сумме квадратов чисел: 25 =16+9. Правильный звёздчатый пятиугольник пифагорейцы считали за символ здоровья, эта фигура была эмблемой их союза: Если 6 умножают само на себя, то на последнем месте получают 6, поэтому в древности его тоже называли круговым числом или символом течения времени. Число 7 приобрело ореол святости в древности, когда, кроме ранее открытых 3 небесных тел - Солнца, Луны и Венеры, были открыты ещё Марс, Меркурий, Юпитер и Сатурн. В большинстве поговорок о «семи» семь означает много. Вы узнали много интересного о числах, но ни одно из этих чисел не обладает теми свойствами, которыми обладает 8. Если число 8 будем умножать на число натурального ряда от 1 до 5, то получим в произведении такие числа, сумма цифр которых будет уменьшаться. 1х 8 = 8; Пифагор и его ученики наблюдали за свойствами числа 8, называли его символом смерти, так как сумма цифр чисел, кратных восьми, уменьшаются. Если умножить все числа от 1 до 10 на 9 всегда получим число, сумма цифр которого есть 9. Впоследствии этого свойства пифагорейцы число 9 назвали символом постоянства. - 1 - божественное число
- 2 - духочуст
mobiwar.ru
|
