Пропорции в египетской архитектуре - История архитектуры. Пропорции древнего египта

Пропорции в египетской архитектуре - История архитектуры

Главное меню:

• Всеобщая история архитектуры
• Первобытнообщинный период
• Первобытнообщинный период
• Рабовладельческое общество
• Рабовладельческое общество
  • Карта раздела «Рабовладельческое общество»
  • Рабовладельческое общество
  • Древний Египет
  • Эфиопия
  • Эгейский мир
  • Двуречье и Месопотамия
  • Передняя Азия
  • Закавказье
  • Иран
    • Иран
    • Иран. Мидия. Экбатаны. Гробницы
    • Иран. Гробницы Дукан-и-Дауд, Кызкапан и Курх-у-Кич
    • Иран. Ахеменидский период. Сузы, Персеполь
    • Иран. Пасаргады. Дворцы
    • Иран. Персеполь. Дворцы
    • Иран. Персеполь. Дворец Ксеркса
    • Иран. Дворцы Дария
    • Иран. Сузы. Дворец Дария
    • Иран. Гробницы Кира, Дария, Да-у-Духтар
    • Иран. Святилища
    • Иран. Эпоха Ахеменидов. Этапы развития архитектуры
    • Парфия
    • Парфия. Селевкия, Ктесифон
    • Парфия. Хатра
    • Парфия. Ашшур, Дура-Европос
    • Парфия. Жилые дома
    • Парфия. Дворец Хатры
    • Парфия. Дворцы Ашшура, Ниппура, Кухи-Ходжа
    • Парфия. Культовые сооружения
    • Парфия. Фортификация
    • Парфия. Гробницы
    • Парфия. Общественная архитектура
    • Иран. Сасанидское государство
    • Иран. Гур, Дарабгерда, Бишапур, Нишапур
    • Иран. Ктесифон. Фортификация городов
    • Иран. Арки, своды, купола
    • Иран. Арки, своды, купола 2
    • Иран. Дари-Шахр, Ширван, Тель-Дехаб
    • Иран. Дворец в Фирузабаде, ансамбль Бишапура
    • Иран. Дворец в Сарвистане, дворец в Ктесифоне — Таки-Кисра
    • Иран. Дворец Касри-Ширин, комплекс Хош-Кури
    • Иран. Парковые гроты Таки-Бустана
    • Иран сасанидский. Культ огня. Чортак
    • Иран сасанидский. Христианство. Культовые алтари
    • Иран. Особенности общественного строительства
    • Иран. Искусство
    • Иран. Искусство 2
  • Средняя Азия
  • Афганистан
  • Юго-Восточная Азия
  • Дальний Восток. Китай
  • Дальний Восток. Корея
  • Дальний Восток. Япония
  • Америка. Этапы развития
• Архитектура античного мира
• Архитектура античного мира
  • Карта раздела «Архитектура античного мира»
  • Архитектура античного мира
  • Архитектура древней Греции
  • Греция. Архитектура древнейшей эпохи (XII - середина VIII в. до н.э.)
  • Греция. Архитектура архаической эпохи (750-480 гг. до н.э.)
  • Архитектура греческой метрополии
  • Архитектура Великой Греции
  • Архитектура Малой Азии и островов Эгейского моря
  • Греция. Архитектура эпохи расцвета (480-400 гг. до н.э.)
  • Сооружения второй четверти V в. до н.э. вне Афин
  • Расцвет аттической архитектуры
  • Сооружения 2-й половины V в. до н.э. в Великой Греции и Малой Азии
  • Греция. Архитектура IV в. до н.э. (400—323 гг. до н.э.)
  • Греция. Архитектура эпохи эллинизма (323г. до н.э.-Iв. н.э.)
  • Греция Эллинизм. Общественные сооружения
  • Греция. Эллинизм. Культовое строительство
  • Греция. Эллинизм. Мемориальные сооружения
  • Архитектура античных государств Северного Причерноморья
  • Вклад древней Греции в мировое развитие архитектуры
  • Архитектура древнего Рима
  • Этрусская архитектура
  • Архитектура Римской республики
  • Римская республика. Общественные сооружения
  • Римская республика. Инженерные сооружения
  • Римская республика. Жилые сооружения
  • Римская республика. Виллы
  • Архитектура Римской империи
  • Римская империя. Градостроительство
  • Римская империя. Общественные сооружения
  • Римская империя. Мемориальные и триумфальные сооружения
  • Римская империя. Инженерные сооружения
  • Римская империя. Жилые сооружения
  • Римская империя. Погребальные сооружения
  • Ордер
  • Декор
  • Декор 2
  • Композиция
  • Роль римской архитектуры
  • Раннехристианская архитектура
• Архитектура Восточной Европы. Средние века
• Архитектура Восточной Европы. Средние века
  • Карта раздела «Архитектура Восточной Европы. Средние века»
  • Архитектура Восточной Европы. Средние века
  • Архитектура Восточной Европы. Средние века 2
  • Архитектура Восточной Европы. Средние века 3
  • Архитектура Восточной Европы. Средние века 4
  • Архитектура Восточной Европы. Средние века 5
  • Архитектура Византии
  • Архитектура Армении
    • Архитектура Армении
    • Архитектура IV—VII вв.
    • Архитектура IX-XI вв.
      • Развитие Армении политическое IX—XI вв
      • Развитие Армении экономическое IX—XI вв
      • Ани, Лори-берд
      • Амберд, Бджни, Каянберд, Тигнис, Магасберд, дворец Багратидов
      • Айраванка, Нарекаванка, Ованнеса, храм Креста, собор Аракелоц
      • Ани. Кафедральный собор, Гагикашен, церкви Григория Абугамренц и Спасителя
      • "Пастушья" церковь, Аракелоц, Аменапркич, Ншана
      • Храм в Мармашене, Гавиты, Татев, Хцконк, хачкар, Гавазан
    • Архитектура XII—XIV вв.
    • Архитектура киликийской Армении (1080—1375 гг.)
    • Архитектура XV—XIX вв.
    • Роль архитектуры феодальной Армении
  • Архитектура Грузии
    • Архитектура древнего времени ( IV—VII вв.)
    • Архитектура VIII—IX вв.
    • Архитектура X—XI вв.
    • Архитектура XII—XIII вв.
    • Архитектура XIII—XV вв.
    • Архитектура XVI—XVIII вв.
  • Архитектура Болгарии
  • Архитектура Сербии и Македонии
    • Сербия и Македония. Особенности развития
    • Сербия и Македония. Особенности развития 2
    • Градостроительство. Крепости, замки, монастыри
    • Градостроительство. Замки, монастыри, жилые дома
    • Культовая архитектура раннефеодального периода
    • Период господства Византии
    • Рашская архитектурная школа
    • Рашская архитектурная школа. Храмы. Тип, материалы
    • Рашская архитектурная школа. Храмы. Интерьеры. Пропорции. Декор
    • Македонская и косовско-метохийская школа. Храмы. Формы, планы, особенности
    • Македонская и косовско-метохийская школа. Храмы. Формы, декор
    • Моравская школа. Храмы. Форма, особенности
    • Моравская школа. Храмы. Форма, материал, декор
    • Моравская школа. Храмы. Декор. Фрески
    • Роль архитектуры Сербии и Македонии
  • Архитектура Молдавии и Валахии

archisto.info

«Пропорции в архитектуре Древнего Египта»

«Пропорции в архитектуре Древнего Египта» - страница №1/1

Цель проекта: Рассмотреть архитектурные памятники Древнего Египта, выявить особенность в архитектурных сооружениях древних египтян, связь математики и архитектуры.

Участники проекта: Учащиеся 10 класса.

Вступительное слово учителя:

Земля Египта всегда манила путешественников своими ни с чем несравнимыми памятниками искусства. Еще в V веке до н.э. древнегреческий историк Геродот описал впечатления от увиденного там, а философ Платон, высоко ценивший египетское искусство, ставил его в пример своим соотечественникам. И сегодня не ослабевает интерес к Египту. 

Искусство древних египтян многогранно: оно представлено архитектурными, скульптурными, живописными творениями, литературными памятниками.

Выдающимися архитектурными постройками Египта, конечно, являются пирамиды. Они являются сосредоточением достижений древнегреческой науки в области строительной техники и архитектуры, математики и астрономии, мифологии и религии.  В пригороде Каира – Гизе – находятся 3 крупнейших пирамиды Египта – фараона Хеопса, Хафра, Менкаура, отнесенные греками к 7 чудесам света. Всего в Египте насчитывается более 89 пирамид. Самые грандиозные из них – пирамида Хеопса, она сложена из 2.300.000 камней, массой около 2, 5 т. Каждый. До сих пор остается не вполне ясным, как многотонные камни поднимали на такую высоту, а также то, как были пригнаны камни друг к другу, если между ними нельзя просунуть лезвие ножа. Пирамида считалась домом умершего фараона, а форма означала вечность, а отношение граней – Божественную Гармонию Вселенной. 

Кроме пирамид в Древнем Египте строились заупокойные храмы в честь богов. Наиболее распространены были храмы-святилища в честь особо почитаемого бога Амона-Ра. Наиболее примечателен сложный архитектурный комплекс в Карнаке и Луксоре, который был возведён по обеим сторонам Нила недалеко от города Фивы. Этот грандиозный ансамбль строился на протяжении нескольких столетий. 

Великолепен и грандиозен храм Амона-Ра в Луксоре, главным украшением которого была колоннада длиной 260 метров. Перед его фасадом стояли два обелиска и шесть огромных статуй фараона.  Главное святилище посвящено богу Амону-Ра. Этот ансамбль состоит более чем их сотни обширных помещений, огромных дворов, бесчисленных аллей, переходов, колоссальных размеров статуй богов и фараонов, сфинксов и обелисков. 

Архитектура Древнего Египта – это архитектура пальм, сикомор и тростников. Египет – страна песков, основным строительным материалом служила илистая земля. Как же в таких условиях рабы построили могущественные сооружения – храмы и гробницы, которые поражают нас сегодня своими математически выверенными пропорциями?

Основополагающий вопрос: Каковы пропорции архитектурных сооружений Древнего Египта?

Вопросы для изучения:

1. В чем особенность архитектурных сооружений Древнего Египта?
2. Каковы особенности пропорций храмовых комплексов и гробниц?
3. Какова связь математики и архитектуры у древних египтян?

1 группа:

С точки зрения строительных приемов египетское искусство чрезвычайно просто. Глина позволяла возводить прочные своды без сложных лесов и кружал. Камень использовали в архитектуре Египта для возведения стен и столбов.  Храмы Египта строились как дольмены. Ни изысканной конструкции, ни беспокойных форм: горизонталь доминирует в композиции в композиции постройки и в окружающем пейзаже. Все устойчиво и долговечно. Такое грандиозное ощущение - таки простыми средствами.

На больших стройках, где работы велись сразу в нескольких пунктах, во избежание ошибок пользовались шнуром. Строились пирамиды методом последовательной кладки. С первых же лет своего правления фараон приступал к сооружению подземелья-крипты и ядра пирамиды. На протяжении всей своей жизни он продолжал постройку пирамиды и сооружал вторую погребальную камеру, которая была пышнее первой.

Пирамиды различают:

Наружные плоскости пирамид ориентированы по сторонам света. Пирамиды имеют погребальные камеры и вентилляционные шахты-каналы. 

Пирамида — это не только символом долговечности и абсолютного покоя, и служит не только усыпальницей. Многие ученые пришли к выводу, что в связи с необычайно четкой ориентацией Большой пирамиды и тем, что направление ее главной галереи совпадает с земной осью - пирамида еще, и астрономический памятник.

Щековая стена Египетских пирамид представляет собой лестницу, ступени которой служат для подноски материалов. Те ряды, по которым поднимались подносчики, выложены кирпичем положенным на ребро. Ряды кирпича идут волнистой линией. Они поднимаются и опускаются снова. Такое волнистое направление рядов объясняется употреблением шнура вместо правила (рейки). Шнур провисал и ряды становились волнистыми.

В архитектуре древнего Египта имели место и своды и купола.

Своды возводили из кирпича. История сводов в древности является историей тех приемов, при помощи которых было возможно возводить своды непосредственно над пролетами. 

Обычной формой египетских сводов является купол. Из всех древних типов свода сферический свод-купол легче всего возводится без кружал. Каждый ряд так незначительно свешивается над лежащим ниже его, что может удержаться без кружал. Как только кольцо сведено, оно уже не изменяет своей сферической формы и достаточно прочно, чтобы снести последующие ряды. Кладка исполняется тем легче, чем незначительнее свешивается внутрь одно кольцо над другим.

Египетские песчаники и известняки легко поддавались обработке. Кроме железных орудий египтяне пользовались распиловкой при помощи мокрого песка. Пилу заменяли железным лезвием или проволокой, дощечкой или веревкой. Передвигали камни при помощи салазок, их изображения сохранились на стенах каменоломни в Эль-Мазаре. Благодаря остроумному расположению канатов, камень, влекомый быками без особых приспособлений устанавливался с земли на полозья.

Обелиски создавались из глыб каменоломней Асуана. Их обрабатывали при помощи бронзовых клиньев, загнанных в борозды, заранее проведенные в гранитной скале. О перевозке обелисков писал еще Плиний: чтобы поднять обелиск его помещали между 2мя барками и с наступлением половодья Нила выводили из каменоломни.

Лотосообразные гаторические колонны в Египте, наряду с квадратными и многогранными столбами использовались также, как и круглые колонны. Стволу колонны придавали форму стебля, капители - форму цветка. Возможно, что прототипом такой лотосообразной колонны послужил декоративный мотив связки стеблей водяных растений на столбах хижин. В качестве декорирования помещений в архитектуре древнего Египта активно применялись металлические украшения.

Храмы древнего Египта — это обычно: святилище, как самая удаленная часть храма, предназначенная для пребывания божества; вокруг святилища — помещения служебного характера; перед святилищем — зал наос, доступный только для посвященных; перед наосом — обширный двор, куда допускались молящиеся.

Жилища в архитектуре древнего Египта: План египетского дома похож на план всякого азиатского жилища. Это всегда замкнутое помещение, с фасадом без окон, освещаемое только со стороны внутреннего двора; на крыше устроена терраса, где обитатели дома ночуют в жаркое время.

Зодчими в Египте становились, как правило, по наследству: от отца к сыну. Удавалось установить целые родословные архитекторов. Клейма фараонов на кирпиче встречаются даже в частных постройках.

Когда народы Европы были еще в полуварварском состоянии, в Египте уже существовали вполне развитые искусство и промышленность.

2 группа:

Архитектура Древнего Египта теснейшим образом связано с заупокойным культом. Классическим образцом архитектурных сооружений являются пирамиды фараонов 4 - й династии (27 в. до н.э.) Хеопса, Хефрена и Микерина. Их отточенная форма, основанная на пропорциях золотого сечения, была предельно лаконична и бесконечно выразительна. Два элемента определяли закономерности формы: основание, квадратное в плане, и схождение сторон в одной точке, подобно тому, как вся египетская жизнь сходилась, сфокусировалась в обожествленном фараоне. Гениальная в своей простоте пирамидальная конструкция несла художественное обобщение самой сути египетского общества, подчиненного безграничной власти фараона.

Характерной особенностью пирамид как архитектурных соображений было отношение массы и пространства: погребальная камера, где стоял саркофаг с мумией, очень небольшая, а подводили к ней длинные и узкие коридоры. Пространственный элемент был сведен к минимуму. Безраздельно господствовала масса всей пирамиды, в то время как сама пирамида была завершающей частью огромного пространственного ансамбля: на берегу Нила стоял небольшой нижний заупокойный храмик, от которого шел длинный крытый коридор. Поднимаясь по склону Ливийского плоскогорья, он подводил к верхнему заупокойному храму, расположенному у подножия пирамиды.

Пропорции в зданиях и частях зданий архитектуры Египта устанавливали между их размерами самые простые отношения 1:2, 3:5. 

Общая высота здания делилась обычно на три равные части: • Цоколь; • Ствол колонны; • и верхнюю часть здания до основания капители.

Последняя часть делится, в свою очередь, также на три части: 

Прием ритмических повторений: анфилады колонн, сдвоенные ряды сфинксов, повторяемость геометрии в статуях усиливают впечатление архитектурного комплекса.

Система пропорций, применявшаяся в архитектуре Древнего Египта, построена на квадрате и его производных. Эту систему построения ряда последовательно увеличивающихся производных квадрата мы будем называть в дальнейшем системой диагоналей.

3 группа:

В основе пропорций древнеегипетских храмов лежит золотое сечение. В построении пропорций возможны два основных метода.

1. Арифметические системы, где пропорции вычисляются абстрактным методом (по числам). Разновидностью этого способа является модульная система, при которой размер какой-либо части здания (например, диаметр колонны) принимается за единицу (модуль) и по отношению к нему все остальные размеры выражаются в простых числах.

2. Геометрические системы пропорций, где все три проекции сооружения определяются путем геометрических построений (чаще всего на основе квадрата или круга).

Наибольшую роль здесь играет принцип подобия частей.

Частным случаем геометрических построений является группа отношений так называемого «золотого сечения» (т. е. деления отрезка в среднем и крайнем отношении), при котором весь отрезок так относится к большей своей части, как большая часть относится к меньшей. Таким образом, постоянная пропорция этой системы, образуя убывающую или возрастающую прогрессию, связывает воедино все элементы здания, от больших до самых малых величин.

Золотым сечением наиболее часто занимались теоретики, исходя из квадрата, точнее из двух квадратов (Хембидж), или из деления окружности на 10 частей (Мёссель).

Оба названных исследователя приводят, кроме того, общие законы построений, объясняющие все схемы геометрических пропорций. Мёссель, например, выводит все геометрические фигуры из деления окружности на различное число частей. По Мёсселю пропорции храма Хонсу в Карнаке были определены путем вписывания его в круг (описанный веревкой на земле), разделенный на восемь частей (рис.).

Система пропорций, применявшаяся в архитектуре Древнего Египта, построена на квадрате и его производных (рис.). Эту систему построения ряда последовательно увеличивающихся производных квадрата мы будем называть в дальнейшем системой диагоналей.

Эти четыре фигуры, связанные между собой общим построением, обладают интересными свойствами.

Первая фигура — квадрат — одна из простейших фигур, имеющая равные стороны. Она является основной формой в ранней архитектуре Древнего Египта, также как и связанная с ней вторая фигура — прямоугольник с отношением сторон, равным отношению стороны квадрата к его диагонали (рис.).

Отношение сторон в нем √3/2=1,4142 или 1/√2=0,7071

Третья фигура (рис.) имеет отношение сторон 1/√3=1,7321

Половина этого прямоугольника образует прямоугольный треугольник с меньшей стороной, равной половине гипотенузы, и с углами 30° и 60°. Хорошо знакомый всем угольник с такими углами является, вероятно, самым ранним вспомогательным прибором в работе архитектора, наравне с угольником, имеющим угол 45° и равным половине квадрата.

Отношение большего катета к гипотенузе в треугольнике с углом 60° равно √3/2=0,866

Четвертая фигура представляет собой прямоугольник, составленный из двух квадратов (рис.)

В нем примечательно часто встречающееся в Египте отношение диагонали к большей стороне √5/2=1,1185, совпадающее с «функцией» золотого сечения. Отношение малого катета к диагонали 1/√5=0.4472.

Эти шесть связанных между собой величин:

1) квадрат;

2) его диагональ;

3) прямоугольный треугольник с углом 60°;

4) прямоугольник, состоящий из двух квадратов;

5) и 6) отношения его диагонали к сторонам √5/2 и 1/√5 лежат в основе пропорций большинства сооружений Древнего царства.

Иногда кроме квадрата применялся равносторонний треугольник (рис.). Он имеет уже знакомое отношение высоты к стороне √3/2:1= 0.866 или стороны к высоте 1: √3/2=1.155.

Все эти фигуры могут быть построены в натуре при помощи простой веревки. Даже прямоугольник с таким иррациональным и, казалось бы, сложным отношением сторон, как √5/2=1,118, которое является отношением диагонали двух квадратов к стороне (рис.), может быть построен этим простейшим способом (такой прямоугольник условно называется в дальнейшем неточным квадратом).

Это же отношение может быть получено при помощи диагонали полуквадрата (рис.), так как половина квадрата составляет прямоугольник в два малых квадрата.

В нем примечательно часто встречающееся в Египте отношение диагонали к большей стороне√5/2=1,11805, совпадающее с «функцией» золотого сечения. Отношение малого катета к диагонали 1/√5=0.4472.

Таким образом, в основе пропорций имеется связь математики и архитектуры, которая является золотым сечением.

Учащиеся, работавшие в группах, создали презентации, которые в дальнейшем объединили в одну.

umotnas.ru

«Пропорции в архитектуре Древнего Египта»

Цель проекта: Рассмотреть архитектурные памятники Древнего Египта, выявить особенность в архитектурных сооружениях древних египтян, связь математики и архитектуры.

Участники проекта: Учащиеся 10 класса.

Вступительное слово учителя:

Земля Египта всегда манила путешественников своими ни с чем несравнимыми памятниками искусства. Еще в V веке до н.э. древнегреческий историк Геродот описал впечатления от увиденного там, а философ Платон, высоко ценивший египетское искусство, ставил его в пример своим соотечественникам. И сегодня не ослабевает интерес к Египту. 

Искусство древних египтян многогранно: оно представлено архитектурными, скульптурными, живописными творениями, литературными памятниками.

Выдающимися архитектурными постройками Египта, конечно, являются пирамиды. Они являются сосредоточением достижений древнегреческой науки в области строительной техники и архитектуры, математики и астрономии, мифологии и религии.  В пригороде Каира – Гизе – находятся 3 крупнейших пирамиды Египта – фараона Хеопса, Хафра, Менкаура, отнесенные греками к 7 чудесам света. Всего в Египте насчитывается более 89 пирамид. Самые грандиозные из них – пирамида Хеопса, она сложена из 2.300.000 камней, массой около 2, 5 т. Каждый. До сих пор остается не вполне ясным, как многотонные камни поднимали на такую высоту, а также то, как были пригнаны камни друг к другу, если между ними нельзя просунуть лезвие ножа. Пирамида считалась домом умершего фараона, а форма означала вечность, а отношение граней – Божественную Гармонию Вселенной. 

Кроме пирамид в Древнем Египте строились заупокойные храмы в честь богов. Наиболее распространены были храмы-святилища в честь особо почитаемого бога Амона-Ра. Наиболее примечателен сложный архитектурный комплекс в Карнаке и Луксоре, который был возведён по обеим сторонам Нила недалеко от города Фивы. Этот грандиозный ансамбль строился на протяжении нескольких столетий. 

Великолепен и грандиозен храм Амона-Ра в Луксоре, главным украшением которого была колоннада длиной 260 метров. Перед его фасадом стояли два обелиска и шесть огромных статуй фараона.  Главное святилище посвящено богу Амону-Ра. Этот ансамбль состоит более чем их сотни обширных помещений, огромных дворов, бесчисленных аллей, переходов, колоссальных размеров статуй богов и фараонов, сфинксов и обелисков. 

Архитектура Древнего Египта – это архитектура пальм, сикомор и тростников. Египет – страна песков, основным строительным материалом служила илистая земля. Как же в таких условиях рабы построили могущественные сооружения – храмы и гробницы, которые поражают нас сегодня своими математически выверенными пропорциями?

Основополагающий вопрос: Каковы пропорции архитектурных сооружений Древнего Египта?

Вопросы для изучения:

1. В чем особенность архитектурных сооружений Древнего Египта?
2. Каковы особенности пропорций храмовых комплексов и гробниц?
3. Какова связь математики и архитектуры у древних египтян?

1 группа:

С точки зрения строительных приемов египетское искусство чрезвычайно просто. Глина позволяла возводить прочные своды без сложных лесов и кружал. Камень использовали в архитектуре Египта для возведения стен и столбов.  Храмы Египта строились как дольмены. Ни изысканной конструкции, ни беспокойных форм: горизонталь доминирует в композиции в композиции постройки и в окружающем пейзаже. Все устойчиво и долговечно. Такое грандиозное ощущение - таки простыми средствами.

На больших стройках, где работы велись сразу в нескольких пунктах, во избежание ошибок пользовались шнуром. Строились пирамиды методом последовательной кладки. С первых же лет своего правления фараон приступал к сооружению подземелья-крипты и ядра пирамиды. На протяжении всей своей жизни он продолжал постройку пирамиды и сооружал вторую погребальную камеру, которая была пышнее первой.

Пирамиды различают:

Наружные плоскости пирамид ориентированы по сторонам света. Пирамиды имеют погребальные камеры и вентилляционные шахты-каналы. 

Пирамида — это не только символом долговечности и абсолютного покоя, и служит не только усыпальницей. Многие ученые пришли к выводу, что в связи с необычайно четкой ориентацией Большой пирамиды и тем, что направление ее главной галереи совпадает с земной осью - пирамида еще, и астрономический памятник.

Щековая стена Египетских пирамид представляет собой лестницу, ступени которой служат для подноски материалов. Те ряды, по которым поднимались подносчики, выложены кирпичем положенным на ребро. Ряды кирпича идут волнистой линией. Они поднимаются и опускаются снова. Такое волнистое направление рядов объясняется употреблением шнура вместо правила (рейки). Шнур провисал и ряды становились волнистыми.

В архитектуре древнего Египта имели место и своды и купола.

Своды возводили из кирпича. История сводов в древности является историей тех приемов, при помощи которых было возможно возводить своды непосредственно над пролетами. 

Обычной формой египетских сводов является купол. Из всех древних типов свода сферический свод-купол легче всего возводится без кружал. Каждый ряд так незначительно свешивается над лежащим ниже его, что может удержаться без кружал. Как только кольцо сведено, оно уже не изменяет своей сферической формы и достаточно прочно, чтобы снести последующие ряды. Кладка исполняется тем легче, чем незначительнее свешивается внутрь одно кольцо над другим.

Египетские песчаники и известняки легко поддавались обработке. Кроме железных орудий египтяне пользовались распиловкой при помощи мокрого песка. Пилу заменяли железным лезвием или проволокой, дощечкой или веревкой. Передвигали камни при помощи салазок, их изображения сохранились на стенах каменоломни в Эль-Мазаре. Благодаря остроумному расположению канатов, камень, влекомый быками без особых приспособлений устанавливался с земли на полозья.

Обелиски создавались из глыб каменоломней Асуана. Их обрабатывали при помощи бронзовых клиньев, загнанных в борозды, заранее проведенные в гранитной скале. О перевозке обелисков писал еще Плиний: чтобы поднять обелиск его помещали между 2мя барками и с наступлением половодья Нила выводили из каменоломни.

Лотосообразные гаторические колонны в Египте, наряду с квадратными и многогранными столбами использовались также, как и круглые колонны. Стволу колонны придавали форму стебля, капители - форму цветка. Возможно, что прототипом такой лотосообразной колонны послужил декоративный мотив связки стеблей водяных растений на столбах хижин. В качестве декорирования помещений в архитектуре древнего Египта активно применялись металлические украшения.

Храмы древнего Египта — это обычно: святилище, как самая удаленная часть храма, предназначенная для пребывания божества; вокруг святилища — помещения служебного характера; перед святилищем — зал наос, доступный только для посвященных; перед наосом — обширный двор, куда допускались молящиеся.

Жилища в архитектуре древнего Египта: План египетского дома похож на план всякого азиатского жилища. Это всегда замкнутое помещение, с фасадом без окон, освещаемое только со стороны внутреннего двора; на крыше устроена терраса, где обитатели дома ночуют в жаркое время.

Зодчими в Египте становились, как правило, по наследству: от отца к сыну. Удавалось установить целые родословные архитекторов. Клейма фараонов на кирпиче встречаются даже в частных постройках.

Когда народы Европы были еще в полуварварском состоянии, в Египте уже существовали вполне развитые искусство и промышленность.

2 группа:

Архитектура Древнего Египта теснейшим образом связано с заупокойным культом. Классическим образцом архитектурных сооружений являются пирамиды фараонов 4 - й династии (27 в. до н.э.) Хеопса, Хефрена и Микерина. Их отточенная форма, основанная на пропорциях золотого сечения, была предельно лаконична и бесконечно выразительна. Два элемента определяли закономерности формы: основание, квадратное в плане, и схождение сторон в одной точке, подобно тому, как вся египетская жизнь сходилась, сфокусировалась в обожествленном фараоне. Гениальная в своей простоте пирамидальная конструкция несла художественное обобщение самой сути египетского общества, подчиненного безграничной власти фараона.

Характерной особенностью пирамид как архитектурных соображений было отношение массы и пространства: погребальная камера, где стоял саркофаг с мумией, очень небольшая, а подводили к ней длинные и узкие коридоры. Пространственный элемент был сведен к минимуму. Безраздельно господствовала масса всей пирамиды, в то время как сама пирамида была завершающей частью огромного пространственного ансамбля: на берегу Нила стоял небольшой нижний заупокойный храмик, от которого шел длинный крытый коридор. Поднимаясь по склону Ливийского плоскогорья, он подводил к верхнему заупокойному храму, расположенному у подножия пирамиды.

Пропорции в зданиях и частях зданий архитектуры Египта устанавливали между их размерами самые простые отношения 1:2, 3:5. 

Общая высота здания делилась обычно на три равные части: • Цоколь; • Ствол колонны; • и верхнюю часть здания до основания капители.

Последняя часть делится, в свою очередь, также на три части: 

Прием ритмических повторений: анфилады колонн, сдвоенные ряды сфинксов, повторяемость геометрии в статуях усиливают впечатление архитектурного комплекса.

Система пропорций, применявшаяся в архитектуре Древнего Египта, построена на квадрате и его производных. Эту систему построения ряда последовательно увеличивающихся производных квадрата мы будем называть в дальнейшем системой диагоналей.

3 группа:

В основе пропорций древнеегипетских храмов лежит золотое сечение. В построении пропорций возможны два основных метода.

1. Арифметические системы, где пропорции вычисляются абстрактным методом (по числам). Разновидностью этого способа является модульная система, при которой размер какой-либо части здания (например, диаметр колонны) принимается за единицу (модуль) и по отношению к нему все остальные размеры выражаются в простых числах.

2. Геометрические системы пропорций, где все три проекции сооружения определяются путем геометрических построений (чаще всего на основе квадрата или круга).

Наибольшую роль здесь играет принцип подобия частей.

Частным случаем геометрических построений является группа отношений так называемого «золотого сечения» (т. е. деления отрезка в среднем и крайнем отношении), при котором весь отрезок так относится к большей своей части, как большая часть относится к меньшей. Таким образом, постоянная пропорция этой системы, образуя убывающую или возрастающую прогрессию, связывает воедино все элементы здания, от больших до самых малых величин.

Золотым сечением наиболее часто занимались теоретики, исходя из квадрата, точнее из двух квадратов (Хембидж), или из деления окружности на 10 частей (Мёссель).

Оба названных исследователя приводят, кроме того, общие законы построений, объясняющие все схемы геометрических пропорций. Мёссель, например, выводит все геометрические фигуры из деления окружности на различное число частей. По Мёсселю пропорции храма Хонсу в Карнаке были определены путем вписывания его в круг (описанный веревкой на земле), разделенный на восемь частей (рис.).

Система пропорций, применявшаяся в архитектуре Древнего Египта, построена на квадрате и его производных (рис.). Эту систему построения ряда последовательно увеличивающихся производных квадрата мы будем называть в дальнейшем системой диагоналей.

Эти четыре фигуры, связанные между собой общим построением, обладают интересными свойствами.

Первая фигура — квадрат — одна из простейших фигур, имеющая равные стороны. Она является основной формой в ранней архитектуре Древнего Египта, также как и связанная с ней вторая фигура — прямоугольник с отношением сторон, равным отношению стороны квадрата к его диагонали (рис.).

Отношение сторон в нем √3/2=1,4142 или 1/√2=0,7071

Третья фигура (рис.) имеет отношение сторон 1/√3=1,7321

Половина этого прямоугольника образует прямоугольный треугольник с меньшей стороной, равной половине гипотенузы, и с углами 30° и 60°. Хорошо знакомый всем угольник с такими углами является, вероятно, самым ранним вспомогательным прибором в работе архитектора, наравне с угольником, имеющим угол 45° и равным половине квадрата.

Отношение большего катета к гипотенузе в треугольнике с углом 60° равно √3/2=0,866

Четвертая фигура представляет собой прямоугольник, составленный из двух квадратов (рис.)

В нем примечательно часто встречающееся в Египте отношение диагонали к большей стороне √5/2=1,1185, совпадающее с «функцией» золотого сечения. Отношение малого катета к диагонали 1/√5=0.4472.

Эти шесть связанных между собой величин:

1) квадрат;

2) его диагональ;

3) прямоугольный треугольник с углом 60°;

4) прямоугольник, состоящий из двух квадратов;

5) и 6) отношения его диагонали к сторонам √5/2 и 1/√5 лежат в основе пропорций большинства сооружений Древнего царства.

Иногда кроме квадрата применялся равносторонний треугольник (рис.). Он имеет уже знакомое отношение высоты к стороне √3/2:1= 0.866 или стороны к высоте 1: √3/2=1.155.

Все эти фигуры могут быть построены в натуре при помощи простой веревки. Даже прямоугольник с таким иррациональным и, казалось бы, сложным отношением сторон, как √5/2=1,118, которое является отношением диагонали двух квадратов к стороне (рис.), может быть построен этим простейшим способом (такой прямоугольник условно называется в дальнейшем неточным квадратом).

Это же отношение может быть получено при помощи диагонали полуквадрата (рис.), так как половина квадрата составляет прямоугольник в два малых квадрата.

В нем примечательно часто встречающееся в Египте отношение диагонали к большей стороне√5/2=1,11805, совпадающее с «функцией» золотого сечения. Отношение малого катета к диагонали 1/√5=0.4472.

Таким образом, в основе пропорций имеется связь математики и архитектуры, которая является золотым сечением.

Учащиеся, работавшие в группах, создали презентации, которые в дальнейшем объединили в одну.

mognovse.ru

Пропорции в египетской архитектуре 3

Главное меню:

• Всеобщая история архитектуры
• Первобытнообщинный период
• Первобытнообщинный период
• Рабовладельческое общество
• Рабовладельческое общество
  • Карта раздела «Рабовладельческое общество»
  • Рабовладельческое общество
  • Древний Египет
  • Эфиопия
  • Эгейский мир
  • Двуречье и Месопотамия
  • Передняя Азия
  • Закавказье
  • Иран
    • Иран
    • Иран. Мидия. Экбатаны. Гробницы
    • Иран. Гробницы Дукан-и-Дауд, Кызкапан и Курх-у-Кич
    • Иран. Ахеменидский период. Сузы, Персеполь
    • Иран. Пасаргады. Дворцы
    • Иран. Персеполь. Дворцы
    • Иран. Персеполь. Дворец Ксеркса
    • Иран. Дворцы Дария
    • Иран. Сузы. Дворец Дария
    • Иран. Гробницы Кира, Дария, Да-у-Духтар
    • Иран. Святилища
    • Иран. Эпоха Ахеменидов. Этапы развития архитектуры
    • Парфия
    • Парфия. Селевкия, Ктесифон
    • Парфия. Хатра
    • Парфия. Ашшур, Дура-Европос
    • Парфия. Жилые дома
    • Парфия. Дворец Хатры
    • Парфия. Дворцы Ашшура, Ниппура, Кухи-Ходжа
    • Парфия. Культовые сооружения
    • Парфия. Фортификация
    • Парфия. Гробницы
    • Парфия. Общественная архитектура
    • Иран. Сасанидское государство
    • Иран. Гур, Дарабгерда, Бишапур, Нишапур
    • Иран. Ктесифон. Фортификация городов
    • Иран. Арки, своды, купола
    • Иран. Арки, своды, купола 2
    • Иран. Дари-Шахр, Ширван, Тель-Дехаб
    • Иран. Дворец в Фирузабаде, ансамбль Бишапура
    • Иран. Дворец в Сарвистане, дворец в Ктесифоне — Таки-Кисра
    • Иран. Дворец Касри-Ширин, комплекс Хош-Кури
    • Иран. Парковые гроты Таки-Бустана
    • Иран сасанидский. Культ огня. Чортак
    • Иран сасанидский. Христианство. Культовые алтари
    • Иран. Особенности общественного строительства
    • Иран. Искусство
    • Иран. Искусство 2
  • Средняя Азия
  • Афганистан
  • Юго-Восточная Азия
  • Дальний Восток. Китай
  • Дальний Восток. Корея
  • Дальний Восток. Япония
  • Америка. Этапы развития
• Архитектура античного мира
• Архитектура античного мира
  • Карта раздела «Архитектура античного мира»
  • Архитектура античного мира
  • Архитектура древней Греции
  • Греция. Архитектура древнейшей эпохи (XII - середина VIII в. до н.э.)
  • Греция. Архитектура архаической эпохи (750-480 гг. до н.э.)
  • Архитектура греческой метрополии
  • Архитектура Великой Греции
  • Архитектура Малой Азии и островов Эгейского моря
  • Греция. Архитектура эпохи расцвета (480-400 гг. до н.э.)
  • Сооружения второй четверти V в. до н.э. вне Афин
  • Расцвет аттической архитектуры
  • Сооружения 2-й половины V в. до н.э. в Великой Греции и Малой Азии
  • Греция. Архитектура IV в. до н.э. (400—323 гг. до н.э.)
  • Греция. Архитектура эпохи эллинизма (323г. до н.э.-Iв. н.э.)
  • Греция Эллинизм. Общественные сооружения
  • Греция. Эллинизм. Культовое строительство
  • Греция. Эллинизм. Мемориальные сооружения
  • Архитектура античных государств Северного Причерноморья
  • Вклад древней Греции в мировое развитие архитектуры
  • Архитектура древнего Рима
  • Этрусская архитектура
  • Архитектура Римской республики
  • Римская республика. Общественные сооружения
  • Римская республика. Инженерные сооружения
  • Римская республика. Жилые сооружения
  • Римская республика. Виллы
  • Архитектура Римской империи
  • Римская империя. Градостроительство
  • Римская империя. Общественные сооружения
  • Римская империя. Мемориальные и триумфальные сооружения
  • Римская империя. Инженерные сооружения
  • Римская империя. Жилые сооружения
  • Римская империя. Погребальные сооружения
  • Ордер
  • Декор
  • Декор 2
  • Композиция
  • Роль римской архитектуры
  • Раннехристианская архитектура
• Архитектура Восточной Европы. Средние века
• Архитектура Восточной Европы. Средние века
  • Карта раздела «Архитектура Восточной Европы. Средние века»
  • Архитектура Восточной Европы. Средние века
  • Архитектура Восточной Европы. Средние века 2
  • Архитектура Восточной Европы. Средние века 3
  • Архитектура Восточной Европы. Средние века 4
  • Архитектура Восточной Европы. Средние века 5
  • Архитектура Византии
  • Архитектура Армении
    • Архитектура Армении
    • Архитектура IV—VII вв.
    • Архитектура IX-XI вв.
      • Развитие Армении политическое IX—XI вв
      • Развитие Армении экономическое IX—XI вв
      • Ани, Лори-берд
      • Амберд, Бджни, Каянберд, Тигнис, Магасберд, дворец Багратидов
      • Айраванка, Нарекаванка, Ованнеса, храм Креста, собор Аракелоц
      • Ани. Кафедральный собор, Гагикашен, церкви Григория Абугамренц и Спасителя
      • "Пастушья" церковь, Аракелоц, Аменапркич, Ншана
      • Храм в Мармашене, Гавиты, Татев, Хцконк, хачкар, Гавазан
    • Архитектура XII—XIV вв.
    • Архитектура киликийской Армении (1080—1375 гг.)
    • Архитектура XV—XIX вв.
    • Роль архитектуры феодальной Армении
  • Архитектура Грузии
    • Архитектура древнего времени ( IV—VII вв.)
    • Архитектура VIII—IX вв.
    • Архитектура X—XI вв.
    • Архитектура XII—XIII вв.
    • Архитектура XIII—XV вв.
    • Архитектура XVI—XVIII вв.
  • Архитектура Болгарии
  • Архитектура Сербии и Македонии
    • Сербия и Македония. Особенности развития
    • Сербия и Македония. Особенности развития 2
    • Градостроительство. Крепости, замки, монастыри
    • Градостроительство. Замки, монастыри, жилые дома
    • Культовая архитектура раннефеодального периода
    • Период господства Византии
    • Рашская архитектурная школа
    • Рашская архитектурная школа. Храмы. Тип, материалы
    • Рашская архитектурная школа. Храмы. Интерьеры. Пропорции. Декор
    • Македонская и косовско-метохийская школа. Храмы. Формы, планы, особенности
    • Македонская и косовско-метохийская школа. Храмы. Формы, декор
    • Моравская школа. Храмы. Форма, особенности
    • Моравская школа. Храмы. Форма, материал, декор
    • Моравская школа. Храмы. Декор. Фрески
    • Роль архитектуры Сербии и Македонии
  • Архитектура Молдавии и Валахии

archisto.info

Законы пропорций и оптических иллюзий в архитектуре Древнего Египта

ПРОПОРЦИИ

Чем достигается пропорциональность? Создается ли она инстинктивным чувством гармонии или является результатом основанного на определенном методе графического построения? Сравнивая отдельные части египетских зданий, обычно мож­но установить между их размерами самые простые отношения, например 1 : 2 или 3 : 5. И почти всегда эти отношения можно выразить общей мерой в целых числах.

При кладке здания из кирпича такой единицей измерения является кирпич. Кирпичи изготовляются одного размера и, чтобы использовать их целиком, не обсекая, размеры здания должны быть взяты в кратном отношении к размерам кирпича. Таким образом, кирпич является общей единицей измерения или естественным «модулем».

В конструкциях из тесаного камня приходится считаться с такой же, хотя, быть может, менее настоятельной, необходимостью выражать размеры в целых числах. Только при этом условии можно обеспечить правильный и непрерывный ход работ. Египтяне имели разработанную систему мер. Инстинкт и практический опыт заставили их подчинять все размеры единому модулю. Такая единица измерения является обязательным модулем для всех частей здания. С появлением понятия меры и пропорции всего естественнее было остановиться на простейших из них, из которых неизбежно вытекает закон простых отношений.

Арифметические отношения. — Рисунок 36 показывает применение простых отношений в египетских памятниках. Здесь дан чертеж Элефантинского храма. Обмер произведен архитекторами, сопровождавшими египетскую экспедицию Наполеона.

Установлены   следующие   соотношения   отдельных   частей здания.

Общая высота здания делится на три равные части:

1.      Цоколь.

2.      Ствол колонны.

3.      Верхняя часть здания до основания капители.

Последняя часть делится в свою очередь также на три части:

1.     Капитель.

2.     Абака и архитрав.

3.     Карниз.

Каждое подразделение выражается целым числом в единице меры, равняющейся одному египетскому футу (36 см), и точно соответствует двум таким футам. Мы находим здесь одновременно простые отношения и целые числа; в этом — вся сущность пропорций.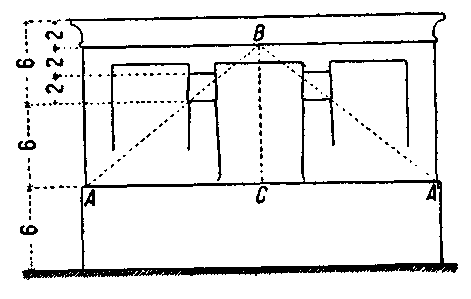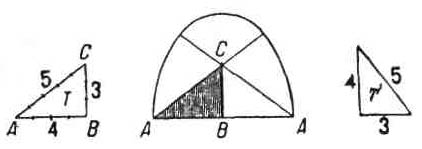

Рис. 36	Рис. 37

Геометрические отношения. — Но египтяне не ограничивались арифметическими отношениями. Их склонности к геометризму отвечали изящные геометрические построения. Известно древнее решение задачи прямоугольного треугольника, где прямой угол определяется при помощи треугольника, стороны которого относятся друг к другу, как 3:4:5. Плутарх сообщает, что этот треугольник с соизмеримыми сторонами считался египтянами священным, и они часто пользовались им. Так, при начертании сводов они поступали следующим образом (рисунок 37):

Кривая сводов описывалась циркулем из трех центров, взятых в точках А, Си А двух египетских треугольников. При разработке проектов зданий это вело к установлению таких пропорций, при которых в контуры здания мог быть вписан указанный треугольник. Из этих треугольников, служивших для установления пропорций, обычно пользовались лишь треугольниками с соизмеримыми сторонами в отношении 3:4:5 (треугольник Т или Т, рисунок 37) или треугольниками рисунка 38, которые составляются из сочетания в ином порядке сторон, выраженных числами 3,4 и 5.

В Элефантинском храме в основу пропорций положен треугольник R (рисунок 38). На чертеже рисунка 36 изображено, каким образом он вписывается в контур фасада.

Кроме треугольников, берущих свое начало от египетских треугольников со сторонами 3, 4 и 5, встречаются другие треугольники, изображенные на рисунке 39 буквами E,G и М.

Е — равносторонний треугольник;

G — треугольник, полученный путем сечения по диагональной плоскости пирамиды Хеопса, профиль которой — равносторонний треугольник;

М— треугольник, высота которого получается делением основания в крайнем и среднем отношении.

На первый взгляд применение этих треугольников противоречит принципу модуля и простых отношений. Перед нами как будто два взаимно исключающих друг друга метода построения, один — посредством чисел, другой — посредством треугольников.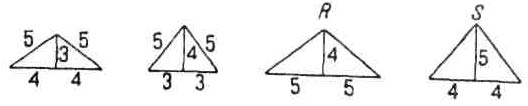

Рис. 38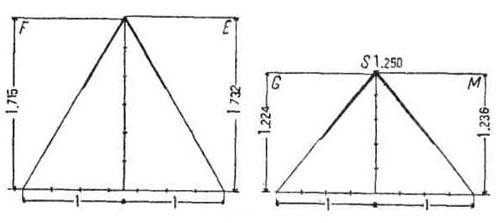

Рис. 39

Согласование арифметического и графического методов. — Интересно отметить, что фактически метод треугольников и метод модульных отношений дают почти совпадающие результаты и что в пределах обычных приближений применение треугольников дает простые отношения размеров, иначе говоря, оба метода сливаются в один. Эти наблюдения сделаны Бабеном. Рисунок 39 наглядно показывает совпадение результатов обоих методов.

В группе Е, F мы накладываем на равносторонний треугольник другой треугольник, у которого высота равна 6/7 основания. Контуры их почти совпадают. По сторонам можно вычислить величину отклонения. Треугольник с отношением высоты к основанию, равным 7 : 8, почти не отличается от равностороннего.

В группе G, S, M (S — производный от египетского треугольника со сторонами 3, 4 и 5) при наложении усматривается такое же совпадение. Следовательно, оба метода, несмотря на то, что их часто противопоставляли друг другу, дают одинаковые результаты. Нужна исключительная точность постройки и точнейшие способы измерения ее частей, чтобы установить, что именно было положено в ее основу — арифметический ли расчет или геометрические комбинации треугольников. При построении равностороннего треугольника или треугольника, высота которого равна 6/7 основания, линии их совпадают.

При разделении прямой в среднем и крайнем отношении, или при разделении ее на две части с отношением 5 : 3 фактически получается одно и то же. Отношения 5 : 3 и 6 :7 согласуют простые арифметические отношения с замечательными геометрическими свойствами. Частое повторение пропорций, совпадающих с начертанием треугольников, данных на рисунке 39, позволяет думать, что этими треугольниками действительно руководились при постройках. Положение можно резюмировать следующим образом.

Египтяне придерживались модульных пропорций и простых отношений; из простых отношений они предпочтительно пользовались такими, которые совпадают с геометрическими построениями. Впечатление гармонии усиливается выбором таких модульных пропорций, которые отвечают понятию изящного.

Практическое значение метода. — С точки зрения практического строительства арифметические отношения и построения, полученные посредством треугольников, поддаются наглядному изображению, которое позволяет зодчему без помощи письма передать свой замысел, установить правила и создать школу.

С точки зрения гармонии форм значение метода еще важнее. Идея единства в произведении искусства есть основной закон создания ансамбля. Мы чувствуем сущность и значение этого закона, еще не осознавая его. Дисгармония в музыке, ложно прочувствованные пропорции в архитектуре оскорбляют наше эстетическое чувство, заложенное в человеческой природе. Зодчеству нужна определенная закономерность, и безразлично, в чем она находит свое выражение — в геометрии или в числах.

Из всех остальных законов закон простых отношений кажется наиболее обязательным. Он распространяется не на одну только архитектуру. В музыке ему подчиняется число колебаний, в мелодии — это такт, в стихе — ритм. Древнейшее зодчество ритмично, и этим сразу определяются и его принцип и система применения. Египтяне, а вслед за ними и греки, достигали гармонии модульными комбинациями. Следует ли из этого, что и нам надо идти этим путем? Отнюдь нет. Ведь мы не подчиняем нашу живую речь закону древней просодии. Но там, где этот ритм был соблюден, он пробуждает в нас идею гармонии, рождающую чувство красоты.

СИММЕТРИЯ, РИТМИЧЕСКОЕ ПОВТОРЕНИЕ, ОПТИЧЕСКИЕ ИЛЛЮЗИИ

Египетское искусство достигает особой выразительности приемом ритмических повторений. Анфилады колонн, сдвоенные ряды сфинксов, одинаковость поз в статуях усиливают впечатление архитектурного комплекса.

Симметрия — господствующая особенность египетского искусства. Ни одна архитектура не уравновешивает так массы, как египетская. Нигде не умели так использовать естественные условия для достижения определенного впечатления. Луксорский храм представляет ряд дворов, имеющих форму неправильных прямоугольников. Египетским зодчим было известно, что глаз неверно воспринимает углы плана, и потому они допускали некоторые неправильности, ускользающие от зрителя. Обелиски А и В (рисунок 40), стоявшие когда-то перед входом в храм, были различной величины. Для того чтобы создать иллюзию двух обелисков одинаковой высоты, меньший из них В был выдвинут на передний план. Впечатление глубины во дворе Рамессеума усиливается благодаря постепенному уменьшению колонны по мере их удаления, для чего воспользовались подъемом почвы. В настоящее время этот прием обычно применяется в театральных декорациях.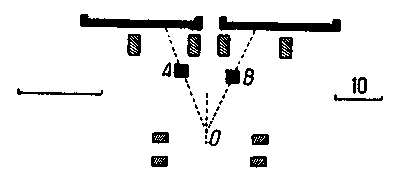

Рис. 40

Рис. 41

Умение египтян использовать законы оптических иллюзий превзошли только греки. Как доказал Паннеторн, египтянам был известен странный обман зрения, получающийся при восприятии длиной горизонтальной линии. Так, например, линия архитрава кажется провисшей посредине. Греки боролись с этой оптической иллюзией, придавая архитраву выгиб в направлении, противоположном кажущемуся искривлению (рисунок 41, Р). В храме Мединет Абу нет этого выгиба, но архитрав в плане представляет кривую, показанную на рисунке 41, М. Перспективный эффект тот же. В обоих случаях кривизна эта едва заметна. На чертежах же она для большей наглядности сильно подчеркнута.

Намеренные изменения точных геометрических линий, нюансировку, возможную только в утонченном, вполне овладевшем своими методами искусстве, мы будем рассматривать в связи с греческой архитектурой.

Укажем здесь лишь на общность тенденций и на глубокий анализ законов оптического восприятия в египетском зодчестве, которое на тысячу лет опередило в этом отношении греческое искусство.

Глава «Законы пропорций и оптических иллюзий» раздела «Архитектура Древнего Египта» из книги Огюста Шуази «История архитектуры» (Auguste Choisy, Histoire De L'Architecture, Paris, 1899). По изданию Всесоюзной академии архитектуры, Москва, 1935 г.

totalarch.ru

Законы пропорций и оптических иллюзий в архитектуре Древнего Египта | Архитектура Древнего мира

Глава «Законы пропорций и оптических иллюзий» раздела «Архитектура Древнего Египта» из книги Огюста Шуази «История архитектуры» (Auguste Choisy, Histoire De L'Architecture, Paris, 1899). По изданию Всесоюзной академии архитектуры, Москва, 1935 г.

Пропорции

Чем достигается пропорциональность? Создается ли она инстинктивным чувством гармонии или является результатом основанного на определенном методе графического построения? Сравнивая отдельные части египетских зданий, обычно мож­но установить между их размерами самые простые отношения, например 1 : 2 или 3 : 5. И почти всегда эти отношения можно выразить общей мерой в целых числах.

При кладке здания из кирпича такой единицей измерения является кирпич. Кирпичи изготовляются одного размера и, чтобы использовать их целиком, не обсекая, размеры здания должны быть взяты в кратном отношении к размерам кирпича. Таким образом, кирпич является общей единицей измерения или естественным «модулем».

В конструкциях из тесаного камня приходится считаться с такой же, хотя, быть может, менее настоятельной, необходимостью выражать размеры в целых числах. Только при этом условии можно обеспечить правильный и непрерывный ход работ. Египтяне имели разработанную систему мер. Инстинкт и практический опыт заставили их подчинять все размеры единому модулю. Такая единица измерения является обязательным модулем для всех частей здания. С появлением понятия меры и пропорции всего естественнее было остановиться на простейших из них, из которых неизбежно вытекает закон простых отношений.

Арифметические отношения. — Рисунок 36 показывает применение простых отношений в египетских памятниках. Здесь дан чертеж Элефантинского храма. Обмер произведен архитекторами, сопровождавшими египетскую экспедицию Наполеона.

Установлены   следующие   соотношения   отдельных   частей здания.

Общая высота здания делится на три равные части:

1.      Цоколь.

2.      Ствол колонны.

3.      Верхняя часть здания до основания капители.

Последняя часть делится в свою очередь также на три части:

1.     Капитель.

2.     Абака и архитрав.

3.     Карниз.

Каждое подразделение выражается целым числом в единице меры, равняющейся одному египетскому футу (36 см), и точно соответствует двум таким футам. Мы находим здесь одновременно простые отношения и целые числа; в этом — вся сущность пропорций.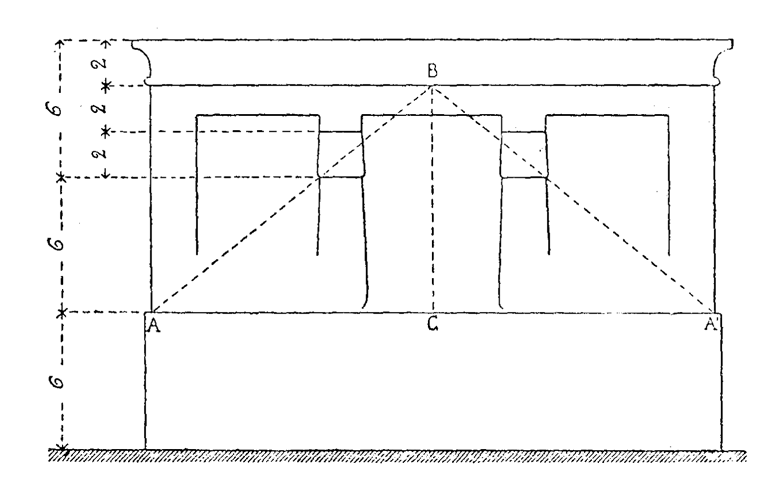

Рис. 36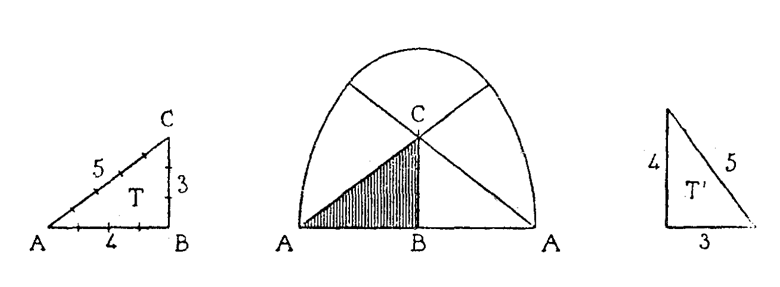

Рис. 37

Геометрические отношения. — Но египтяне не ограничивались арифметическими отношениями. Их склонности к геометризму отвечали изящные геометрические построения. Известно древнее решение задачи прямоугольного треугольника, где прямой угол определяется при помощи треугольника, стороны которого относятся друг к другу, как 3:4:5. Плутарх сообщает, что этот треугольник с соизмеримыми сторонами считался египтянами священным, и они часто пользовались им. Так, при начертании сводов они поступали следующим образом (рисунок 37):

Кривая сводов описывалась циркулем из трех центров, взятых в точках А, Си А двух египетских треугольников. При разработке проектов зданий это вело к установлению таких пропорций, при которых в контуры здания мог быть вписан указанный треугольник. Из этих треугольников, служивших для установления пропорций, обычно пользовались лишь треугольниками с соизмеримыми сторонами в отношении 3:4:5 (треугольник Т или Т, рисунок 37) или треугольниками рисунка 38, которые составляются из сочетания в ином порядке сторон, выраженных числами 3,4 и 5.

В Элефантинском храме в основу пропорций положен треугольник R (рисунок 38). На чертеже рисунка 36 изображено, каким образом он вписывается в контур фасада.

Кроме треугольников, берущих свое начало от египетских треугольников со сторонами 3, 4 и 5, встречаются другие треугольники, изображенные на рисунке 39 буквами E,G и М.

Е — равносторонний треугольник;

G — треугольник, полученный путем сечения по диагональной плоскости пирамиды Хеопса, профиль которой — равносторонний треугольник;

М— треугольник, высота которого получается делением основания в крайнем и среднем отношении.

На первый взгляд применение этих треугольников противоречит принципу модуля и простых отношений. Перед нами как будто два взаимно исключающих друг друга метода построения, один — посредством чисел, другой — посредством треугольников.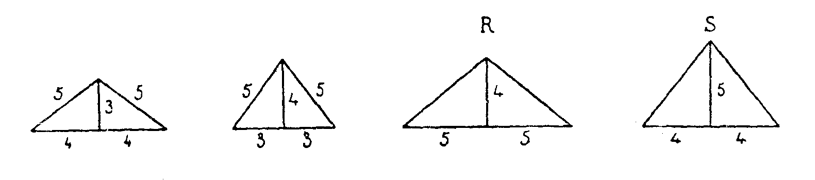

Рис. 38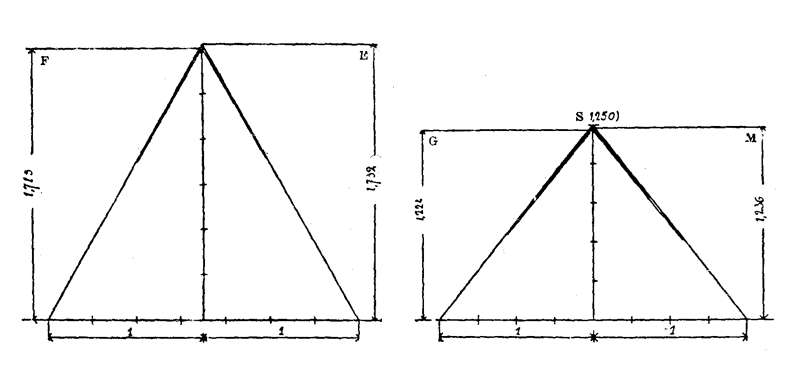

Рис. 39

Согласование арифметического и графического методов. — Интересно отметить, что фактически метод треугольников и метод модульных отношений дают почти совпадающие результаты и что в пределах обычных приближений применение треугольников дает простые отношения размеров, иначе говоря, оба метода сливаются в один. Эти наблюдения сделаны Бабеном. Рисунок 39 наглядно показывает совпадение результатов обоих методов.

В группе Е, F мы накладываем на равносторонний треугольник другой треугольник, у которого высота равна 6/7 основания. Контуры их почти совпадают. По сторонам можно вычислить величину отклонения. Треугольник с отношением высоты к основанию, равным 7 : 8, почти не отличается от равностороннего.

В группе G, S, M (S — производный от египетского треугольника со сторонами 3, 4 и 5) при наложении усматривается такое же совпадение. Следовательно, оба метода, несмотря на то, что их часто противопоставляли друг другу, дают одинаковые результаты. Нужна исключительная точность постройки и точнейшие способы измерения ее частей, чтобы установить, что именно было положено в ее основу — арифметический ли расчет или геометрические комбинации треугольников. При построении равностороннего треугольника или треугольника, высота которого равна 6/7 основания, линии их совпадают.

При разделении прямой в среднем и крайнем отношении, или при разделении ее на две части с отношением 5 : 3 фактически получается одно и то же. Отношения 5 : 3 и 6 :7 согласуют простые арифметические отношения с замечательными геометрическими свойствами. Частое повторение пропорций, совпадающих с начертанием треугольников, данных на рисунке 39, позволяет думать, что этими треугольниками действительно руководились при постройках. Положение можно резюмировать следующим образом.

Египтяне придерживались модульных пропорций и простых отношений; из простых отношений они предпочтительно пользовались такими, которые совпадают с геометрическими построениями. Впечатление гармонии усиливается выбором таких модульных пропорций, которые отвечают понятию изящного.

Практическое значение метода. — С точки зрения практического строительства арифметические отношения и построения, полученные посредством треугольников, поддаются наглядному изображению, которое позволяет зодчему без помощи письма передать свой замысел, установить правила и создать школу.

С точки зрения гармонии форм значение метода еще важнее. Идея единства в произведении искусства есть основной закон создания ансамбля. Мы чувствуем сущность и значение этого закона, еще не осознавая его. Дисгармония в музыке, ложно прочувствованные пропорции в архитектуре оскорбляют наше эстетическое чувство, заложенное в человеческой природе. Зодчеству нужна определенная закономерность, и безразлично, в чем она находит свое выражение — в геометрии или в числах.

Из всех остальных законов закон простых отношений кажется наиболее обязательным. Он распространяется не на одну только архитектуру. В музыке ему подчиняется число колебаний, в мелодии — это такт, в стихе — ритм. Древнейшее зодчество ритмично, и этим сразу определяются и его принцип и система применения. Египтяне, а вслед за ними и греки, достигали гармонии модульными комбинациями. Следует ли из этого, что и нам надо идти этим путем? Отнюдь нет. Ведь мы не подчиняем нашу живую речь закону древней просодии. Но там, где этот ритм был соблюден, он пробуждает в нас идею гармонии, рождающую чувство красоты.

Симметрия, ритмическое повторение, оптические иллюзии

Египетское искусство достигает особой выразительности приемом ритмических повторений. Анфилады колонн, сдвоенные ряды сфинксов, одинаковость поз в статуях усиливают впечатление архитектурного комплекса.

Симметрия — господствующая особенность египетского искусства. Ни одна архитектура не уравновешивает так массы, как египетская. Нигде не умели так использовать естественные условия для достижения определенного впечатления. Луксорский храм представляет ряд дворов, имеющих форму неправильных прямоугольников. Египетским зодчим было известно, что глаз неверно воспринимает углы плана, и потому они допускали некоторые неправильности, ускользающие от зрителя. Обелиски А и В (рисунок 40), стоявшие когда-то перед входом в храм, были различной величины. Для того чтобы создать иллюзию двух обелисков одинаковой высоты, меньший из них В был выдвинут на передний план. Впечатление глубины во дворе Рамессеума усиливается благодаря постепенному уменьшению колонны по мере их удаления, для чего воспользовались подъемом почвы. В настоящее время этот прием обычно применяется в театральных декорациях.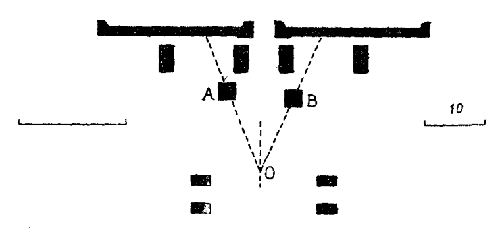

Рис. 40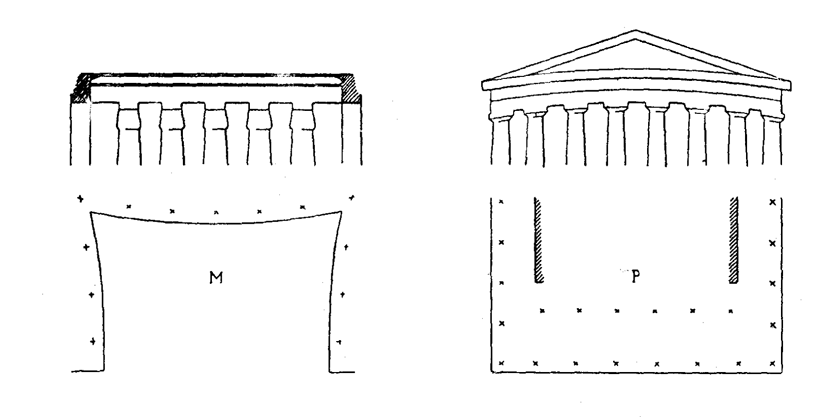

Рис. 41

Умение египтян использовать законы оптических иллюзий превзошли только греки. Как доказал Паннеторн, египтянам был известен странный обман зрения, получающийся при восприятии длиной горизонтальной линии. Так, например, линия архитрава кажется провисшей посредине. Греки боролись с этой оптической иллюзией, придавая архитраву выгиб в направлении, противоположном кажущемуся искривлению (рисунок 41, Р). В храме Мединет Абу нет этого выгиба, но архитрав в плане представляет кривую, показанную на рисунке 41, М. Перспективный эффект тот же. В обоих случаях кривизна эта едва заметна. На чертежах же она для большей наглядности сильно подчеркнута.

Намеренные изменения точных геометрических линий, нюансировку, возможную только в утонченном, вполне овладевшем своими методами искусстве, мы будем рассматривать в связи с греческой архитектурой.

Укажем здесь лишь на общность тенденций и на глубокий анализ законов оптического восприятия в египетском зодчестве, которое на тысячу лет опередило в этом отношении греческое искусство.

archaic.totalarch.com

Каноны пропорциональности Древнего Египта

Рис. 1.3. Египетский канон 60 основанный на прямоугольном треугольнике 3,4,5 (Arkkitekhti-Arkitekten 1962 №9)

Рис. 1 .9 . Система вписанных и описанных квадратовВ Египте также применялась система пропорционирования на основе вписанных квадратов. Она давала геометрический ряд с отношением 1: л/2, в котором чередовались иррациональные и целые простые числа (рис. 1.9).Эта система использовалась как в Египте, так и в более поздние времена, например в Средневековье, для построенияготических башен; отношение стороны к диагонали квадрата связывают древнерусскую са-жентьт с косой саженью.

Некоторые современники основывают свое учение о пропорциях на золотом сечении. Н. А. Померанцева в исследовании «Эстетические основы искусства Древнего Египта» пишет: «Пропорции золотого сечения в искусстве Древнего Египта присутствуют во всех без исключения памятниках, поскольку они заложены в самой природе — в строении листа, человеческого тела и т. д. Однако в чистом виде эти пропорции охватывались древними мастерами интуитивно, что способствовало обобщенности восприятия образа, выявлению его сущности».

Следует отметить, что нет никаких данных, подтверждающих использование египтянами золотого сечения, но его присутствие прослеживается во многих памятниках Древнего Египта, начиная от пирамид и кончая произведениями малых форм — роспись, рельеф, скульптура. Обнаружить его можно путем обмера, принимая за исходную величину наибольший размер композиции (исходя из длины, ширины или высоты)(рис. 1.11—1.14).

Теория пропорций египетского искусства и архитектуры, созданная А. Фурнье де Кора в процессе длительных математических и в, частности, геометрических исследований, по сути своей очень близка к золотому сечению. Автор называет ее «божественной гармонией». В основе этой теории лежат математические соотношения между числом п, которое египтяне вычисляли, и корнем Ф, а также восемь соотношений, первое из которых А = (10 + 5л/5)/д = 9,47214 Они меняются с изменением числителя. (Результаты приблизительно соответствуют: ф 2 + Ф4 для А, для N, Ф, Е + Ф2 + 1,1 = Ф2 и т. д.). Они определенно указывают на разные случаи применения отношения золотого сечения: будь то скульптура, роспись, рельеф или архитектурное произведение. Вместе с тем существуют противоположные мнения, когда использованиезолотого сечения приписывается случайности (рис. 1.10).

В Древнем Египте система построения пропорций основывается на квадрате и его производных, а потому с этим связана и с иррациональными величинами, т. е. прямоугольниками, образующимися как функции проведенных диагоналей. Диагональ квадрата √2 становится большей стороной первого прямоугольника (1 √2). Диагональ этого прямоугольника принимается за большую сторону следующего (1:√3), и наконец получается удвоенный квадрат 1:2, диагональ которого равняется л/5 (об этом будет подробно говорится в другой главе этой книги, в той, которая знакомит с ролью золотого сечения в композиции греческих архитектурных форм и методом Дж. Хэмбиджа). Этот метод В. Н. Владимиров назвал «системой диагоналей» с примечанием, что в отдельных случаях применения этих пропорций может идти речь об их близости к золотому сечению.

Рис. 1.10. Соотношения «божественной гармонии» по А Фурнье де Кора. В этом сложном нлетении линий выделено восемь пропорциональных отношений — производных от стороны квадрата М. При условном модуле М= 21,18 соразмерные линии имеют следующие иррациональные значения: А - 9,47: С = 8,09; 5 ~ 5,85;О - 5,00: N = 4,23; Е = 3,61; I = 2,61

Суммируя шесть взаимосвязанных пропорциональных величин: квадрат диагонали прямоугольник (1: -ч/З), содержащий в себетреугольник с углами 60° и 30°, прямоугольник, составленный из двух квадратов и отношение V5/2 и v5/l, — Владимиров считает, что именно эти соотношения применяли архитекторы и художники Древнего Египта.

К этому он добавляет еще одну простую геометрическую фигуру — равносторонний треугольник. И наконец, первостепенное значение он придает квадрату, напоминая, что «на ранней стадии развития егинетской архитектуры задача построения пропорций была неотделима от задачи измерения и обмера строений на природе и возникла, вероятно, на основе реальной практики строителя. При этом значение квадрата обусловлено тем, что он служит мерой площади».

gestaltung.ru

Смотрите также

• 
  Символы древнего китая
• 
  Исландский древний поэт
• 
  Древний исландский поэт
• 
  Демоны древнего мира
• 
  Фото древняя посуда
• 
  Древний орнамент рим
• 
  Карта древнего новгорода
• 
  Порнофильмы древний рим
• Фила древняя греция
• 
  Виды древних религий
• 
  Персия древняя правители