Так считали древние. Египет. Как считали древние египтяне
Так считали древние. Египет :: NoNaMe  Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне. Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне.----------------------<cut>---------------------- Меня всегда немного интересовал древний Египет. Ну, во-первых, Египет — одно из первых государств, о котором мы много знаем, и кроме того, это очень великое государство, которое оставило огромное наследие. Я не имею в виду огромные размеры пирамид. Даже наша письменность и латинская, и кириллическая восходит к древнему Египту. Мне также всегда нравилась египетская скульптура, и мода брить голову у женщин и мужчин. Это кажется очень современным. Но это статья не о художественной культуре. Так что приступим. Цифры и числа Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так:  Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание. Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет:  Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право. Теперь насчет дробей. Для трех дробей существовали специальные значки:  Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14  Все правильные дроби записывались как сумма таких дробей. Например:  На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби: 4/5= 1/2 + 1/4+ 1/203/4= 1/2 +1/4» Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали. Сложение и умножение Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача. Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22 1 222 444 88 8 уже больше, чем 7, поэтому табличка заканчивается на четырех. Теперь 1+2+4=7 значит 22+44+88=154. Хотите верьте, хотите нет но 154 это верный ответ. Конечно в египетской записи (я не знаю, как она точно выглядела) такие вычисления были проще, ведь умножать на 2 в египетской записи очень просто. Еще пример, немного сложнее: 13 умножить на 57 1* 572 1144* 2288* 456 1+4+8=13 и 57+228+456=741 Иногда, чтобы ускорить процесс прибегали к умножению на 10. Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*20+0*21+1*22+1*23 т.е. 1+100+ 1000=1101 Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17:Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого. 1 172 344 688 136 Здесь нужно составить число 238 из чисел второго столбца, начиная с конца. 136+68+34=238, значит нам нужны числа 8+4+2=14. Итак, 238/17 =14 К несчастью, деление не всегда приводит к целому числу. В ряде случаев это было довольно сложно.Я покажу простой пример, заимствованный мной из одной книги. Разделим 213 на 8Сначала все, как обычно. 1 82* 164 328* 6416* 128 Здесь мы останавливаемся, ведь 128 на 2 = 256, а это больше 213. 128+64<213. 128+64+32 уже опять больше. Не подходит. 128+64+16<213 Пока все ОК. 128+64+16+8 уже больше. Значит мы смогли набрать только 208=128+64+16 из 213.И нам осталось разделить 213-208=5Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4. 1/2* 41/4 21/8* 1 Таким образом, окончательный результат будет 213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8 Сейчас мы имеем удачный случай, но так получается не всегда. txapela.ru Так считали древние. Египет Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне. Меня всегда немного интересовал древний Египет. Ну, во-первых, Египет — одно из первых государств, о котором мы много знаем, и кроме того, это очень великое государство, которое оставило огромное наследие. Я не имею в виду огромные размеры пирамид. Даже наша письменность и латинская, и кириллическая восходит к древнему Египту. Мне также всегда нравилась египетская скульптура, и мода брить голову у женщин и мужчин. Это кажется очень современным. Но это статья не о художественной культуре. Так что приступим. Цифры и числа Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так: 
Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание. Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет: 
Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право. Теперь насчет дробей. Для трех дробей существовали специальные значки: 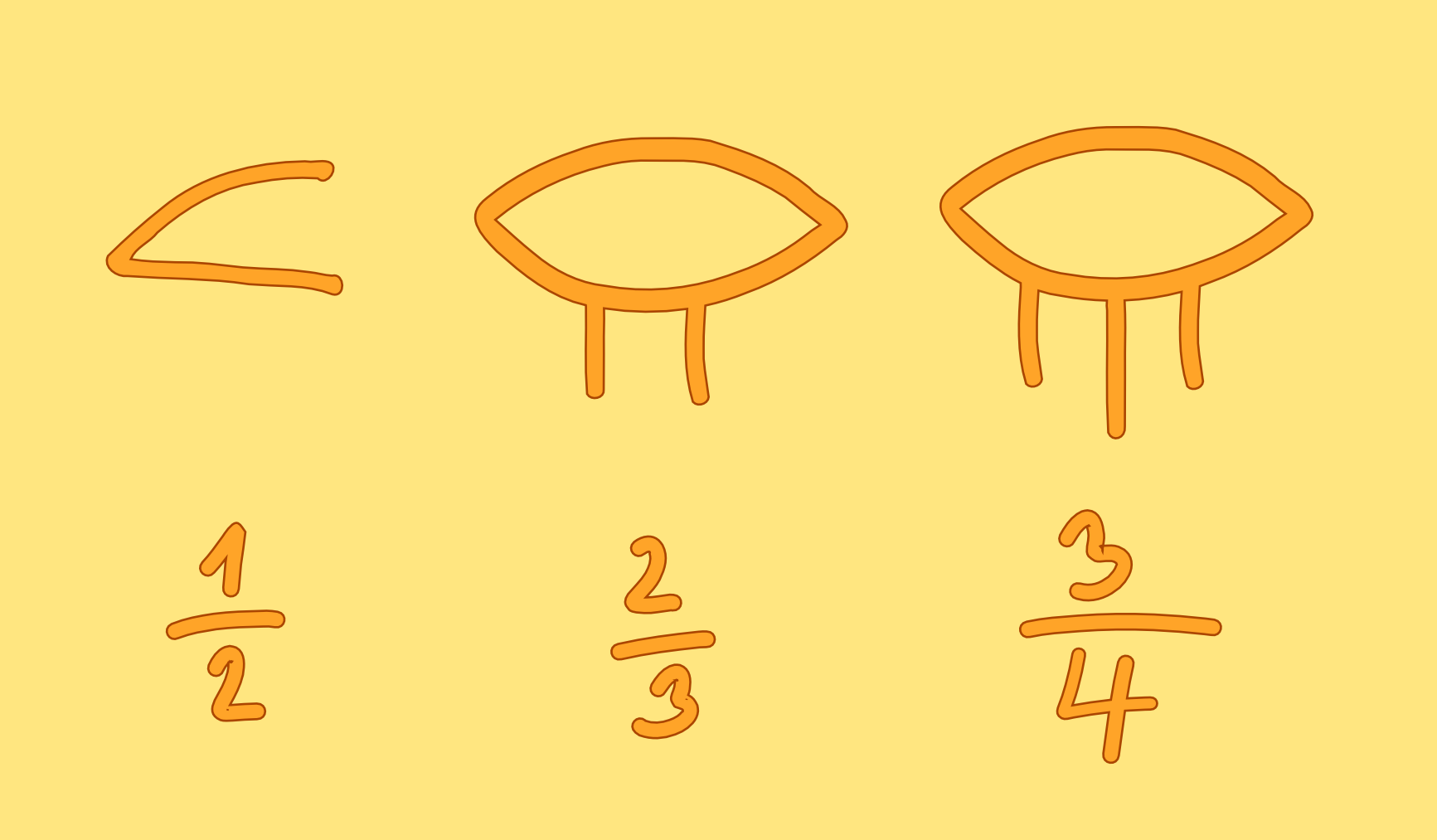
Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14 Все правильные дроби записывались как сумма таких дробей. Например: Все правильные дроби записывались как сумма таких дробей. Например: На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:4/5= 1/2 + 1/4+ 1/203/4= 1/2 +1/4»Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали. На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:4/5= 1/2 + 1/4+ 1/203/4= 1/2 +1/4»Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали. Сложение и умножение Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача.Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22 8 уже больше, чем 7, поэтому табличка заканчивается на четырех. Теперь 1+2+4=7 значит 22+44+88=154. Хотите верьте, хотите нет но 154 это верный ответ. Конечно в египетской записи (я не знаю, как она точно выглядела) такие вычисления были проще, ведь умножать на 2 в египетской записи очень просто. Еще пример, немного сложнее: 13 умножить на 57 | 1* | 57 | | 2 | 114 | | 4* | 228 | | 8* | 456 |
1+4+8=13 и 57+228+456=741Иногда, чтобы ускорить процесс прибегали к умножению на 10. Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*20+0*21+1*22+1*23 т.е. 1+100+ 1000=1101Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17:Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого. Здесь нужно составить число 238 из чисел второго столбца, начиная с конца. 136+68+34=238, значит нам нужны числа 8+4+2=14. Итак, 238/17 =14 К несчастью, деление не всегда приводит к целому числу. В ряде случаев это было довольно сложно. Я покажу простой пример, заимствованный мной из одной книги. Разделим 213 на 8Сначала все, как обычно. | 1 | 8 | | 2* | 16 | | 4 | 32 | | 8* | 64 | | 16* | 128 |
Здесь мы останавливемся, ведь 128 на 2 = 256, а это больше 213. 128+64<213. 128+64+32 уже опять больше. Не подходит. 128+64+16<213 Пока все ОК. 128+64+16+8 уже больше. Значит мы смогли набрать только 208=128+64+16 из 213. И нам осталось разделить 213-208=5Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4. Таким образом, окончательный результат будет213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8Сейчас мы имеем удачный случай, но так получается не всегда. Автор: Sychuan Источник www.pvsm.ru Как жили древние египтяне? | Наука будущего С чем у нас ассоциируется древний Египет? Фараоны, пирамиды, загадки о том, кем они и как были построены, мифология, а также библейские сюжеты. О жизни древних египтян мы практически ничего не знаем. Да нам и негде было узнать: краткий школьный курс построен так, что просто нам рассказывает о том, что было такое государство и существовало оно в такие-то годы. Может еще расскажет про Клеопатру и то, как в нее был влюблен был Марк Антоний. В данной статье вы можете прочитать факты о жизни древних египтян, которые заставят вас по-другому посмотреть на этот народ, живший задолго до начала нашей эры и зарождения цивилизаций в Европе. 
Раздельный прием пищи Египтяне считали, что неправильно есть всей семьей. Муж, жена, дети – все ели раздельно, чтобы не отвлекаться от пищи на пустые разговоры, а также не тратить это время на ссоры. У знати во время трапезы допускались к столу только слуги. Интересный факт: даже во время завтраков было принято пить пиво. Не любили обувь Египтяне считали, что обувь стесняет движения, не позволяет чувствовать землю, которая является даром их богов. Потому, как правило, они ходили босиком. Этого придерживались даже фараоны и жрецы. Обувь была символом царства мертвых, потому всегда занимала одно из главных мест во время похорон. Но обувь носили, особенно, если у человека были враги. Люди писали их имена на подошве и с каждым шагом растаптывали своих противников об землю. Любили домашних животных Древние египтяне заводили не только кошек, но и собак, ибисов, обезьян и других птиц. Даже, если им ничего не надо было охранять, они все равно держали дома собаку, даже если они не любили охоту, то могли завести сокола. Почему? Потому что они любили животных. Настолько, что часто заказывали мумии для мертвых питомцев, чтобы потом встретиться с ними в загробном мире. Женщины ходили с открытой грудью Оголенная женская грудь в древнем Египте не была чем-то постыдным. Наоборот, она подчеркивалась специальными платьями. В ней не было ничего сакрального или запретного, потому и надобность в ее защите от посторонних глаз отсутствовала. Любили, когда приятно пахнет Египтяне были помешаны на приятных запахах. Чтобы не расставаться с любимым ароматом, они носили на голове специальные конусы, наполненные воском и благовониями. От жары вся это смесь плавилась и от людей шел приятый аромат. Это, кстати, одни из первых в мире духов. Прически у детей 
Если у взрослых был большой выбор причесок, так и париков, то с детьми была другая история. Все они должны были носить определенную, которую сегодня называют «сапожок». Длинные волосы по бокам и сбритый затылок. Зачем? Ученые до сих пор спорят, но основная теория заключается в том, что у этого было религиозное значение. Любили пиво Как было сказано выше, египтяне очень любили пиво и пили его даже на завтрак. Оно было настолько популярным, что во многие времена и во многих городах заменяло даже деньги и являлась нормальной заработной платой для рабочих. Также местное пиво очень легко утоляло жажду, несмотря на крепость, кислинку и то, что оно было немного горьким. Поделиться в социальных сетях science-future.top Древние египтяне Википедия | Цивилизация Древнего мира • Северо-Восточная Африка | | Древний Египет | | Пирамида Хефрена и Большой Сфинкс в некрополеИнбу-хедж (др.-греч. Мемфис, совр. Гиза) | Другие названия | Та-кемет, Та-мери, Та-уи, Кеми | • экзотопонимы | — Мицраим, Мудраия, Миср, Маср | Время | сер. 4 тыс. до н. э. — IV-VII вв. н. э. | • периодизация | — Додинастический Египет (как часть доисторического периода)— Династический Египет (РЦ, СТЦ, ППП, СЦ, ВПП, НЦ, ТПП, Поздний)— Эллинистический Египет— Римский Египет— Византийский Египет (позд. античность/ранее средневек.) | Локализация | Северо-Восточная Африка | • колыбель | — АРЕ, только мухафазы вдоль реки Нил и оазис Файюм | • макс. границы | — Нубия, Синай, Киренаика, Палестина | Население | протоегиптяне, египтяне, копты | • осн. этногенез | — кушиты, ливийцы, семиты, греки-македоняне | • прочие | — гиксосы, евреи, финикийцы, греки-ионяне, греки-карийцы | Язык | египетский язык | • письменность | — египетское письмо (иероглифика, иератика, демотика) | Религия | древнеегипетская (список богов) | | Древний Египет на Викискладе |
Древний Еги́пет (от др.-греч. Αἴγυπτος и лат. Aegyptus), самоназвание Та-кемет, Та-мери, Та-уи и др. (транслит. егип. tA-kmt, tA-mrj, tA-wy), Ке́ми (копт. Ⲭⲏⲙⲓ) — название исторического региона и культуры значительной цивилизации Древнего мира, существовавшей на северо-востоке Африки вдоль нижнего течения реки Нил. История Древнего Египта составляет около 40 веков и подразделяет ru-wiki.ru Так считали древние. Египет / СоХабр Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне. Меня всегда немного интересовал древний Египет. Ну, во-первых, Египет — одно из первых государств, о котором мы много знаем, и кроме того, это очень великое государство, которое оставило огромное наследие. Я не имею в виду огромные размеры пирамид. Даже наша письменность и латинская, и кириллическая восходит к древнему Египту. Мне также всегда нравилась египетская скульптура, и мода брить голову у женщин и мужчин. Это кажется очень современным. Но это статья не о художественной культуре. Так что приступим. Цифры и числа Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так: Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание.
Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет: Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право.
Теперь насчет дробей. Для трех дробей существовали специальные значки: Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14
Все правильные дроби записывались как сумма таких дробей. Например:
На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:4/5= 1/2 + 1/4+ 1/20
3/4= 1/2 +1/4»
Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали. Сложение и умножение Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача.
Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22 8 уже больше, чем 7, поэтому табличка заканчивается на четырех. Теперь 1+2+4=7 значит 22+44+88=154. Хотите верьте, хотите нет но 154 это верный ответ. Конечно в египетской записи (я не знаю, как она точно выглядела) такие вычисления были проще, ведь умножать на 2 в египетской записи очень просто. Еще пример, немного сложнее: 13 умножить на 57| 1* | 57 | | 2 | 114 | | 4* | 228 | | 8* | 456 |
1+4+8=13 и 57+228+456=741 Иногда, чтобы ускорить процесс прибегали к умножению на 10. Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*20+0*21+1*22+1*23 т.е. 1+100+ 1000=1101 Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17: Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого. Здесь нужно составить число 238 из чисел второго столбца, начиная с конца. 136+68+34=238, значит нам нужны числа 8+4+2=14. Итак, 238/17 =14 К несчастью, деление не всегда приводит к целому числу. В ряде случаев это было довольно сложно. Я покажу простой пример, заимствованный мной из одной книги. Разделим 213 на 8 Сначала все, как обычно.| 1 | 8 | | 2* | 16 | | 4 | 32 | | 8* | 64 | | 16* | 128 |
Здесь мы останавливемся, ведь 128 на 2 = 256, а это больше 213. 128+64 Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4. Таким образом, окончательный результат будет213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8 Сейчас мы имеем удачный случай, но так получается не всегда. sohabr.net Так считали древние. Египет Posted by: robot 3 years, 9 months ago http://geektimes.ru/post/240900/Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне.
Меня всегда немного интересовал древний Египет. Ну, во-первых, Египет — одно из первых государств, о котором мы много знаем, и кроме того, это очень великое государство, которое оставило огромное наследие. Я не имею в виду огромные размеры пирамид. Даже наша письменность и латинская, и кириллическая восходит к древнему Египту. Мне также всегда нравилась египетская скульптура, и мода брить голову у женщин и мужчин. Это кажется очень современным. Но это статья не о художественной культуре. Так что приступим. Цифры и числа
Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так:
Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание.
Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет:
Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право.
Теперь насчет дробей. Для трех дробей существовали специальные значки:
Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14
Все правильные дроби записывались как сумма таких дробей. Например:
На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:4/5= 1/2 + 1/4+ 1/20
3/4= 1/2 +1/4»
Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали. Сложение и умножение
Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача.
Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22 8 уже больше, чем 7, поэтому табличка заканчивается на четырех. Теперь 1+2+4=7 значит 22+44+88=154. Хотите верьте, хотите нет но 154 это верный ответ. Конечно в египетской записи (я не знаю, как она точно выглядела) такие вычисления были проще, ведь умножать на 2 в египетской записи очень просто. Еще пример, немного сложнее: 13 умножить на 57| 1* |
57 |
| 2 |
114 |
| 4* |
228 |
| 8* |
456 |
1+4+8=13 и 57+228+456=741 Иногда, чтобы ускорить процесс прибегали к умножению на 10. Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*20+0*21+1*22+1*23 т.е. 1+100+ 1000=1101 Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17: Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого. Здесь нужно составить число 238 из чисел второго столбца, начиная с конца. 136+68+34=238, значит нам нужны числа 8+4+2=14. Итак, 238/17 =14 К несчастью, деление не всегда приводит к целому числу. В ряде случаев это было довольно сложно. Я покажу простой пример, заимствованный мной из одной книги. Разделим 213 на 8 Сначала все, как обычно.| 1 |
8 |
| 2* |
16 |
| 4 |
32 |
| 8* |
64 |
| 16* |
128 |
Здесь мы останавливемся, ведь 128 на 2 = 256, а это больше 213. 128+64 Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4. Таким образом, окончательный результат будет213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8 Сейчас мы имеем удачный случай, но так получается не всегда. Share on Twitter Share on Facebook news.shamcode.ru
|
