Понятие о средних величинах, их значение. Виды средних величин и их расчет. Древний закон средних величин
Тема 5 средние величины Тема 5: Средние величины и показатели вариации Вопросы: 5.1.Общие принципы применения средних величин. (Виды средних) 5.2.Степенные средние. 5.3 Структурные средние. 5.1.Общие принципы применения средних величин Средние величины - это величины, которые позволяют охарактеризовать явление по количественно варьирующему признаку. Общие принципы применения средних величин. При определении средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные. Средняя величина должна, прежде всего, рассчитываться по однородной совокупности. Качественно однородные совокупности позволяет получить метод группировок, который всегда предполагает расчет системы обобщающих показателей. Общие средние должны подкрепляться групповыми средними.
Средние величины существуют в различных видах и формах. Выбор вида и формы средней зависит от вида осредняемого признака и наличия исходных данных. 5.2 Степенные средние Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Выбор формы средней зависит от того, в каком виде представлены данные: если они сгруппированы, т.е. одно и то же значение признака встречается несколько раз, используются взвешенные средние; если каждое значение признака встречается только один раз, средняя рассчитывается в простой форме.
Выбор вида средней зависит от вида осредняемого признака и от наличия исходных данных. В.Е.Овсиенко формализовал порядок выбора формы средней качественного признака на основе следующих правил: Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должная вычисляться по формуле средней арифметической взвешенной. Если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической,
3. В том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя вычисляется непосредственно по этой формуле. Таблица 1- Виды и формы средних величин | Вид степенной средней | Показатель степени, m | Формула расчета | | простая | взвешенная | Общий вид
| m | = | = | Гармоническая
| -1 | | | Геометрическая
| → 0 | | | Арифметическая
| 1 | | | Квадратическая
| 2 | | | Кубическая
| 3 | | |
где - среднее значение признака; хi - индивидуальные значения осредняемого признака; n - количество единиц совокупности; fi - частота (вес) индивидуальных значений осредняемого признака; wi = xifi - произведение индивидуального значения признака и его частоты. Главное требование к формуле расчета среднего значения: все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей.
Свойства средней арифметической Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет. Произведение средней () на сумму частот (∑f) равно сумме произведения отдельных вариантов на соответствующие им частоты (∑хf) (расхождения – за счет округлений):
∑f = ∑хf (5.1) Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
(5.2) Если все осредняемые варианты уменьшить или увеличить на постоянное число А , то средняя арифметическая соответственно уменьшиться или увеличиться на ту же величину:
(5.3) Если все индивидуальные значения признака (т. е. все варианты) увеличить либо уменьшить в одно и то же число раз (или на одно и то же число), то среднее значение получившегося нового признака будет во столько же раз (или на столько же) отличаться от среднего значения исходного показателя
(5.4) Величина средней арифметической не изменится, если веса всех вариантов умножить или разделить на одно и то же число
(5.5) 5.3. Структурные средние Помимо средних величин, в статистическом анализе используются и структурные средние: мода и медиана. Мода - это значение признака, которое чаще всего встречается в ряде распределения. В дискретных рядах модой является значение признака в той группе, у которой наблюдается наибольшая частота. Определить моду в этом случае можно визуально. В интервальных рядах распределения мода также находится в той группе, у которой наибольшая частота. Но так как в интервальных рядах признак может принимать любое значение в заданном интервале, точное значение моды следует определять по специальной формуле: (10) где хмо - нижняя граница модального интервала; iмо - величина модального интервала; fмо - частота модального интервала; f(мо-1) - частота интервала, предшествующего модальному; f(мо+1) - частота интервала, следующего за модальным. Модальным является интервал, имеющий наибольшую частоту!!!!!!!!! Значение моды, рассчитанное по формуле, не может быть меньшим, чем нижняя граница модального интервала, и не будет превышать верхнюю границу модального интервала. Медиана - это значение признака, стоящего в центре ранжированного ряда распределения. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – больше его. Для ранжированного дискретного ряда с нечетным числом членов, медиана – варианта, расположенная в центре. Для ранжированного дискретного ряда с четным числом членов, медиана равна средней арифметической из двух вариант, расположенных в центре. В дискретном ранжированном ряду распределения медиана равна значению признака в той группе, у которой сумма накопленных частот равна или превышает половину суммы всех частот ряда распределения. Сумма накопленных частот находится последовательным сложением частот каждой группы. Так, для первой группы сумма накопленных частот будет равна частоте этой группы, для второй группы - сумме частот первой и второй группы, для третьей группы - сумме частот первой, второй и третьей группы и т.д. накопленная частота последней группы будет равна общей сумме частот ряда распределения. В интервальном ряде распределения медиана находится по специальной формуле: (11) где хме - нижняя граница медианного интервала; iме - величина медианного интервала; fме - частота медианного интервала; Σf - сумма всех частот ряда распределения; Sме-1 - сумма частот, накопленных до медианного интервала. Медианным считается интервал, сумма накопленных частот которого равна или превышает половину всех частот ряда распределения!!!!!!!!!! Значение медианы будет не меньше, чем значение нижней границы медианного интервала, и не превысит значения верхней границы медианного интервала. По соотношению моды, медианы и средней можно судить о характере распределения признака. Распределение может бытьсимметричным. В этом случае наблюдается равенство между модой, медианой и средним значением признака (рис.5.1). | частота признака, (fi) | у | | | | Мо= Ме = . | | | | | | | | | | | | | | | | | | | | | | | | | | | значение признака (хi) | | | | | | | |
Рис. 5.1- Симметричный ряд распределения Если между модой, медианой и средней выполняется соотношение (Мо < Ме < ), то мы имеем дело справосторонней асимметрией. (рис. 5.2) | частота признака, (fi) | | | | | | | у | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | значение признака (хi) | х |
Рис. 5.2- Ряд распределения с правосторонней асимметрией При наличии левосторонней асимметрии мода, медиана и средняя связаны следующим образом: | частота признака, (fi) | у | | | Мо> Ме> | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | значение признака (хi) | х |
Рис. 3. Ряд распределения с левосторонней асимметрией Определить наличие асимметрии можно и с помощью относительного показателя - коэффициента асимметрии. Он может быть рассчитан в двух вариантах - на основе моды или медианы. , (5.8) . (5.9) Если As > 0, имеется правосторонняя асимметрия, если As < 0 - левосторонняя. 7 studfiles.net Средние величины. Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признания в статистической совокупности в конкретных условиях места и времени. Средняя величина выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из выражающих признаков. Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Средняя величина будет типичной только тогда, когда она будет рассчитана по качественно однородной совокупности. Например используя для расчета средние величины доходов: служащих государственных, совместных предприятий, наука, культура и т.п., является крайне неоднородной. В этом и других случаях метод средних используется в сочетании с методом группировок: если совокупность не однородна – общее среднее должны быть занесены или дополнены групповыми средними, т.е. средними, рассчитанными по по качественно однородным группам. Виды средних и методы их расчета. В практике статистической обработки материала возникают различные задачи, имеются особенности изучаемых явлений и поэтому для их решения требуются различные средние. Математическая статистика выводит различные средние из формул степенной средней: == При Z = 1 ср. арифметическая Z = 0 ср. геометрическая Z =-1 ср. гармоническая Z =2 ср. квадратическая Однако вопрос о том, какой вид средней необходимо применить в отдельном случае, разрешается путем конкретного анализа изучаемой совокупности введем следующие понятия: 1 признак по которому находится средняя называется осредняемым признаком () 2 величина осредняемого признака у каждой единицы совокупности называется индивидуальным значением осредняемого признака или вариантами (х; х2; х3….хn) 3 Чаcтота – это повторяемость индивидуальных значений признака (f) Средняя арифметическая – распространенная. Она исчисляется в тех случаях, когда объем определяемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. В зависимости от характера исходных данных средняя арифметическая определяется следующим образом: 1 Н-р Найти средний стаж работы 10 работников: 6,5,4,3,3,4,5,4,5,4, т.е. даны одиночные значения = =(6+5+4+3+3+4+5+4+5+4)/10 = 43/10 = 4,3года Когда значение признака встречается несколько раз.
Средня взвешенная арифметическая = или = Пример расчета | Взвешенная дискретная | Взвешенная интервальная | | Оценки, получаемые на экзамене по математике | Число неявок на занятия | | оценки | Кол-во студентов | Группы по числу неявок | Число студентов | | 2 3 4 5 | 1 2 10 7 | интервальный | дискретный | | До5 6-10 11-15 16-20 >20 | 8-5=3 8 5 3 1 | 3 8 5 3 1 | | Итого: | 20 | Итого: | | 20 |
= (2*1+3*2+4*10+5*7)/20=83/20 = 4.15 =3*3+8*8+13*5+18*3+23/20 = 215/20=10.75 Свойства средней арифметической П-р Продажа акций АО «Дока хлеб» на торгах фондовой секции ТБМ «Гермес» | Сумма | Кол-во проданных акций, шт. | Курс продажи, руб. | | 1 | 500 | 1080 | | 2 | 300 | 1050 | | 3 | 1100 | 1145 |
1 средняя арифметическая из постоянных чисел равна этому постоянному числу Если х = а. Тогда = 2 Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно Ито же число, то нового ряда от этого не изменится. Уменьшатся все f в к раз. = = 1112.89=1112.9 Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна 0, т.е.
из-за округления. 4 Если все варианты уменьшить или увеличить на какое- либо число, то среднее арифметическое нового ряда уменьшится или увеличится на столько же. X1 = x-a Курс продажи увеличился в 1,5 раза, т.е. на 50% 5Если все варианты уменьшить или увеличить в к раз, то среднее арифметическое нового ряда уменьшится или увеличится во столько же, т.е. в к раз Пусть Отсюда в полтора раза иногда роль частот при исчислении средней играет частота (w) . Посчитаем частоты во втором примере W, % 15; 40; 25; 15; 5; Средняя гармоническая. Это величина обратная средней арифметической, когда z=-1. Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется средне гармоническая взвешенная. Н-р, расчет средней цены Средняя цена = | Город | Цена, руб. хi | реализации т.р.Wi | Частоты fi = | | А | 30 | 600 | 20 | | Б | 20 | 1000 | 50 | | В | 35 | 350 | 10 | | Итого: | | 1950 | 80 |
Известны: 1 реализации 2 Цена Найти: Кол-во реализованных единиц. Неверный путь. простая Где - сумма обратных значений вариант n – число вариант M=fx Применение: для расчета некоторых индексов, в частности индекса цен. Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии Z=0 т.е. прямой подставленной средняя не выводится.n – число вариант Пример Доходы населения России представлены табл. | 1985г. | 244,7 млрд. | | 1986г | 283,6 млрд. | | 1987г | 264,3 млрд. | | 1988г | 287,2 млрд. | | 1989г | 324,6 млрд. | | 1990 г | 384,7 млрд. |
Рассчитать средне годовой доход населения Решение 1 найдем цепные Тр 1985г 1986г 253,6/244,7 =1,04 1987г 264,3/253,6 =1,04 1988г 1,09 1989г 1,13 1990г 1,18 Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношением двух чисел. Поэтому ср. геометрическая используется в расчетах ср. годовых темпов роста. простая взвешенная где х – вариант осредняемого критерия П – произведение вариантов f – частота вариантов Средняя квадратичная. Z=2 = В экономических исследованиях ср. квад. в измененном виде широко используется для характеристики вариации признака (дисперсия, среднее квадратическое отклонение). Между степенными средними существует следующая зависимость: чем больше показатель степени, тем > значение средней. | Значение к | -1 | 0 | 1 | 2 | и т.д. | | Отношение м\у сред | < | < | < | < | и т.д. |
Соотношение это называется правилом мажорантности. Формула ср. арифметической взвешенной m1i+A , где m1= Средняя m1 из значений называется моментом 1 порядка, а способ вычисления средней – способом моментов. Иногда его называют способом отсчета от условного нуля. Расчет среднего арифметического способом « условного нуля ». | Валовая продукция, млн. руб | Число пред, % | Середина шт. ед. х | х - 225 | | | | До 50 | 3 | 25 | -200 | -4 | -12 | | 50-100 | 6 | 75 | -150 | -3 | -18 | | 100-150 | 10 | 125 | -100 | -2 | -20 | | 150-200 | 21 | 175 | -50 | -1 | -21 | | 200-250 | 33 | 225 | 0 | 0 | 0 | | 250-300 | 18 | 275 | 50 | 1 | 18 | | Более 300 | 9 | 325 | 100 | 2 | 18 | | итого | 100 | - | - | - | -35 |
Пример на решение задачи с применением свойств средней. | х | f | x*100 | х*100-48 | f | f*х/ | | 0,13 | 200 | 13 | -35 | 2 | -70 | | 0,28 | 250 | 28 | -20 | 2,5 | -50 | | 0,33 | 300 | 33 | -15 | 3 | -45 | | 0,48 | 350 | 48 | 0 | 3,5 | 0 | | 0,53 | 300 | 53 | +5 | 3 | 15 | | 0,68 | 200 | 68 | 20 | 2 | 40 | | итого | 1600 | | | 16 | -110 |
Свойство 1. При увеличении х в 100 раз средняя арифметическая увеличивается в 100 раз. Свойство 2. Правило условного нуля. Свойство 3.При уменьшении f в 100 раз средняя не меняется. Структурные средние величины. Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними. К таким показателям относятся мода и медиана. Модой (Мо) называется чаще всего встречающийся вариант, или модой называется то значение признака, которое соответствует max точке теоретической кривой распределения. | Для дискретных рядов | Для интервальных рядов | | Размер обуви | Число купленных пар | f | Стаж(лет) | Число работников | F/ | | 34 35 36 37 38 39 40 | 2 10 20 88 19 9 2 | 2 12 32 120 139 148 | До 2 2-4 4-6 6-8 8-10 свыше 10 | 4 23 20 35 11 7 | 4 27 47 82 93 100 | | итого | 150 | итого | 100 |
Мо- это варианта с наибольшей частотой Мо= 37,т.к. fmax =88 Мо приближенно считают центральный вариант модального интервала, т.е., того интервала, который имеет наибольшую частоту (частость). В пределах интервала когда найти то значение признака, который является модой. Если распределение симметрично, то в качестве моды будет середина модального интервала, ото в том случае, если соседние с модальными, мало отличаются друг от друга. В ряду может использовано мод. Наикратное значение моды для интервального ряда. Мо= Хмо+ hмо (f мо- fмо-1) (fмо-fмо-1)+(fмо-fмо-1) Хо+К* f2-f1 (f2-f1)(f2-f3) Где хмо - нижняя граница модального интервала hмо - величина модального интервала fмо -частота модального интервала fмо-1 – частота предшествующая модальному интервалу fмо+1-частота , интервала, следующегоза модальным. Модальный интервал от 6-8 Мо= 6+2 35-20 6+ 30 35-20+35-11 = 39 = 6+0,77=6,77года Мо применяется: 1 при изучении цен на рынках 2 при изучении спроса населения на определенный товар т.е. мода характеризует типичность. Медиана. Ме называется значение признака у средней единицы ранжированного ряда Ранжированный ряд -это ряд, у которого значения признака записаны в порядке возрастания или убывания. Что бы найти Ме определяется: 1 Порядковый № сумма f четное, то ; еслиn-нечетное , то 2 по накопленной частоте определяем ее значение. | Дискретный ряд | Интервальный | | Ме определяется по накопленной частоте и номеру Ме. накопленная частота 120 показывает, что купленных пар не привышают 37 размер, а 32, что 32 пары. => 75 пара будет 37р. | где Ме – нужная граница медианного интервала h- величина медианного интервала - порядковый № ме fме-1- частота (частость) наполненная до медианного интервала . fме – частота(частость)медианного интервала. |
Ме находит практическое применение вследствие особого свойства абсолютных отклонений членов ряда от Ме есть величина наименьшая Ме находит широкое практическое применение в маркетинговой деятельности. Величины, приходящиеся на ¼ и ¾ расстояния от начала ряда называется нижний квартиль, а ¾ и ¼ верхний квартиль. Т.е. квартиль это варианты, делящие ряд на 4 равные части. Дециль- варианты, делящие ранжированный ряд на 10 равных частей 1 дециль 1/10 к 9/10 2 дециль2/10 к 8/10 и т.д. процентиль – на 100 равных частей. Соотношение между , Мо и Ме. 1 Если = Мо = Ме, то распределение симметрично, т.е. группа симметрична. 2 Ме < при небольшой группе с большими числами. 3 < Ме при большой концентрации данных и не очень больших числах. 4 Мо < , если совокупность неоднородна 5 Мо > , если совокупность небольшая и Мо отчетливо выражена. Все рассмотренные формы степенной средней обладают важным свойством(в отличие от структурных средних)- в формулу определения средней входят все значения ряда т.е. на размеры средней оказывают влияние значение каждого варианта. С одной стороны, это весьма положительное свойство т.к. в этом случае учитывается действие всех причин воздействующих на все единицы изучаемой совокупности. С другой стороны, даже одно наблюдение попавшее в исходные данные случайно может существенным образом исказить представление об уровне развития изучаемого признака в рассматриваемой совокупности. Особенно большое значение это имеет для коротких рядов. studfiles.net Понятие о средних величинах, их значение. Виды средних величин и их расчет.
Средняя величина — это обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Объективность и типичность статистической средней обеспечивается лишь при определенных условиях.
Первое условие - средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок.
Второе условие - для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.
Средние величины делятся на два больших класса:
степенные средние,относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
структурные средние.рассматриваются мода и медиана.
Степенные средние в зависимости от представления исходных данных могут быть:
простыми
взвешенными
Простая средняя считается по несгруппированным данным и имеет следующий общий вид:
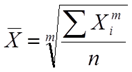
где
хi - варианта (значение) определенного признака,
m – показатель степени средней.
n – число вариант (значений).
Взвешенная средняя считается по сгруппированным данным и имеет вид:
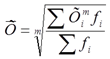
где
хi - варианта (значение) определенного признака или серединные значения интервала, в котором измеряется варианта,
m – показатель степени средней.
fi – частота, показывающая сколько раз встречается i-е значение осредняемого признака.
Общие формулы расчета степенных средних имеют показатель степени m.
В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:
средняя гармоническая, если m = -1
средняя геометрическая, если m > 0
средняя арифметическая, если m = 1
средняя квадратическая, если m = 2
средняя кубическая, если m = 3

Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.
Средняя квадратическая применяется для расчета среднего квадратического отклонения ( σ ), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).
Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики.
Структурные средние. Их расчет в дискретном и интервальном рядах распределения.
Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности.
Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
Для совокупности 3;4;2;4;3;3 мода равна 3


Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. Если число n вариант нечётно, то медиана равна варианте под номером (n + 1)/2



infopedia.su Виды средних Большое распространение в статистике имеют средние величины. Средняя величина - это обобщающий показатель, в котором находят отражение действия общих условий и закономерностей изучаемого явления. Средняя - это один из распространенных приемов обобщений. Правильное понимание сущности средней, определяет ее особую значимость в условиях рыночной экономики, когда средняя через единичное и случайное, позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др. Статистические средние рассчитываются на основе данных, правильно организованного массового наблюдения (сплошного и выборочного). Однако статистическая средняя будет объективна и типична, если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений). Например, если рассчитывать среднюю заработную плату в кооперативах и на госпредприятиях, а результат распространить на всю совокупность, то средняя фиктивна, так как рассчитана по неоднородной совокупности, и такая средняя теряет всякий смысл. При помощи средней происходит как бы сглаживание различий в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения. При этом, обобщая общее свойство совокупности, средняя затушевывает (занижает) одни показатели и завышает другие. Например, средняя выработка продавца зависит от многих причин: квалификации, стажа, возраста, формы обслуживания, здоровья и т. д. Средняя выработка отражает общее свойство всей совокупности. Средняя величина является отражением значений изучаемого признака, следовательно, измеряется в той же размерности, что и этот признак. Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. Чтобы получить полное и всестороннее представление об изучаемой совокупности по ряду существенных признаков в целом, необходимо располагать системой средних величин, которые могут описать явление с разных сторон. Важнейшим условием научного использования средних величин в статистическом анализе общественных явлений является однородность совокупности, для которой исчисляется средняя. Одинаковая по форме и технике вычисления, средняя в одних условиях (для неоднородной совокупности) фиктивная, а в других (для однородной совокупности) соответствует действительности. Качественная однородность совокупности определяется на основе всестороннего теоретического анализа сущности явления. Существуют различные виды средних в форме простoй или взвешенной: Для определения средних величин используются следующие формулы: (кликабельно) 
Правило мажорантности средних: чем выше показатель степени m, тем больше величина средней. 
Средняя арифметическая величина обладает следующими свойствами: - Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю.
- Если все значения признака (х) увеличить (уменьшить) в одно и то же число Kраз, то средняя увеличится (уменьшится) в K раз.
- Если все значения признака (x) увеличить (уменьшить) на одно и то же число A, то средняя увеличится (уменьшится) на это же число А.
- Если все значения весов (f) увеличить или уменьшить в одно и то же число раз, то средняя не изменится.
- Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Одновременное использование некоторых свойств позволяют упростить расчет средней арифметической: можно из всех значений признака вычесть постоянную величину А, разности сократить на общий множитель K, а все веса fразделить на одно и то же число и, по измененным данным, рассчитать среднюю. Затем, если полученное значение средней умножить на K, а к произведению прибавить А, то получим искомое значение средней арифметической по формуле: Полученная, таким образом, преобразованная средняя, называется моментом первого порядка, а вышеизложенный способ расчета средней — способом моментов, или отсчетом от условного нуля. Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины, в качестве значения признака в группах, принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака необходимо определять экспертным путем, исходя из сущности свойств признака и совокупности. При отсутствии возможности экспертной оценки, значения признака в открытых интервалах для нахождения недостающей границы открытого интервала, применяют размах (разность между значениями конца и начала интервала) соседнего интервала (принцип «соседа»). Иными словами — ширину (шаг) открытого интервала определяют по величине рядом стоящего интервала. helpstat.ru Сущность и виды средних величин в статистике и способы их вычисления. Виды средних величин в статистике кратко: примеры, таблицаНачиная изучение такой науки, как статистика, следует понимать, что она содержит (как и любая наука) много терминов, которые необходимо знать и понимать. Сегодня мы разберём такое понятие, как средняя величина, и выясним, на какие виды она делится, как их вычислять. Ну а перед тем как начать, поговорим немного об истории, и о том, как и зачем возникла такая наука, как статистика. 
ИсторияСамо слово "статистика" ведёт своё происхождение из латинского языка. Это производное от слова "статус", и означает "положение вещей" или "ситуация". Это короткое определение и отражает, по сути, весь смысл и назначение статистики. Она собирает данные о положении вещей и позволяет анализировать любые ситуации. Работой со статистическими данными занимались ещё в Древнем Риме. Там проводился учёт свободных граждан, их владений и собственности. Вообще изначально статистика использовалась для получения данных о количестве населения и их благах. Так, в Англии в 1061 году была проведена первая в мире перепись населения. Ханы, царствовавшие на Руси в 13 веке, тоже проводили переписи, чтобы брать дань с захваченных земель. Каждый использовал статистику для своих целей, и в большинстве случаев это приносило ожидаемый результат. Когда люди осознали, что это не просто математика, а отдельная наука, которую нужно изучать основательно, начали появляться первые учёные, заинтересованные в её развитии. Люди, которые впервые заинтересовались этой областью и начали активно её постигать, были приверженцами двух основных школ: английской научной школы политических арифметиков и немецкой описательной школы. Первая возникла в середине 17-го века и ставила целью представить общественные явления, используя числовые показатели. Они стремились выявить закономерности в общественных явлениях на основе изучения статистических данных. Сторонники описательной школы также описывали социально-общественные процессы, но с использованием только слов. Они не могли представить динамику событий, чтобы лучше понять её. В первой половине 19 века возникло ещё одно, третье направление этой науки: статистико-математическое. Огромный вклад в развитие этого направления внёс известный учёный, статистик из Бельгии Адольф Кетле. Именно он выделил виды средних величин в статистике, и по его инициативе начали проводиться международные конгрессы, посвящённые этой науке. С начала 20 века в статистике начали применяться более сложные математические методы, например, теория вероятностей. Сегодня статистическая наука развивается благодаря компьютеризации. С помощью различных программ каждый может построить график на основе предложенных данных. В интернете также есть масса ресурсов, предоставляющих любые статистические данные о населении и не только. В следующем разделе мы разберём, что означают такие понятия, как статистика, виды средних величин и вероятности. Далее коснёмся вопроса о том, как и где мы можем использовать полученные знания. Это наука, основной целью которой является обработка информации для изучения закономерностей процессов, происходящих в обществе. Таким образом, можно сформулировать вывод о том, что статистика изучает общество и те явления, что протекают в нём. Различают несколько дисциплин статистической науки: 1) Общая теория статистики. Разрабатывает методы сбора статистических данных и является основой всех остальных областей. 2) Социально-экономическая статистика. Она изучает макроэкономические явления с точки зрения предыдущей дисциплины и количественно характеризует общественные процессы. 3) Математическая статистика. Не всё в этом мире можно исследовать. Что-то приходится предугадывать. Математическая статистика изучает случайные величины и законы распределения вероятности в статистике. 4) Отраслевая и международная статистка. Это узкие области, которые изучают количественную сторону явлений, происходящих в определённых странах или отраслях жизни общества. А сейчас мы рассмотрим виды средних величин в статистике, кратко расскажем об их применении в других, не столь тривиальных областях, как статистика. 
Виды средних величин в статистикеВот мы и подошли к самому главному, собственно, к теме статьи. Конечно, для освоения материала и усвоения таких понятий, как сущность и виды средних величин в статистике необходимы определённые знания математики. Для начала вспомним, что такое среднее арифметическое, гармоническое, геометрическое и квадратичное. Среднее арифметическое мы проходили ещё в школе. Оно вычисляется очень просто: мы берём несколько чисел, среднее между которыми необходимо найти. Складываем эти числа и делим сумму на их количество. Математически это можно изобразить следующим образом. У нас есть ряд чисел, как пример, самый простой ряд: 1,2,3,4. Всего у нас 4 числа. Их среднее арифметическое находим таким образом: (1+2+3+4)/4 = 2,5. Всё просто. Мы начинаем с этого, потому что так легче понять виды средних величин в статистике. Кратко расскажем также и о среднем геометрическом. Возьмём такой же ряд чисел, как и в предыдущем примере. Но теперь, чтобы вычислить среднее геометрическое, нам нужно извлечь корень степени, которая равна количеству этих чисел, из их произведения. Таким образом, для предыдущего примера получим: (1*2*3*4)1/4~2,21. Повторим понятие среднего гармонического. Как можно вспомнить из школьного курса математики, чтобы посчитать этот вид среднего, нам необходимо сначала найти числа, обратные числам ряда. То есть мы делим единицу на это число. Так получаем обратные числа. Отношение их количества к сумме и будет средним гармоническим. Возьмём для примера тот же ряд: 1, 2, 3, 4. Обратный ряд будет выглядеть так: 1, 1/2, 1/3, 1/4. Тогда среднее гармоническое можно посчитать так: 4/(1+1/2+1/3+1/4) ~ 1,92. Все эти виды средних величин в статистике, примеры которых мы рассмотрели, являются частью группы под названием степенные. Также существуют структурные средние, которые мы разберём позже. Сейчас остановимся на первом виде. 
Степенные средние величиныМы уже разобрали арифметическое, геометрическое и гармоническое. Есть также более сложный вид, называемый средним квадратичным. Хоть его и не проходят в школе, вычислить его достаточно просто. Необходимо лишь сложить квадраты чисел ряда, разделить сумму на их количество, и извлечь из всего этого квадратный корень. Для нашего излюбленного ряда это будет выглядеть так: ((12+22+32+42)/4)1/2= (30/4)1/2 ~ 2,74. На самом деле это всё только частные случаи среднего степенного. В общем виде это можно описать так: степенное n-ного порядка равно корню степени n из суммы чисел в n-ной степени, делённой на количество этих чисел. Пока всё не так сложно, как кажется. Однако даже степенное среднее является частным случаем одного вида - среднего Колмогорова. По сути, все способы, которыми мы находили разные усреднённые величины до этого, можно представить в виде одной формулы: y-1*((y(x1)+y(x2)+y(x3)+...+y(xn))/n). Здесь все переменные x - это числа ряда, а y(x) - некая функция, по которой мы считаем среднее значение. В случае, скажем, со средним квадратичным, это функция y=x2, а со средним арифметическим y=x. Вот какие сюрпризы нам иногда преподносит статистика. Виды средних величин мы разобрали ещё не до конца. Помимо средних существуют ещё и структурные. Поговорим о них. Структурные средние величины статистики. МодаТут всё немного сложнее. Чтобы разобрать эти виды средних величин в статистике и способы их вычисления, нужно основательно подумать. Существует две основных структурных средних: мода и медиана. Разберёмся с первым. Мода встречается наиболее часто.Она применяется чаще всего для определения спроса на ту или иную вещь. Чтобы найти её значение, нужно сначала найти модальный интервал. Что это такое? Модальный интервал - область значений, где какой-либо показатель имеет наибольшую частоту. Необходима наглядность, чтобы лучше представить моду и виды средних величин в статистике. Таблица, которую мы рассмотрим ниже, представляет собой часть задачи, условие которой такое: Определите моду по данным рабочих цеха о дневной выработке. | Дневная выработка, шт. | 32-36 | 36-40 | 40-44 | 44-48 | | Численность рабочих, человек | 8 | 20 | 24 | 19 |
В нашем случае модальный интервал - это отрезок показателя дневной выработки с наибольшей численностью человек, то есть 40-44. Его нижняя граница - 44. А теперь обсудим, как же вычислить эту самую моду. Формула не очень сложная и записать её можно так: M= x1+ n*(fM-fM-1)/((fM-fM-1)+(fM-fM+1)). Здесь fM - частота модального интервала, fM-1 - частота интервала перед модальным (в нашем случае это 36-40), fM+1 - частота интервала после модального (для нас - 44-48), n - величина интервала (то есть разность между нижней и верхней границей)? x1 - значение нижней границы (в примере это 40). Зная все эти данные, мы можем смело вычислить моду на количество дневной выработки: M=40 +4*(24-20)/((24-20)+(24-19)) = 40 + 16/9 = 41,(7). Структурные средние величины статистика. МедианаРазберём ещё такой вид структурных величин, как медиана. Подробно на нём мы не будем останавливаться, расскажем лишь о различиях с предыдущим типом. В геометрии медиана делит угол пополам. Не зря в статистике этот вид средней величины так назвали. Если ранжировать ряд (к примеру, по численности населения того или иного веса в порядке возрастания численности), то медианой будет такое значение, которое делит этот ряд на две части, равные по численности. Другие виды средних величин в статистикеСтруктурные типы вкупе со степенными дают далеко не всё, что требуется для расчётов в различных областях. Выделяют и другие типы этих данных. Таким образом, бывают средние взвешенные. Этот тип применяется тогда, когда числа в ряде имеют разный "вещественный вес". Это можно объяснить на простом примере. Возьмём автомобиль. Он движется с разной скоростью в разные промежутки времени. При этом друг от друга отличаются и значения этих временных отрезков, и значения скоростей. Так вот, эти промежутки и будут являться вещественными весами. Взвешенными можно сделать любой вид степенных средних. В теплотехнике также применяется ещё один вид средних величин - среднее логарифмическое. Оно выражается достаточно сложной формулой, приводить которую мы не будем. 
Где это применяется?Статистика - наука, не привязанная к какой-либо одной сфере. Хоть и создана она была как часть социально-экономической сферы, но сегодня её методы и законы применяются в физике, химии, и биологии. Обладая знаниями в этой области, мы может легко определять тренды общества и вовремя предотвращать угрозы. Часто мы слышим фразы "угрожающая статистика", и это не пустые слова. Эта наука рассказывает нам о нас самих, и при должном её изучении способна предупредить о том, что может произойти. 
Как связаны виды средних величин в статистике?Соотношения между ними не всегда существуют, вот, например, структурные виды между собой не связаны никакими формулами. Но со степенными всё гораздо интереснее. Например, существует такое свойство: среднее арифметическое двух чисел всегда больше или равно их среднему геометрическому. Математически можно записать так: (a+b)/2 >= (a*b)1/2. Доказывается неравенство переносом правой части влево и дальнейшей группировкой. В итоге получаем разность корней, возведённую в квадрат. А так как любое число в квадрате положительное, соответственно, неравенство становится верным. Помимо этого есть более общее соотношение величин. Выясняется, что среднее гармоническое всегда меньше среднего геометрического, которое меньше среднего арифметического. А последнее оказывается, в свою очередь, меньше среднего квадратичного. Можете самостоятельно проверить правильность этих соотношений хотя бы на примере двух чисел - 10 и 6. 
Что в этом интересного?Интересно то, что виды средних величин в статистике, которые, казалось бы, показывают просто какой-то средний уровень, на самом деле могут сказать знающему человеку гораздо больше. Когда мы смотрим новости, никто и не задумывается над смыслом этих цифр и тем, как вообще их находить. Что можно ещё почитать?Для дальнейшего освоения темы мы рекомендуем прочитать (или прослушать) курс лекций по статистике и высшей математике. Ведь в этой статье мы рассказали лишь о крупинке того, что содержит в себе эта наука, и сама по себе она интереснее, чем кажется на первый взгляд. 
Как эти знания мне помогут?Возможно, они и пригодятся вам в жизни. Но если вам интересна сущность общественных явлений, их механизм и влияние на вашу жизнь, то статистика поможет вам глубже разобраться в этих вопросах. Вообще, она может описать практически любую сторону нашей жизни, если в её распоряжении имеются соответствующие данные. Ну а то, откуда и как добывается информация для анализа - тема отдельной статьи. ЗаключениеТеперь мы знаем, что бывают разные виды средних величин в статистике: степенные и структурные. Разобрались в способах их вычисления и в том, где и как это можно применить. fb.ru 2. виды средних величин - стр.6 2. Виды средних величин В статистической обработке материала возникают различные задачи, которые необходимо решать, и поэтому в статистической практике используются различные средние величины. Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая. Для того чтобы применить одну из вышеперечисленных видов средней, необходимо проанализировать изучаемую совокупность, определить материальное содержание изучаемого явления, все это делается на основе выводов, полученных из принципа осмысленности результатов при взвешивании или суммировании. В изучении средних величин применяются следующие показатели и обозначения. Признак, по которому находится средняя, называется осредняемым признаком и обозначается х; величина осредняемого признака у любой единицы статистической совокупности называют индивидуальным его значением, или вариантами, и обозначают как x 1, х 2, x 3,… х п; частота – это повторяемость индивидуальных значений признака, обозначается буквой f. Средняя арифметическая Один из наиболее распространенных видов средней – средняя арифметическая, которая исчисляется тогда, когда объем ос–редняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. Для вычисления средней арифметической величины сумму всех уровней признака делят на их число. Если некоторые варианты встречаются несколько раз, то сумму уровней признака можно получить умножением каждого уровня на соответствующее число единиц совокупности с последующим сложением полученных произведений, исчисленная таким образом средняя арифметическая называется средней арифметической взвешенной. Формула средней арифметической взвешенной выглядит следующим образом: гдехi – варианты, fi – частоты или веса. Взвешенная средняя величина должна употребляться во всех случаях, когда варианты имеют различную численность. Арифметическая средняя как бы распределяет поровну между отдельными объектами общую величину признака, в действительности варьирующуюся у каждого из них. Вычисление средних величин производят по данным, сгруппированным в виде интервальных рядов распределения, когда варианты признака, из которых исчисляется средняя, представлены в виде интервалов (от – до). Свойства средней арифметической: 1) средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин: Если хi = yi+zi, то Данное свойство показывает в каких случаях можно суммировать средние величины. 2) алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую сторону: Это правило демонстрирует, что средняя является равнодействующей. 3) если все варианты ряда увеличить или уменьшить на одно и тоже число α, то средняя увеличится или уменьшится на это же число α: 4) если все варианты ряда увеличить или уменьшить в А раз, то средняя также увеличится или уменьшится в А раз: 5) пятое свойство средней показывает нам, что она не зависит от размеров весов, но зависит от соотношения между ними. В качестве весов могут быть взяты не только относительные, но и абсолютные величины. Если все частоты ряда разделить или умножить на одно и тоже число d, то средняя не изменится. Средняя гармоническая. Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов и частот, т. е. значения х и f. Допустим, известны индивидуальные значения признака х и произведения х/, а частоты f неизвестны, тогда, чтобы рассчитать среднюю, обозначим произведение = х/; откуда: Далее преобразуем формулу средней арифметической так, чтобы по существующим данным хи m исчислить среднюю. Выразив в формуле средней арифметической / через х и m, получим: Средняя в этой форме называется средней гармонической взвешенной и обозначается х гарм. взв. Соответственно, средняя гармоническая тождественна средней арифметической. Она применима, когда неизвестны действительные веса f, а известно произведение fх = z Когда произведения fх одинаковы или равны единицы (m = 1) применяется средняя гармоническая простая, вычисляемая по формуле: где х – отдельные варианты; n – число. Средняя геометрическая Если имеется n коэффициентов роста, то формула среднего коэффициента: Это формула средней геометрической. Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего. Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д. Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число. Средняя квадратическая взвешенная равна: 3. Структурные средние величины. Мода и медиана Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана. Мода (Мо) – чаще всего встречающийся вариант. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений. Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой. где хо – нижняя граница модального интервала; h – величина модального интервала; fm – частота модального интервала; fт—1 – частота интервала, предшествующего модальному; fm+1 – частота интервала, следующего за модальным. Мода зависит от величины групп, от точного положения границ групп. Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя). Медиана (Me – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие. Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних. Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал: где хме– нижняя граница медианного интервала; iMe – величина медианного интервала; f/2 – полусумма частот ряда; SMe—1 – сумма накопленных частот, предшествующих медианному интервалу; fMe – частота медианного интервала. Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности. ЛЕКЦИЯ № 8. Показатели вариации 1. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по–разному сочетаются в каждом отдельном случае. Колебания отдельных значений характеризуют показатели вариации. Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую. Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Абсолютные и средние показатели вариации и способы их расчета Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (х мах ) и наименьшим (х т щ) значениями вариантов: R = Xmax—Xmin. Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений, которое учитывает различия всех единиц изучаемой статистической совокупности. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней без учета знака этих отклонений: На практике меру вариации более объективно отражает показатель дисперсии ( 2 – средний квадрат отклонений), определяемый как средняя из отклонений, возведенных в квадрат (х – х1)2 : Корень квадратный из дисперсии 2 среднего квадрата отклонений представляет собой среднее квадратическое отклонение σ2 и σ– общепринятые меры вариации признака. Среднее квадратическое отклонение – это мерило надежности средней. Свойства дисперсии (доказываемые в математической статистике), которые позволяют упростить расчеты: 1) если из всех значений вариант отнять какое–то постоянное число А2 , то средний квадрат отклонений от этого не изменится; 2) если все значения вариант разделить на какое–то постоянное число А, то средний квадрат отклонений уменьшится от этого в А2 раз, а среднее квадратическое отклонение – в А раз 3) если исчислить средний квадрат отклонений от любой величины А, которая в той или иной степени отличается от средней арифметической х, то он всегда будет больше среднего квадрата отклонений σ2 , исчисленного от средней арифметической. Показатели относительного рассеивания Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах, которые позволяют сравнивать характер рассеивания в различных распределениях. Расчет показателей меры относительного рассеивания осуществляют отношением абсолютного показателя рассеивания к средней арифметической и умножают на 100%. Виды дисперсий и закон сложения дисперсий При помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку–фактору, можно определить три показателя колеблемости признака в совокупности: общую дисперсию, межгрупповую дисперсию и среднюю из внут–ригрупповых дисперсий. Общая дисперсия характеризует вариацию признака, зависящую от всех условий в изучаемой статистической совокупности. Исчисляется общая дисперсия по формуле: где х0 – общая средняя для всей изучаемой совокупности. 2. Характеристика закономерности рядов распределения С помощью рядов распределения решается важнейшая задача статистики – характеристика и измерение показателей колеблемости для варьирующих признаков. В вариационных рядах существует определенная связь в изменении частот и значений варьирующего признака: с увеличением варьирующего признака величина частот вначале возрастает до определенной величины, а затем уменьшается. Такого рода изменения называются закономерностями распределения. Положение кривой распределения на оси абсцисс и ее рассеивание являются двумя наиболее существенными свойствами кривой. Важные свойства кривой распределения – это степень ее асимметрии, высоко–или низковершинность, которые в совокупности характеризуют форму или тип кривой распределения. Важная задача – это определение формы кривой, так как статистический материал в обычных условиях дает по определенному признаку характерную, типичную для него кривую распределения. Всякое искажение формы кривой – это нарушение или изменение нормальных условий возникновения материала: появление двухвершинной или асимметричной кривой говорит о разнотипном составе совокупности и о необходимости перегруппировки данных в целях выделения более однородных групп. Характер общего распределения предполагает оценку степени его однородности и вычисление показателей асимметрии и эксцесса. Симметричным называют распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая мода и медиана равны между собой. Простейший показатель асимметрии основан на соотношении показателей центра распределения. Наиболее точным и распространенным является показатель основанный на определении центрального момента третьего порядка. Общим является нормальное распределение, которое может быть представлено графически в виде симметричной куполообразной кривой. В сущности, распределения редко бывают точно асимметричны, поэтому нормальная кривая представляет собой идеализированную форму распределения. Куполообразная форма кривой показывает, что большинство значений концентрируется вокруг центра измерения, и в действительно симметричном одновершинном распределении средняя, мода и медиана совпадут. Закон нормального распределения предполагает, что отклонение от среднего значения является результатом большого количества мелких отклонений, что позитивные и негативные отклонения равновероятны и что наиболее вероятным значением всех в равной мере надежных измерений является их арифметическая средняя. Общие условия вариации признака отражены в характере и типе закономерностей распределения: сущность явления и те его свойства и условия, которые определяют изменчивость варьирующего признака. Теоретической кривой распределения называют кривую распределения, которая выражает общую закономерность данного типа. Огромное значение в теории выборочного метода имеет нормальная кривая, так как стандартные средние отклонения, рассчитанные по случайным выборкам, тяготеют к нормальным в случае больших размеров выборок, если даже совокупность не является нормально распределенной. В кривой нормального распределения отражается закономерность, которая возникает при взаимодействии множества случайных причин. Для симметричных распределений рассчитывается показатель эксцесса (островершинности).Т. Б. Линдбергом предложен такой показатель: Ех = n – 38,9, где п – доля (%) количества вариантов, лежащих в интервале, равном половине среднего квадратического отклонения в ту и другую сторону от х. Эксцесс – выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Оценка показателей асимметрии и эксцесса дает возможность сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения. ЛЕКЦИЯ № 9. Выборочное наблюдение 1. Определение выборочного наблюдения Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным. Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности по обследованной ее части. Выборочное наблюдение – это метод статистического исследования, при котором обобщающие показатели совокупности устанавливаются только по отдельно взятой части на основе положений случайного отбора. При выборочном методе изучению подвергается только некоторая часть изучаемой совокупности, при этом подлежащая изучению статистическая совокупность называется генеральной совокупностью. Выборочной совокупностью или просто выборкой можно называть отобранную из генеральной совокупности часть единиц, которая будет подвергаться статистическому исследованию. Значение выборочного метода: при минимальной численности исследуемых единиц проведение статистического исследования будет происходить в более короткие промежутки времени и с наименьшими затратами средств и труда. В генеральной совокупности доля единиц, которая обладает изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака – это генеральная средняя (обозначается х). В выборочной совокупности долю изучаемого признака называют выборочной долей, или частью (обозначается w), средняя величина в выборке – это выборочная средняя. Если в период обследования будут соблюдены все правила его научной организации, то выборочный метод даст довольно точны результаты, и поэтому данный метод целесообразно применять для проверки данных сплошного наблюдения. Этот метод получил широкое распространение в государственной и вневедомственной статистике, потому что при исследовании минимальной численности изучаемых единиц позволяет тщательно и точно провести исследование. Изучаемая статистическая совокупность состоит из единиц с варьирующими признаками. Состав выборочной совокупности может отличаться от состава генеральной совокупности, это расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки. Ошибки, свойственные выборочному наблюдению, характеризуют размер расхождения между данными выборочного наблюдения и всей совокупности. Ошибки, возникающие в ходе выборочного наблюдения, называются ошибками репрезентативности и делятся на случайные и систематические. Если выборочная совокупность недостаточно точно воспроизводит всю совокупность из–за несплошного характера наблюдения, то это называют случайными ошибками, и их размеры определяются с достаточной точностью на основании закона больших чисел и теории вероятностей. Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения. refdb.ru древний закон средних величин — advODKA.com| 1 |
mail.ru |
190 000 |
да |
8 |
да |
7 228 974 |
15 700 000 |
Ответы@Mail.Ru: ..."древний закон средних величин"? |
Отменить Со Средние величины тесно связан закон больших чисел (см. Больших чисел закон) . При наличии случайного элемента в индивидуальных значениях ... Средние величины - Словари и Энциклопедии на... |
| 2 |
jurnalpravil.ru |
0 |
— |
0 |
— |
79 |
10 |
Home | онлайн журнал историй - ...основан на "Законах... |
Если же вы выбросите кубик сто пятьдесят раз, то в силу вступит закон средней величины. Чем чаще вы будите бросать кубик, тем вероятнее, что все числа выпадут одинаковое количество раз. |
| 3 |
osoznannie-snovidenya.ru |
60 |
— |
1 |
да |
2 052 |
1 200 |
Закон Средних Величин | Всё про сны и сновидения |
Закон Средних Величин применительно к Сетевому М кетингу гласит: "Из каждых десяти человек, которым вы черпывающим образом рассказали о предлагаемой им можности заняться бизнесом... |
| 4 |
naturnike.ru |
60 |
— |
1 |
— |
3 978 |
980 |
Самовнушение! Сильные слова! Подействует на каждого!... |
Я буду помнить древний закон средних величин и использовать его себе во благо. Каждое, услышанное мною "нет", приближает меня к "да". Каждый встречный хмурый взгляд готовит меня к встрече с улыбкой. |
| 5 |
mql4.com |
190 |
да |
4 |
— |
2 707 |
660 |
Закон Средних Чисел - MQL4 форум |
Закон Средних Чисел. К списку тем | 1 2 3 4 Авторизуйтесь или зарегистрируйтесь, чтобы создать новую тему. ... А что если испытания проводятся в нестационарной среде? Оказывается, здесь действует Закон Средних Чисел. |
| 6 |
krmagazine.ru |
0 |
да |
2 |
— |
1 090 |
20 |
Закон средних чисел или в чем секрет успешных продавцов |
Раздел для продавцов и безнесменов сферы торговли. Новости и информация в мире бизнеса торговли., Закон средних чисел или в чем секрет успешных продавцов. |
| 7 |
yspu.org |
1 200 |
да |
5 |
да |
18 343 |
3 300 |
...если каждая случайная величина задана законом... |
Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным. |
| 8 |
wikipedia.org |
97 000 |
да |
9 |
да |
3 695 401 |
18 800 000 |
Закон больших чисел — Википедия |
Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию)... |
| 9 |
древняя.рф |
0 |
— |
0 |
— |
1 007 |
90 |
Средние величины | Закон больших чисел — Википедия |
Тайны древних. Средние величины. индивидуальный рабочий, Петр или Павел, более или менее отклоняется от среднего рабочего. ... Со Средние величины тесно связан закон больших чисел (см. Больших чисел закон). |
| 10 |
szuap.ru |
40 |
— |
1 |
— |
1 828 |
90 |
Древний закон средних величин - знакомим... |
Я буду помнить древний закон средних величин и использовать его себе во благо. Существуют различные типы Средние величины (см. Средние). Эту закономерность мы называем законом средних величин, но не всякий такой закон .... |
| 11 |
carbon26.ru |
0 |
— |
1 |
— |
454 |
0 |
Древний закон средних величин - Актуальные документы |
Архив drevniy-zakon-srednih-velichin.zip загружается на всех Windows которые имеют винзип или винрар. ... Теги: Как работает закон средней величины, Древний закон средних величин - абсолютно новое. |
| 12 |
allbest.ru |
3 000 |
да |
6 |
— |
833 039 |
146 000 |
Средняя величина |
Средняя величина. Понятие средней величины, условия применения. Виды средних и способы их вычисления. ... Коэффициенты использования рабочего времени. Закон распределения случайной величины. Функция плотности. |
| 13 |
e-ng.ru |
80 |
— |
3 |
— |
34 570 |
6 400 |
Закон больших чисел - Экономика и экономическая теория |
Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными... |
| 14 |
lenkovo.ru |
0 |
— |
0 |
— |
2 452 |
80 |
Древний закон средних величин - Все интересное... |
Я буду помнить древний закон средних величин и использовать его себе во благо. Имя найденного файла: древний закон средних величин.doc Добавлено: 18.01.2012 Скорость загрузки: 3457 Кб/сек. |
| 15 |
ligasb.ru |
30 |
— |
1 |
— |
242 |
0 |
Древний закон средних величин - Обновленные узоры. |
Галлей – знаменитый английский астроном выдвинул идею закона больших .... Скачать книгу: Гальтон, Ф. Я буду помнить древний закон средних величин и использовать его себе во благо. |
| 16 |
academic.ru |
5 000 |
да |
7 |
да |
1 347 750 |
2 850 000 |
Больших чисел закон |
в тенденции, в среднем, но не в непосредственной действительности» (там же, т. 39, с. 355). Отклонения множества цен от стоимости Маркс трактует как форму проявления закона стоимости: «...возможность отклонения цены от величины стоимости... |
| 17 |
studfiles.ru |
275 |
да |
3 |
— |
356 981 |
39 000 |
...(В. Вольтерра) (ЗАКОН НАРУШЕНИЯ СРЕДНИХ ВЕЛИЧИН) |
Закон Копа и Денера объясняет массовое вымирание организмов (напр., древнейших пресмыкающихся) весьма незначительными естественными ... ЗАКОНЫ СИСТЕМЫ «ХИЩНИК ЖЕРТВА» (В. Вольтерра) (ЗАКОН НАРУШЕНИЯ СРЕДНИХ ВЕЛИЧИН) |
| 18 |
exponenta.ru |
1 500 |
да |
5 |
да |
29 982 |
7 700 |
Теория вероятностей Введение |
Числовые характеристики двумерных случайных величин. Закон больших чисел. ... Средним гармоническим случайной величины, принимающей положительные значения, называется величина . |
| 19 |
grandars.ru |
550 |
— |
3 |
— |
205 070 |
213 000 |
Средние величины |
Сущность и виды средних величин. Степенные средние: арифметическая, гармоническая, геометрическая, квадратическая. |
| 20 |
ekonomstat.ru |
0 |
— |
0 |
— |
4 159 |
1 200 |
Средние величины - Курс лекций по теории статистики |
Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным. |
advodka.com
|
