Старинные способы умножения. Древние методы счета

Старинные способы умножения

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (410,9 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

“Счёт и вычисления – основа порядка в голове”. Песталоцци

Цель:

• Познакомиться со старинными приемами умножения.
• Расширить знания по различным приемам умножения.
• Научиться выполнять действия с натуральными числами, используя старинные способы умножения .

Содержание.

1. Старинный способ умножение на 9 на пальцах
2. Умножение методом Ферроля.
3. Японский способ умножения.
4. Итальянский способ умножения (“Сеткой”)
5. Русский способ умножения.
6. Индийский способ умножения.

Ход занятия

Актуальность использования приемов быстрого счета.

В современной жизни каждому человеку часто приходится выполнять огромное количество расчётов и вычислений. Поэтому цель моей работы – показать лёгкие, быстрые и точные методы счёта, которые не только помогут вам во время каких-либо расчётах, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта. Основополагающим элементом вычислительной культуры являются сознательные и прочные вычислительные навыки. Проблема формирования вычислительной культуры актуальна для всего школьного курса математики, начиная с начальных классов, и требует не простого овладения вычислительными навыками, а использования их в различных ситуациях. Владение вычислительными умениями и навыками имеет большое значение для усвоения изучаемого материала, позволяет воспитывать ценные трудовые качества: ответственное отношение к своей работе, умение обнаруживать и исправлять допущенные в работе ошибки, аккуратное исполнение задания, творческое отношение к труду. Однако, в последнее время уровень вычислительных навыков, преобразований выражений имеет ярко выраженную тенденцию к снижению, учащиеся допускают массу ошибок при подсчетах, все чаще используют калькулятор, не мыслят рационально, что отрицательно сказывается на качестве обучения и уровне математических знаний учащихся в целом. Одной из составляющих вычислительной культуры является устный счёт, который имеет большое значение. Умение быстро и правильно произвести несложные вычисления “в уме” необходимо для каждого человека.

 Старинные способы умножения чисел.

1. Старинный способ умножение на 9 на пальцах

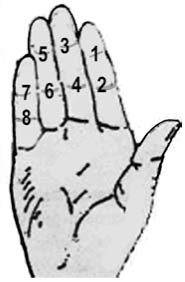
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

2. Умножение методом Ферроля.

Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.

Например: 12х14=168

а) 2х4=8, пишем 8

б) 1х4+2х1=6, пишем 6

в) 1х1=1, пишем 1.

3. Японский способ умножения

Такой прием напоминает умножение столбиком, но проводится довольно долго.

Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:

Этот рисунок состоит из 10 линий (количество может быть любым)

• Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
• А эти линии обозначают число 13 (1 линия, отступ, 3 линии)

Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом:

(пересечения на рисунке указаны точками)

Количество пересечений:

• Верхний левый край: 2
• Нижний левый край: 6
• Верхний правый: 4
• Нижний правый: 12

1) Пересечения в верхнем левом крае (2) – первое число ответа

2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа

3) Пересечения в нижнем правом крае (12) – третье число ответа.

Получается: 2; 10; 12.

Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.

3(2+1)1(0+1)2

Ответ: 312

4. Итальянский способ умножения (“Сеткой”)

В Италии, а также во многих странах Востока, этот способ приобрел большую известность.

Использование приема:

Например, умножим 6827 на 345.

1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.

2. Умножаем число каждого ряда последовательно на числа каждой колонки.

т.е.

• 6*3 = 18. Записываем 1 и 8
• 8*3 = 24. Записываем 2 и 4

Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.

(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)

3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.

Ответ: 2355315.

5. Русский способ умножения.

Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:

• 32 * 13 (32 делим на 2, а 13 умножаем на 2)
• 16 * 26 (16 делим на 2, а 26 умножаем на 2)
• 8 * 52 (и т.д.)
• 4 * 104
• 2 * 208
• 1 * 416 =416

Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение

Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, - гласит правило, - в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):

• 19*17
• 9*34
• 4 *68*
• 2 *136*
• 1 *272

Сложив незачеркнутые числа, получаем вполне правильный результат:

Ответ: 323.

6. Индийский способ умножения.

Такой способ умножения использовали в Древней Индии.

Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.

Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила:

• Правило 1. Единицы первого произведения следует писать в той же колонке, что и множитель, то есть в данном случае под 9.
• Правило 2. Последующее произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.

Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).

Затем складываем цифры в колонках и получаем ответ: 72956.

Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат.

Заключение

Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, “экономическую - ситуацию” в стране, погоду на “завтра”, описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора - “Всё есть число!”.

Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.

Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.

“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)

Литература.

1. Энциклопедия для детей. “T.23”. Универсальный энциклопедический словарь \ ред. коллегия: М. Аксёнова, Е.Журавлёва, Д.Люри и др. – М.: Мир энциклопедий Аванта +, Астрель, 2008. – 688 с.
2. Ожегов С. И. Словарь русского языка : ок. 57000 слов/ Под ред. чл. – корр. АНСИР Н.Ю. Шведовой. – 20 – е изд.– М. : Просвещение, 2000. – 1012 с.
3. Xочу всё знать! Большая иллюстрированная энциклопедия интеллекта / Пер. с англ. А. Зыковой, К. Малькова, О.Озёровой. – М.: Изд-во ЭКМО, 2006. – 440 с.
4. Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка 5-6 кл./ О.С.Шейнина, Г.М. Соловьева – М.: Изд-во НЦЭНАС, 2007. – 208 с.
5. Кордемский Б. А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.
6. Минских Е. М. “От игры к знаниям”, М., “Просвещение” 1982г.
7. Свечников А. А. Числа, фигуры, задачи М., Просвещение, 1977г.
8. http://matsievsky. newmail. ru/sys-schi/file15.htm
9. http://sch69.narod. ru/mod/1/6506/hystory. html

xn--i1abbnckbmcl9fb.xn--p1ai

"Как в древности люди обходились без электронных вычислителей"

Филиал МКОУ «Лебяжьевская СОШ» «Плосковская СОШ»

Исследовательская работа

по математике

Как в древности люди обходились без электронных вычислителей.

Выполнила:

Шаньгина Люба

учениц 10 класса

Руководитель:

Иванова Светлана

Александровна

Оглавление

Введение

Глава 1. История счета

Глава 2. Старинные приборы и их изучение

Заключение

Список литературы

Введение

Можно ли представить себе мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.

Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. В нашей работе предпочтение отдано стихии чисел и старинным приборам для их вычисления.

Сейчас, на этапе стремительного развития информатики и вычислительной техники, современные школьники не хотят утруждать себя счетом в уме. Поэтому мы сочли важным показать не только то, что сам процесс выполнения действия может быть интересным, но и как раньше люди обходились без электронных вычислителей.

Объектом исследования являются числа и вычислительные приборы

Предметом исследования выступает процесс вычисления и изучение приборов

Цель: изучить приёмы вычислений старинными приборами и экспериментальным путем выявить причину отказа от использования старинных приборов при обучении математике современных школьников.

Задачи:

- раскрыть историю возникновения приборов и феномен « Чудо - счётчиков»;

- описать старинные приборы и опытно-экспериментальным путем выявить трудности в их использовании;

-рассмотреть некоторые приборы и на конкретных примерах показать преимущества их использования.

Гипотеза: в старину говорили: « Вычисленье – мое мученье». Значит, раньше было сложно и трудно вычислять. Прост ли наш современный способ вычисления?

При работе над докладом я пользовалась следующими методами:

поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;

практический метод выполнения вычислений с применением старинных вычислительных приборов

анализ полученных в ходе исследования данных.

Актуальность данной темы заключается в том, что использование старинных вычислительных приборов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.

За простыми действиями вычисления скрываются тайны истории математики. Случайно услышанные слова «Абак», «Счеты»,«Соробан»,«Арифмометр»,«Суаньпань» заинтриговали. Захотелось узнать эти и другие приборы вычисления, сравнить их с нашими сегодняшними.

Для того чтобы выяснить, знают ли современные школьники другие приборы вычисления, кроме калькуляторов и хотели бы узнать новые , был проведен устный опрос. Было опрошено 20 учащиеся. Этот опрос показал, что современные школьники не знают других приборов вычисления кроме калькулятора, так как редко обращаются к материалу, находящемуся за пределами школьной программы.

Результат анкетирования:

Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку?

А умеете ли вы вычислять без помощи калькулятора?

Знаете ли вы какие- либо вычислительные приборы, кроме калькулятора?

А хотелось ли вам узнать о них.?

Я побывала в сельском магазине и спросила продавца, который уже много лет работает в магазине как ей удобно работать на калькуляторе или на счетах, она ответила: «Я перемножаю числа на калькуляторе, а складываю на счетах, мне удобнее работать на счетах так как я не сбиваюсь при счете на счетах да и покупатель видит на сколько он набрал товару, а кто не понимает как смотреть по счетам, то я и говорю мне не сложно. Сейчас молодежь которая работает в магазинах больше всего пользуются калькуляторами и вычислительными машинками, так как сейчас в наше время очень мало осталось старинных вычислительных приборов, но мне все же удобнее работать так».

Глава 1. История счёта

1.1. Как возникли числа

Подсчитывать предметы люди научились ещё в древнем каменном веке - палеолите, десятки тысяч лет назад. Как это происходило? Сначала люди лишь на глаз сравнивали разные количества одинаковых предметов. Они могли определить, в какой из двух куч больше плодов, в каком стаде больше оленей и т. д. Если одно племя меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. Достаточно было положить рядом с каждой рыбой по ножу, чтобы обмен между племенами состоялся.

Чтобы с успехом заниматься сельским хозяйством, понадобились арифметические знания. Без подсчета дней трудно было определить, когда надо засевать поля, когда начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары.И вот более восьми тысяч лет назад древние пастухи стали делать из глины кружки - по одному на каждую овцу Чтобы узнать, не пропала ли за день хоть одна овца, пастух откладывал в сторону по кружку каждый раз, когда очередное животное заходило в загон. И только убедившись, что овец вернулось столько же, сколько было кружков, он спокойно шел спать. Но в его стаде были не только овцы - он пас и коров, и коз, и ослов. Поэтому пришлось делась из глины и другие фигурки. А земледельцы с помощью глиняных фигурок вели учет собранного урожая, отмечая, сколько мешков зерна положено в амбар, сколько кувшинов масла выжато из оливок, сколько соткано кусков льняного полотна. Если овцы приносили приплод, пастух прибавлял к кружкам новые, а если часть овец шла на мясо, несколько кружков приходилось убирать. Так, еще не умея считать, занимались древние люди арифметикой.

Затем в человеческом языке появились числительные, и люди смогли называть число предметов, животных, дней. Обычно таких числительных было мало. Например, у племени реки Муррей в Австралии было два простых числительных: энэа (1) и петчевал (2). Другие числа они выражали составными числительными: 3= «петчевал-энэа», 4 «петчевал-петчевал» и т. д. Ещё одно австралийское племя – камилороев имело простые числительные мал (1), булан (2), гулиба (3) . И здесь другие числа получались сложением меньше: 4= «булан – булан», 5= «булан – гулиба», 6= « гулиба – гулиба» и т. д.

У многих народов название числа зависело от под считываемых предметов. Если жители островов Фиджи считали лодки, то число 10 называли « боло»; если они считали кокосовые орехи, то число 10 называли «каро». Точно так же поступали живущие на Сахалине и берегах Амура нивхи. Ещё в прошлом веке одно и то же число они называли разными словами, если считали людей, рыб, лодки, сети, звёзды, палки.

Мы и сейчас используем разные неопределённые числительные со значением «много»: «толпа», «стадо», «стая», «куча», «пучок» и другие.

С развитием производства и торгового обмена люди стали лучше понимать, что общего у трёх лодок и трёх топоров, десяти стрел и десяти орехов. Племена часто вели обмен «предмет за предмет»; к примеру, обменивали 5 съедобных кореньев на 5 рыб. Становилось ясно, что 5 одно и то же и для кореньев, и для рыб; значит, и называть его можно одним словом.

Постепенно люди начали использовать для счёта камешки, палочки, части собственного тела. Вот как известный русский учёный Н. Н. Миклуха - Маклай описывал счёт папуасов: «Папуас загибает один за другим пальцы руки, причём издаёт определённый звук, например «бе, бе, бе..». Досчитав до пяти, он говорит: «Ибон-бе» (рука). Затем он загибает пальцы другой руки, снова повторяя «бе, бе..», пока не дойдёт до «ибон-али» (две руки). Затем он идёт дальше, приговаривая «бе, бе…», пока не дойдёт до «самба-бе» (одна нога) и «самба-али» (две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого».

Похожие способы счёта применяли и другие народы. Так возникли нумерации, основанные на счёте пятёрками, десятками, двадцатками.

До сих пор мы рассказывали об устном счёте. А как записывали числа? Поначалу, ещё до возникновения письменности, использовали зарубки на палках, насечки на костях, узелки на верёвках. Найденная волчья кость в Дольни - Вестонице (Чехословакия), имела 55 насечек, сделанных более 25000 лет назад.

Когда появилась письменность, появились и цифры для записи чисел. Сначала цифры напоминали зарубки на палках: в Египте и Вавилоне, в Этрурии и Финики, в Индии и Китае небольшие числа записывали палочками или чёрточками. Например, число 5 записывали пятью палочками. Индейцы астеки и майя вместо палочек использовали точки. Затем появились специальные знаки для некоторых чисел, таких, как 5 и 10 .

В то время почти все нумерации были не позиционными, а похожими на римскую нумерацию. Лишь одна вавилонская шестидесятеричная нумерация была позиционной. Но и в ней долго не было нуля, а также запятой, отделяющей целую часть от дробной. Поэтому одна и та же цифра могла означать и 1, и 60, и 3600. Угадывать значение числа приходилось по смыслу задачи.

За несколько столетий до новой эры изобрели новый способ записи чисел, при котором цифрами служили буквы обычного алфавита. Первые 9 букв обозначали числа десятки 10, 20,…, 90, а ещё 9 букв обозначали сотни. Такой алфавитной нумерацией пользовались до 17 в. Чтобы отличить «настоящие» буквы от чисел, над буквами- числами ставили чёрточку (на Руси эта чёрточка называлась «титло»).

Во всех этих нумерациях было очень трудно выполнить арифметические действия. Поэтому изобретение в 6 в. индийцами десятичной позиционной нумерации по праву считается одним из крупнейших достижений человечества. Индийская нумерация и индийские цифры стали известны в Европе от арабов, и обычно их называют арабскими.

нумерации, а дробную – в шестидесятеричной. Но в начале 15 в. самаркандский математик и астроном аль - Каши стал употреблять в вычислениях десятичные дроби.

Числа, с которыми мы работаем с положительными и отрицательными числами. Но, оказывается, что это не все числа, которые используют в математике и других науках. И узнать о них можно не дожидаясь старшей школы, а гораздо раньше, если изучать историю возникновения чисел в математике.

1.2 « Чудо - счётчики»

Он все понимает с полуслова и тут же формулирует вывод, к которому обычный человек, может быть, придет путем долгих и тягостных раздумий. Книги он поглощает с невероятной скоростью, а на первом месте в его шорт-листе бестселлеров — учебник по занимательной математике. В момент решения самых трудных и необычных задач в его глазах горит огонь вдохновения. Просьбы сходить в магазин или помыть посуду остаются без внимания либо выполняются с большим недовольством. Самая лучшая награда — это поход в лекторий, а самый ценный подарок — книга. Он максимально практичен и в своих поступках в основном подчиняется рассудку и логике. Он холодно относится к окружающим его людям и предпочтет катанию на роликах шахматную партию с компьютером. Будучи ребенком, он не по годам осознает собственные недостатки, отличается повышенной эмоциональной устойчивостью и приспособляемостью к внешним обстоятельствам.

За порогом сознания чудо - счетоводы, способные без калькулятора совершать невообразимо сложные арифметические действия, обладают уникальными особенностями памяти, отличающей их от других людей. Как правило, кроме огромных линеек формул и вычислений, эти люди (ученые их называют мнемониками — от греческого слова mnemonika, означающего "искусство запоминания") держат в голове списки адресов не только друзей, но и случайных знакомых, а также многочисленных организаций, где им когда-то приходилось бывать.

В лаборатории НИИ психотехнологии, где решили исследовать феномен, провели такой эксперимент. Пригласили уникума — сотрудника Центрального государственного архива Санкт-Петербурга Александра Н. Ему предлагали для запоминания различные слова и цифры. Он должен был их повторять. За каких-то пару минут он мог зафиксировать в памяти до семидесяти элементов. Десятки слов и цифр буквально "загрузили" в память Александра. Когда количество элементов перевалило за две сотни, решили проверить его возможности. К удивлению участников эксперимента, мегапамять не дала ни одного сбоя. С секунду пошевелив губами, он с поразительной точностью, словно читая, начал воспроизводить весь ряд элементов.

Еще, например, один учёный – исследователь провёл эксперимент с мадмуазель Осака. Испытуемую попросили возвести в квадрат 97, получить десятую степень того числа. Она это сделала моментально.

В Ванском районе западной Грузии живет Арон Чикашвили. Он быстро и точно производит в уме сложнейшие вычисления. Как-то друзья решили проверить возможности «чудо-счётчика». Задание было сложным: сколько слов и букв скажет диктор, комментирующий второй тайм футбольного матча «Спартак» (Москва) - «Динамо» (Тбилиси). Одновременно был включен магнитофон. Ответ последовал, как только диктор сказал последнее слово: 17427 букв, 1835 слов. На проверку ушло ….5 часов. Ответ оказался правильным.

Рассказывают, что отец Гаусса обычно платил свом рабочим в конце недели, прибавляя к каждому дневному заработку за сверхурочные часы. Однажды после того, как Гаусс-отец закончил расчеты, следивший за операциями отца ребёнок, которому было три года, воскликнул: « Папа, подсчёт не верен! Вот такая должна быть сумма». Вычисления повторили и с удивлением убедились, что малыш указал правильную сумму.

Интересно, что многие «чудо-счётчики» не имеют понятия вообще, как они считают. « Считаем, и всё! А как считаем, Бог его знает». Некоторые «счётчики» были совсем необразованными людьми. Англичанин Бакстон, «счётчик-виртуоз», так никогда и не научился читать; американский «негр-счётчик» Томас Фаллер умер неграмотным в возрасте 80-ти лет.

Проводились соревнования в институте кибернетики Украинской академии наук. В соревновании участвовали молодой «счётчик-феномен» Игорь Шелушков и ЭВМ «Мир». Машина за несколько секунд сделала множество сложных математических операций. Победителем в этом соревновании вышел Игорь Шелушков.

В Сиднейском университете в Индии тоже проходили соревнования человека и машины. Шакунтала Деви тоже несколько опередила ЭВМ.

Большенство таких людей обладает прекрасной памятью и имеют дарование. Но некоторые из них никакими способностями к математике не обладают. Они знают секрет! А секрет этот в том, что они хорошо усвоили приемы быстрого счёта, запомнили несколько специальных формул. Но бельгийский служащий, который за 30 секунд по предложенному ему многозначному числу, полученному от умножения некоторого числа само на себя 47 раз, называет это число (извлекает корень 47-ой степени из многозначного числа), добился таких потрясающих успехов в счёте в результате многолетней тренировки.

Итак, многие «счётчики-феномены» пользуются особыми приемами быстрого счёта и специальными формулами. Значит, мы тоже можем пользоваться некоторыми из этих приёмов.

Глава II

Старинные приборы

В этой главе я хочу рассказать и познакомить обучающихся нашей школы, какие были раньше приборы, как люди на них считали и кем они были открыты .На пальцах считать удобно, только результат счета хранить нельзя. Не станешь же целый день ходить с загнутыми пальцами. И человек догадался — для счета можно использовать все, что попадется под руку. Камешки, палочки, косточки, веревки и так далее. Пасет пастух стадо овец. На поясе у него веревка, а на веревке столько узелков, сколько овец в стаде. Родился ягненок — пастух завязал еще один узелок. Утащили волки двух овец — развязал два узелка.

С развитием цивилизации появлялись различные приемы счета. Они были необходимы и сборщикам налогов, и купцам, и ремесленникам, и ростовщикам. Искусством счета владели немногие специально обученные люди — счетчики. Они использовали счетные инструменты — абаки. «Абак»

Простейший абак — это доска с прорезанными в ней желобами. Чтобы найти сумму двух чисел (например, 258 и 125), счетчик сначала обозначал на абаке первое слагаемое. Для этого он укладывал в нижнем желобе 8 камешков, в следующем желобе — 5 камешков и 2 камешка — в третьем желобе. Если в каком-то разряде в числе стоял нуль, то соответствующий желоб оставался пустым. Дальше счетчик добавлял в последний желоб к имеющимся там 8 камешкам еще 5, затем вынимал оттуда 10 (там оставалось 3) и 1 камешек добавлял во второй желоб. Потом добавлял во второй желоб еще 2 камешка и 1 камешек — в третий желоб. После этого камешки на доске показывали число 383.

Абаки использовались уже в V-IV веках до нашей эры. Их изготавливали из бронзы, камня, слоновой кости, цветного стекла. Слово «абак» имеет греческое происхождение и буквально означает «пыль», хотя его смысловое значение — «счетная доска». В чем тут дело? Ответ прост: изначально камешки раскладывали на совершенно ровной доске, а чтобы они не скатывались со своего первоначального положения, доска покрывалась тонким слоем песка или пыли. А от слова «камешек» (по латыни — «calculus») произошло название современного счетного прибора — «калькулятор».

Абак использовался и в Древней Греции, и в Древнем Риме, а затем и в Западной Европе вплоть до XVIII века. Он похож на знакомые вам счеты — косточки на встав¬ленных в рамку металлических спицах.

«Суаньпань»

«Соробан»

Соробан с представленным на нём числом 123456,789

Соробан «счётная доска») — японские счёты (абак). Происходят от китайского суаньпаня завезённого в Японию в Средние века В настоящее время соробан продолжает использоваться,несмотря на распространение практичных и доступных населению карманных калькуляторов.

Устройство

Соробан состоит из нечётного количества вертикально расположенных спиц. Каждая спица представляет собой цифру. Обычно их 13, но встречаются соробаны и с 21 23, 27 или даже с 31 спицей. Большее количество спиц позволяет набирать большие числа, или представлять сразу несколько чисел на одном соробане. На каждой спице нанизано по 5 костяшек, причём верхняя костяшка на каждой спице отделена от нижних рамкой Четыре нижние костяшки называются «земными», и каждая представляет собой единицу. Верхняя костяшка называется «небесной» и считается за пять «земных».

«Счеты»

Счеты – простейший вычислительный аппарат, который представляет собой счетные кольца, нанизанные на тонкие спицы. Обрамленные единой канвой, счеты заключают в себе всю систему чисел – единицы, десятки, сотни и т.д. На верхних рядах счет расположены целые числа, причем их значение уменьшается с каждой следующей спицей: от сотен тысяч к единицам. Под коротким рядом «костяшек» расположены дробные числа: от десятых до тысячных.

2Самыми простыми вычислениями на счетах являются сложение и вычитание. Числа набираются начиная с первого ряда целых: от 1 до 10. Следующий рад (на одну спицу вверх) – от 11 до 20 и т.д. Набирайте необходимое число, передвигая «костяшки» из соответствующего ряда справа налево. Когда один ряд на спице заполнится, воспользуйтесь числами большего значения – то есть одна «костяшка» верхнего ряда заменяет 10 «костяшек» нижнего. Складывая числа, добавляйте «костяшки» в соответствующие ряды. Чтобы посчитать окончательный результат, «спускайтесь» внизу вверх – миллионы, тысячи, сотни и т.д.

3Вычитание на счетах производится таким же способом, что и сложение, только в обратном порядке. То есть вычитая из одного числа другое, убирайте «костяшки» из соответствующих рядов. Таким образом, во время подсчета двигайтесь сверху вниз. Окончательную сумму вы узнаете, подсчитав кольца, оставшиеся в левой стороне счет.

4Для каждого числа умножение на счетах производится разными способами. Если вам нужно умножить на 2 или 3, замените это действие сложением, «плюсуя» число 2 или 3 раза соответственно. Умножение на 4 – это сложение (2*2).

5Чтобы умножить на 5, перенесите все косточки счет на одну линию вверх (то есть умножьте его на 10), затем делите число пополам в уме.

6Чтобы умножить число на 6, его нужно умножить на 5 описанным выше способом, затем к полученному результату прибавить число, которое было в начале вычислений.

7Чтобы умножить на 7, сначала умножьте число на 10, а затем от полученного значения отнимите умножаемое число три раза.

8Умножение на 8 или 9 заменяют умножением на 10, но без переноса 2х или 1й (при умножении на 8 и 9 соответственно) косточки наверх.

9Множители, следующие после 10, «раскладывают» на составляющие. Например, вам нужно умножить на 12 – вы раскладываете этот множитель на 10 и 2. Сложите число с самим собой (умножьте на 2), затем прибавьте к нему удесятеренное значение.

10Деление на счетах – процесс сложный и доступный только профессионалам. В прежние времена нужно было проходить специальное обучение, чтобы освоить деление.

«Арифмометр»

Арифмо́метр— «число», «счёт» и греч. Μέτρον — «мера», «измеритель») — настольная или портативная механическая вычислительная машина, предназначенная для точного умножения и деления, а также для сложения и вычитания. Механическая вычислительная машина, ведущая автоматическую запись обрабатываемых чисел и результатов на особой ленте — арифмограф[1].Настольная или портативная: Чаще всего арифмометры были настольные или «наколенные» (как современные ноутбуки), изредка встречались карманные модели (Curta). Этим они отличались от больших напольных вычислительных машин, таких как табуляторы (Т-5М) или механические компьютеры (Z-1, Разностная машина Чарльза Бэббиджа).Механическая: Числа вводятся в арифмометр, преобразуются и передаются пользователю (выводятся в окнах счётчиков или печатаются на ленте) с использованием только механических устройств. При этом арифмометр может использовать исключительно механический привод (то есть для работы на них надо постоянно крутить ручку. Этот примитивный вариант используется, например, в «Феликсе») или производить часть операций с использованием электромотора (Наиболее совершенные арифмометры — вычислительные автоматы, например «Facit CA1-13», почти при любой операции используют электромотор).Точное вычисление: Арифмометры являются цифровыми (а не аналоговыми, как например логарифмическая линейка) устройствами. Поэтому результат вычисления не зависит от погрешности считывания и является абсолютно точным.Умножение и деление: Арифмометры предназначались в первую очередь для умножения и деления. Поэтому почти у всех арифмометров есть устройство, отображающее количество сложений и вычитаний — счётчик оборотов (так как умножение и деление чаще всего реализовано как последовательное сложение и вычитание; подробнее — см. ниже).Сложение и вычитание: Арифмометры могут выполнять сложение и вычитание. Но на примитивных рычажных моделях (например, на арифмометре «Феликс») эти операции выполнялись очень медленно — быстрее, чем умножение и деление, но заметно медленнее, чем на простейших суммирующих машинах или даже вручную. Не программируемый. При работе на арифмометре порядок действий всегда задаётся вручную — непосредственно перед каждой операцией следует нажать соответствующую клавишу или повернуть соответствующий рычаг. Это особенность арифмометра не включается в определение, так как программируемых аналогов арифмометров практически не существовало.

«Палочки Непера»

Джон Непер ( 1550-1617) Шотландец Джон Непер в 1614-м году опубликовал «Описание удивительных таблиц логарифмов». Он обнаружил, что сумма логарифма числа а и б равна логарифму произведения этих числе. Поэтому действия умножения сводилось к простой операции сложения. Так же им разработан инструмент перемножения чисел – «Костяшки Непера». он состоял из набора сегментированных стерженьков, которые можно было располагать таким образом, что, складывая числа в прилегающих к друг другу сегментах, получали результат их умножения. В книге, изданной в 1617 году, шотландский ученый Джон Непер описал способ умножения с помощью палочек, который в дальнейшем получил название «Палочки Непера». В основу этого устройства лег принцип умножения решеткой,широко распространенный в XVII веке.

Для умножения решеткой использовалась таблица, содержащая столько столбцов, сколько разрядов у множимого, и столько строк, сколько разрядов у множителя. Над столбцами таблицы записывается множимое так, чтобы разряды числа находились каждый над своим столбцом. Справа от таблицы записывался множитель так, чтобы каждый разряд числа был напротив своей строки. При этом старший разряд записывался напротив верхней строки. В каждую ячейку таблицы записывался результат перемножения разряда множимого, находящегося над этой ячейкой, и разряда множителя, находящегося справа от этой ячейки. Причем для записи результата ячейка разделялась по диагонали на две части. В верхнюю часть записывался старший разряд результата, а в нижнюю – младший. Затем произведения суммировались по наклонным плоскостям справа налево. Полученная сумма и есть окончательный результат. Проиллюстрируем выше сказанное на примере 568 * 7: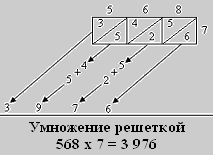

1. Чертим решетку с тремя столбцами и одной строкой, разделяем ячейки решетки на две части по диагонали.

2. Умножаем старший разряд множимого на множитель (5*7 = 35) и записываем результат в первую ячейку, причем разряд десяток записываем в верхнюю часть ячейки, а разряд единиц - в нижнюю.

3. Умножаем разряд десятков множимого на множитель (6*7 = 42) и записываем результат во вторую ячейку.

4. Умножаем разряд единиц множимого на множитель (8*7 = 56) и записываем результат в третью ячейку.

5. Суммируем строку решетки по наклонной плоскости справа налево. Суммирование по наклонной плоскости проводится поразрядно с переносом переполнения в старший разряд. Каждый разряд равен сумме чисел в прилегающих друг к другу треугольниках соседних ячеек. Полученная сумма - это результат умножения.

На рисунке слева приведен пример умножения с помощью решетки для многоразрядного множителя. Все действия аналогичны примеру с одноразрядным множителем, только несколько усложняется суммирование по наклонной плоскости.

Используя этот способ умножения, Джон Непер создал свой прибор – «Палочки Непера». Он представлял собой набор палочек, в который входила одна палочка с нанесенными на нее цифрами от 1 до 9 (указатель строк) и палочки с таблицей умножения всех чисел от 1 до 9 (разряды множимого). Сверху каждой такой палочки наносилось число от 1 до 9, а вдоль длины – результаты умножения этого числа на все числа от 1 до 9. По сути дела палочки Непера представляли собой решетку для умножения числа 123456789 на число 123456789, разрезанную на столбцы.

Заключение.

В начале нашей исследовательской работы мы поставили проблему – выяснить, почему ученики все чаще используют электронные приборы вычисления и познакомить с древними приборами. В ходе изучения литературы мы выяснили, что дети с появлением электронных приборов вычисления не хотят утруждать себя счетом в уме и просто не знаю старинных приборов вычисления. Мы узнали, какие в мире существовали приборы вычисления.

В ходе изучения специальной литературы, проведения наблюдений мы выяснили, что необходимо ввести в учебную часть те математические приборы вычисления, которые существовали в древности и научить детей на них работать.

Проведенные нами наблюдения помогли убедиться в правильности выдвинутой гипотезы: если раньше люди не могли и не умели считать, то им было труднее чем нам сейчас .

Практическая значимость данной работы заключается в том, что собранные материалы могут быть использованы учащимися и учителями для дополнительных занятий по математике.

Таким образом, задачи исследовательской работы решены, поставленная цель достигнута, выдвинутая проблема выяснена.

xn--j1ahfl.xn--p1ai

История развития вычислительной техники - ручной этап

Самым первым инструментом счета у древнего пещерного человека в верхнем палеолите, безусловно, были пальцы рук. Сама природа предоставила человеку этот универсальный счетный инструмент. У многих народов пальцы (или их суставы) при любых торговых операциях выполняли роль первого счетного устройства. Для большинства бытовых потребностей людей их помощи вполне хватало. К счету по пальцам рук восходят многие системы счисления, например пятеричная (одна рука), десятеричная (две руки), двадцатеричная (пальцы рук и ног), сорокаричная (суммарное число пальцев рук и ног у покупателя и продавца). У многих народов пальцы рук долгое время оставались инструментом счета и на наиболее высоких ступенях развития. Известные средневековые математики рекомендовали в качестве вспомогательного средства именно пальцевый счет, допускающий довольно эффективные системы счета. Однако в разных странах и в разные времена считали по-разному. Несмотря на то что у многих народов кисть руки является синонимом и фактической основой числительного "пять", у различных народов при пальцевом счете от одного до пяти указательный и большой пальцы могут иметь разные значения. У итальянцев при счете на пальцах рук большой палец обозначает цифру 1, а указательный - метит цифру 2; когда же считают американцы и англичане, указательный палец означает цифру 1, а средний - 2, в этом случае большой палец представляет цифру 5. А русские начинают счет на пальцах, первым загибая мизинец, и заканчивают большим пальцем, обозначающим цифру 5, при этом указательный палец сопоставлялся с цифрой 4. Но когда показывают количество, выставляют указательный палец, затем средний и безымянный. Средняя Европа Североевропейский пальцевой счет позволял показывать пальцами одной руки, складываемыми в различные комбинации, все числа от 1 до 100. Причем большим и указательным пальцами изображались десятки, остальными тремя - единицы. Например, число 30 получалось, когда большой и указательный пальцы левой руки были соединены в кольцо. Для того чтобы изобразить число 60, большой палец нужно согнуть и как бы склонить его перед указательным, нависающим над ним. Чтобы показать число 100, нужно было прижать выпрямленный большой палец снизу к указательному и отвести остальные три пальца в сторону. Россия В древнерусской нумерации единицы назывались "перстами", десятки - "суставами", а все остальные числа - "сочислениями". Счет парами вплоть до середины XVIII века всегда занимал важное место в жизни россиян, поскольку имел качественное происхождение - пара рук, ног, глаз и пр. Недаром говорили: "два сапога - пара", "двугривенный" и т.д. Четверичная система счета основана на "перстах" руки, не считая большого пальца. Большой - вовсе не "перст", он "палесъ"! - в этой системе счисления означал конец счета, то есть являлся эквивалентом нуля. Счет восьмерками также основан на пальцевом счете и, по сути, является сочетанием двоичной и четверичной систем. Элементы восьмеричной системы существовали на Руси еще в начале XX столетия. Это и восьмиконечный крест, который использовали староверы, и восьмиголосное церковное пение, и название русской питейной меры - "осьмушки", получаемой в результате последовательного троекратного деления пополам. В русской народной метрологии - это вообще деление какой-либо учетной нераздельной меры (например, куска пахотной земли, сажени или ведра вина) на части, соответствующие 1/2,1/4 и 1/8 долям. Пальцевой счет девятками является, пожалуй, самым распространенным русским народным способом умножения на пальцах с помощью так называемых девятериц - своеобразной таблицы 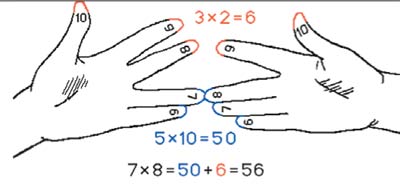умножения, обозначающей девятилетние сроки человеческой жизни. Наши предки в древности какое-то время считали девятками (впрочем, похоже, что они все-таки считали восьмерками, а с девяти начинался уже новый отрезок счета). С тех пор прошло не менее семи - девяти столетий, но мы до сих пор трепещем перед грозным "девятым валом" или устраиваем поминки по усопшему на девятый день после кончины. Счет десятками возник около 3-2,5 тысячи лет до нашей эры в Древнем Египте. Претерпев небольшие изменения, древнеегипетская десятеричная система сначала обосновалась на Востоке (в Индии примерно к VI веку нашей эры, более известная как индийский счет), а затем через весьма активную торговлю в XI-XIII веках достигла пределов Древней Руси. От Орды Русь переняла десятичную систему счисления для весовых измерений и денежного счета, опередив в этом даже Европу, которая познакомилась с десятеричной системой счисления через арабов только в XIII веке, а усвоила ее и того позже. Однако окончательно эта система счисления прижилась в России вместе с реформами Петра I, пришедшими к нам из Европы. В Древней Руси (особенно в Новгородской республике XII-XV веков) был широко распространен счет, основанный на счислении числа фаланг на руке "счетовода". Счет начинался с верхней фаланги "перстка" (мизинца) левой руки, а заканчивался нижней фалангой ("низ перста") указательного пальца. Большой, или "палесъ великий", левой руки при этом последовательно осуществлял "подсчет" суставов на растопыренной пятерне. Досчитав до двенадцати, "счетовод" обращался к своей правой руке и загибал на ней один палец. Так продолжалось до тех пор, пока все пальцы правой руки не оказывались сжатыми в кулак (поскольку число фаланг на четырех пальцах было равно 12, получалось 12 пятерок, то есть 60). Кулак в данном случае символизировал пятерку дюжин, то есть "шестьдесят". Счет сороками (или "сороковицами") имел преимущественное распространение в Древней Руси. Число 40 (четыре десятка) долгое время называли "четыредцать" или "четыредесят". Но восемьсот лет тому назад для обозначения этого множества на святой и православной Руси впервые появилось название "сорок". До сих пор ученые спорят, откуда взялось это слово. Одни полагают, что его истоки находятся в греческом названии числа 40 - "тессаконта", другие утверждают, что оно появилось, когда Русь платила дань "сороковинами" (ежегодная ордынская подать, равная сороковой части наличного имущества). Третья группа исследователей убеждена, что это слово произошло от так называемых меховых денег и названия "сорочка ". Поэтому наши предки, например, на Русском Севере считали "сорока ми", а их собратья - сибирские звероловы вели счет "сорочками", то есть мешками для пушнины, в которых хранились звериные шкуры (преимущественно по 40 штук беличьих шкурок или по 40 собольих хвостов, шедших в XVI веке на пошив одной боярской шубы, именовавшейся "сорочкой"). О том, что число 40 на Руси когда-то играло особую роль при пальцевом счете, говорят и некоторые связанные с ним поверья. Так, сорок первый медведь считался роковым для российского охотника, убить паука - означало избавиться от сорока грехов и т.д. Все то количество, которое превышало некое множество (например, "сорок"), превосходящее всякое воображение ("сорок сороков") и не умещавшееся в голове российского землепашца из-за своей ничем не ограниченной величины, называлось одним словом - "тьма". на начало

Пальцевой счет, унаследованный от далеких предков, сохранился вплоть до настоящего времени и активно используется, например, судьей на боксерском ринге при отсчете секунд во время нокаута или на товарно-сырьевой бирже где-нибудь в Чикаго или Токио. Да и в быту он не забыт. И сегодня мы сгибаем (а американцы, наоборот, разгибают) пальцы, в споре показывая оппоненту ради большей убедительности количество аргументов в пользу своей позиции.

istrasvvt.narod.ru

Matematika_Teoria_Shpory

1. Характеристика понятий “число” и “счет” и их развитие в истории человечества Число́ — основное понятие математики, используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось. Письменными знаками (символами) для записи чисел служат цифры .Числа это неотъемлемое орудие современной цивилизации, используемое для упорядочения сферы ее деятельности. В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счёте возникла так же естественно, как и потребность в добывании огня. Любопытно отметить, что у многих народов для обозначения числа 1 применялся один и тот же символ вертикальная чёрточка. Это самое древнее число в истории человечества.. Число, важнейшее математическое понятие. Счёт — действие по значению глагола «считать»; вычисление, определение каких-либо количественных показателей или перечисление элементов последовательности чисел. На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Впоследствии способность различать друг от друга небольшие совокупности развивалась; возникли слова для обозначений понятий «четыре», «пять», «шесть», «семь. Для этого человек пользовался окружавшими его предметами, как инструментами счета: он делал зарубки на палках и на деревьях, завязывал узлы на веревках, складывал камешки в кучки и т.п. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков. На первых порах расширение запаса чисел происходило медленно. Сначала люди овладели счетом в пределах нескольких десятков и лишь позднее дошли до сотни. У многих народов число 40 долгое время было пределом счета и названием неопределенно большого количества На следующей ступени счет достигает нового предела: десяти десятков, и создается название для числа 100. Вместе с тем слово «сто» приобретает смысл неопределенно большого числа Число и счет являются продуктом человеческой культуры, своим появлением они в большой мере обязаны развитию торговли, земледельческим работам. История развития счета началась с умения устанавливать соответствие между количеством предметов (или частей предмета), нуждающихся в пересчете, и количеством пальцев на руке. Десять пальцев на руках явились самым первым и естественным орудием и средством счета. Позже в качестве орудия счета стали использоваться зарубки на дереве, камешки и т.д. Слово служило обозначением соотношения между группами предметов: объектов счета и орудий счета равно меньше больше.

2. Системы счисления и история развития письменных нумераций. Система счисления— это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. Непозиционной системой счисления называется такая система счисления, у которой количественный эквивалент («вес») цифры не зависит от ее местоположения в записи числа. Непозиционные, например Единичные, Алфавитные, Римская, Древнеегипетская. . Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления. В основе римской системы счисления лежат знаки I (один палец) для числа 1. Позиционные- количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. Первая позиционная система счисления была придумана еще В Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной В настоящее время наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьмеричная , шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание. Цифр, как и правил арифметики, никто сразу не выдумал, не изобрел. Мысли и слова выражались, при помощи рисунков на скалах, на стенах пещер, на камнях. Для запоминания чисел люди пользовались зарубками на деревьях и на палках. Далее естественно стали обозначать число один одной черточкой, два — двумя, три — тремя черточками и т. д. В Древнем Египте около 4000 лет назад имелись другие значки и иероглифы для обозначения чисел. дальнейшем появляются особые обозначения отдельных звуков, то есть буквы. Было время, когда буквами пользовались и в качестве цифр. Так поступали древние греки, славяне и другие народы. Чтобы отличить буквы от чисел, славяне ставили над буквами, изображающими числа, особый знак "—" , названный «титло». Арабы заимствовали у индийцев цифры и позиционную десятичную систему, которую европейцы в свою очередь заимствовали у арабов. Поэтому наши цифры, в отличие от римских, стали называть арабскими. Правильнее было бы их называть индийскими. Эти цифры употребляются в нашей стране начиная с XVII в. Римские же цифры применяются лишь в исключительных случаях.

3. Геометрические фигуры и становление представлений об эталонах формы предметов в истории человечества. Возникновение геометрических понятий или понятий о геометрических фигурах произошло в глубокой древности при изготовлении скребков в форме дисков, круглых сосудов, конусойдных зданий и пр. Большинство общепринятых в настоящее время в геометрии названий геометрических фигур является греческими, обозначающими различные предметы той или иной формы, с которыми люди сталкивались в своей практической деятельности. в геометрии сначала появились геометрические эталоны: мяч - для шарообразных предметов, сосновая шишка - для остроконечных и т.д., а впоследствии названия этих эталонов стали названиями абстрактных геометрических фигур. В более позднее время в геометрических орнаментах появились и числовые отношения, Так, На развитие геометрического мышления существенно повлияло и развитие зарождающейся астрономии. Уже первобытные племена кочевников-скотоводов наблюдали за движением звезд и пользовались звездами как ориентирами. Становление обмена и мореплавания привили к дальнейшему развитию астрономических знаний. “Но астрономические знания немыслимы без развития знаний математических. Вначале случайное, а впоследствии все более и более систематические наблюдения небесного свода привело к ознакомлению со свойствами шара, круга и угловых направлений Исходным содержанием понятия о форме являются реальные предметы окружающей действительности. Форма — это основное зрительно и осязательно воспринимаемое свойство предмета, которое помогает отличать один предмет от другого. Человечеством создана система эталонов для обозначения форм конкретных предметов. Это система геометрических фигур. Группировка геометрических фигур может быть представлена следующим образом: плоские и объемные, имеющие углы и не имеющие их, т. е. округлые, различающиеся по внешним признакам. Таким образом, геометрические фигуры выступают образцами, эталонами формы реальных предметов или их частей.

4 характеристика понятия «величина» и история развития способов и единиц измерения протяженностей массы и объема веществ Величина-одно из основных математических понятий,возникшее в древности и подвергшееся в процессе длительного развития ряду обобщений. Общее понятие величины-непосредственное обобщение более конкретных понятий:длины,площади,объма,массы,скорости и т.д.каждый конкретный род величин связан с определенным способом сравнения соответствующих свойств с определенным способом сравнения соответствующих свойств объектов. потребность в измерении всякого рода величин так же как потребность в счете предметов возникла в практической деятельности человека на заре человеч.цивилизации.. Эти сравнения еще не были измерениями.далее процедура сравнения была усовершенствована.одна какая нибудь величина принималась за эталон,а другие величины того же рода (длины. площади, объема, массы )сравнивались с эталоном. Когда люди овладели знаниями о числах и их свойствах величине-эталону приписывалось число 1 и этот эталон стал называться единицей измерения. Цель измерения стала-оценить сколько единиц содержиться в измеряемой величине.результат измерения стал выражаться числом. При сооружении жилищ людям приходилось выполнять разные измерения. требовалось измерять длины при строительстве жилищ, при изготовлении различных орудий труда, на охоте, рыбной ловле… Вначале для измерения длины (так же как и при счете) люди пользовались руками, пальцами. Например, чтобы измерить длину стрелы, ее сравнивали с длиной руки от локтевого сустава до конца среднего пальца, в результате появилась единица длины – локоть. . Расстояние, на котором надо было вбить в землю колья при постройке хижины, человек измерял шагами или длиной ступни своей ноги. Отсюда произошла единица длины, которая в одних местностях называли лапоть, в других фут (в переводе с английского означает «нога»). У древних египтян за много веков до начала нашего летоисчисления за единицу длины был принят локоть. У них было установлено соотношения локтя и других единиц: 1 локоть равен 6 ладоням, 1 ладонь содержит 4 пальца, в 1 локте 24 пальца, Это уже целая система единиц длины.Более крупная единица длины была установлена в Вавилоне следующим образом. Человек с появлением солнечного луча, отметив начало пути, шел по прямой линии. Когда весь солнечный диск выходил из-за горизонта, человек останавливался и отмечал конец пути. Такая единица длины впоследствии была принята и в Древней Греции. Ее назвали стадия. Отсюда и название стадион. Подобно тому, как в Вавилоне была установлена стадия, в Древнем Риме была определена единица измерения площадей – югер. Этой единицей служила площадь, которую можно было вспахать на паре волов за один день работы. У арабов за мельчайшую единицу длины был принят поперечник круглого макового зернышка. 7 таких единиц составляли длину поперечника горчичного зерна. 7 горчичных зерен равнялись длине ячменного зерна. 7 зерен ячменя по длине укладывались на отрезки, равном суставу большого пальца. Предполагают, что длина сустава большого пальца послужила прообразом единицы, впоследствии названной дюймом. В 1101 г. Король Англии Генрих 1 приказал измерить расстояние от кончика его носа до кончика среднего пальца вытянутой руки. По этой мерке был изготовлен образец ярда, который стал официальной единицей длины в Англии. В одном из сочинений 16 в. сказано: «Нужно, чтобы 16 человек высоких и низких, когда они, например, выходят из церкви, поставили свои ботинки один перед другим; эта длина должна быть законной мерой, которой надлежит мерить поля». Шестнадцатая доля этой меры была названа футом. Древними русскими мерами в 16в. были пядь (ладонь), локоть (позже аршин), сажень, верста, или поприще. пользовались мерой лапоть. В России пользовались двумя видами саженей – маховой и косой. Маховая сажень – это расстояние между концами пальцев, раздвинутых на полный мах рук. Косая сажень – расстояние от концов пальцев поднятой вверх правой руки до конца пальцев левой ноги. На Руси также употреблялась мера для измерения объемов, но применялись и другие единицы: бочка, или кадь (40 ведер), ведро. Десятую долю ведра составлял штоф, а сотую часть ведра называли чаркой. С ведением метрической системы мер за единицу жидкости и сыпучих тел принят литр и декалитр. О более древних единицах объема сведения до нас не дошли. Древние вавилоняне для определения массы создали свою систему единиц. У них за мельчайшую единицу массы принимался шекель, или сикля. Более крупные единицы – шестьдесят шекелей – составляли мину (ману). Шестьдесят мин составляли билту, а у некоторых народов ее называли талант. Первые образцы единицы массы (фунт) и единицы длины (аршин) были изготовлены на Руси в 1747 г. при этом было установлено, что 40 фунтов составляют пуд, а десять пудов составляют берковец. Однако последняя единица употреблялась редко. До установления этих мер у славян единицей массы была гривна, представляющая собой слиток серебра весом около 400 г. ). Серебряная гривна одновременно служила и денежной единицей, подобно вавилонскому шекелю.

5 характеристика понятия «время» и история развития представлений человечества об измерении времени. Все календари можно разделить на следующие типы: солнечные, лунные и лунно-солнечные. Все эти календари используют естественные периодические процессы - сутки, то есть смену дня и ночи, смену фаз Луны, которые происходят на протяжении месяца, или смену времен года между двумя весенними равноденствиями, то есть период так называемого тропического года. На ранних этапах развития человечества представление о В. носило циклический характер (циклическое В.), что было вызвано исключительной важностью для человеческого существования циклических процессов: годичного и суточного циклов, цикла обращения Луны и, возможно, внутренних биоритмов организма и смены поколений. Реликтом такого циклического понимания В. является восточный календарь. В привычном нам календаре продолжительность года примерно равна времени, которое затрачивает наша планета, чтобы совершить оборот вокруг Солнца. Продолжительность месяцев связана с движением Луны, а дни - это обороты Земли вокруг собственной оси. Но бывали календари, время в которых делится по куда более странной логике. В основе календаря индейцев майя лежал период продолжительностью в 260 дней. О происхождении такого календаря историки до сих пор спорят. Согласно одной из теорий, всё дело в цифрах: числа 13 и 20 имели особое значение для майя. Другие учёные полагают, что такой календарь изобрели повитухи, чтобы предсказывать, скоро ли закончится беременность. Справедливости ради, стоит заметить, что майя использовали и другие методы учёта времени, в том числе и похожие на распространённый сейчас 365-дневный календарь. Вдобавок, у индейцев был и так называемый "долгий счёт", с помощью которого они измеряли протяжённые отрезки времени в смешанной 20, 18 и 13-ричной системе. Общий цикл данного счёта заканчивается 21 декабря 2012 года. Некоторые почему-то считают, что вместе с концом счёта должен прийти и конец света. Тысячелетние" часы. Первый прототип "тысячелетних" часов построил в 1986 году Дэнни Хилис. Сейчас это устройство находится в лондонском Музее науки, и оно уже однажды прозвонило. Это произошло, когда годовая стрелка часов сдвинулась с деления 1999 на деление 2000. Следующего раза придётся ждать 993 года. При создании таких часов приходится учитывать множество факторов. Отсутствие частей из дорогостоящих металлов очень важно, иначе велик шанс, что когда-нибудь устройство сломают мародёры. Простота в эксплуатации необходима, чтобы обслуживание часов не превратилось в проблему для будущих поколений. Естественно, рабочие части механизма должны быть на виду, иначе для изучения, починки и усовершенствования его придётся разбирать. И самое главное: часы должны показывать точное время все десять тысяч лет. Десятичное время. Хотя для счёта люди давно используют десятичную систему счисления, следы древней двенадцатеричной системы сохраняются в единицах измерения времени. Все мы знаем, что в сутках у нас 24 часа (то есть, 2*12), в каждом часе 60 минут (5*12), а в каждой минуте - 60 секунд. Несколько раз в истории человечества применялось десятичное время. Согласно этой системе измерения времени, в сутках 10 часов, разделённых на 100 минут, состоящих из 100 секунд. Её активно использовали в древнем Китае. День у древних китайцев состоял из ста частей под названием "кэ", а месяц - из 10 дней, называемых "сюнь". Десятичное счисление времени было введено и во Франции после французской революции. Бедных французов заставляли переходить на него с 1795. Через десять лет от десятичного времени отказались. Была, правда, попытка восстановить десятичный счёт времени в 1897 году, но она провалилась.

6 Сущность монографического метода обучения арифметике и его влияние на методику развития математических представлений у дошкольников. Становление методики формирования элементарных математических представлений в XIX—начале XX в. происходило под непосредственным воздействием основных идей школьных методов обучения арифметике. В то время единой методики преподавания арифметики не существовало. Шла длительная борьба между двумя направлениями, с одним из которых связан так называемый метод изучения чисел, или монографический, а с другим — метод изучения действий, который называли вычислительным

Монографический метод - это метод, по которому изучали числа с помощью графических изображений, т.е. метод целостного восприятия чисел. Монографический метод получил определение метода, описывающего число. Д.Л. Волковский «Детский мир в числах», включил систему освоения чисел на основе монографического метода. Согласно методу изучения чисел в разработке немецкого методиста А. В. Грубе преподавание арифметики должно идти (в пределах. 100) от числа к числу. Каждое из этих чисел, якобы доступное «непосредственному созерцанию», сравнивается с каждым из предыдущих чисел путем установления между ними разностного и кратного отношения. Действия должны как бы сами вытекать из знания наизусть состава чисел. В процессе изучения каждого числа материалом для счета служили пальцы на руках, штрихи на доске или в тетради, палочки. Например, при изучении числа 6 предлагалось разложить палочки по одной. 1.Задавались вопросы: «Из скольких палочек составилось наше число? Отсчитайте по одной палочке, чтобы получилось шесть. Во сколько раз шесть больше одного? Какую часть шести составляет одна палочка? Сколько раз одна палочка заключается в шести?» И т. д. 2.Потом изучаемое число точно так же сравнивалось с числом 2, предлагалось разложить шесть палочек по две и отвечать на вопросы: «Сколько двоек в шести? Сколько раз два содержится в шести?» И т. д. Так данное число сравнивалось со всеми предшествующими (3, 4, 5). После каждой группы таких упражнений действия записывались в виде таблицы, результаты которой заучивались наизусть, с тем чтобы в дальнейшем по памяти производить все арифметические действия, не прибегая к вычислениям. В 90-х годах под влиянием критики монографический метод обучения арифметике был несколько видоизменен немецким дидактом и психологом В. А. Лаем. Книга В. А. Лая «Руководство к первоначальному обучению арифметике, основанное на результатах дидактических опытов» была переведена на русский язык. обучение по Лаю Детям показывали числовую фигуру. Они ее рассматривали, а затем описывали с закрытыми глазами расположение точек. Например, фигура, обозначающая число 4: один кружок — в левом верхнем углу, один кружок — в левом нижнем углу, один кружок — в правом верхнем углу и один кружок — в правом нижнем углу. В. А. Лай считал, что, чем отчетливее, яснее и живее наблюдение вещей, тем отчетливее, яснее и живее возникают числовые представления. За описанием следует зарисовка данной числовой фигуры и составление ее на счетах. После работы над образом числа дети переходили к изучению его состава. Педагог закрывал три кружка из четырех (дети воспринимали один верхний левый), затем он закрывал и этот кружок, а первые три открывал или закрывал два кружка. Результаты каждого действия описывались и объяснялись: один да три будет четыре; три и один будет четыре; два и два будет четыре. После этого на изученный состав числа 4 решались задачи. Ответ давался без вычислений, на основе запоминания состава числа. По этому методу дети воспринимали и запоминали числа, предлагаемые им в виде квадратных числовых фигур. Последовательность обучения по монографическому методу состояла в следующем: а) описание, наблюдение и составление некоторой числовой фигуры; б) изучение состава числа и запоминание числа; в) упражнение в арифметических действиях Однако уже в 70-х годах XIX в. стали появляться противники монографического метода. В 1874 г. в журнале «Отечественные записки» (№ 9) критике его подверг Л. Н. Толстой. «В этих немецких приемах,— писал он в статье «О народном образовании»,— была еще и та большая выгода для учителей... что при них учителю не нужно... работать над собою и правилами обучения. Большую часть времени по этой методе учитель учит тому, что дети знают, да, кроме того, учит по руководству, и ему легко». недостатки монографического метода: Во-первых, критиковалось исходное положение метода, согласно которому число в пределах 100 можно якобы наглядно представить себе как группу единиц. Такой способности не существует, говорили критики. Мы наглядно можем представить себе группу из двух — четырех предметов. А при большем количестве всегда приходится прибегать к счету. Поэтому изучать числа и их состав путем разложения числа бессмысленно. В пределах 100 таких разложений свыше 5000, запомнить которые невозможно. Во-вторых, монографический метод критиковали за томительную скуку и крайнее однообразие приемов обучения, при котором дети не осмысливали значения каждого арифметического действия, не дифференцировали их: обучение сводилось лишь к тренировке памяти и определенных навыков. Механическое заучивание начал арифметики при однообразии методических приемов отбивало желание у учащихся заниматься дальше. Несмотря на критику монографического метода, непризнание его в русских школах, поклонник этого метода Д. Л. Волковский издал книгу «Детский мир в числах» (1912). Книга иллюстрировалась числовыми фигурами В. А. Лая, карточками и чертежами. Она была предназначена не только для начальной школы, но и для приготовительных классов женских гимназий, детских садов и домашнего обучения. Монографический метод проник в детский сад, и по нему сравнительно долго (вплоть до настоящего времени) строилось обучение детей счету

7. Сущность вычислительного метода обучения арифметике. Вычислительный метод возник как противоположность монографическому. Вычислительный метод по-другому называется «метод изучения действий», Его сущность основана на идее освоения со считывания (аналитического восприятия множества), обучении сущности арифметических действий на наглядных материалах. Детей обучали считать конкретные множества, усваивать нумерацию, а затем переводили к изучению арифметических действий и вычислительных приёмов. Т. е. обучение шло от практических действий с множествами к усвоению операции счёта и пониманию числа, а затем - усвоению понятия натурального ряда чисел и пониманию построения десятичной системы счисления. Обучение и пояснениевелось по десятичным концентрам(сначала в пределах первого десятка, затем по аналогии – в пределах 20 и т.д.). Этот метод предполагает научить детей не только вычислять, но и понимать смысл этих действий, основу десятичного исчисления. Обучение при этом строится по десятичным концентрам. В пределах каждого концентра изучаются не отдельные числа, а счет и действия. Разновидностью данного метода стали представления о необходимости обучения действиям на материале задач. Этот метод предложили в конце 19 в.: П.С. Гурьев в России, А. Дистервег в Германии («Руководство к преподаванию арифметики малолетним детям»). Их последователи в России: А.И. Гольденберг, С.И. Шохор-Троцкий, Ф.И. Егоров.

8. Вклад Е.И. Тихеевой в становление методики формирования математических представлений у детей дошкольного возраста Е.И. Тихеева считала, что формир числовых представлений должно осущ-ся у ребенка естественно, в ходе его развития, без принуждения и давления. Отсюда – требования к объему знаний, материалу, методам, разработанным ею. Это требования сводятся к необходимости создания условий для легкого и непринужденного усвоения знаний. Такое усвоение возможно обеспечить не в условиях коллективного обуч, а в игре и повседневной детской жизни. В своих книгах «Современный д/с», «Счёт в жизни маленьких детей» (1920) Тихеева высказывается против систематического обучения дошкольников. Считает, что до 7 лет дети должны сами научиться считать в процессе игры и повседневной жизни. Но возражает против полной стихийности обуч. Рекомендовала спец игры-занятия с разработанным ею дид матер (парные карточки, лото). Счетный материал – естественный матер (камушки, шишки, пуговицы и т.д.).Определила объем знаний дошкольников: усвоение первого десятка, действия сложения и вычитания с их записью, ознак с предметами разной величины, представления об объёме и массе.

9. Роль Ф. Н. Блехер в развитии методики формирования математических представлений у дошкольников Ф.Н. Блехер, книга «Математика в д/с и нулевой группе» (1934) стала первым учебным пособием и программой по математике для советского д/с. В прогр-ме использовались данные зарубежных психологов о времени и сроках восприятия реб разных чисел и предлагалось научить детей 3-4-летнего воз различать и выделять понятия «много» и «один», формир у них представ о числах 1,2,3 на основе соответствующих совокупностей. Ср дош воз: определять количественные хар-ки предметов в пределах 10, на основе счета сравнивать числа, производить действия + и - . Ст.гр: знать состав чисел, освоить второй десяток, научить решать простые арифметич задачи. Считала счёт средством всестороннего развития. Разработала игровые методы.

 10 Вклад А. М. Леушиной в т и м развития элементарных математических представлений у детей дошкольногоЛ защитила докторскую диссертацию «Подготовка детей к усвоению арифметики в школе. Знания о колл-х отношениях формируются у детей в процессе деятельности с предметами. Л Ввела программу матем-го образования дошк-в, создала дидакт-й материал, необходимый для освоения программы; показала роль игр, игровых упражнений и разных видов деятельности для закрепления знаний. Все необходимые представления о множестве, представления количественные, временные, понятия числа, должны даваться детям в определенной последовательности. Дети овладевали счетом попутно, главной задачей было изучение состава чисел в пределах десятка.(путь заимствован из монографического м-да в школе )Целесообразно одновременно приучать детей раскладывать предметы правой рукой слева направо, что готовит руку и глаза ребенка следовать ряду слева направо в соответствии с направлением букв в строке. Занятия по счету проводятся один раз в неделю, без перерывов. Последовательность, постепенность и систематичность в обучении детей дош. возраста счету обеспечат преемственность в работе между ДОУ  и школой. Этапы: 1​На ранних этапах формируется представление о множестве как целостном единстве, состоящем из отдельных элементов. 2​На основе представлений о множестве можно обучать детей счету с помощью слов-числительных, у 4-леток. 3​необходимо обеспечить восприятие множеств на слух, по осязанию и воспроизведение множеств в движении, а также развить умение считать элементы этих множеств.4​Важно подвести детей к пониманию отношений между смежными числами в пределе пяти в прямом и обратном порядке, опираясь на сравнение различных множеств.5​В старш. группе углубить понимание отношений между смежными ч. в пределе десяти, познакомить с количественным и порядковым значением числа, из этого формир-ся представления о натуральном ряде как системе чисел; показать приемы разложения числа на 2 меньших числа, в целях подготовки детей к арифм-м действиям. Материалом для счета могут служить различные мелкие игрушки, знакомые детям по тематике: тарелки, чашки, рыбки, и т. д. Важно многообразие его. Наглядный материал (раздаточный или демонстрационный) должен быть динамичным, чтобы с ним можно было действовать в соответствии с заданиями воспитателя. Для усвоения представлений о множестве важно обеспечить также восприятие множества на слух.  Звуки могут быть разнообразными, они различаются по своему характеру: падение капель воды, бой часов, стук двери и др. дети считают количество звуков, они учатся воспринимать различные множества на слух.

studfiles.net

Смотрите также

• 
  Презентация древние деньги
• 
  Древние деньги презентация
• 
  Театр японии древней
• 
  Театр древней японии
• 
  Питание древних греков
• 
  Иероглифы картинки древние
• 
  Древние китайские династии
• Древнее проснулось зло
• 
  Демиурги древняя греция
• 
  Викторина египет древний
• 
  Музей древних артефактов