Цифры разных стран и племен. Смайлики, жабы и узелочки. Древние цифры
История возникновения цифр - древние числа и цифры Руси, Рима, Китая, Египта, Вавилона и ГрецииВсматриваясь в причудливые знаки, не сразу поймешь, что символизируют древние числа и цифры. Мешки с крупами, орудия труда. В хвостатых, изогнутых знаках читается менталитет древнего народа, уровень его развития, навыки, экономическая обстановка. Обозначения цифр сотканы из глубоких абстракций и художественных представлений о мире. Рождение цифр неразрывно связано с возникновением письменности, но узелковое письмо шумерских народов появилось даже раньше. Оно было создано для счета. О чем это говорит? Уметь считать было важно во II в. до н.э., и в высокотехнологичном ХХI столетии. 
Числа и бизнес пребывают в прочном тандеме. Числа нужны для основания и раскрутки бизнеса (для вычисления рентабельности, расчета конверсии, КПД), а бизнес нужен для хороших цифр на счету в банке. Счет стал неотъемлемой частью человеческого мышления и настолько влился в повседневную жизнь, что мы даже не замечаем его. Предприниматель должен числа не просто видеть, считать и предполагать, а читать. Созерцать не глазами, а разумом. Вернуться к оглавлению Как мир учился считатьЦифры и числа – это разные понятия. В обиходе мы их путаем, но существенная разница в сути слов от этого не исчезла. Цифра служит для условного обозначения числа. Число выражает количественную характеристику в цифрах, и представляет собой более обобщенное понятие. Если проанализировать, какими были первые цифры, можно увидеть обширную историю культуры отдельного народа. Составление обозначений для чисел потребовало более высокого интеллектуального уровня. Поэтому наши предки оставляли тысячи зарубок на твердых материалах. Столько, сколько требовалось. Так, наивно, но достоверно, заполнялись древние отчетные документы, «чеки» и т.п. Первые цифры представляли собой примитивные засечки и значки.  Пример древних чисел и цифр Генезис цифр останется для ученых неизведанной Марианской впадиной. Витиеватая история возникновения вызывает замешательство. Точно известно, что первые попытки письменной фиксации цифр были в Египте и Месопотамии: найденные древние математические записи тому свидетельство. Эти государства располагались далеко друг от друга, письменность и культура в каждом из них уникальна. В Древнем Египте сформировалось скорописное иероглифическое письмо, месопотамские писцы использовали клинопись. Поэтому египетские первые цифры своей формой передавали природу всех окружающих предметов: животные, растения, предметы быта и т.д. Папирус Ринда (1650 г. до н.э.) и папирус Голенищева (1850 г. до н.э.) – числовые древнеегипетские документы — свидетельствуют о высоком культурном развитии народа. Месопотамская клинопись запечатлена на глиняных табличках, на которых цифры представлены небольшими клиньями, повернутыми в разные стороны соответственно своему значению. И в египетских, и в месопотамских системах счисления есть цифры от 1 до 10, особые метки для обозначения десятков, сотен и тысяч, и ноль, который обозначали выделенным пустым местом. Числа древнего Египта построены грамотно и логично. Рационализм и четкость отличают эти системы счисления от аналогичных попыток других народов. Цифры значением меньше десяти обозначались ׀. Например, цифра 6 выглядела как ׀׀׀׀׀׀. Число 10 обозначалось перевернутой подковой в иероглифической системе и особым символом – в иератической. Сколько десятков в числе, столько и «подков». Иератическая система письменности предполагала для каждого числа, на десяток выше предыдущего, отдельный символ. Начиная от 100, это была стилизованная клюшка, над которой с каждой новой сотней ставили крохотную пометку.В иероглифах все проще. Число 100 выглядело почти как арабская цифра 9, но египтяне назвали ее лотосом. Далее все аналогично — 200 – 2 «лотоса», 300 – 3 и т.д.  Египетские числа и цифры Вы заметили, что в древнем Египте с самого начала сформировалась десятичная система? Однако Месопотамия все же превзошла Египет, когда на ее территории обрел независимость и возвысился Вавилон. Там вырастала отдельная культура, вскормленная достижениями соседних завоеванных государств. Вернуться к оглавлениюДостижение ВавилонаЧисла древнего Вавилона мало отличались от месопотамских: те же клиновидные знаки служили для обозначения единиц - ˅, и десятков - ˃. Комбинация этих знаков применялась для обозначения чисел 11-59. Число 60 в письме выглядело как зеркальное отражение буквы «Г». 70 – Г˃, 80 - Г˃˃ и так далее, принцип ясен, клинопись не отличается гениальностью.  Вавилонская система счисления Основная ценность заключается в том, что один и тот же знак – обратите внимание – в зависимости от того, где он расположен в записи числа, имеет разное значение. Речь идет о поместном размещении знаков в системе счисления. Те же клиновидные знаки, указанные в разных разрядах, обладают разной значимостью. Поэтому Вавилонскую систему счисления с нулем принято называть позиционной. Математики могут с этим поспорить, потому что не найдено ни одного источника, в которой ноль располагался бы в конце числовой записи, что говорит об относительной позиционности. Вавилонская система стала своеобразным трамплином, с которого человечество совершило прыжок на новый этап своего развития. Идея со временем попала в руки индусов. Они внесли свои коррективы, усовершенствовав систему счисления. Переняли идею итальянские торговцы, которые привезли ее в Европу вместе с товаром. Позиционная система счисления облетела весь мир, обогатив своим появлением не только математические науки, но и современный счет. 
Знаете, откуда взялось деление часа на 60 минут, а минут – на 60 секунд? Из рассмотренной выше шестидесятеричной системы чисел. Взгляните, как обозначали числа древние вавилоняне, и в клиновидных значках увидите сакральный смысл современного, привычного для всех счисления. Вернуться к оглавлениюИстория цифр разных народов Вернуться к оглавлениюЦифры древней ГрецииПод плеядой легендарных античных математиков и философов сформировалось две системы счисления. Каждая из них приносила свои преимущества, но они не были открыты или доработаны в связи с политико-культурными переменами. Аттическую систему можно было бы назвать десятичной, если бы в ней не была выделена цифра 5. Аттическая запись чисел использовала повторы коллективных символов, что напоминало месопотамский метод. Единицу обозначала черта, написанная нужное количество раз. Таким образом записывались числа до 4. Цифра 5 была под первой буквой слова «пента», 10 – под первой буквой слова «дека» («десять») и т.д. История чисел и цифр: Алфавитная (или ионическая) система достигла своего расцвета в преддверии Александрийской эпохи. По сути, объединила десятеричную систему счисления и древневавилонский способ позиционности. Цифры записывались буквами и черточками. Система счисления довольно перспективна, но греки с их фанатичным стремлением к совершенству так и не довели ее до ума. Пытаясь достигнуть максимальной строгости и четкости в числовых записях, математики внесли существенные трудности в работу с ней. Вернуться к оглавлениюЧисла древнего РимаЛегкоузнаваемые, четкие, строгие и ясные обозначения стали весьма удачным изобретением римлян. Пройдя сквозь века, символы остались практически неизменными еще и потому, что Рим пользовался влиянием на древней государственной арене. А также перенимал некоторые культурные особенности у завоеванных народов. Бросается в глаза алфавитное обозначение цифр – главная «изюминка» аттической системы. Цифра V (5) – прототип ладони с раскрытыми пятью пальцами. Стало быть, Х (10) – две ладони. Палочками указывали единицы, а для сотен и тысяч предназначены прописные буквы алфавита.  Числа и цифры древнего Рима Вернуться к оглавлениюЦифры древнего КитаяСистема сложных, абстрактных иероглифов, в которую превратились невинные зарубки на гадальных костях, мало где применяется. Впрочем, иероглифы используются для формальных записей, а упрощенный набор символов применяется в повседневной жизни. 
Вернуться к оглавлениюЧисла в древней РусиКак ни странно, Русь повторила алфавитную систему счисления. Каждая цифра была названа соответствующей ее рангу буквой алфавита. Цифра 1 выглядела как «А», 2 – «Б», 3 – «В» и т.д. Десятки и сотни также были подписаны соответствующими буквами славянского алфавита. Чтобы не путать в тексте слова с цифрами, над числовыми записями рисовали титло – горизонтальную волнистую линию.  числа и цифры Древней Руси Вернуться к оглавлениюДревнеиндийские цифрыСколько бы ни спорили ученые, сколько бы изменений ни претерпевала форма цифр, но возникновение арабских, «наших» цифр приписывают древней Индии. Возможно, арабы позаимствовали древнеиндийскую систему счисления или изобрели ее сами. Причиной научных мытарств стал фундаментальный математический труд Аль-Хорезми «Об индийском счете». Книга стала своеобразной «рекламой» десятичной позиционной системы. Иначе как объяснить внедрение индийской системы счисления на территории всего Халифата?  Эволюция индийских чисел и цифр Полноценность позиционной системы укрепилась возникновением «нуля». В целом запись чисел не ушла далеко от аттической: для цифр 5, 10, 20… использовались коллективные символы, повторяющиеся нужное количество раз. При таком подходе из древнеиндийских цифр не могли «вырасти» арабские. Это утверждение кажется логичным на первый взгляд, но история цифр загадочна, и демонстрирует непричастность древней Индии к возникновению знакомых нам символов. Вернуться к оглавлениюСамые распространенные системы счисленияАрабские цифры значительно экономили время и материалы для письма. Один арабский ученый предложил обозначать цифру символом с определенным количеством углов. Количество углов должно равняться значению цифры. Например, «0» - «ничто», углов нет; 1 – 1 угол; 2 – 2 угла и т.д. Слово «цифра» также позаимствовано из арабских языков, где оно звучало как «сыфр», и обозначало «ничто», «пустота». У «сыфр» был синоним – «шунья». На протяжении веков «0» называли именно так. До тех пор, пока не появилось латинское «нуллум» («ничто»), как мы и называем «ноль». 
Современный вариант символьного обозначения цифр выражен плавными, округлыми линиями. Это результат эволюции. В первозданном виде обозначения угловаты. Время действительно способно сглаживать углы – в прямом и переносном значениях. Неважно, откуда берет истоки история возникновения чисел, главное, они стали достоянием всего мира. Цифры легко пишутся и запоминаются, что облегчает и смысловое восприятие. Ведь перед вами не длинная вереница закорючек и букв. Несмотря на то, что латынь называют «мертвым» языком, ее значимость в научной сфере подтверждена изучением в ВУЗах. Латинские цифры также нашли применение в документоведении, деловодстве, оформлении научных работ. Доступность, понятность и четкость сделали их завсегдатаями учебников и рефератов. Как сделать латинскую запись числа? У вас есть 7 знаков, комбинируя которые вы составите необходимое обозначение. Эти знаки легко запомнить: I – 1, V – 5, Х – 10, L – 50, D – 500, M – 1000. - Если знак, обозначающий меньшее число, расположен за большим числом, меньшее прибавляется к большему. Например, ХI – 11.
- Если символ меньшего числа стоит впереди, т.е. слева, нужно вычесть его от большего числа. Например, ХIХ – 19, а не 21.
Проанализировав указанные факты и взаимосвязь между ними, вы поймете, что история чисел и системы счисления не могут рассматриваться раздельно. Системы счисления формировались одновременно с числами. Культурная, экономическая, политическая ситуация каждого государства подготовила почву для их формирования, что объясняет различия между системами счисления. Вернуться к оглавлению«Биография» арабской цифры Вернуться к оглавлениюИстория цифры 1.Не только первая цифра в ряду, но и символ единства, совершенной целостности, как бог или космос. Смысл числительного «первый» семантически связано с именем Адама («первый человек»), а также с именами мифических персонажей Атум (созвучно со словом «атом», а мы знаем, что он неделимый), Один (от сканд. «первый», «верховный», «главенствующий»). Чувствуется фонетическое подобие слова «один» с «ЕДИНый», «жАДИНа». Улавливаете сходство? 
Вернуться к оглавлениюИстория цифры 2В названии цифры чувствуется парность, бинарное противопоставление, антонимичность, дуальность, четность. 2 – это защита от небытия и одиночества, противостояние единому. Вспомним, что Адам значит «первый», но после него не землю пришла Ева, она была «вторая». Ева значит «дева», а поскольку в древней Руси буквы «о» и «е» отсутствовали, то слово «дева» в письменном варианте выглядело как «дъва». Учитывая глубокую религиозную приверженность наших предков, имя «два» могло произойти из христианской мифологии. 
Вернуться к оглавлениюИстория цифры 3Недаром китайский цифровой ряд начинается с «тройки». Это совершенное число, за которым стоит ряд русских традиций – трижды постучать по дереву, трижды произнести «аминь» по окончанию молитвы, бог в православной вере существует в трех ипостасях. Цифра 3 обозначает крайнюю степень какой-либо характеристики. Например, «треклятый», «трисвятый». «Тройка» пишется практически одинаково с буквой «з», с которой начинается слово «земля». Как одна из стихий (1 – огонь, 2 – вода), земля вполне может оказаться третьей. 
Вернуться к оглавлениюИстория цифры 4Сравните русское слово «веер» с немецким словом «vier» («четыре»). Четвертая стихия – ветер - прячется под «четверкой». Кроме того, это четное число, «четыр». Оттуда и название. 
Вернуться к оглавлениюИстория цифры 5Одна из важнейших характеристик микро- и макрокосма. Ничего загадочного в этом нет. Вспомните, сколько у нас чувств, сколько классов животных, сколько элементов в буддийских упанишадах? Их пять. Цифра 5 находится у истоков навыков счета. В древней Руси считали «на пятках», то есть на пальцах руки. Выражение «знать, как пять своих пальцев», родом из той эпохи. 
Вернуться к оглавлениюИстория цифры 6На Руси цифру записывали под буквой «зело», пока не были введены арабские цифры. Сравните слова «зело» и «зло». Ведь 666 – три «зело» - обозначает абсолютное зло, треклятое (см. историю цифры 3). 
Вернуться к оглавлениюИстория цифры 7Цифра 7 начертанием и произношением сходна с латинской буквой Z («zet»). «Семь» созвучно с «земь», то есть «опора», «центр». 
Вернуться к оглавлениюИстория цифры 8Сразу слышится «осемь», т.е. «ось». Цифра 8 напоминает букву «В», с которой начинается ее буквенная запись. 
Вернуться к оглавлениюИстория цифры 9Мы слышим троекратное повторение триады. «Девятка» - это обобщение всего цифрового ряда и ее превосходство одновременно. 
Зная историю возникновения чисел, вы будете смотреть на них через призму своих знаний, будучи осведомленным о том смысле, который они таят под своим начертанием. Может, вы интуитивно догадывались об этих смыслах? dengivsetakipahnyt.com История чисел | Любопытные подробности обо всем на свете! 
История чисел История возникновения чисел очень глубокая и давняя. Сама жизнь привела людей к тому, что стало просто необходимо использовать символы для написания чисел. 
История чисел Представьте, ведь давным-давно во времена, когда у людей не было цифр и они не умели считать как мы сейчас, у них все-равно возникало огромное количество поводов для счета. Правда, в те времена им не нужно было применять огромные числа. И самый простой вариант счета подсказала природа. Люди использовали пальцы рук, а при больших числах и ног, чтобы посчитать, например, количество голов скота в стаде. Если уж своих пальцев не хватало, звали приятеля, чтобы уже считать на его руках и ногах. Достаточно неудобно было, а вдруг никого рядом не окажется когда срочно нужно посчитать большое количество чего-нибудь? Потом кто-то придумал делать глиняные кружочки для подсчета. Например, повел пастух с утра большое стадо на пастбище. Подсчитал всех животных с помощью кружков — сколько кружков, столько животных. Вечером привел их домой, опять смотрит, чтобы каждому животному соответствовал один кружок. Ну и подобных вариантов существовало множество, то есть пользовались подручными средствами. Первое доказательство использования древними людьми счета — это волчья кость, на которой 30 тысяч лет назад сделали зарубки. Притом они набиты не как-нибудь, а сгруппированы по пять. Древность. В Древности у разных народов существовали свои способы счета. Например, майа использовали только три обозначения: точку, линию и эллипс и записывали ими любые цифры. В Древнем Египте около 5000-4000 лет до н.э. использовали такую запись чисел: единица обозначалась палочкой, сотня — пальмовым листом, а сто тысяч — лягушкой (в дельте Нила было очень много лягушек, вот у людей и возникла такая ассоциация: сто тысяч — очень много, как лягушек в Ниле). А вот наши предки-славяне использовали самую сложную запись чисел. Они их записывали буквами, над которыми ставили специальный значок «титло», чтобы отличить, где написали буквы, а где цифры, и значков у них было аж 27. А, например, папуасские племена имели только две цифры, один и два, и называли их «урапун» и «окоза» соответственно. А дальнейшие числа называли просто используя эти два. Например три у них — «окоза-урапун», а четыре — «окоза-окоза». Видимо, считать им особо нечего, поэтому больших чисел у них нет. А все, что больше шести-семи они называют «много». А сколько там «много» уже неизвестно! Клинопись. Но человечество развивалось, хозяйство увеличивалось, усложнялись и подсчеты. Появилась потребность в записи чисел. Ведь на память невозможно упомнить, сколько в стаде голов скота, сколько мешков пшеницы у тебя лежит, а сколько потратили, сколько посадили и какой собрали урожай. И вот примерно в V веке до нашей эры появились первые цифры. Говорят, что первые числа изобрели шумеры, народ, живший на территории Южного Междуречья Тигра и Евфрата, современного Ирака примерно в IV-III тысячелетии до н.э. Шумеры, кстати, очень интересный народ. Огромное количество изобретений, известных сейчас, были впервые использованы ими. Например, постельное белье, обожженный кирпич, колесо. Шумеры изобрели и так называемое клинописное письмо или клинопись. На глиняных табличках рисовались различные символы в виде клиньев. Цивилизация шумеров была очень развита для тех времен. В их города жили торговцы, ремесленники. Для счета применялись сначала глиняные фишки различной формы. Со временем на них стали делать пометки, которые обозначали количество и вид того, что считали. Например, две козы. Но два мешка писали совершенно по-другому. То есть они описывали количество конкретных объектов и не выделяли отдельно цифру. 
Клинописное письмо После шумеров на этих землях обосновались вавилоняне. Они переняли систему счисления шумеров. Египтяне тоже пользовались похожей системой счета. Но все-таки подобный способ записи чисел не идеален и с развитием человечества развивалась и запись чисел. Римские цифры. 
Римские цифры Римские цифры появились 500 лет до н.э. Римская система счисления была очень распространена в Европе и считалась на то время, пока не придумали арабские цифры, идеальной. I— 1 V-5 X-10 L-50 C-100 D-500 M-1000 С небольшими числами она вполне удобна, но для записи больших чисел очень сложна. Еще один недостаток: невозможно письменно делать вычисления. Их можно сделать только в уме, что, естественно, может породить большое количество ошибок. Сейчас римские цифры тоже применяют, например, в записи века, порядкового номера монарха и т.п. Арабские цифры. 
Арабские цифры В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место. 
Запись цифры по числу углов Далее произошло интересное: арабы переняли индийскую систему счисления и начали вовсю применять ее. В те времена мусульманский мир был очень развит, он имел очень тесные связи и с азиатской и европейской культурой и брал от них все самое совершенное и передовое на то время. Математик Мухаммед Аль-Хорезми в IX веке составил руководство об индийской нумерации. Оно в XII веке попало в Европу и эта система счисления получило очень широкое распространение. Интересно, но именно из-за того, что к нам эти цифры пришли от арабов, мы их называем арабскими, а не индийскими. Кстати, и само слово «цифра» — арабского происхождения. Арабы перевели индийское «сунья» и получилось «цифр». Арабская система счисления называется позиционной. Это значит, что значение числа зависит от положения его в записи. То есть в числе 18 цифра 8 обозначает 8 единиц, а в числе 87 та же восьмерка обозначает 8 десятков. Позиционные системы наиболее совершенны. Но они произошли от непозиционных систем (которые, в принципе, существуют и сейчас) в результате развития человечества, его знаний и потребностей. Интересно то, что современные арабские цифры сильно отличаются от тех, которые используем мы: 
Современные арабские цифры Вот такая история чисел. Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире. Вам также может быть интересно: История денег (с мультфильмом, который я специально для этой статьи нарисовала). История матрешки. Загрузка... lubopitnie.ru Цифры разных стран и племен. Смайлики, жабы и узелочкиВсё, о чём мы не задумываемся, кажется нам простым. Вот, например, цифры. Математика ещё может быть сложной, а цифры – это просто значки, которые обозначают числа от нуля до девяти. Нам кажется, что по-другому и быть не может! Но многие цивилизации считали иначе.Двойная жизнь букв алфавитаУ некоторых народов роль цифр традиционно исполняли буквы, каждая из которых обозначает или единицы, или десятки, или сотни и тысячи.  Например, у древних евреев 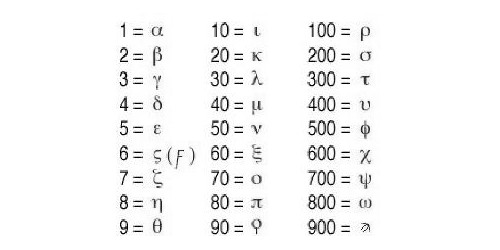 У древних греков 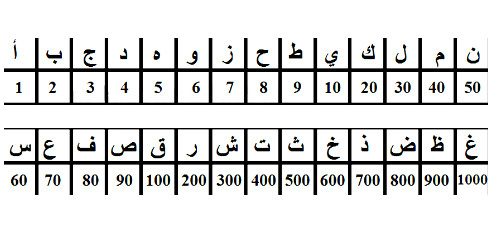 У средневековых арабов – абджадия 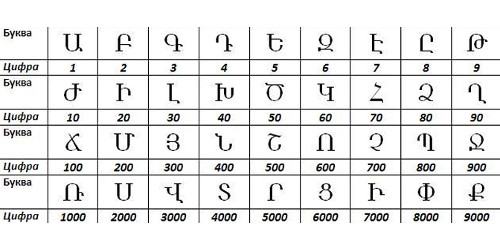 У древних армян Немного тут отличилась допетровская Русь и эфиопы; чтобы показать, что буквы надо читать именно как цифры, к ним присоединялся специальный значок. У русских он назывался “титло”:  У эфиопов  У русских Во всех этих системах записи чисел нет нуля, а многими из них нельзя записать числа больше 999. Насколько ими было удобно пользоваться для исчисления, говорит тот факт, что греческие математики записывали своими цифрами только “дано” и “ответ”, а решение выполняли пользуясь вавилонской клинописной системой. ВАВИЛОНСКОЙ КЛИНОПИСНОЙ СИСТЕМОЙ. Иначе было легче придумать новое философское учение, чем решить что-то сложнее, чем пятью пять. Весёлые картинки древних египтянУ соплеменников Тутанхамона и Нефертити было очень развитое иероглифическое письмо – того требовала не менее развитая бюрократия, однако и они не стали выделять отдельных значков под цифры. Единица обозначалась тем же иероглифом, что черта, десятка – пяткой, сотня – петлёй верёвки, тысяча – лотосом. А вот десять тысяч для европейца особенно неожиданны, потому что именно эту часть тела мы ассоциируем с жалкими единицами – палец! Сто тысяч обозначались жабой, а вот значок миллиона был уникальным. Он изображал мужчину, преклонившего колено и поднявшего руки, как бы в потрясении перед таким числом. Хотя, если вдуматься, миллион – это ведь всего лишь сто жаб или тысяча пальцев.  Сложные числа обозначались просто: значок единицы, десятка, сотни и так далее повторялся нужное количество раз, поэтому некоторые числа выглядят утомительно длинными. Да, нуля египтяне тоже не знали, но, в отличие от греков, справлялись с вычислениями как-нибудь так. С другой стороны, им было намного легче: ведь проще сложить три пальца две пятки и жабу пять лотосов, расставив их в нужном порядке вместе, чем НБ (ню бета) с ТОД (тау омикрон дельта). Сложные числа обозначались просто: значок единицы, десятка, сотни и так далее повторялся нужное количество раз, поэтому некоторые числа выглядят утомительно длинными. Да, нуля египтяне тоже не знали, но, в отличие от греков, справлялись с вычислениями как-нибудь так. С другой стороны, им было намного легче: ведь проще сложить три пальца две пятки и жабу пять лотосов, расставив их в нужном порядке вместе, чем НБ (ню бета) с ТОД (тау омикрон дельта).Смайлики от майяА вот у майя было целых два способа записывать цифры. Наверное, для скучных людей и для весёлых. В системе для скучных ноль записывался ракушкой, единица – точкой, пятёрка – линией, и этих трёх значков хватало для обозначения любого числа. Тем более, что записывались числа примерно по тому же принципу, что у нас, только система была не десятеричной, а двадцатеричной. То есть, запись точка и ракушка (10) означала наши двадцать (20). А настоящая десять записывалась как две черты (5 и 5). 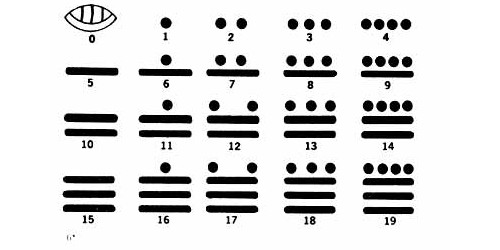 Второй способ записывать числа – иероглифы в виде голов, каждая из которых обозначает числа от 0 до 19. Причём эта система была наполовину десятеричной: начиная с 11, голова имеет чёткую приставную челюсть, как у 10. Второй способ записывать числа – иероглифы в виде голов, каждая из которых обозначает числа от 0 до 19. Причём эта система была наполовину десятеричной: начиная с 11, голова имеет чёткую приставную челюсть, как у 10. 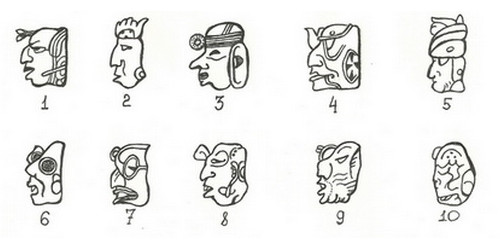  Очевидно, для вычислений использовался первый тип записи, как более наглядный, а головоцифры были только для каллиграфии по камню. Почти как с греками, только возле майя не было своих вавилонцев, чьи цифры можно было бы использовать для математических операций, и им пришлось стать самим себе вавилонцами. Очевидно, для вычислений использовался первый тип записи, как более наглядный, а головоцифры были только для каллиграфии по камню. Почти как с греками, только возле майя не было своих вавилонцев, чьи цифры можно было бы использовать для математических операций, и им пришлось стать самим себе вавилонцами.Вавилонская клинописьВавилоняне пользовались шестидесятеричной системой счисления, но внутри каждой шестидесятки она, судя по способу записи, была обычной десятеричной. Вавилоняне пользовались нулём, хотя не рассматривали его как отдельное число. Что касается непосредственно записи чисел, то от её вида немедленно начинает рябить в глазах. Мы считаем, за такой неприятный эффект вавилонские математики должны были получать молоко, а лучше пиво, потому что иначе остаться в своём уме, целый день наблюдая ЭТО, невозможно:  Древние римляне: пятёрки и десяткиНа первый взгляд, древние римляне так же, как греки, пользовались алфавитной записью чисел. На самом деле, они использовали только некоторые буквы для условного обозначения единиц и пятёрок в десятеричных разрядах. К слову, изначально часть этих цифробукв к буквам отношения не имели, это были похожие на римские буквы этрусские значки, условно обозначающие палец (I – единица), ладонь (V – пятёрка, только у этрусков она была углом кверху) и две ладони рядом (X – десять). Римляне также пользовались для обозначения чисел буквами L (50, пять десятков), C (100), D (500, пять сотен) и M (1000). Большие числа обозначали, ставя наверху буквы черту, означавшую умножение на 1000. Так, 5000 – это V (5) с чертой, 10 000 – X (10) с чертой, и так далее. 2015 год древний римлянин обозначил бы вот так: MMXV (1000+1000+10+5). При таком способе записей отдельная буквоцифра для нуля не нужна, так что и самого нуля как числа римляне не знали. Инки: узелки на памятьУ инков было два типа письменности. Классическая, узелками (“кипу”) и двумерная, в виде записей на пергаменте, листьях и даже орнаментов на одежде (“килька”). Кипу имела несколько видов сложности. Числовой записью узелками владели все взрослые инки. Простым письмом владели образованные люди (например, чиновники – инки были очень бюрократической империей), и письмом сложным, необходимым для подробных и детальных записей – только учёные и хронисты. Килька по умолчанию считалась элитным видом письменности, простым людям запрещено было ею пользоваться. Числа, как и слова, в кипу обозначались узелками определённой формы. Учёные утверждают, что инки пользовались десятеричной системой счисления и записывали числа, как мы показываем их на счётах – только вместо рядов костяшек были ряды узлов. Надо сказать, европейские цифры инки выучивали от испанцев на раз, находили их такими простыми, что аж скучно и глупо, и откровенно высмеивали. В ответ оскорблённые испанцы занимались систематическим уничтожением кипу. Так пропали многие бесценные исторические хроники. К слову, инки были первым народом, который использовал двойной счёт в бухгалтерии (записывали дебет с кредитом). Для вычислений они использовали специфический вид счёт, юпану. Некоторые современные учёные полагают, что юпана работала на фибоначчиевой системе счисления, изобретённой инками, конечно же, задолго до Фибоначчи. 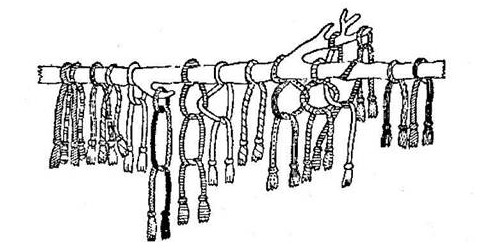 Фото: Wikimedia.Commons Текст: Лилит Мазикина pics.ru Проектная работа по алгебре на тему "Древние числа и цифры"
 Проект на тему: «Древние числа и цифры»
 Древность. В Древности у разных народов существовали свои способы счета. Например, майа использовали только три обозначения: точку, линию и эллипс и записывали ими любые цифры. В Древнем Египте около 5000-4000 лет до н.э. использовали такую запись чисел: единица обозначалась палочкой, сотня — пальмовым листом, а сто тысяч — лягушкой (в дельте Нила было очень много лягушек, вот у людей и возникла такая ассоциация: сто тысяч — очень много, как лягушек в Ниле)
 А вот наши предки-славяне использовали самую сложную запись чисел. Они их записывали буквами, над которыми ставили специальный значок «титло», чтобы отличить, где написали буквы, а где цифры, и значков у них было аж 27. А, например, папуасские племена имели только две цифры, один и два, и называли их «урапун» и «окоза» соответственно. А дальнейшие числа называли просто используя эти два. Например три у них — «окоза-урапун», а четыре — «окоза-окоза». Видимо, считать им особо нечего, поэтому больших чисел у них нет. А все, что больше шести-семи они называют «много». А сколько там «много» уже неизвестно!
 Клинопись Но человечество развивалось, хозяйство увеличивалось, усложнялись и подсчеты. Появилась потребность в записи чисел. Ведь на память невозможно упомнить, сколько в стаде голов скота, сколько мешков пшеницы у тебя лежит, а сколько потратили, сколько посадили и какой собрали урожай. И вот примерно в V веке до нашей эры появились первые цифры.
 Говорят, что первые числа изобрели шумеры, народ, живший на территории Южного Междуречья Тигра и Евфрата, современного Ирака примерно в IV-III тысячелетии до н.э. Шумеры, кстати, очень интересный народ. Огромное количество изобретений, известных сейчас, были впервые использованы ими. Например, постельное белье , обожженный кирпич, колесо. Шумеры изобрели и так называемое клинописное письмо или клинопись. На глиняных табличках рисовались различные символы в виде клиньев. Цивилизация шумеров была очень развита для тех времен. В их города жили торговцы, ремесленники. Для счета применялись сначала глиняные фишки различной формы.
 Римские цифры.
 Римские цифры появились 500 лет до н.э. Римская система счисления была очень распространена в Европе и считалась на то время, пока не придумали арабские цифры, идеальной. I— 1 V-5 X-10 L-50 C-100 D-500 M-1000
 Арабские цифры.
 В V веке в Индии появилась система записи, которую мы знаем как арабские цифры и активно используем сейчас. Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
 Далее произошло интересное: арабы переняли индийскую систему счисления и начали вовсю применять ее. В те времена мусульманский мир был очень развит, он имел очень тесные связи и с азиатской и европейской культурой и брал от них все самое совершенное и передовое на то время. Арабская система счисления называется позиционной. Это значит, что значение числа зависит от положения его в записи. То есть в числе 18 цифра 8 обозначает 8 единиц, а в числе 87 та же восьмерка обозначает 8 десятков. Позиционные системы наиболее совершенны. Но они произошли от непозиционных систем (которые, в принципе, существуют и сейчас) в результате развития человечества, его знаний и потребностей
 Интересно то, что современные арабские цифры сильно отличаются от тех, которые используем мы:
 Завершение: Вот такая история чисел . Сейчас тоже используются разные числа. Некоторые страны, как например, арабские страны и Китай, пользуются своими особенными цифрами. Но, все-таки, наибольшее распространение получили арабские цифры, которые используют и понимают во всем мире.
 СПАСИБО ЗА ВНИМАНИЕ! compedu.ru Правдивая история возникновения чиселЧисла преследуют человека везде. Даже наше тело созвучно их миру – мы имеем определенное количество органов, зубов, волос и кожных клеток. Счет стал привычным, автоматическим действием, поэтому сложно представить, что когда-то люди не знали цифр. На самом деле история возникновения чисел прослеживается с самых древних времен. Числа и первобытные людиВ какой-то момент человек ощутил большую потребность в счете. На это его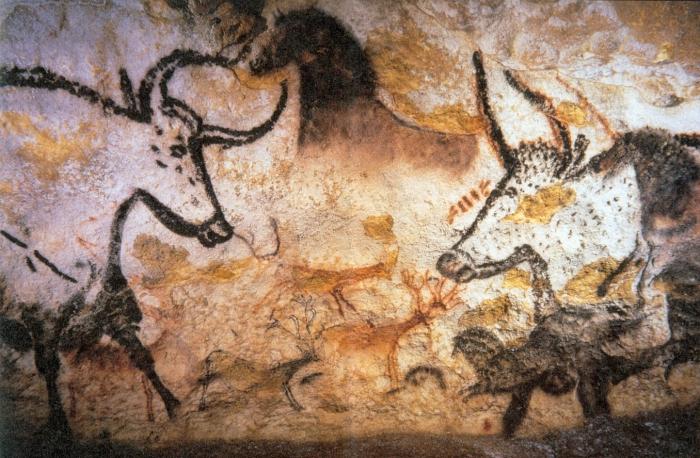 подтолкнула сама жизнь. Необходимо было каким-то образом организовывать племя, отправляя на охоту или собирательство только определенное количество человек. Поэтому для счета пользовались пальцами на руках. До сих пор есть племена, которые вместо цифры «5» показывают одну руку, а вместо десяти – две. С такого простого алгоритма счета и начала развиваться история возникновения чисел. подтолкнула сама жизнь. Необходимо было каким-то образом организовывать племя, отправляя на охоту или собирательство только определенное количество человек. Поэтому для счета пользовались пальцами на руках. До сих пор есть племена, которые вместо цифры «5» показывают одну руку, а вместо десяти – две. С такого простого алгоритма счета и начала развиваться история возникновения чисел. Чтобы посчитать 40 оленей, первобытному человеку надо было всего лишь позвать одного соплеменника. Но эта система счисления становилась необычайно сложной, если речь шла о большем количестве предметов или животных. Поэтому до возникновения чисел широкое распространение получили зарубки на стенах, камнях, прочих предметах. Иногда они получались слишком длинными и громоздкими, что подтолкнуло к новой идее – придумать символы, каждый из которых будет отвечать за определенное количество чего-либо. Числа и древностьВозникновение чисел происходило у каждого этноса по-особенному. Так, древний  народ майя использовал рисунки страшных голов вместо привычных нашему глазу цифр. народ майя использовал рисунки страшных голов вместо привычных нашему глазу цифр. Принято считать, что создание знакомых нам цифр – заслуга арабов. Само слово «цифра» пришло к нам в язык от арабского «сыфр» (в буквальном переводе «пустое место»). Трактаты о числах в Европе были переведены именно с арабского языка, но они всего лишь послужили повсеместному распространению десятичной системы счисления. Истинной родиной обычной нумерации стала Индия. На всей территории этой страны было распространено множество различных вариаций записи цифр, но в какой-то момент из общей массы выделился тот, который мы используем до сих пор. Числа имели вид точно такой же, как первые буквы в их названиях на санскрите. Впоследствии, чтобы указать пустой разряд, ввели точку или жирный кружок, более известный нам как «ноль». Именно тогда система счисления превратилась в десятичную. С этого момента берет начало история возникновения натуральных чисел. 
Простые числаИстория возникновения чисел позволяет заметить, что люди довольно давно обнаружили разницу между нечетной и четной цифрой, а также различные взаимосвязи внутри самих числовых выражений. Немалый вклад в подобные исследования внесли древние греки. Например, греческий ученый Эратосфен создал довольно легкий способ поиска простых чисел. Для этого он записывал нужное количество цифр по порядку, а потом начинал вычеркивать – сначала все числа, которые можно делить на два, потом – на три. В результате получался список цифр, которые ни на что не делятся, кроме единицы и себя самого. Этот метод был назван «решето Эратосфена» из-за того, что греки не вычеркивали, а выкалывали ненужные числа на табличках, покрытых воском. Таким образом, история возникновения чисел – явление древнее и глубинное. По оценкам ученых, оно началось еще около 30 тысяч лет назад. За это время в жизни человека успело поменяться многое. Но магия числа и по сей день руководит нашим бытием. fb.ru Цифры разных народов Протокол проведения исследования ГЛАВА 1. Что такое число? Всё, о чём мы не задумываемся, кажется нам простым. Вот, например, цифры. Математика ещё может быть сложной, а цифры – это просто значки, которые обозначают числа от нуля до девяти. Нам кажется, что по-другому и быть не может! Но многие цивилизации считали иначе. Числа были всегда и 4 и 5 тысяч лет тому назад, только правила изображения их былидругими.Носмыслбылодин:числаизображалисьспомощью определённых знаков– цифр.Цифра- это символ, участвующий в записи числа. Число- это величина, которая складывается из цифр по определённым правилам. Эти правила называются системами счисления[1]. До появления числовых обозначений — цифр и букв, с которыми мы сейчас ассоциируем число, наши ранние предки пользовались «эталонами», которые они выбирали по ассоциативному принципу. Например, все знали, что Луна на небе одна, рук (или глаз) у человека две, а пальцев на каждой руке по пять. Поэтичные отголоски такой системы можно отыскать сейчас в раннем словесном счете индусов, где единицу называли Землей, Луной, Брахмой; двойку — «близнецами», «глазами»; пятерку — «чувствами» и так далее. Позднее древние окончательно определились, что считать нужно тем, чего много и что всегда при себе, и выбрали пальцы, поэтому подавляющее большинство систем счисления основано на принципе счета по десяткам (по количеству пальцев на обеих руках). Из существующих ныне исключений из этого правила можно вспомнить французский язык, где счет ведется двадцатками: 80 — quatre-vingts (4*20), 90 — quatre-vingt-dix (4*20+10). Но и здесь двадцать — это общее количество пальцев на руках и ногах. Напротяжениимноговековойисториичеловечествасуществовало множество различных способов записи числа, некоторые дошли до наших времен, а некоторые остались в истории. Несколькодесятковлетназадучёные-археологиобнаружилистойбище древнихлюдей.Внёмонинашливолчьюкость,накоторой30тысячлеттому назадкакой-тоохотникнанёс55зарубок.Видно,что,делаяэтизарубки,он считал по пальцам. Узор на кости состоял из 11 групп, по 5 зарубок в каждой. При этом первые 5 групп он отделил от остальных длинной чертой. Позднее в Сибири и других районах были найдены сделанные в ту далекую эпоху каменного века(каменные)кораблекрушения,на которых тоже были черточки и точки,сгруппированные по 3, по 5, или по 7. ГЛАВА 2. Цифры древних цивилизаций Цифры в Древнем Египте Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находилисьдалекооднаотдругой,ихчисловыесистемыоченьпохожи: использованиезасечекна деревеиликамнедлязаписипрошедшихдней. Египетские жрецы писали на папирусе, изготовленном из стеблей определенных сортов тростника, а в Месопотамии на мягкой глине. Вегипетскойсистемецифрами являлисьиероглифические символы; Единица обозначалась тем же иероглифом, что черта, десятка – пяткой, сотня – петлёй верёвки, тысяча – лотосом. А вот десять тысяч для европейца особенно неожиданны, потому что именно эту часть тела мы ассоциируем с жалкими единицами – палец! Сто тысяч обозначались жабой, а вот значок миллиона был уникальным. Он изображал мужчину, преклонившего колено и поднявшего руки, как бы в потрясении перед таким числом. Хотя, если вдуматься, миллион – это ведь всего лишь сто жаб или тысяча пальцев. Числа,некратные10,записывалисьпутемповторенияэтихцифр.Каждая цифра могла повторяться от одного до 9 раз. Цифры племени майя А вот у майя было целых два способа записывать цифры. Наверное, для скучных людей и для весёлых. В системе для скучных ноль записывался ракушкой, единица – точкой, пятёрка – линией, и этих трёх значков хватало для обозначения любого числа. Тем более, что записывались числа примерно по тому же принципу, что у нас, только система была не десятеричной, а двадцатеричной. То есть, запись точка и ракушка (10) означала наши двадцать (20). А десять записывалась как две черты (5 и 5). Второй способ записывать числа – иероглифы в виде голов, каждая из которых обозначает числа от 0 до 19. Причём эта система была наполовину десятеричной: начиная с 11, голова имеет чёткую приставную челюсть, как у 10. Очевидно, для вычислений использовался первый тип записи, как более наглядный, а головоцифры были только для каллиграфии по камню. Такиецифрыиспользовалиськрайнередко,сохранившисьлишьна нескольких монументальных стелах. Цифры инков У инков было два типа письменности. Классическая, узелками (“кипу”) и двумерная, в виде записей на пергаменте, листьях и даже орнаментов на одежде (“килька”). Кипу имела несколько видов сложности. Числовой записью узелками владели все взрослые инки. Простым письмом владели образованные люди (например, чиновники – инки были очень бюрократической империей), и письмом сложным, необходимым для подробных и детальных записей – только учёные и хронисты. Килька по умолчанию считалась элитным видом письменности, простым людям запрещено было ею пользоваться. Числа, как и слова, в кипу обозначались узелками определённой формы. Учёные утверждают, что инки пользовались десятеричной системой счисления и записывали числа, как мы показываем их на счётах – только вместо рядов костяшек были ряды узлов. Во время испанской и португальской колонизации Южной Америки испанцы занимались систематическим уничтожением кипу. Так пропали многие бесценные исторические хроники. Инки были первым народом, который использовал двойной счёт в бухгалтерии (записывали дебет с кредитом). Для вычислений они использовали специфический вид счёта, юпану. Некоторые современные учёные полагают, что юпана работала на фибоначчиевой системе счисления, изобретённой инками, задолго до Фибоначчи. Вавилонская клинопись Вавилоняне пользовались шестидесятеричной системой счисления, но внутри каждой шестидесятки она, судя по способу записи, была обычной десятеричной. Вавилоняне, славились своими астрономическими наблюдениями и расчётами (с помощью своего изобретения абака). Они унаследовали эту систему счисления от шумерской и аккадской цивилизаций. Она применялась за две тысячи лет до н. э. Для записи чисел использовались всего два знака: прямой клин для обозначения единиц и лежачий клин для обозначения десятков внутри шестидесятеричного разряда. Новый шестидесятеричный разряд начинался с появлением прямого клина после лежачего клина, если рассматривать число справа налево. Вавилоняне пользовались нулём, хотя не рассматривали его как отдельное число: Вначале нуля не было. Позже ввели обозначение для пропущенных шестидесятеричных разрядов, что соответствует появлению нуля Цифры Древней Греции ВДревнейГрецииимелихождениедвеосновныхсистемысчисления- аттическая(илигеродианова)иионическая(онажеалександрийскаяили алфавитная). Аттическая система счисления — непозиционная система счисления, применявшаяся в древней Греции до III века до н. э. Она употребляет в качестве цифр греческие буквы, причём цифрами служили первые буквы слов, которые обозначали соответствующие числа. Черта, обозначавшаяединицу,повтореннаянужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Π, первую букву слова "пента» (пять). Дойдя до десяти,они ввели еще один новый символ Δ, первую букву слова "дека»(десять). | знак | значение | название | | Ι | 1 | ἴος «иос» | | Π | 5 | πέντε «пенте» | | Δ | 10 | δέκα «дека» | | Η | 100 | ἑκατόν «хекатон» | | Χ | 1 000 | χίλιοι «хилиой» | | Μ | 10 000 | μύριοι «мириой» |
Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ Hозначал100(хекатон),X- 1000(хилиой),символM- 10000(мириойили мириада).Числа6,7,8,9обозначалисьсочетаниямиэтихзнаков. При записи чисел сначала записывали большие числа, потом — меньшие. Например, ΗΔΔΠΙΙΙ - 128 Χ MMΠΔΔΔΔ - 25 040 Принцип записи чисел в аттической системе счисления имеет значительное сходство с римской системой. Это может быть связано с влиянием восточносредиземноморских культур на этрусков, у которых римляне позаимствовали систему счисления. После III века до н.э. аттическая система счисления была вытеснена ионийской. Ионийская или новогреческая — непозиционная система счисления. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϛ (стигма), ϟ (коппа) и ϡ (сампи). | 1 α | 10 ι | 100 ρ | | 2 β | 20 κ | 200 σ | | 3 γ | 30 λ | 300 τ | | 4 δ | 40 μ | 400 υ | | 5 ε | 50 ν | 500 φ | | 6 ϝ или ϛ | 60 ξ | 600 χ | | 7 ζ | 70 ο | 700 ψ | | 8 η | 80 π | 800 ω | | 9 θ | 90 ϟ | 900 ϡ |
Данные символы позволяют записать лишь целые числа от 1 до 999, например: - 45 — με
- 632 — χλβ
- 970 — ϡο
Необходимость сохранять порядок букв ради сохранения их числовых значений привела к относительно ранней (4 век до н. э.) стабилизации греческого алфавита. Цифры Древнего Китая Этанумерацияоднаизстарейшихисамыхпрогрессивных. Возниклаона около 4 000 тысяч лет тому назад в Китае. Хотя в повседневном использовании китайские числа постепенно вытесняются арабскими цифрами, тем не менее, они продолжают широко применяться. Существует два набора символов — обычная запись для повседневного использования и формальная запись, используемая в финансовом контексте Записывалисьцифрычисланачинаясбольшихзначенийизаканчивая меньшими.Еслидесятков,единиц,иликакого-тодругогоразряданебыло,то сначаланичегонеставилиипереходиликследующемуразряду.(Вовремена династииМинбылвведензнакдляпустогоразряда- кружок- аналогнашего нуля).Чтобынеперепутатьразрядыиспользовалинесколькослужебных иероглифов,писавшихсяпослеосновногоиероглифа,ипоказывающихкакое значение принимает иероглиф-цифра в данном разряде. Славянская кириллическая нумерация Этаформазаписичиселимелаполноесходствосгреческойзаписьючисел.Еслипосмотреть внимательно, то увидим, что после «а» идет буква «в», а не «б» как следует по славянскому алфавиту, то есть используютсятолькобуквы,которыеестьв греческом алфавите. Чтобыразличатьбуквыицифры,надчислами ставился особый значок —титло ( ~ ) Римская нумерация Римские цифры появились за 500 лет до нашей эры у этрусков, которые могли заимствовать часть цифр у прото-кельтов. Древнеримскаясистемасчисления, основана на использовании букв для отображения цифр.Каждаябукваимеларазличноезначение,каждая цифра соответствовала номеру положения буквы Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая стоит перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Горизонтальная линия над буквой увеличивает её значение в 1000 раз. Например, _____ ____ V означает 5000, CIII - 103000 и IXDL - 9550. Несмотря на то, что латынь называют «мертвым» языком, латинские цифры нашли применение и в наше время в документоведении, оформлении научных работ. Доступность, понятность и четкость сделали их завсегдатаями учебников и рефератов. ГЛАВА 3. История возникновения арабских цифр После крушения Римской империи наиболее влиятельной цивилизацией в средневековой Европе стала арабская. Исламские ученые VIII–XII веков переводили древнегреческие и латинские трактаты по математике, медицине, философии, физике и с помощью них далеко продвинулись в науках. В начале IX века среднеазиатский ученый Аль-Хорезми впервые выделил алгебру как самостоятельную науку («ал-горитм» — это переработанное на современный манер имя ученого, а слово «ал-джебр» впервые фигурировало в названии его сочинения). В таких условиях искусство счета совершило невероятный скачок, и в нумерации впервые возникло понятие числа «нуль» (по арабски «сыфыр» — пустой, ничто), с которым пришел и принцип позиционной системы счисления, которым мы пользуемся поныне. Эта числовая реформа совершила настоящую революцию в науке: ведь теперь вместо громоздких конструкций появились знакомые каждому школьнику лаконичные цифровые обозначения, с помощью которых очень удобно производить математические расчеты. При этом называть современные цифры арабскими будет большой исторической несправедливостью, ведь родились они в Индии и назывались «деванагари» (божественное письмо). Индийско-арабскую систему счисления взяли на вооружение европейские ученые, когда в XII веке начали активно переводить арабских авторов на латинский язык. Распространению новой системы счета способствовало то, что начиная в XIV века в Европе стало открываться много светских школ, готовящих торговцев. С середины XV века новые цифры активно фигурировали на европейских монетах разных стран и именно тогда вошли в широкий обиход. Неважно, откуда берет истоки история возникновения чисел, главное, они стали достоянием всего мира. Цифры легко пишутся и запоминаются, что облегчает и смысловое восприятие. Ведь перед нами не длинная вереница закорючек и букв. Системы счисления «Наша система счисления имеет три основных характеристики:она позиционная, аддитивная и десятичная. -Позиционная,поскольку каждая цифра имеет определенное значение согласно ее месту,занимаемое в ряду,выражающем числом:2 означает две единицы в числе 52 и двадцать единиц в числе 25. - Аддитивная, или слагаемая, поскольку значение одного числа равно сумме значений цифр, образующих его. Так, значение 52 равно сумме 50+2. -Десятичная, поскольку каждый раз, одна цифра смещается на одно место Влево в написании числа, его значение увеличивается в десять раз. Так, число 2, имеющее значение две единицы,превращаетсявдвадцатьединицвчисле26, поскольку перемещается на одно место влево. Арабская позиционная нумерация, которой мы пользуемся сегодня, очень проста в записи, с ее помощью удобно считать. Но не все системы счисления могли этим похвастаться. Уже упомянутая египетская система счисления была аддитивной: единицы, десятки, сотни, тысячи (и выше) имелись свои изображения, которые при записи ставились в ряд друг за другом, а число получалось путем простого прибавления цифр. К примеру, это на самом деле является египетской записью числа 2334: По аддитивному принципу была выстроена и греческая нумерация, заимствованная нашими древнерусскими предками, а также народами древней Грузии и Армении. Древнерусская запись числительных велась с помощью букв кириллицы или глаголицы. То есть кириллическая запись числа 217 выглядела бы как простая запись букв С I З, а на глаголице — вот так: Римская нумерация — наиболее простой пример субстративного метода, смешанного с аддитивным. Здесь цифры как прибавляются друг к другу, так и вычитаются друг из друга: MXCVIII — это 1000+(100-10)+5+3=1098. Сравнение записи цифр у разных народов При изучении записи цифр у разных народов, я пришел к выводу, что цифры большинства из них похожи.При записи чисел во всех,кроме древнекитайской системы счисления,используется аддитивный способ. В Китае– мультипликативная система счисления. ЗАКЛЮЧЕНИЕ Изучая данный вопрос я пришел к выводу, что: Числа появились в древние времена (около 5000 лет назад). Изучив историю возникновения цифр, я узнал, что арабские цифры были заимствованы арабами в Индии. Они передали данный способ записи в Европу. Таким образом, моя гипотеза, что способы записи чисел у разных народов схожи частично подтвердилась. Я научился изображать цифры теми способами, которыми пользовались наши предки. В ходе исследования, проанализировав указанные факты и взаимосвязь между ними, мне стало понятно,что история чисел и системы счисления не могут рассматриваться раздельно. Системы счисления формировались одновременно с числами. Культурная, экономическая, политическая ситуация каждого государства создала условия для их формирования, что объясняет различия между системами счисления. В заключение могу сказать, что в разных системах счисления есть схожие элементы, например, наличие нуля (как в Древнекитайской десятеричной системе счисления и двадцатеричной системе счисления индейцев Майя), счет путем добавления палочек (как в Древнеегипетской десятеричной, Римской пятеричной и Древнегреческой аттической пятеричной системах счисления), замена чисел на алфавитные символы с добавлением титлы (как в Древнегреческой ионийской десятеричной алфавитной и Славянской кириллической десятеричной алфавитной системах счисления). Исследуя системы счисления Древнего мира, я сделал вывод, что каждая из систем имеет свои недостатки. На мой взгляд человечество выбрало самый эффективный и удобный метод счета с помощью арабской системы счисления. Работать над темой мне понравилось. В дальнейшем я хотел бы рассмотреть вопросы: почему те или иные цифры получили именно такие названия, какой магический смысл вкладывался в каждую из цифр и многое другое. globallab.org История развития числа. Развитие понятия числаРазвитие представлений о числе составляет важную часть нашей истории. Оно является одним из основных математических понятий, которое позволяет выразить результаты измерения или счета. Исходным для множества математических теорий служит понятие числа. Оно применяется также в механике, физике, химии, астрономии и множестве других наук. Кроме того, в повседневной жизни мы постоянно пользуемся числами. 
Появление цифрПоследователи учения Пифагора считали, что числа содержат в себе мистическую сущность вещей. Эти математические абстракции руководят миром, устанавливая порядок в нем. Пифагорейцы предполагали, что все существующие в мире закономерности можно выразить с помощью чисел. Именно с Пифагора теория развития чисел стала интересовать множество ученых. Символы эти считались основой материального мира, а не просто выражениями некоторого закономерного порядка. 
История развития числа и счета началась с того, что был создан практический счет предметов, а также измерения объемов, поверхностей и линий. Постепенно формировалось понятие о натуральных числах. Этот процесс осложнялся тем, что первобытный человек не умел отделять от конкретного представления абстрактное. Счет в результате этого оставался долгое время лишь вещественным. Использовались пометки, камешки, пальцы и т. п. Применяли для запоминания его результатов узелки, зарубки и пр. После изобретения письменности история развития числа была отмечена тем, что начали использовать буквы, а также особые значки, применявшиеся для сокращенного изображения на письме больших чисел. Обычно воспроизводился при таком кодировании принцип нумерации, аналогичный использовавшемуся в языке. Позднее появилась идея считать десятками, а не только единицами. В 100 различных индоевропейских языках названия чисел от двух до десяти сходны, как и названия десятков. Следовательно, очень давно появилось понятие абстрактного числа, еще до того, как языки эти были разделены. Счет по пальцам первоначально был широко распространен, и это объясняет то, что у большинства народов при образовании числительных особое положение занимает символ, обозначающий 10. Десятичная система счисления происходит именно отсюда. Хотя существуют и исключения. Например, 80 в переводе с французского языка - "четыре двадцатки", а 90 - "четыре двадцатки плюс десять". Употребление это восходит к счету по пальцам ног и рук. Устроены аналогично числительные абхазского, осетинского и датского языков. В грузинском языке счет двадцатками еще яснее. Ацтеки и шумеры считали первоначально пятерками. Существуют также и более экзотические варианты, которыми отмечена история развития числа. Например, в научных расчетах вавилоняне применяли шестидесятеричную систему. В так называемых "унарных" системах число образуется с помощью повторения знака, символизирующего единицу. Древними людьми такой способ применялся примерно 10-11 тыс. лет до н. э. Существуют также непозиционные системы, в которых количественные значения используемых для записи символов не зависят от их места в коде числа. Используется сложение цифр. Древнеегипетские числа
Знание математики Древнего Египта основано сегодня на двух папирусах, которые датируются приблизительно 1700 годом до н. э. Математические сведения, излагаемые в них, восходят к более древнему периоду, около 3500 года до н. э. Египтяне эту науку использовали для того, чтобы вычислять вес различных тел, объемы зернохранилищ и площади посевов, размеры податей, а также необходимое для возведения сооружений количество камней. Однако основной областью применения математики была астрономия, связанные с календарем расчеты. Календарь необходим был для определения дат различных религиозных праздников, а также предсказания разливов Нила. Письменность в Древнем Египте была основана на иероглифах. В тот период система счисления уступала вавилонянской. Пользовались египтяне непозиционной десятичной системой, в которой количеством вертикальных черт обозначались числа от 1 до 9. Индивидуальные символы вводились для степеней десяти. История развития числа в Древнем Египте продолжилась следующим образом. С возникновением папируса было введено иератическое письмо (то есть скоропись). Специальный символ использовался в нем для обозначения чисел от 1 до 9, а также кратных 10, 100 и т. д. Развитие рациональных чисел в то время происходило медленно. Они записывались, как сумма дробей с равным единице числителем. Числа в Древней ГрецииНа использовании различных букв алфавита была основана греческая система счисления. История натуральных чисел в этой стране отмечена тем, что употреблявшаяся с 6-3 веков до н. э. аттическая система для обозначения единицы применяла вертикальную черту, а 5, 10, 100 и т. д. писались с помощью начальных букв их названий на греческом языке. В ионической системе, более поздней, использовались для обозначения чисел 24 действующие буквы алфавита, а также 3 архаические. Как первые 9 чисел (от 1 до 9) обозначались кратные 1000 до 9000, однако перед буквой ставилась при этом вертикальная черта. "М" обозначались десятки тысяч (от греческого слова "мириои"). После нее следовало число, на которое следовало умножить 10000. 
В Греции в 3 веке до н. э. возникла числовая система, в которой собственный знак алфавита соответствовал каждой цифре. Греки, начиная с 6 века, в качестве цифр стали использовать первые десять знаков своего алфавита. Именно в этой стране не только активно развивалась история натуральных чисел, но и зародилась математика в современном ее понимании. В других государствах того времени она применялась либо для обыденных нужд, либо для различных магических ритуалов, с помощью которых выясняли волю богов (нумерология, астрология и т. п.). Римская нумерация
В Древнем Риме использовалась нумерация, которая под именем римской сохранилась и до сегодняшних дней. Мы ее применяем для обозначения юбилейных дат, веков, наименования конференций и съездов, нумерации строф стихотворения или глав книги. С помощью повторения цифр 1, 5, 10, 50, 100, 500, 1000, обозначавшихся у них, соответственно, как I, V, X, L, C, D, M записываются все целые числа. Если большая цифра находится перед меньшей, они суммируются, если же перед большей стоит меньшая, то последняя вычитается из нее. Одну и ту же цифру нельзя ставить более трех раз. Долгое время страны Западной Европы пользовались в качестве основной римской нумерацией. Позиционные системыЭто такие системы, в которых количественные значения символов зависят от их места в коде числа. Основные их достоинства - простота выполнения различных арифметических операций, а также небольшое число символов, необходимых для записи чисел. Достаточно много существует таких систем. Например, двоичная, восьмеричная, пятеричная, десятичная, двадцатеричная и др. Каждая имеет собственную историю. Система, существовавшая у инков
Кипу - это древняя счетная и мнемоническая система, которая существовала у инков, а также их предшественников в Андах. Она довольно своеобразна. Это сложные узелки и веревочные сплетения, изготовленные из шерсти лам и альпак, либо из хлопка. Может быть в кипу от нескольких свисающих нитей до двух тысяч. Использовалась она посыльными для передачи сообщений по имперским дорогам, а также в различных аспектах жизни общества (как топографическая система, календарь, для фиксации законов и налогов и др.). Читали и писали кипу толкователи, специально обученные. Они ощупывали узелки пальцами, беря в руки кипу. Большая часть информации в ней - числа, представленные в десятичной системе. 
Вавилонские цифрыНа глиняных табличках клинописными значками писали вавилоняне. Они дошли до наших дней в немалом количестве (более 500 тыс., около 400 из которых связаны с математикой). Следует отметить, что корни культуры вавилонян были унаследованы в значительной степени от шумеров - счетная методика, клинописное письмо и т. п. Намного совершеннее египетской была вавилонская система счета. Вавилоняне и шумеры применяли 60-ричную позиционную, которая сегодня увековечена в делении круга на 360 градусов, а также часа и минуты на 60 минут и секунд соответственно. Счет в Древнем КитаеРазвитие понятия о числе осуществлялось и в Древнем Китае. В этой стране цифры обозначались с помощью специальных иероглифов, появившихся примерно 2 тыс. лет до н. э. Однако окончательно начертание их установилось лишь к 3 веку до н. э. И сегодня применяются эти иероглифы. Сначала мультипликативным был способ записи. Число 1946, например, можно представить, используя римские цифры вместо иероглифов, как 1М9С4Х6. Но расчеты на практике производились на счетной доске, где была иной запись чисел - позиционной, как в Индии, а не десятичной, как у вавилонян. Пустым местом обозначался нуль. Лишь около 12 века н. э. появился для него специальный иероглиф. История счисления в ИндииМногообразны и широки достижения математики в Индии. Эта страна внесла большой вклад в развитие понятия о числе. Именно здесь была изобретена десятичная позиционная система, привычная нам. Индийцы предложили символы для записи 10 цифр, с некоторыми изменениями использующиеся в наши дни повсеместно. Именно в этой стране были заложены также основы десятичной арифметики. Современные цифры произошли от индийских значков, начертание которых использовалось еще в 1 веке н. э. Изначально индийская нумерация была изысканной. Средства для записи чисел до десяти в пятидесятой степени применялись в санскрите. Сначала для цифр использовалась так называемая "сиро-финикийская" система, а с 6 века до н. э. - "брахми", с отдельными знаками для них. Эти значки, несколько видоизменившись, стали современными цифрами, называемыми сегодня арабскими. Неизвестный индийский математик примерно в 500 году н. э. изобрел новую систему записи - десятичную позиционную. Выполнение различных арифметических действий в ней было неизмеримо проще, чем в других. Индийцы в дальнейшем применяли счетные доски, которые были приспособлены к позиционной записи. Ими были разработаны алгоритмы арифметических операций, в том числе получения кубических и квадратных корней. Индийский математик Брахмагупта, живший в 7-м веке, ввел в употребление отрицательные числа. Далеко продвинулись индийцы в алгебре. Символика их более богата, чем у Диофанта, хотя несколько засорена словами. Историческое развитие чисел на РусиНумерация служит главной предпосылкой математических знаний. Она имела разный вид у различных народов древности. Возникновение и развитие числа на раннем этапе совпадало в различных частях света. Сначала все народы обозначали их зарубками на палочках, называвшихся бирками. Этот способ записи налогов или долговых обязательств использовался малограмотным населением всего мира. Делали нарезы на палочке, которые соответствовали сумме налога или долга. Затем ее раскалывали пополам, оставив одну половину у плательщика или должника. Другая хранилась в казначействе или у заимодавца. Обе половинки при расплате проверяли складыванием. Цифры появились с возникновением письменности. Они напоминали сначала зарубки на палках. Потом появились специальные значки для некоторых из них, таких как 5 и 10. Все нумерации в то время были не позиционными, а напоминающими римскую. В Древней Руси, в то время как в государствах Западной Европы применяли римскую нумерацию, пользовались алфавитной, сходной с греческой, так как наша страна, подобно другим славянским, как известно, находилась в культурном общении с Византией. Числа от 1 до 9, а потом десятки и сотни в древнерусской нумерации изображались буквами славянского алфавита (кириллицы, введенной в девятом веке). 
Некоторые исключения были из этого правила. Так, 2 обозначалось не "буки", второй по счету в алфавите, а "веди" (третьей), поскольку буква З по-старорусски передавалась звуком "в". Находившаяся в конце алфавита "фита" обозначала 9, "червь" - 90. Отдельные буквы не использовались. Для обозначения того, что знак этот является цифрой, а не буквой, над ним сверху писали знак, называемый "титло", «~». "Тьмы" назывались десятки тысяч. Обозначали их, обводя кружками знаки единиц. Сотни тысяч именовались "легионами". Их изображали, кружками из точек обводя знаки единиц. Миллионы - "леодры". Эти знаки изображались как обведенные в кружки из запятых или лучей. Дальнейшее развитие натурального числа произошло в начале семнадцатого века, когда индийские цифры стали известны на Руси. Вплоть до восемнадцатого века использовалась в России славянская нумерация. После этого она была заменена современной. История комплексных чиселЭти числа были введены впервые в связи с тем, что была выделена формула вычисления корней кубического уравнения. Тартальей, итальянский математик, получил в первой половине шестнадцатого века выражение расчета для корня уравнения через некоторые параметры, для нахождения которых нужно было составить систему. Однако было выяснено, что подобная система имела решение не для всех кубических уравнений в действительных числах. Это явление объяснил Рафаэль Бомбелли в 1572 году, что было по сути введением комплексных чисел. Однако полученные результаты долгое время считались сомнительными многими учеными, и лишь в девятнадцатом веке история комплексных чисел ознаменовалась важным событием - их существование было признано после появления трудов К. Ф. Гаусса. fb.ru
|
