Как считали в разных странах с начала времён. Цифры древние
Что из себя представляли вавилонские числа?Математика, как наука, обязана своим появлением Древнему Востоку. Нет точных дат ее зарождения, но достоверно известно, что практически каждое отдельно взятое восточное государство имело свою систему исчисления и методы расчета. В данной статье мы обсудим такое явление, как вавилонские числа, рассмотрим археологические артефакты, подтверждающие их существование, и оценим их влияние на дальнейшее развитие науки. 
ВступлениеВавилонское царство начало свое существование во II тысячелетии, а пало в 539 году до нашей эры. За этот период данный восточный регион сделал серьезный шаг вперед во многих сферах жизни, уделив особое внимание архитектуре и астрономии. Но для того, чтобы постройки были устойчивыми и долговечными, чтобы наблюдения за небесными светилами можно было записать и проанализировать, требовалась математика. Поэтому на заре зарождения новой цивилизации в Месопотамии появились и новые вавилонские числа. Так как государство строилось на обломках некогда существовавших здесь Шумера и Аккада, также весьма могущественных держав, изобретения и научные достижения предшественников помогли вавилонянам стать развитой и прогрессирующей расой. 
Система счисления Вавилонского царстваПри первом взгляде на вавилонские числа сразу возникает ассоциация с римскими, так как принцип их записи практически идентичен, и при этом куда более простой. В системе используется всего два знака: прямой клинок, обозначающий единицы, и лежачий клинок, который оценивают в десяток. Для записи цифр от 1 до 9 используется только первый символ, а для всех последующих показателей применяется та или иная комбинация двух клиньев. Важно отметить, что система счисления была шестидесятеричной и делилась на соответствующие разряды, и это неслучайно. Шестеричным делением Вавилон обязан шумерам, а наличием десятка – аккадцам. В дальнейшем вавилонские числа продублированы арабскими, римскими и греческими и стали основой времяисчисления. С тех пор мы делим час на 60 минут, а каждую минуту на 60 секунд. 
Трудности в вавилонской математикеКак мы видим на таблице, числовой ряд в Древнем Вавилоне оканчивался на 59, так как система была шестидесятеричной. Но ведь столь развитая цивилизация не могла ограничиваться лишь таким объемом цифр? Совершенно верно. Вавилонская нумерация чисел предполагала огромные показатели, которые сегодня мы называем трех-, четырех- и пятизначными. Как пример возьмем отрезок от 60 до 120. Для цифры 60 применялся тот же клинок, что и для единицы, только большего размера. После него оставляли большой пробел и далее записывали остальную часть числа. Это со временем стало порождать путаницу, с которой порой не могли разобраться даже сами древние пользователи. Можно только гадать, как ломали мозг эксперты, которые расшифровывали подобные артефакты. Кроме того, вавилоняне не имели нуля, а это значительно упростило бы запись сложных чисел. 
От путаницы к порядкуЧтобы узнать вавилонские числа в ряде других систем исчисления, достаточно запомнить два знака. Чтобы правильно прочитать их и определить значение, необходимо ознакомиться с принципом позиционности. Для нас в этом нет ничего сложного, так как в современном мире существует единая позиционная система. Суть ее заключается в том, что место той или иной цифры влияет на значимость числа. Согласитесь, если мы меняем местами 1 и 7 в числе 17, то результат становится совсем иным. Но для древних народов это не было столь очевидным, так как ранее позиция цифры в числе не имела значения. Вавилоняне первыми в истории человечества поняли, что нет необходимости создавать множество знаков, записывая их хаотично. Достаточно будет двух, значение которых будет зависеть от позиции. Вавилонские «тетрадки»В государствах между Тигром и Евфратом не только правители, но и простые люди были весьма образованными, но для полной гармонии им не хватало одного элемента – бумаги. В Египте вместо нее использовали папирус, на котором рисовали древние иероглифы и значки, а вавилонская запись чисел и букв-картинок велась на глиняных табличках. 
Такая техника называется клинописью, и суть ее заключается в том, что пока глина мягкая, заточенным деревянным клинком на ней выводятся необходимые символы, которые впоследствии застывают. Таблички были различной величины, толщины и качества. В зависимости от этих показателей на них записывали законы и указы, научные труды, или же рассказы простых людей, их наблюдения и случаи из жизни. История и наукаВ наши дни прослеживается четкое разделение профессий на технические, подразумевающие знание математики, физики и прочих точных наук, и гуманитарные, где главную роль играют языки, литература, история и философия. Когда существовали и развивались древние цивилизации, все эти отрасли не просто тесно переплетались между собой, но и формировали единое целое, что позволяло людям получать новые знания. Выше мы уже затрагивали такую тему, как история математики, и хотелось бы раскрыть еще пару моментов. Именно потому, что Восточному Древнему миру выпала честь быть колыбелью мировой цивилизации, он был вынужден просчитать буквально все. Достаточно рано там появилась экономика, которая строилась на таких элементах, как числовой ряд и операции с цифрами. Велись подсчеты зерна и круп, измерялись площади полей, просчитывались массы и параметры построек. Активно развивалась также астрономия. Для дальнейшего продвижения работ в этой области были разработаны первые формулы, по которым высчитывались расстояния до видимых звезд и планет. Некоторые из них ученые до сих пор используют в неизменном формате. 
Сегодня мы говорим, что математика – основа физики, химии и астрономии, но на самом деле она возникла на фундаменте данных уже существующих наук, так как была необходимостью. fb.ru Математика в Древнем Египте: знаки, цифры, примерыЗарождение математических знаний у древних египтян связано с развитием хозяйственных потребностей. Без математических навыков древнеегипетские писцы не могли бы обеспечивать проведение землемерных работ, рассчитывать количество рабочих и их содержание или производить раскладку налоговых отчислений. Так что появление математики можно приурочить к эпохе возникновения самых ранних государственных образований на территории Египта. Египетские числовые обозначения Десятичная система счета в Древнем Египте сложилась на основе использования для подсчета предметов количества пальцев на обеих руках. Числа от одного до девяти обозначались соответствующим количеством черточек, для десятков, сотен, тысяч и так далее существовали особые иероглифические знаки. Вероятнее всего, цифровые египетские символы возникли как результат созвучия того или иного числительного и названия какого-либо предмета, ведь в эпоху становления письменности знаки-пиктограммы имели строго предметное значение. Так, например, сотни обозначались иероглифом, изображающим веревку, десятки тысяч – изображением пальца. В эпоху Среднего царства (начало II тысячелетия до н. э.) появляется более упрощенная, удобная для письма на папирусе иератическая форма письменности, соответствующим образом меняется и написание цифровых знаков. Знаменитые математические папирусы написаны иератическим письмом. Иероглифика применялась в основном для настенных надписей.  Система древнеегипетской нумерации не менялась на протяжении тысяч лет. Позиционного способа записи чисел древние египтяне не знали, поскольку не подошли еще к понятию нуля не только как самостоятельной величины, но и просто как отсутствия количества в определенном разряде (этой начальной ступени достигла математика в Вавилоне). Дроби в математике Древнего Египта Египтяне имели понятие о дробях и умели производить некоторые операции с дробными числами. Египетские дроби представляют собой числа вида 1/n (так называемые аликвотные дроби), поскольку дробь представлялась египтянами как одна часть чего-либо. Исключением являются дроби 2/3 и 3/4. Неотъемлемым элементом записи дробного числа был иероглиф, переводимый обычно как «один из (некоторого количества)». Для наиболее употребительных дробей существовали особые знаки. Дробь, числитель которой отличен от единицы, египетский писец понимал буквально, как несколько частей какого-либо числа, и буквально же записывал. Например, дважды подряд 1/5, если требовалось изобразить число 2/5. Так что египетская система дробей была весьма громоздка. Интересно, что один из священных символов египтян – так называемое «око Хора» – также имеет математический смысл. Один из вариантов мифа о схватке между божеством ярости и разрушения Сетом и его племянником солнечным богом Хором гласит, что Сет выбил Хору левый глаз и разорвал или растоптал его. Боги восстановили глаз, но не полностью. Око Хора олицетворяло разные аспекты божественного порядка в мироустройстве, такие как идея плодородия или власть фараона.  Изображение ока, почитавшегося как амулет, содержит элементы, обозначающие особый ряд чисел. Это дроби, каждая из которых вдвое меньше предыдущей: 1/2, 1/4, 1/8, 1/16, 1/32 и 1/64. Символ божественного глаза, таким образом, представляет их сумму – 63/64. Некоторые историки-математики полагают, что в этом символе отражено понятие египтян о геометрической прогрессии. Составные части изображения ока Хора использовались в практических расчетах, например при измерении объема сыпучих веществ, таких как зерно. Принципы арифметических действий Метод, которым пользовались египтяне при выполнении простейших арифметических операций, состоял в подсчете итогового количества символов, обозначающих разряды чисел. Единицы складывались с единицами, десятки с десятками и так далее, после чего производилась окончательная запись результата. Если при суммировании получалось более десяти знаков в каком-либо разряде, «лишний» десяток переходил в высший разряд и записывался соответствующим иероглифом. Вычитание производилось таким же способом. Без применения таблицы умножения, которой египтяне не знали, процесс вычисления произведения двух чисел, особенно многозначных, был чрезвычайно громоздким. Как правило, египтяне пользовались методом последовательного удвоения. Один из множителей раскладывался на сумму чисел, которые мы сегодня назвали бы степенями двух. Для египтянина это означало количество последовательных удвоений второго множителя и итоговое суммирование результатов. Например, умножая 53 на 46, египетский писец разложил бы 46 на сумму 32 + 8 + 4 + 2 и составил бы табличку, которую вы можете видеть ниже. | * 1 | 53 | | * 2 | 106 | | * 4 | 212 | | * 8 | 424 | | * 16 | 848 | | * 32 | 1696 |
Суммируя результаты в отмеченных строках, он получил бы 2438 – столько же, сколько и мы сегодня, но иным способом. Интересно, что такой двоичный метод умножения применяется в наше время в вычислительной технике. Иногда, помимо удвоения, число могли умножать на десять (поскольку использовалась десятичная система) или на пять, как на половину десятки. Вот еще один пример на умножение с записью египетскими символами (косой черточкой помечались складываемые результаты).  Операция деления производилась также по принципу удвоения делителя. Искомое число при умножении на делитель должно было дать указанное в условии задачи делимое. Математические знания и навыки египтян Известно, что египтяне знали возведение в степень, а также применяли обратную операцию – извлечение квадратного корня. Кроме того, они имели представление о прогрессии и решали задачи, сводящиеся к уравнениям. Правда, уравнения как таковые не составлялись, так как еще не сложилось понимание того, что математические отношения между величинами носят универсальный характер. Задачи группировались по тематике: размежевание земель, распределение продуктов и так далее. В условиях задач присутствует неизвестная величина, которую требуется найти. Она обозначается иероглифом «множество», «куча» и является аналогом величины «икс» в современной алгебре. Условия часто излагаются в форме, которая, казалось бы, просто требует составления и решения простейшего алгебраического уравнения, например: «куча» складывается с 1/4, также содержащей «кучу», и получается 15. Но египтянин не решал уравнение x + x/4 = 15, а подбирал искомую величину, которая удовлетворяла бы условиям. Значительных успехов математика Древнего Египта достигла в решении геометрических задач, связанных с потребностями строительства и землемерных работ. О круге задач, которые стояли перед писцами, и о способах их решения мы знаем благодаря тому, что сохранилось несколько письменных памятников на папирусе, содержащих примеры вычислений. Древнеегипетский задачник Один из наиболее полных источников по истории математики в Египте – так называемый математический папирус Ринда (по имени первого владельца). Он хранится в Британском музее в виде двух частей. Небольшие фрагменты также есть в музее Нью-Йоркского исторического общества. Его также называют папирусом Ахмеса – по имени писца, переписавшего этот документ около 1650 года до н. э. Папирус представляет собой сборник задач с решениями. Всего он содержит более 80 математических примеров по арифметике и геометрии. Например, задача на равное распределение между 10 работниками 9 хлебов решалась так: 7 хлебов делятся на 3 части каждый, и работникам выдается по 2/3 хлеба, при этом в остатке имеем 1/3. Два хлеба делятся на 5 частей каждый, выдается по 1/5 на человека. Оставшуюся треть хлеба делят на 10 частей. Есть задача и на неравное распределение 10 мер зерна между 10 людьми. В результате образуется арифметическая прогрессия с разностью 1/8 меры.  Задача на геометрическую прогрессию носит шуточный характер: в 7 домах живет по 7 кошек, каждая из которых съела по 7 мышей. Каждая мышь съела 7 колосков, каждый колос приносит 7 мер хлеба. Нужно вычислить общее количество домов, кошек, мышей, колосьев и хлебных мер. Оно составляет 19607. Геометрические задачи Немалый интерес представляют математические примеры, демонстрирующие уровень знаний египтян в области геометрии. Это нахождение объема куба, площади трапеции, вычисление наклона пирамиды. Наклон выражался не в градусах, а рассчитывался как отношение половины основания пирамиды к ее высоте. Эта величина, аналогичная современному котангенсу, называлась «секед». Основными единицами длины служили локоть, составлявший 45 см («царский локоть» – 52,5 см) и хет – 100 локтей, основная единица площади – сешат, равный 100 квадратным локтям (около 0,28 Га). Египтяне успешно справлялись с вычислением площадей треугольников, применяя способ, аналогичный современному. Вот задача из папируса Ринда: чему равна площадь треугольника, имеющего высоту 10 хет (1000 локтей) и основание 4 хета? В качестве решения предлагается десять умножить на половину от четырех. Мы видим, что метод решения абсолютно верный, подается в конкретном численном виде, а не в формализованном – умножить высоту на половину основания. Весьма интересна задача на вычисление площади круга. Согласно приведенному решению, она равна величине 8/9 диаметра, возведенной в квадрат. Если теперь из полученной площади вычислить число «пи» (как отношение учетверенной площади к квадрату диаметра), то оно составит около 3,16, то есть довольно близко к истинной величине «пи». Таким образом, египетский способ решения площади круга был достаточно точным. Московский папирус Еще один важный источник наших знаний об уровне математики у древних египтян – Московский математический папирус (он же папирус Голенищева), хранящийся в Музее изобразительных искусств им. А. С. Пушкина. Это тоже задачник с решениями. Он не так обширен, содержит 25 задач, но имеет более древний возраст – примерно на 200 лет старше папируса Ринда. Большинство примеров в папирусе – геометрические, в том числе задача на вычисление площади корзины (то есть криволинейной поверхности).  В одной из задач приведен способ нахождения объема усеченной пирамиды, совершенно аналогичный современной формуле. Но поскольку все решения в египетских задачниках имеют «рецептурный» характер и приводятся без промежуточных логических этапов, без всякого объяснения, остается неизвестным, каким образом египтяне нашли эту формулу. Астрономия, математика и календарь Древнеегипетская математика связана и с календарными вычислениями, основанными на повторяемости некоторых астрономических явлений. Прежде всего, это предсказание ежегодного подъема Нила. Египетские жрецы заметили, что начало разлива реки на широте Мемфиса обычно совпадает с днем, когда на юге перед восходом Солнца становится виден Сириус (большую часть года эта звезда на данной широте не наблюдается). Первоначально простейший сельскохозяйственный календарь не был привязан к астрономическим событиям и основывался на простом наблюдении сезонных изменений. Затем он получил точную привязку к восходу Сириуса, а вместе с ней появилась возможность уточнения и дальнейшего усложнения. Без математических навыков жрецы не могли бы уточнять календарь (впрочем, окончательно устранить недостатки календаря египтянам так и не удалось).  Не менее важным было умение выбрать благоприятные моменты для проведения тех или иных религиозных празднеств, также приуроченных к различным астрономическим феноменам. Так что развитие математики и астрономии в Древнем Египте, безусловно, связано с ведением календарных расчетов. Кроме того, математические знания требуются для хронометрии при наблюдении звездного неба. Известно, что такими наблюдениями занималась особая группа жрецов – «распорядители часов». Неотъемлемая часть ранней истории науки При рассмотрении особенностей и уровня развития математики в Древнем Египте видна существенная незрелость, так и не преодоленная за три тысячи лет существования древнеегипетской цивилизации. До нас не дошли сколько-нибудь информативные источники эпохи становления математики, и мы не знаем, как оно происходило. Но ясно, что после некоторого развития уровень знаний и навыков застыл в «рецептурной», предметной форме без признаков прогресса на многие сотни лет.  По-видимому, устойчивый и однообразный круг вопросов, решаемых при помощи уже сложившихся методов, не создавал «спроса» на новые идеи в математике, которая и так справлялась с решением задач строительства, сельского хозяйства, налогообложения и распределения, примитивной торговли и обслуживания календаря и ранней астрономии. Кроме того, архаическое мышление не требует формирования строгой логической, доказательной базы – оно следует рецептуре как ритуалу, и это также сказалось на застойном характере древнеегипетской математики. Вместе с тем необходимо заметить, что научное знание вообще и математика в частности делали еще первые шаги, а они всегда самые трудные. В примерах, которые демонстрируют нам папирусы с задачами, уже видны начальные ступени обобщения знаний – пока без попыток формализации. Можно сказать, что математика Древнего Египта в том виде, как мы ее знаем (из-за недостаточности источниковой базы по позднему периоду древнеегипетской истории) – это еще не наука в современном понимании, но самое начало пути к ней. fb.ru Цифры с древности до наших времен Транскрипт 1 Краевой конкурс учебно-исследовательских и проектных работ учащихся «Прикладные вопросы математики» Алгебра Цифры с древности до наших времен Долгунов Виталий, МОУ «Лицей 10» г. Пермь, 6 кл. Кузнецова Светлана Валерьевна, учитель математики МОУ «Лицей 10» 2 СОДЕРЖАНИЕ ВВЕДЕНИЕ...3 ГЛАВА 1. Что такое число?...4 ГЛАВА 2. Цифры древних цивилизаций...5 Цифры в Древнем Египте...5 Цифры племени майя...5 Цифры Древней Греции...6 Цифры Древнего Китая...7 Славянская кириллическая нумерация...8 Римская нумерация...8 ГЛАВА 3. История возникновения арабских цифр...10 Индийская нумерация Вклад мусульман в развитие нашей системы счисления...11 Современная система счисления...11 Какая у нас система исчисления...12 Сравнение записи цифр у разных народов ГЛАВА III Организация и проведение исследования...15 ЗАКЛЮЧЕНИЕ...18 ЛИТЕРАТУРА...19 3 ВВЕДЕНИЕ «Всё есть число»- говорили пифагорейцы. Я абсолютно с ними согласен. И раньше и сейчас человека окружают числа: стоимость покупки, номер телефона, дата рождения, отметки в школе и т.п. Числа составляются из цифр. Как возникли цифры, каковы были варианты написания цифр у разных народов, что общего в их написании, каковы правила составления чисел из цифр? Эти вопросы заинтересовали меня. А так как я люблю и математику, и историю, то решил посвятить свою исследовательскую работу ответам на поставленные вопросы. Цель: доказать, что числа появились в древние время; изучить историю возникновения цифр; сравнить записи цифр разных народов. Проблема: почему мы обозначаем цифры именно так (0, 2, 3, 4, 5, 6, 7, 8, 9), а не по-другому (римскими или китайскими). Задачи: - установить, где и кем были придуманы первые числа; - научиться изображать цифры теми способами, которыми пользовались наши предки. Объект: цифры разных народов. Гипотеза: у разных народов написание цифр было похожим. Основные методы исследования: анализ литературы, сравнение, опрос учащихся, анализ и обобщение полученных в ходе исследования данных. 4 ГЛАВА 1. Что такое число? Числа были всегда и 4 и 5 тысяч лет тому назад, только правила изображения их были другими. Но смысл был один: числа изображались с помощью определённых знаков цифр. Цифра - это символ, участвующий в записи числа. Число - это величина, которая складывается из цифр по определённым правилам. Эти правила называются системами счисления 1. Никто не знает, как появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловить рыбу, научился делать каменный топор и нож. И ему приходилось считать различные предметы. Постепенно возникла необходимость отвечать на жизненно важные вопросы: по сколько плодов достанется каждому, чтобы хватило всем; сколько расходовать сегодня, чтобы оставить про запас; сколько надо сделать ножей и т.п. таким образом, сам не замечая, человек начал считать и вычислять. На протяжении многовековой истории человечества существовало множество различных способов записи числа, некоторые дошли до наших времен, а некоторые остались в истории. Пальцы всегда при нас, поэтому первоначально человек стал считать по пальцам. Таким образом, наиболее древней и простой «счетной машиной»издавна являются пальцы рук и ног. Несколько десятков лет назад учёные-археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой 30 тысяч лет тому назад какой-то охотник нанёс 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам. Узор на кости состоял из 11 групп, по 5 зарубок в каждой. При этом первые 5 групп он отделил от остальных длинной чертой. Позднее в Сибири и других районах были найдены сделанные в ту далекую эпоху каменного века (каменные) орудия и украшения, на которых тоже были черточки и точки, сгруппированные по 3, по 5, или по 7. 1 Иллюстрированный энциклопедический словарь. Москва. Научное издательство «Большая Российская энциклопедия», 1998год 5 Цифры в Древнем Египте ГЛАВА 2. Цифры древних цивилизаций Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находились очень далеко одна от другой, их числовые системы очень похожи: использование засечек на дереве или камне для записи прошедших дней. Египетские жрецы писали на папирусе, изготовленном из стеблей определенных сортов тростника, а в Месопотамии на мягкой глине. В египетской системе цифрами являлись иероглифические символы; они обозначали числа 1, 10, 100 и т. д. до миллиона. число значение 1 черта 10 пятка 100 петля веревки описание кувшинка (или лотос) палец или жаба или личинка человек с поднятыми вверх руками Числа, не кратные 10, записывались путем повторения этих цифр. Каждая цифра могла повторяться от одного до 9 раз. Например, число 4622 обозначалось следующим образом: Фиксированного направления записи чисел не существовало: они могли записываться справа налево или слева направо и даже вертикально. Например: иероглифическая запись, и обратная запись тех же иероглифов, обозначали одно и то же число - «12». Цифры племени майя  6 Очень интересная система счета была у народа Майя, который жил в Центральной Америке там, где сейчас государство Мексика. Чванливая Европа еще считала по пальцам, когда математики древних майя ввели понятие нуля и оперировали бесконечно большими величинами. Древние майя самостоятельно пришли к использованию позиционного принципа. В отличие от нас, европейцев, им не у кого было заимствовать этот принцип, и они сами додумались до него, причем почти на целое тысячелетие (!) раньше Старого Света. Запись цифровых знаков, образующих число, майя вели вертикально, снизу вверх, как бы возводя некую этажерку из цифр. Майя считали двадцатками у них была двадцатеричная система счёта. Числа от 1 до 20 обозначались точками и чёрточками. Цифры майя: Пример: 20 + =27 7 Иногда для записи цифр от 1 до 19 также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах. Цифры Древней Греции В Древней Греции имели хождение две основных системы счисления - аттическая (или геродианова) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова "пента» (пять) (буква Г употреблялась для обозначения звука "п", а не "г"). Дойдя до десяти, они ввели еще один новый символ D, первую букву слова "дека»(десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ 7 H означал 100 (гекатон), X (хилиои), символ M (мириои или мириада). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:. Вторая принятая в Древней Греции ионическая система счисления - алфавитная - получила широкое распространение в начале Александрийской эпохи, хотя возникнуть она могла несколькими столетиями раньше, по всей видимости, уже у пифагорейцев. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим, чем случайное совпадение, но у нас нет точных данных, позволяющих утверждать это со всей определенностью. Запись алфавитными символами могла делаться в любом порядке, так как число получалось как сумма значений отдельных букв. Например, записи все эквивалентны и означают число 532. Цифры Древнего Китая Эта нумерация одна из старейших и самых прогрессивных. Возникла эта нумерация около тысяч лет тому назад в Китае Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных 8 иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде ; Такая запись числа мультипликативна, то есть в ней используется умножение: и Славянская кириллическая нумерация Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. Если посмотреть внимательно, то увидим, что после "а»идет буква "в", а не "б»как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите. Чтобы различать буквы и цифры, над числами ставился особый значок титло ( ~ ) Римская нумерация Древние римляне изобрели систему исчисление, основанную на использовании букв для отображения цифр. Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы 2. Для того чтобы прочесть римскую цифру, следует следовать пяти основным правилам: Буквы пишутся слева направо, начиная с самого большого значения. Например: XV (15), CCXLIII (243), ZCXV (2115). Буквы I. X. C и M могут повторяться до трёх раз подряд, например: III (3), XX (20), ССC (300), MCCXXX (1320). Буквы V. L. D не могут повторяться. 2 9 Цифры 6, 8, 40, 80, 800 следует писать, комбинируя буквы: VII (6), VIII (8), XL (40), LXXX (80), CD (400), DCCC (800). Например, 48 следует писать, комбинируя буквы XLVIII, 449 CDXLIX _ Горизонтальная линия над буквой увеличивает её значение в 1000 раз. Например, V означает 5000, CIII и IXDL 9550. 10 ГЛАВА 3. История возникновения арабских цифр «Мы называем изобретенные индийцами цифры 1, 2,..., 9 и нуль арабскими, так как заимствовали их у арабов, но сами арабы называли эти цифры индийскими, а арифметику, основную на десятичной системе - «индийским счетом»(хисабал Хинд). В долине Инда существовала цивилизация, одним из центров которой был город, раскопанный вблизи холмов Мохенджо Даро. Эта цивилизация, основанная первоначальным населением Индии, была разрушена арийскими племенами Русов, пришедшими с Гималаев [Арийские] жрецы принесли с собой Ведическое мировоззрение и записали священные книги брахманов «Веды» ( Знания ). Ими же была создана система записи счета. К VII V вв. до н. э. относятся первые индийские посменные математические памятники Большинство научных трактатов индийцев написаны на санскрите языке религиозных книг брахманов. Этот язык объединил многочисленные народы Индии, говорившие на различных языках» (Из интернета) Индийская нумерация. Счет целых чисел в Индии с древних [арийских] времен носила десятичный характер. Санскрит индоевропейский язык, Похожий на наш: 1 - эка, 2 дви, 3 три. Наряду с цифровой записью в Индии широко применялась словесная система обозначения чисел, этому способствовал богатый по своему словарному запасу санскритский язык, имеющий много синонимов. При этом нуль обозначался словами пустое, небо, дыра ; единица предметами, имеющимися только в единственном числе: Луна, Земля; двойка словами близнецы, глаза, ноздри, губы ; четверка словами океаны, стороны света» и т. д. Применение позиционного принципа в словесной нумерации, в котором дно и тоже слово в зависимости от места имеет разное числовое значение, а названия разрядов опускаются, зафиксировано еще в V в. Например, число 1021 записывалось словами «Луна дыра крылья Луна». Одно из названий нуля «шунья»(пустое) стало впоследствии основным. Когда в VIII в. Индийские сиддханты переводили на арабский язык, слово «шунья»перевели арабским словом «сыфр», имеющим то же значение. Слово «сыфр»при переводе арабских сочинений на латынь было оставлено без перевода в виде ciffra, откуда происходит французское и английское название нуля zero, немецкое слово ziffer и наше слово «цифра», также первоначально означавшее нуль. На основе цифр брахми выработались современные индийские цифры «деваеагари» (божественное письмо), применяющиеся в десятичной позиционной системе, от которой происходят десятичные позиционные системы арабов и европейцев. 11 Вклад мусульман в развитие нашей системы счисления. Цифры, или символы наших чисел, имеют арабское происхождение, хотя они были, заимствованы арабской культуры в Индии. Промежуток между VIII и XIII веками стал одним из самых блестящих периодов в мусульманском мире. Мусульмане имели тесные связи как с азиатской, так и европейской культурами, и они и они смогли извлечь из них всё самое выдающееся. В Индии они заимствовали систему исчисления, некоторые математические методы. Современные цифры (1, 2, 3, 4 ) не совсем точно воспроизводят индийские, поскольку арабы их слегка видоизменили, приспосабливая к своему письму, но исходя из их влияния и авторитета их культуры, современные числовые символы называют арабскими цифрами, хотя арабы лишь передали в Европу способ записи чисел, разработанный индусами. «Девять индусских знаков следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски: «сифр», можно написать какое угодно число». Арабы принесли к нам способ записи чисел, которым мы сейчас пользуемся, из Индии. Однако в самой Индии до последнего времени цифры выглядели совсем не так, как в Европе. А цифры, которыми сейчас пользуются арабы, тоже не очень похожи на европейские. Одна из ненаучных гипотез происхождения начертания современных арабских цифр. Количество углов соответствует числовому значению цифры: 0 углов нет, 1 один угол, 2 два угла и т.д. Современная система счисления. Считать или, говоря ученым языком, делать количественную оценку, люди начали с тех пор, как научились отделять себя и своих сородичей от окружающего мира. Для правильного информирования своего племени требовалось сообщить как о численности преследуемой добычи, так и о многом другом например, количестве людей в соседнем племени. Прошло очень много времени, прежде чем люди освоились с большими числами. Они шли от единицы к большим числам очень медленно. С развитием человечества отдельных знаков (единиц) стало не хватать. Земледельцу надо было подсчитать урожай, скотоводу - животных, строителю - количество бревен... Умение считать и производить операции с числами высоко ценилось. Ведя счет различных предметов, люди постепенно пришли к выводу, что удобнее считать не единицами, а группами единиц. Такой счет сохранился и до 12 нашего времени (например, счет предметов парами, тройками, пятерками) и часто применяется и поныне, например, в спорте (в соревнованиях участвуют три пары спортсменов от каждой команды) и т.д. Самые разные народы по-разному называли и обозначали знаки различного количества предметов, что отразилось не только в названиях цифр и чисел, но и в их группировании, образовывая свои собственные системы счисления, другим словом НУМЕРАЦИИ. Итак, системы счисления - это способы записи (или изображения) чисел. «Различные системы счисления, которые существовали раньше и которые используются в настоящее время, делятся на две группы: позиционные и непозиционные. Системы счисления, в которых каждой цифре соответствует величина, не зависящая от её места в записи числа, называются непозиционными. В целом все непозиционные нумерации можно разделить на два вида: иероглифические, алфавитные. Первые используют для записи чисел значки разных типов, зная которые, можно составить представление о значении числа. Вторые системы записывают число в виде букв, значения которых соответствуют их месту в алфавите той или иной народности. Наиболее совершенными являются позиционные системы счисления, то есть системы записи чисел, в которых вклад каждой цифры в величину числа зависит от её положения (позиции или порядка) в последовательности цифр, изображающей число. Это значит, что основное значение имеет не столько значение, сколько место цифры (сравните и 90090). Разумеется, все позиционные системы счисления появились в результате длительного исторического развития непозиционных систем. Какая у нас система исчисления «Наша система исчисления имеет три основных характеристики: она позиционная, аддитивная и десятичная. - Позиционная, поскольку каждая цифра имеет определенное значение согласнее месту, занимаемое в ряду, выражающем числом: 2 означает две единицы в числе 52 и двадцать единиц в числе Аддитивная, или слагаемая, поскольку значение одного числа равно сумме значений цифр, образующих его. Так, значение 52 равно сумме Десятичная, поскольку каждый раз, одна цифра смещается на одно место влево в написании числа, его значение увеличивается в десять раз. Так, число 2, имеющее значение две единицы, превращается в двадцать единиц в числе 26, поскольку перемещается на одно место влево. 13 Сравнение записи цифр у разных народов При изучении записи цифр у разных народов, я пришел к выводу, что цифры большинства из них похожи. При записи чисел во всех, кроме древнекитайской 14 системы счисления, используется аддитивный способ. В Китае мультипликативная система счисления. 15 ГЛАВА 4 Организация и проведение исследования Исследование проводилось среди учащихся 5-6 классов МАОУ «Лицей 10». Всего было опрошено 53 человека. Учащимся было предложено ответить на 6 вопросов: 1 Какие цифры вы знаете или слышали. 2 Какими цифрами пользуются в современном мире. 3 Как вы думаете, откуда пришли к нам цифры. 4 Используя таблицы и правила записи цифр и чисел у разных народов (Приложение 1) записать числа 4, 9, 27, 63, 324, Как вы думаете, почему мы пользуемся арабскими цифрами для вычислений, а не римскими или китайскими. 6 Предположите, где можно было бы использовать цифры других народов? Результаты исследования: Вопрос 1: Какие цифры вы знаете или слышали Количество человек арабские римские племени майя древнеегпетские древнекитайские старославянские 40 Вопрос 2: Какими цифрами пользуются в современном мире арабскими римскими количество человек от арабов из Индии 0 Количество человек 16 Вопрос 3: Как вы думаете, откуда пришли к нам цифры. Большинство учеников ответили, что из «арабии». Из опрошенных 14 человек ответили из Индии. 17 Вопрос 4: Используя таблицы и правила записи цифр и чисел у разных народов записать числа 4, 9, 27, 63, 324, Число Способ записи (справились) Др. Египет Др. Китай Римская с.с. Майя Др.Египет Др.Китай Римская с.с. Майя Вопрос 5: Как вы думаете, почему мы пользуемся арабскими цифрами для вычислений, а не римскими или китайскими. Большинство ответили, что другими цифрами пользоваться неудобно. Запись получается громоздкой. Вопрос 6 Предположите, где можно было бы использовать цифры других народов? Многие назвали такие варианты: римские цифры для оформления. 18 ЗАКЛЮЧЕНИЕ Изучая данный вопрос я пришел к выводу, что: Числа появились в древние времена (около 5000 лет назад). Изучив историю возникновения цифр, я узнал, что арабские цифры были заимствованы арабами в Индии. Они передали данный способ записи в Европу. Современные цифры отличаются от индийских, т.к. арабы их видоизменили, приспосабливая к своему письму. Способы записи чисел в древнеегипетской нумерации, древнегреческой, славянской кириллической и римской нумерации похожи, различны только сами знаки. Способы записи чисел у древних майя и арабов также схожи. А вот в древнем Китае использовался свой особый способ записи, который называется мультипликативным (т.е. умножение). Таким образом, моя гипотеза, что способы записи чисел у разных народов схожи частично подтвердилась. В ходе исследования я установил, что арабская запись чисел 0, 1, 2, 3,4, 5, 6, 7, 8, 9 наиболее удобна и проста, в отличие, например, от древнекитайской или римской. Я научился изображать цифры теми способами, которыми пользовались наши предки. На сегодняшний день параллельно с арабскими цифрами используются и римские (для обозначения размеров одежды, веков и др.). Работать над темой мне понравилось. В дальнейшем я хотел бы рассмотреть вопросы: почему те или иные цифры получили именно такие названия, какой магический смысл вкладывался в каждую из цифр и многое другое. 19 ЛИТЕРАТУРА Иллюстрированный энциклопедический словарь. Москва. Научное издательство «Большая Российская энциклопедия», 1998год. «Занимательная арифметика» Перельман Я.И.Москва, Триада-Литера,1994 год. «Математическая шкатулка» Ф.Ф. Нагибин. Е.С. Канин. Москва, «Просвещение», 1984 год. «Что такое? Кто такой». Москва. Педагогика, 1990 год. «Что? Зачем? Почему?». Большая книга вопросов и ответов. Перевод с испанского «Школьникам о математике и математиках». Составитель Лиман М.М Москва, Просвещение год. ««Я познаю мир». Детская энциклопедия. Москва, «Астрель», 2004 год. К. Мишиной, А. Зыковой, Москва, Эксмо, 2006 год. 20 Древний Египет число значение описание 1 черта 10 пятка 100 петля веревки кувшинка (или лотос) Племя майя Приложение Славянская кириллица палец или жаба или личинка человек с поднятыми вверх руками Древний Китай 1 6 Древняя Греция Римская нумерация docplayer.ru Как считали в разных странах с начала времён«Мел» подготовил небольшой гид по истории числа, из которого можно узнать: сколько коровьих пут в мерной веревке, откуда взялась присказка «Заруби себе на носу» и как вычислить национальность человека, просто попросив его посчитать по пальцам. Рассылка «Мела» Мы отправляем нашу интересную и очень полезную рассылку два раза в неделю: во вторник и пятницу До появления числовых обозначений — цифр и букв, с которыми мы сейчас ассоциируем число, наши ранние предки пользовались «эталонами», которые они выбирали по ассоциативному принципу. Например, все знали, что Луна на небе одна, рук (или глаз) у человека две, а пальцев на каждой руке по пять. Поэтичные отголоски такой системы можно отыскать сейчас в раннем словесном счете индусов, где единицу называли Землей, Луной, Брахмой; двойку — «близнецами», «глазами»; пятерку — «чувствами» и так далее. Позднее древние окончательно определились, что считать нужно тем, чего много и что всегда при себе, и выбрали пальцы, поэтому подавляющее большинство систем счисления основано на принципе счета по десяткам (по количеству пальцев на обеих руках). Из существующих ныне исключений из этого правила можно вспомнить французский язык, где счет ведется двадцатками: 80 — quatre-vingts (4*20), 90 — quatre-vingt-dix (4*20+10). Но и здесь двадцать — это общее количество пальцев на руках и ногах. О названии цифр После того, как возникло понятие о цифрах, их нужно было как-нибудь называть. Сходство в названиях цифр у индоевропейских народов говорит о том, что они возникли, когда в ходу был общий праиндоевропейский язык — можно полагать, что имена числительных сложились до пятого тысячелетия до н. э. Однако у разных народов этот процесс мог занимать различное количество времени. Известно, что в африканском суахили существуют собственные названия для цифр 1-5, 8 и 10, а вот 6, 7 и 9 — это уже заимствования из арабского (можно сравнить: sitt, saba, tisa на суахили и «ситт», «саб’», «тис’» — на арабском). Сильное арабское влияние на африканском континенте началось с VIII века н. э., и формирование числительных в суахили относится к этому периоду.  Цифровая запись Первыми обозначениями числовых знаков для древних людей служили зарубки на твердых поверхностях: дереве, костях животных, а также узелки на веревках (знаменитый счет майя). Древнейший способ записи цифр в виде зарубок сохранился в русской присказке «заруби себе на носу».  Позднее зарубки эволюционировали в цифру 1, которая практически во всех странах изображается как короткая палочка. В обозначении цифр применялся тот же ассоциативный принцип. Например, египетская цифра 10 изображала путы для коровы:  Десять пут (то есть 100) обозначались веревкой, которой мерили поля: 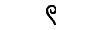 А знакомая нам римская пятерка — V — это всего-навсего изображение двух человеческих рук. Нумерация: аддитивная, субстративная и мультипликативная Арабская позиционная нумерация, которой мы пользуемся сегодня, очень проста в записи, с ее помощью удобно считать. Но не все системы счисления могли этим похвастаться. Уже упомянутая египетская система счисления была аддитивной: у единицы, десятки, сотни, тысячи (и выше) имелись свои изображения, которые при записи ставились в ряд друг за другом, а число получалось путем простого прибавления цифр. К примеру, это на самом деле является египетской записью числа 2 336: 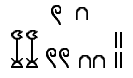 По аддитивному принципу была выстроена и греческая нумерация, заимствованная нашими древнерусскими предками, а также народами древней Грузии и Армении. Древнерусская запись числительных велась с помощью букв кириллицы или глаголицы. То есть кириллическая запись числа 217 выглядела бы как простая запись букв С I З, а на глаголице — вот так: 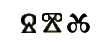 Римская нумерация — наиболее простой пример субстративного метода, смешанного с аддитивным. Здесь цифры как прибавляются друг к другу, так и вычитаются друг из друга: MXCVIII — это 1000+(100-10)+5+3=1098.  С принципами образования чисел напрямую связано то, как мы эти числа называем. В русском языке названия числительных два-дцать (2*10), пять-десят (5*10), три-ста (3*100) являются ярким примером принципа, основанного на умножении чисел. Такой принцип называется мультипликативным. А вот девя-но-сто — это результат скрещения субстративного и мультипликативного принципов. Судя по всему, изначально это число называлось «девять-десят» (в современном чешском — devadesát), а потом «перемножилось» с выражением «10 до 100». «Все есть число» В земледельческих государствах, древнейших цивилизациях Вавилон и Египет, искусство счета начало развиваться особенно быстро. Оно прежде всего было необходимо для измерения площади, пригодной для земледелия, а также для постройки зданий: храмов, дворцов. Ну, и для повседневных нужд, например, для торговли. В Древней Греции к VI–V веках до н. э. математика вошла в свой золотой период, а число для греков стало универсальным языком, на котором можно выразить законы природы. Последователи пифагорейской философско-математической школы сформулировали эту тенденцию в емкой фразе «Все есть число». С развитием международной торговли развивалось и искусство счета. Европейские купцы вплоть до XIII века активно пользовались допотопным счетом на пальцах, зародившемся еще в верхнем палеолите, а европейские ученые-математики применяли его еще несколько веков и признавали счет на пальцах великим искусством. В каждой стране была своя «техника» пальцевого счета. Даже в наши дни, если попросить континентального европейца посчитать до пяти на пальцах, он начнет поочередно разгибать пальцы руки, изначально зажатой в кулак, начиная с большого пальца. А по русской традиции счет следует вести с мизинца левой руки, загибая пальцы. Арабские цифры После крушения Римской империи наиболее влиятельной цивилизацией в средневековой Европе стала арабская. Исламские ученые VIII–XII веков вовсю переводили древнегреческие и латинские трактаты по математике, медицине, философии, физике и с помощью них далеко продвинулись в науках. В начале IX века среднеазиатский ученый Аль-Хорезми впервые выделил алгебру как самостоятельную науку («ал-горитм» — это переработанное на современный манер имя ученого, а слово «ал-джебр» впервые фигурировало в названии его сочинения). В таких условиях искусство счета совершило невероятный скачок, и в нумерации впервые возникло понятие числа «нуль» (по арабски «сыфыр» — пустой, ничто), с которым пришел и принцип позиционной системы счисления, которым мы пользуемся поныне. Эта числовая реформа совершила настоящую революцию в науке: ведь теперь вместо громоздких конструкций появились знакомые каждому школьнику лаконичные цифровые обозначения, с помощью которых очень удобно производить математические расчеты.  При этом называть современные цифры арабскими будет большой исторической несправедливостью, ведь родились они в Индии и назывались «деванагари» (божественное письмо). Индийско-арабскую систему счисления взяли на вооружение европейские ученые, когда в XII веке начали активно переводить арабских авторов на латинский язык. Распространению новой системы счета способствовало то, что начиная в XIV века в Европе стало открываться много светских школ, готовящих торговцев. С середины XV века новые цифры активно фигурировали на европейских монетах разных стран и именно тогда вошли в широкий обиход. ЧИТАЙТЕ ТАКЖЕ: 10 явлений, которые нужно убрать из школы Как управлять неуправляемым. 7 способов сделать так, чтобы подросток все-таки вас слушался «Когда я вырасту, я хочу работать тюремщиком». Необычные профессии, о которых мечтают школьники и студенты mel.fm Греческие цифры
Игры • Другие онлайн-сервисы • Главная страница
По-настоящему, греческих систем счисления известно несколько. Все они существовали в разные периоды эллинской цивилизации, следуя друг за другом. Самая древняя из известных основана на эгейских цифрах — примитивном наборе палочек и колечек из эгейского письма. Цивилизация у островных греков была основана на торговле, и для этой цели счёт очень пригодился. Однако с полной утратой письменности в результате вторжения дорийцев в XII веке до н.э. всякая вычислительная деятельность у древних греков прекратилась, и мы вообще не знаем, чем они занимались ещё пятьсот лет в состоянии угнетения и скуки, пока в VII веке до н.э. их интеллектуальный отдых внезапно не закончился в связи с кипучей деятельностью некоего Фалеса, милетского олигарха, разбогатевшего на торговле маслинами. Сообразив, что греки делили землю до этого неправильно и ненаучно, оный, подучившись на курсах в могущественном Египте, активно включился в передел земли. Так появилась наука геометрия, сиречь землемерие, и, слава Гермесу, вычисления снова понадобились. Несмотря на то что до нас не дошло ни одно из его произведений и мы не знаем, существовали ли они, новозадуманная система счисления распространилась под названием аттической, и все Пифагоры, Платоны и Аристотели не стесняясь ею пользовались. Такая система мало отличается от последующей за ней римской — разве что тем, что цифры в ней осмысленны и являются первыми буквами слов, означающих соответствующие числа. Как если бы по-русски единицу означало бы Е, пятёрку — П, десятку — Д, сотню — С, тысячу — Т, а их сочетание ТССДДДЕЕЕЕ давало бы значение 1234. Вот точно так же греки пользовались своими буквами:
| Ι | Π | Δ | ΠΔ | Η | ΠΗ | Χ | ΠΧ | Μ | ΠΜ | | 1 | 5 | 10 | 50 | 100 | 500 | 1000 | 5000 | 10000 | 50000 |
Их ещё называют геродиановыми знаками по имени историка Геродиана, несмотря на то что он жил спустя пятьсот лет после того, как эта система полностью вышла из употребления. Здесь несколько непривычные и неподдающиеся компьютерному набору полуразрядные цифры для 50, 500, 5000 и 50000 образованы путём вплетения полноразрядных в пятёрку, а 1234 равняется ΧΗΗΔΔΔΙΙΙΙ. Любой, кто знаком с римскими цифрами, легко сможет с помощью данной таблицы записать и аттические. К сожалению, в этой системе ещё не применялось правило вычитания, придуманное только в Средневековье, поэтому здесь нельзя ставить цифру меньшую перед большей с тем, чтобы вычесть её, а не сложить, как это проделывается с римским IV. Цифры должны идти строго по убыванию и не более четырёх одинаковых подряд.
Затем с греками случилось озарение, пришедшееся опять на славный город Милет, где последователи местной научной школы разработали в V веке до н.э. наконец полностью оригинальную систему счисления, которую называют милетской или, чаще, ионийской. Именно её начали использовать Евклиды, Архимеды и все последующие Эратосфены, безостановочно все византийцы, а за ними и иные народы в переработанной на свои национальные азбуки форме, включая нашу родную кириллицу, пока всё их многообразие в результате неравной борьбы не было выведено из строя более стройной арабской системой, окончательно захватившей мир. Тем не менее греческие цифры ионийской системы употребляются в некоторых случаях даже в современном греческом языке, а также в их богослужебной литературе. И данный сервис обслуживает именно эту последнюю из трёх систем, ныне действующую.
Греки снова не стали выдумывать отдельных знаков для цифр, а использовали уже существующие буквы своего алфавита. Казалось бы, для десятичной записи достаточно и десяти цифр, но грекам не хватило усилия, чтобы признать ноль числом и выдумать цифру для его обозначения. Поэтому в десятичном порядке у них может быть только девять значащих цифр, а для нуля — пропуск разряда. Зато они не поскупились задействовать всю ширину своего алфавита, коий содержал на тот момент не менее 27 букв, а значит, им можно было описать число сразу на три десятичных порядка. И буквам присвоили следующие числовые значения:
| Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ϟ | | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | Ϡ | | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Заглавные буквы, а не привычные строчные здесь потому, что, во-первых, само минускульное начертание, положенное в основание этих строчных, появилось лишь в IX–X веках н.э., и в Древней Греции никаких букв αβγδε в глаза никогда не видали. А во-вторых, всё же будучи используемыми всю византийскую историю, в современной Греции строчные буквы вернули право обозначать цифры обратно заглавным. Также должны здесь бросаться в глаза три неклассические буквы, не входящие в современный алфавит, но всё ещё использующиеся как цифры: ϠϞϚ. Случилось так потому, что греки позаимствовали свой алфавит у финикийцев, произносящих некоторые звуки, которых у греков не было, и буквы этих звуков должны были либо видоизмениться, либо со временем исчезнуть.
Стигма Ϛ — буква, имевшая недолгое употребление в византийский период и являющаяся лигатурой букв сигмы ς и тау τ. Сегодня при практической невозможности написать эту нестандартную букву она просто заменяется на ΣΤ, даже для числового обозначения. Предок славянской буквы зело Ѕ, аналогично равной 6. Что интересно, изначально её место занимала другая буква — дигамма Ϝ — предок латинской F, сохранившей-таки шестое место в алфавите. Названная «двойной гаммой» чисто за внешность, она издавала звонкий лабиовелярный аппроксимант, как потомок финикийской гламурной буквы вау. В дополнение необходимо сказать, что в греческом языке две строчных сигмы: ς — ставящаяся в конце слов и σ — во всех остальных случаях. Но в качестве цифры первая никогда не используется. Если же в числе стоит что-то похожее на неё, то это стигма ϛ: в некоторых шрифтах они выглядят полностью идентично. Не запутайтесь!
Коппа Ϟ — буква, имевшая изначальное начертание Ϙ, затем Ҁ, но чем дальше, тем больше Ϟ, и издававшая язычковый вариант звука Κ. Предок латинской Q. Дольше всех, до V века н.э., продержалась в дорийском диалекте, имевшим наибольшее воздействие финикийского.
Сампи Ͳ — буква, подозрительно похожая на тау Τ с обвислыми ушами, но издающая свистящий звук вроде Ц, во времена создания ионийской системы всё ещё бытовавший в ионийском диалекте. Затем по исчезновению звука, в длительное отсутствие живого употребления (лишь только в качестве цифры), она приобрела поистине устрашающие формы: Ϡ, или на худой конец Ϡ. Некоторые полагают, что именно от неё произошли славянские буквы Ѫ и Ѧ, несмотря на то что они вообще-то гласные. Тем не менее в славянской системе счисления буква Ѧ изначально имела то же числовое значение 900, что и сампи. Однако в конце XIV века произошло вторичное чудо: внезапно и как бы случайно значение 900 учёные мужи у Ѧ отобрали и отдали не какой-нибудь, а именно букве Ц! Как знали, что так звучала сампи две тысячи лет назад у давно вымершей расы!
Итак, тремя десятичными цифрами можно досчитать до тысячи, но греки уже привыкли считать до десяти тысяч, и для ещё одного разряда они придумали помечать цифру тысяч знаком «͵» (от которого произошёл славянский знак тысяч «҂»). Хотя по непонятной причине установка такого знака перед цифрами от Ι до Ϡ для обозначения десятков и сотен тысяч осталась неправомерной. Вместо этого для записи цифры десятков тысяч, называемых у греков мириадами, они начали прибавлять к значащей цифре букву Μ, а затем приноровились писать полное число мириад над нею. Таким образом число разрядов удалось удвоить до восьми: 12345678 = Μ͵ασμγ͵εχοη. Позже число мириад могли написать с двоеточиями: ͵α̈σ̈μ̈γ̈͵εχοη. Но затем Диофант придумал наконец просто отделять мириады точкой: ͵ασμγ . ͵εχοη — и за одно как решать кубические уравнения вида: ΚΥ η̅ Λ|ΔΥ ι̅ϝ̅ ἴσ ΚΥ α̅. А Архимед, живший в то же время, решил как-то посчитать число песчинок, которые поместятся внутри Вселенной, и был вынужден для этой цели активизировать до 20 квадриллионов таких мириад. Да, наука била ключом!
Для выделения числа в тексте в Средневековье служило надчёркивание горизонтальной чертой над всем числом. В сущности, этого же происхождения и славянское титло. В современном греческом языке для этой цели служит кавычка «ʹ», ставящаяся в конце числа. Например, число 1111 превращается в слово ͵αριαʹ. Вышеописанными числами нумеруются главы книг, ими ведётся нумерация царей и пап: например, ещё пару лет назад католическим миром правил Βενεδικτος ΙΣΤʹ, пока не отрёкся, а Αλεξανδρος Γʹ, император Третьего Рима (Ρώμη Γʹ), был отцом следующего за ним Νικολαος Βʹ. Кроме того, ещё в начале прошлого века так в Греции нумеровали законы: например, до сих пор действует закон ͵ΓϠΝʹ «Об уголовной и гражданской ответственности водителей автотранспортных средств».
  www.konorama.ru Греческие цифры и их взаимосвязь с буквамиВсе мы пользуемся цифрами: считаем пролетевшие годы, денежные знаки, количество цветов в букете юбиляра и тарелок на праздничном столе. Без них жизнь не представляется возможной. Умение считать прививается нам с детского сада, а то и раньше. 
Малыши учатся вести счёт на палочках, затем - на простых примерах, далее в ход идёт таблица умножения. Взрослые с лёгкостью конвертируют валюты, меры длины и величины, подсчитывая семейный бюджет, вложения в бизнес или сотки на приусадебном участке. К слову, цифры и числа - это взаимосвязанные, но разные категории. Цифра несёт в себе обозначение числа, которое, в свою очередь, отображает его количественную референцию (или характеристику) и представляет собой совокупность цифр. 
История цифр и чиселА знаете ли вы, как появились цифры? За такими привычными нам с детства значками кроется целая история, пропитанная духом древности и веяниями старины. Если проследить историю появления цифр, можно лицезреть традиции и культуру многих народов, живших задолго до нас. Наши давние предки вместо цифр оставляли зарубки в виде прямых насечек и закорючек на прочной древесине, костях и камнях для обозначение количества запасённой пищи, примитивного оружия и тому подобного. Одна зарубка - одна единица, тысяча зарубок - тысяча единиц. Правда, наши пращуры знали всего несколько исчислений - "один", "два" и "много". В своих изысканиях учёные мужи периодически попадают в замешательство, поскольку история возникновения цифр и чисел чрезвычайно запутана. Достоверно известно, что самые первые письменные цифры появились в Месопотамии и Древнем Египте. При этом в Месопотамии пользовались клинописью, а в Древнем Египте - скорописными иероглифами. Месопотамцы наносили значки на специальные глиняные таблички, а египтяне использовали для этих целей папирусы. Именно у египтян цифры позаимствовали древние греки, переделав их на свой лад. 
Учение из ГрецииЧто же собой представляли греческие цифры? В Древней Греции было две системы цифр и чисел - аттическая и ионическая. Видимо, это связано с умственным трудом математиков и философов, проживающих на земле мифов и легенд и соревнующихся друг с другом в математических изысканиях. Аттическая система схожа с десятичной, однако главенствует в ней цифра 5. Греческие цифры, представленные аттическим исчислением, представляли собой повторение коллективных знаков и были схоже с месопотамским. Цифра 1 обозначалась как чёрточка, 2 - две чёрточки, 3 - три чёрточки, 4 - соответственно 4 чёрточки. Цифра 5 обозначалось первой буквой греческого слова "пэнта", а 10 - первой буквой слова "дэка". Перед там как в Греции наступила Александрийская эпоха, появилась ионическая система исчисления - греческие цифры, которые представляли собой тандем десятеричной системы чисел и вавилонского метода. Цифры представляли собой рисунок из чёрточек и букв, однако были довольно сложными для использования простыми людьми. Такой системой пользовался великий Архимед и другие известные личности того времени. 
Союз букв и чиселНа данный момент в некоторых случаях используется ионическая нумерация - с её помощью можно записать числа только от 1 до 99.999.999, используя греческий алфавит и зная, какая буква несёт в себе числовое значение единиц, десятков и сотен. К слову, такие числа легко читаются обычными словами. Именно греки стали первопроходцами, от которых этот метод исчисления переняли арабы, семиты и славяне. Древнегреческий алфавит состоял из 24 букв, к ним добавили ещё 3 буквы, которые не использовались несколько тысяч лет. В итоге получили 27 букв, которые впоследствии поделили на 3 группы, каждая включала в себя по 9 букв. В первую группу входили цифры от 1 до 9, при этом цифра 1 обозначалась первой буквой алфавита "альфа", 2 - второй буквой "бета", и так далее до цифры 9, обозначающейся буквой "тета". Вторая группа включала в себя греческие цифры от 10 до 90, а третья - от 100 до 900. Числа от 1000 и больше обозначали следующим образом: первой писали соответствующую букву из первой группы (единичного разряда), затем ставили запятую и писали буквы из первой и второй группы. Самое большое число - 10.000 - называлось отдельно и обозначалось буквой "М". Спустя некоторое время букву заменили просто точкой. На данный момент времени греческая азбука включает в себя всего двадцать букв. Вам нужно использовать, а тем более проговаривать греческие цифры? Произношение имеет немаловажное значение. Для этого нужно хотя бы немного знать алфавит. Освоить его поможет эта статья. Для удобства мы сделали две таблицы, в которых приведены не только буквы, но и греческие цифры, перевод их на русский язык и транскрипция (произношение). Знакомство с греческим алфавитом| Прописные и строчные буквы | Греческое название латинскими буквами | Транскрипция | Перевод греческой буквы на русский язык | | Α, α | Alpha | [′ælfə] | альфа | | Β, β | Beta | [′bi:tə] | бета | | Γ, γ | Gamma | [′gæmə] | гамма | | Δ, δ | Delta | [′deltə] | дельта | | Ε, ε | Epsilon | [′epsəֽlɔn] | эпсилон | | Ζ, ζ | Zeta | [′zeitə] | зета | | Η, η | Eta | [′eitə] | эта | | Θ, θ | Theta | [′theitə] | тхета | | Ι, ι | Iota | [ai′outə] | йота | | Κ, κ | Kappa | [′kæpə] | каппа | | Μ, μ | Mu | [mju:] | мю | | Ν, ν | Nu | [nju:] | ню | | Ξ, ξ | Xi | [ksi:] | кси | | Ο, ο | Omicron | [′ɔməֽkrɔn] | омикрон | | Π, п | Pi | [pai] | пи | | Ρ, ρ | Rho | [rou] | ро | | Σ, ς | Sigma | [′sigmə] | сигма | | Τ, τ | Tau | tɔ:] | тау | | Υ, υ | Upsilon | [′ju:psəֽlɔn] | ипсилон | | Φ, φ | Phi | [fi:] | фи | | Χ, χ | Chi | [kai] | хи | | Ψ, ψ | Psi | [psi:] | пси | | Ω, ω | Omega | [′oumegə] | омега |
Считаем до двадцати по-гречески| Цифры | Написание на греческом языке | Произношение на русском языке | | 1 | ένας | эна | | 2 | ένας | зио | | 3 | τρια | триа | | 4 | τεσσερα | тэссера | | 5 | πεντε | пэндэ | | 6 | εξτ | экси | | 7 | εφτα | эфта | | 8 | οχτω | окто | | 9 | εννια | эннья | | 10 | δεκα | дэка | | 11 | εντεκα | энзэка | | 12 | δωδεκα | додэка | | 13 | δεκατρεις | дэкатрис | | 14 | δεκατεσσερις | дэкатесеррес | | 15 | δεκαπεντε | дэкапэндэ | | 16 | δεκαξτ | дэкаэкси | | 17 | δεκαεφτα | дэкаэфта | | 18 | δεκαοχτω | дэкаохто | | 19 | δεκαεννια | дэкаэннья | | 20 | εικοστ | икооси |
Пользователям Word на заметкуЧто посоветовать активным пользователям Microsoft Office, которые хотят попробовать перевести греческие цифры в Word? Первым делом нужно установить сам "Ворд", а затем MS Office Proofing Tools SP1. Это необходимо для полноценного использования MS Office Word. Также необходимо настроить греческую раскладку клавиатуры. Как это сделать? Подведите курсор мышки к индикатору клавиатуры, расположенному в нижнем правом углу монитора, и кликните по нему правой кнопкой. Далее в появившемся меню выберите следующие пункты: "Настройки" --> "Язык" --> "Раскладка клавиатуры" --> "Greek" --> "Greek Polytonic". Если вы достаточно хорошо знаете стандартную английскую раскладку, в дальнейшем пользование греческой не составит труда. fb.ru История цифр для детей (с видео) Все мы знаем, что используем при счете арабские цифры. Однако как они появились и дошли до нас? Процесс возникновения арабских чисел очень интересен и занимателен.  Как впервые возникли цифры и числа? Как впервые возникли цифры и числа?Как они зародились? Десятичная система арабского счета включает в себя 10 основных чисел от 0 до 9. С их помощью можно записать цифру любой величины. До происхождения цифр люди пользовались пальцами для счета, но однажды им понадобилось посчитать такое большое количество предметов, что пальцев уже не хватало. Так возникла запись чисел. История цифр началась 5 тысячелетий назад в Египте и Месопотамии. И хотя эти два культурных пласта мало пересекались друг с другом, их системы исчисления очень похожи. Первоначально для записей использовали камень или выполняли засечки на дереве. Впоследствии в Месопотамии стали пользоваться глиняными табличками, а в Египте писали на папирусе. Внешний вид цифр в этих культурах отличается, однако одно можно сказать точно: найденные археологами артефакты подтверждают, что это были не просто записи чисел, а именно математические действия.  Основные методы исчисления в древности. Основные методы исчисления в древности.История происхождения арабских цифр в том виде, в каком мы их знаем сегодня, довольно запутана. Точное время их возникновения неизвестно, однако ученые знают наверняка, что впервые числами стали пользоваться астрономы. Между 2 и 6 веками н.э. астрономы Индии узнали о греческой шестидесятеричной системе исчисления и переняли у греков ноль. Затем основы греческого исчисления были совмещены в Индии с десятичной системой, заимствованной из Китая. Именно в Индии стали обозначать цифры одним символом. Популяризатором индийской записи стал ученый по имени Аль-Хорезми, который написал труд под названием «Об индийском счете». Впоследствии книга об исчислении была переведена на латинский язык, что привело к распространению десятичной системы в Европе. Именно Индии мы сегодня обязаны возникновению арабских чисел, что произошло около 5 века н. э. Уже в 10-12 веках арабские цифры стали известны Европе. Это произошло благодаря захвату Испании маврами, принесшими с собой мусульманскую культуру и арабские книги. Ученый по имени Сильвестр, прибывая в мусульманской Кордове, мог получить доступ к такой литературе, которую Европа еще не знала. Поскольку часть Испании по-прежнему оставалась христианской, перевод индийской книги на латынь позволил популяризировать ее в христианской Европе. На Руси почти до времен Петра для обозначения чисел использовали старославянские буквы. С приходом европейской культуры стала внедряться арабская система записи. Поскольку старославянская азбука с древних времен существенно изменилась, арабские цифры глубоко вошли в нашу жизнь. Арабские цифры были намного удобнее римских и быстро завоевали популярность. Сегодня мы пользуемся ими во всех областях нашей деятельности. Присмотритесь внимательно: мы используем числами, чтобы просматривать телевизионные передачи, разговаривать по телефону, получать деньги с банковского счета, измерять время, покупать продукты и многое другое. Без чисел наша современная жизнь просто невозможна. Так почему же цифры, придуманные в Индии, стали называть арабскими? В 7 веке нашей эры образовалось новое государство – Арабский халифат, который захватил в свое господство северо-запад Индии. Арабы насаждали на этих землях свою культуру, но в результате именно достижения индийских астрономов дали миру десятичное исчисление, а арабский ученый Аль-Хорезми только популяризировал ее. Так что получилось, что европейцы знали о цифрах уже от арабов. История чисел (слайды презентации)  
   
Как они выглядят? У детей часто возникает вопрос: почему цифры выглядят именно так, какими мы их знаем? Какова история появления цифр именно в таком виде, как мы знаем их сейчас? Письмо на бумаге существенно изменило первоначальный облик арабских цифр. Поскольку древние люди вынуждены были писать числа на глине, дереве или папирусе, движения руки были затруднены. Легче было рисовать не скругленные формы, а линии и углы. Именно поэтому первоначальные цифры составлялись из черт. Их комбинации не случайны: каждая цифра содержала столько углов в написании, сколько обозначало само число. Например, в единице мы видим один угол, в двойке – два угла и т. д. Частично восстановить древнее начертание арабских цифр помогут электронные часы, где обозначения существенно отличаются от прописных и тоже состоят из линий и углов. Видео-материал по теме Итак, история цифр очень интересна и насчитывает сотни лет. Обойти стороной эту информацию в детских садах и начальных классах школы просто невозможно. История появления арабских чисел может стать плодотворной почвой для организации тематического утренника или КВН. Подготовьте викторину, попросите детей самим подобрать интересную информацию об истории чисел. Они наверняка с увлечением отнесутся к подготовке и участию в мероприятии.  Загрузка... Загрузка... steshka.ru
|
