Математика в Древнем Египте — Википедия. Числа в древнем египте
Способы счета и измерения времени у древних народов
Греки вообще считали, что наука появилась в Египте. Аристотель, например, пишет:
«По этой причине возникла в Египте наука; именно там жрецы имели необходимое свободное время».
Геродот, который лучше знал Египет, смотрел больше на практическую сторону дела: когда Нил заливал участок
обработанной земли, то с точки зрения обложения нужно было установить, сколько земли было потеряно, -
«и это было, как мне кажется, начало геометрии, которая оттуда перешла в Грецию (Геродот)»
Самым большим и наиболее известным из египетских математических текстов
является папирус Ринда. Этот источник относится к периоду Среднего Царства,
времени расцвета древнеегипетской культуры, ок. 1650г. до н.э. Папирус
начинается очень широковещательно: он обещает научить «Совершенному и
основательному исследованию всех вещей, пониманию их сущности, познанию
всех тайн…». На деле в папирусе находились лишь тайны счета и искусства
вычислений с дробями, в которые должен быть посвящен читатель на примере
различных практических задач. Например, распределение заработной платы между
известным числом рабочих, вычисление необходимого количество зерна для
приготовления такого-то количества хлеба или пива, вычисление поверхностей
и объемов, перевод одних мер зерна в другие. Среди них находятся, однако,
и чисто теоретические задачи для упражнения в трудном искусстве вычислений с
дробями. Такого рода вычисления были нужны сословию царских писцов. Папирус
был предназначен для преподавания в школе писцов.
Древнеегипетская нумерация была похожа на римскую: поначалу были
отдельные значки для 1, 10, 100, … 10 000 000, сочетавшиеся аддитивно
(складываясь). Египтяне писали справа налево, и младшие разряды числа
записывались первыми, таким образом, в конечном счёте порядок цифр
соответствовал нашему. В иератическом письме уже есть отдельные обозначения
для цифр 1-9 и сокращённые значки для разных десятков, сотен и тысяч.
Любое число в Древнем Египте можно было записать двумя способами: словами
и цифрами.
Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число.
Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу
значений:
1 x 2 = 2
2 x 2 = 4
4 x 2 = 8
8 x 2 = 16
16 x 2 = 32
Пример разложения числа 25:
Кратный множитель для числа «25» — это 16.
25 — 16 = 9,
Кратный множитель для числа «9» — это 8,
9 — 8 = 1,
Кратный множитель для числа «1» — это 1,
1 — 1 = 0
Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1.
Пример: умножим «13» на «238»:
Список литературы
ulm.udsu.ru
В ДРЕВНЕМ ЕГИПТЕ ЧИСЛА ПЕРВОГО ДЕСЯТКА, Обозначения натуральных чисел
Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами. В Древнем Египте числа первого десятка записывали соответствующим количеством палочек. Числа и бизнес пребывают в прочном тандеме. Гораздо лучше придумали запись чисел в древнем Вавилоне.
Нам ничего не известно о развитии математических знаний в Египте как в более древние, так и в более поздние времена. Дошедшие до нас экземпляры — это в основном копии, переписанные в период гиксосов. Носители научных знаний тогда именовались писцами и фактически были государственными или храмовыми чиновниками.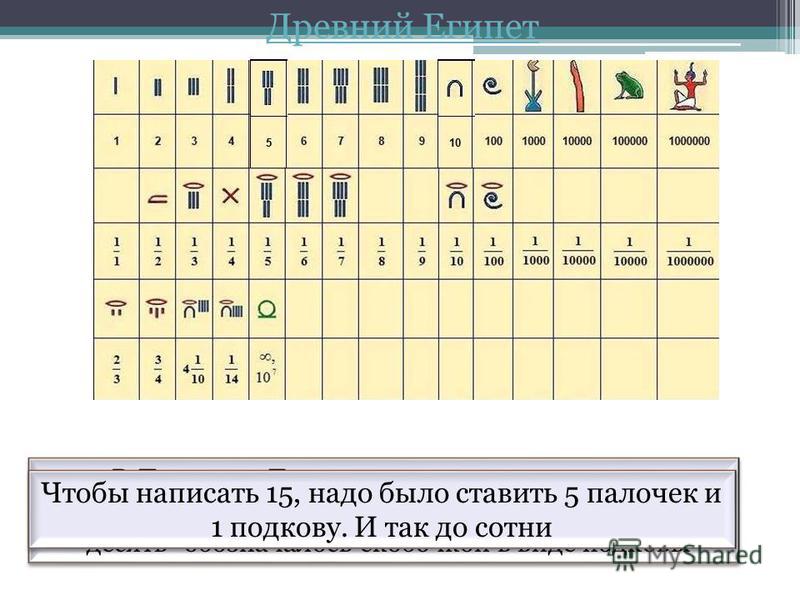
Тем не менее, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет имела или, по крайней мере, начинала приобретать теоретический характер. Древнеегипетская нумерация, то есть запись чисел, была похожа на римскую: поначалу были отдельные значки для 1, 10, 100, … 10 000 000, сочетавшиеся аддитивно (складываясь).
Деление заключалось в подборе делителя, то есть как действие, обратное умножению. Особые значки обозначали дроби вида 1n{\displaystyle {\frac {1}{n}}} и 23{\displaystyle {\frac {2}{3}}}. Однако общего понятия дроби mn{\displaystyle {\frac {m}{n}}} у них не было, и все неканонические дроби представлялись как сумма аликвотных дробей. Типовые разложения были сведены в громоздкие таблицы. Действительно, греческие учёные сообщали, что в Египте для построения прямого угла использовалась верёвка, разделённая на 12 частей.
В любом случае, нет никаких свидетельств, что в Древнем Египте была известна теорема Пифагора в общем случае (в отличие от Древнего Вавилона). Вам, наверное, кажется, что правила записи чисел и правила вычислений с ними всегда были такими же, как сейчас. На самом деле, люди сначала очень долго учились называть числа, потом их стали изображать на коре деревьев, на костях животных, на камне…
Одевались в шкуры убитых зверей. Их учителем была сама жизнь. Поэтому и «обучение шло медленно. Поначалу они определяли это соотношение как «один» и «много». Для этого он должен был уметь считать, а так как названий чисел тогда еще не было, он показывал число на пальцах.
Так, в Китае и Японии предметы домашнего обихода (чашки, тарелки и др.) считают не дюжинами и полудюжинами, а пятерками и десятками. Во Франции и в Англии и поныне в ходу счет двадцатками. Названия чисел — у многих народов указывают на ; их происхождение. А в другом племени считали так: 1 — мал, 2 — булан, 3 — гулиба, 4 — булан-булан, 5 — булан-гулиба, 6 — гулиба-гулиба.
Вот как трудно было людям научиться считать! В разных странах и в разные времена это делалось по-разному. Когда люди не умели еще делать бумагу, записи появлялись в виде зарубок на палках и костях животных, в виде отложенных ракушек или камешков или в виде узелков, завязанных на ремне или веревке. Вглядись внимательно в рисунок. И это не шутка. Рисовали такого человечка древние египтяне, когда хотели изобразить миллион.
А «десять» обозначалось скобочкой в виде подковы. Чтобы написать 15, надо было ставить 5 палочек и 1 подкову. И так до сотни. Для сотни придуман был крючок, для тысячи — значок вроде цветка. Не очень-то удобно было записывать таким способом большие числа и совсем неудобно было их складывать, вычитать, умножать, делить. Очень большая возня была с этими значками-иероглифами!
Очень разные и порою даже забавные были эти «цифры» у разных народов. Посмотрите, как обозначали числа древние греки и славяне. Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему.
Популярное сегодня:
Посмотрим, посмотрим:
ytrubaser.ru
Обозначение чисел и счет в Древнем Египте
Обозначение чисел и счет в Древнем Египте.
Примерно в третьем тысячелетии до нашей эры египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и так далее использовались специальные знаки. Вот они:
Все остальные числа составлялись из этих символов при помощи сложения.
Н-р: чтобы записать число 3252, рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы):
Величина числа не зависела от того как располагались его знаки: их можно было записывать сверху вниз, справа налево или вперемешку.
Система счисления называется непозиционной, если в ней количественные значения символов, используемых при записи чисел, не зависят от места их положения в коде числа.
Система счисления Древнего Египта является непозиционной.
Римская система счисления
Система счисления называется непозиционной, если в ней количественные значения символов, используемых при записи чисел, не зависят от места их положения в коде числа.
Примером непозиционной системы счисления, которая сохранилась до наших дней, может служить система счисления, применявшаяся более двух с половиной тысяч лет назад в Древнем Риме.
В основе римской системы счисления лежат знаки I (один палец) для числа 1, V(раскрытая ладонь) для числа 5, Х (две сложенные ладони для числа 10, а также специальные знаки для обозначения чисел 50,100,500 и 1000.
Римскими числами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать).
Римская система счисления сегодня используется в основном для наименования знаменательных дат, томов, разделов и глав в книгах.
Вавилонская система счисления
Идея приписывать цифрам разные величины в зависимости от того, какую позицию они занимают в записи числа, впервые появилась в Древнем Вавилоне примерно в третьем тысячелетии до нашей эры.
До нашего времени дошли многие глиняные таблички Древнего Вавилона, на которых решены сложнейшие задачи. Для записи чисел вавилоняне использовали всего два знака: клин вертикальный (единицы) и клин горизонтальный (десятки). Все числа от 1 до 59 записывались с помощью этих знаков.
Был у вавилонян и знак, игравший роль нуля.
Все число в целом записывалось в позиционной системе счисления с основанием 60. Отголоски этой системы счисления мы находим в сохранившемся до наших дней обыкновении делить один час на 60 минут, одну минуту на 60 секунд.
Ясачные грамоты
В старину на Руси среди простого народа широко применялись системы счисления, отдаленно напоминающие римскую. С их помощью сборщики податей заполняли квитанции об уплате подати – ясака (ясачные грамоты) и делали записи в податной книге.
Употребляемые в квитанции знаки означают:
А чтобы нельзя было сделать никаких прибавлений, все знаки а
А чтобы нельзя было сделать никаких прибавлений, все знаки очерчивались по контуру прямыми линиями. Н-р: 1232 рубля 24 копейки.
Десятичная система счисления
Обычная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой мы производим все наши вычисления, - пример позиционной системы счисления.
В привычной нам системе счисления для записи чисел используются десять различных знаков (цифры 0,1,2,3,4,5,6,7,8,9) поэтому ее называют десятичной. Цифры в записи числа имеют определенное значение. Поэтому данную систему счисления называют позиционной. Н-р: в числе 255 цифры 5 имеют различные количественные значения – 5 десятков и 5 единиц.
Потребовалось много тысячелетий, чтобы люди научились называть и записывать числа так, как это делаем мы с вами. Начало этому было положено в Древнем Египте и Вавилоне. Дело в основном завершили индийские математики в 5-7 веках нашей эры. Важным достижением индийской науки было введение особого обозначения для пропуска разрядов – нуля. Арабы, познакомившись с этой нумерацией первыми, по достоинству ее оценили, усвоили и перенесли в Европу. Получив название арабской, эта система в 12 веке нашей эры распространилась по всей Европе. И так как эта система счисления проще и удобнее остальных, быстро их вытеснила. Сегодня десятичными цифрами выражаются время, номера домов и телефонов, цены и т.д.
Время многократно изменяло облик десятичных цифр, пока они не приобрели привычный для нас вид.
Такое изображение десятичных цифр не случайно, каждая цифра обозначает число, соответствующее количеству углов в ней. Подсчитайте и убедитесь в этом сами!
Изучая эту систему счисления с раннего возраста и используя в повседневной практике, многие люди не догадываются о существовании других систем счисления.
Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами. В Древнем Египте числа первого десятка записывали соответствующим количеством палочек. Числа и бизнес пребывают в прочном тандеме. Гораздо лучше придумали запись чисел в древнем Вавилоне. 
