Старинные русские задачи по математике. Древняя задача по математике
Старинные задачи и способы их решения

 Введение Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.
 Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
 Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением. Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач. Задачи исследования: - исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
- исследовать старинный способ решения задач на сплавы и смеси.
 Диофант Его называют отцом алгебры Диофант умел решать очень сложные уравнения, он применял для этого буквенные обозначения и другие приемы. Биографические данные зашифрованы в виде математической задачи, начертанной на его гробнице .
 Задача № 1 Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись: «Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»





 Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого. После определения числового выражения - переход на следующий слайд (верхняя кнопка) Попадая повторно на этот слайд повторяем определение буквенных выражений. Далее: Чтобы получить второе определение – нажмите на «Знайку». После определения буквенных выражений нажмите на вторую кнопу и Вы перейдете к практическому заданию.
 Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739) Магницкий Л.Ф. (при рождении Телятин)- русский математик, педагог; преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике (в 1703г. «Арифметика»), которая более ста лет являлась основным учебным пособием по математике в России.
 40-30 30-5 Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять? Параметры конечного продукта Параметры исходных продуктов Доли исходных продуктов в конечном продукте 5% 1-ый продукт 10 частей 30% 25 частей 40% 2-ой продукт Соотношение первого и второго растворов – 10:25 или 2:5.
 Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора? Решение: 2 + 5 = 7(ч) - Сколько грамм приходится на одну часть?
140 : 7 = 20(г) - Сколько грамм 5%-го раствора взять?
2 · 20 = 40(г) - Сколько грамм 40%-го раствора взять?
5 · 20 = 100(г) Ответ: для получения 140г 30%-ного раствора нужно взять 5%-ного раствора 40г, а 40%-ного - 100 г.
 Заключение Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой. Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор. «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич) .
 Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы. В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу. videouroki.net Презентация "Старинные задачи" - Математика
Просмотр содержимого документа
«Презентация "Старинные задачи"»
 Старинные задачи Жилин Павел 5б
 - В старинные времена нашим предкам было
необходимо считать , сравнивать. Узнавать , кто больше принес домой добычи и сколько дать еды каждому человеку в семье. Знать, каких и сколько ресурсов для изготовки еды, посуды и многого другого. И для придумали считать , а затем решать задачи для нахождения какой-либо информации. Сохранились , к счастью некоторые задачи.
 Задача Древнего Египта - В доме живут семь людей , у каждого человека по семь кошек , каждая кошка в день съедает семь мышей, каждая мышь съедает по семь колосков, в каждом колоске вырастает по семь зернышек. Как велики числа в задаче и их сумма.
Ответ:всего 7 людей, 49 кошек,343 мышки, 2401 колосок, 16807 зернышек. Сумма – 19607.
 Задача Пифагора - Правитель острова Самос Поликрат спросил у Пифагора , сколько у него учеников. « Охотно
скажу тебе, Поликрат – сказал Пифагор – половина учеников изучают математику , четверть исследуют тайны вечной природы, седьмая часть молча упражняют силу духа , храня в сердце учение. Добавь ещё 3 юношей и получишь число учеников в моем классе». Сколько учеников у Пифагора? Ответ: 28 учеников.
 Задача Алкуина За сколько прыжков гончая настигнет зайца, если их разделяет расстояние в 150 футов, и у зайца каждый прыжок -на 7 футов , а у собаки – на 9 футов? Справка: 1 фут=30,5 см Ответ: 75 прыжков
 Нестареющие Отечественные задачи
 Задача Кирика Новгородца - Сколько месяцев, недель, дней , часов прожил человек, если в 1136 году ему исполнилось 26 лет.
Ответ: 312 месяцев, 16225 неделей, 113574 дня, 2725786 часов.
 Задача Леонтия Магницкого - Найди число, которое при делении на 2 дает в остатке 1, при делении на 3 – 2, при делении на 4 – 3, а при делении на 5 – остаток 4.
Ответ:59
 И на последок… - Задача о лошади и о муле.
Ответ: лошадь-5 мешкков,мул-7 мешков.
 Спасибо за внимание! multiurok.ru Старинные русские задачи по математике

 Введение Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.
 Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
 Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением. Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач. Задачи исследования: - исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
- исследовать старинный способ решения задач на сплавы и смеси.
 Диофант Его называют отцом алгебры Диофант умел решать очень сложные уравнения, он применял для этого буквенные обозначения и другие приемы. Биографические данные зашифрованы в виде математической задачи, начертанной на его гробнице .
 Задача № 1 Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись: «Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»





Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого. После определения числового выражения - переход на следующий слайд (верхняя кнопка) Попадая повторно на этот слайд повторяем определение буквенных выражений. Далее: Чтобы получить второе определение – нажмите на «Знайку». После определения буквенных выражений нажмите на вторую кнопу и Вы перейдете к практическому заданию.
 Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739) Магницкий Л.Ф. (при рождении Телятин)- русский математик, педагог; преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике (в 1703г. «Арифметика»), которая более ста лет являлась основным учебным пособием по математике в России.
 40-30 30-5 Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять? Параметры исходных продуктов Доли исходных продуктов в конечном продукте Параметры конечного продукта 5% 1-ый продукт 10 частей 30% 25 частей 40% 2-ой продукт Соотношение первого и второго растворов – 10:25 или 2:5.
 Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора? Решение: 2 + 5 = 7(ч) - Сколько грамм приходится на одну часть?
140 : 7 = 20(г) - Сколько грамм 5%-го раствора взять?
2 · 20 = 40(г) - Сколько грамм 40%-го раствора взять?
5 · 20 = 100(г) Ответ: для получения 140г 30%-ного раствора нужно взять 5%-ного раствора 40г, а 40%-ного - 100 г.
 Заключение Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой. Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор. «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич) .
 Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы. В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу. kopilkaurokov.ru Решение "Старинных задач по математике"
 Старинные задачи по математике Выполнила Учитель математики Кронштатова Ирина Юрьевна
 Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль)
 Гипотеза старинные задачи нельзя решать современными методами
 Цель работы - Изучить различные виды старинных задач
- сравнить методы решения задач из первых учебников математики с современными
методами
 Задачи - познакомиться со способами решения старинных задач авторов первых учебников математики;
- решить старинные задачи более привычным для нас способом - путем составления и решения уравнений;
- развивать логическое мышление, умение анализировать, сопоставлять факты, отстаивать свою точку зрения, делать выводы
 Актуальность На сегодняшний день старинные задачи необычны для современного ученика и поэтому позволяют проверить сообразительность и умение решать неординарные задания, мотивируют учащегося на изучение математики
 из истории Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность порешать старинные задачи и сравнить их решение с современным решением
 из истории Наиболее древние письменные математические тексты датируются примерно началом II тыс. до н. э. Математические документы сохранились только в Египте, Вавилоне, Китае и Индии
 Первый печатный учебник математики на русском языке появился в 1703 году. Это была «Арифметика» Леонтия Филипповича Магницкого. 50 лет это был единственный русский учебник математики. М.В.Ломоносов назвал его «вратами всей учености».
 Задача из папируса Ахмеса (Египет, около 2000 г. до н. э.). "Количество и его четвертая часть дают вместе 15". Найди количество. В папирусе Ахмеса задача решается "методом ложного положения". Решение начинается так: "Считай с 4; от них ты должен взять четверть, а именно 1; вместе 5". Однако по условию задачи результат должен быть не 5, а 15, следовательно во сколько раз 15 больше 5, во столько раз неизвестное должно быть больше произвольно взятого числа 4. Так и получается неизвестное 12.
 Решение с помощью уравнения - Пусть х это само число
- Тогда его четвёртая часть это 1/4х или 0,25х
- Составляем уравнение
х +0,25х =15 1,25х = 15 х = 15 : 1,25 х = 12 Ответ: 12
 Задача Пифагора (около 580-501 г. до н.э.) "Рассказывают, что на вопрос, сколько учеников посещают его школу, Пифагор ответил: "Половина изучает математику, четверть - музыку, седьмая часть пребывает в молчании, кроме этого, есть три женщины". Сколько учеников посещало школу Пифагора?"
 Решение пифагорейцев 1-1/2 -1/4 -1/7 =1-25/28 =3/28. Три женщины составляют 3/28 всех учеников школы, значит 3:3/28 =3х28/3 =28. Ответ: 28 учеников .
 Решение с помощью уравнения Обозначим количество всех учеников школы буквой у, тогда 1/2 у+1/4 у+1/7 у +3=у 25/28у +3=у у-25/28 у=3 3/28 у=3 у=3:3/28 у=28 Ответ: в школе Пифагора 28 учеников.
 Как разделить орехи? Из книги Магницкого Л. Ф. 1703 год Говорит дед внукам: «Вот вам 130 орехов. Разделите их на 2 части так, чтобы меньшая часть, увеличенная в 4 раза, равнялась бы большей части, уменьшенной в 3 раза». Как разделить орехи?
 Решение из книги Уменьшив втрое количество орехов в большей части, мы получим их столько же, как в четырех меньших частях. Значит, большая часть должна содержать в 3 x 4 = 12 раз больше орехов, чем меньшая, а общее число орехов должно быть в 13 раз больше, чем в меньшей части. Поэтому меньшая часть должна содержать 130 : 13 = 10 орехов, а большая 130 — 10 = 120 орехов.
 Решение с помощью уравнения - Пусть меньшая часть это х
- Тогда большая часть это 130 – х
- Составим уравнение
(130 – х): 3 = 4х 130 – х = 4х *3 130 –х = 12х 13х =130 Х= 10, 10 орехов меньшая часть, тогда 130-10 = 120 орехов большая часть
 Старинная китайская задача В клетке находится неизвестное число фазанов и кроликов. Известно, вся клетка содержит 35 голов и 94 ноги Узнать число фазанов и число кроликов .
 Логическое китайское решение Представим, что наверх клетки, в которой сидят фазаны и кролики, мы положили морковку. Все кролики встанут на задние лапки, чтобы дотянуться до морковки. Сколько ног в этот момент будет стоять на земле? — 70 (35·2 = 70). — Но в условии задачи даны 94 ноги, где же остальные? — Остальные не посчитаны — это передние лапы кроликов. — Сколько их? — 24 (94 – 70 = 24). — Сколько же кроликов? — 12 (24:2 = 12). — А фазанов? — 23 (35 – 12 = 23).
 Решение с помощью уравнения - Пусть х – это кролики, тогда
(35-х) – это фазаны. - Посчитаем ноги: 4х +2(35 – х) =94
4х +70 – 2х = 94 2х + 70 = 94 2х = 94 – 70 2х =24 Х = 12 т. е. кроликов 12, а фазанов 35 – 12 = 23
 Воз сена из книги Магницкого Л. Ф. Лошадь съедает воз сена за месяц, коза за два месяца, овца за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена.
 Решение из книги Поскольку лошадь съедает воз сена за месяц, то за год (12 месяцев) она съедает 12 возов сена. Так как коза съедает воз сена за 2 месяца, то за год она съедает 6 возов сена. И, наконец, поскольку овца съедает воз сена за 3 месяца, то за год она съедает 4 воза сена. Вместе же они за год съедят 12+6+4=22 воза сена. Тогда один воз сена они вместе съедят за 12:22=6/11 (шесть одиннадцатых) месяца .
 Решение с помощью уравнения Пусть стог сена – это 1. Тогда скорость, с которой лошадь поедает сено 1 стог в месяц У козы скорость1 стог за 2 месяца, т. е. – 1/2 У овцы скорость 1 стог за 3 месяца, т. е. – 1/3 (1 +1/2 + 1/3) *T = 1 T =1 : (1 +1/2 + 1/3) T =1 : 11/6 T =6/11 месяца Ответ : 6/11 месяца
 Занимательные задачи - Задумайте число
- Прибавьте 2
- Результат умножьте на 3
- Вычтите 5
- Вычтите задуманное число
- Умножьте на 2
- Вычтите 1
- Назовите мне результат
 « Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», - писал великий Ньютон в своем учебнике алгебры, озаглавленном «Всеобщая арифметика»
 Метод уравнения
 Результаты - Изучили историю возникновения старинных задач;
- Изучили различные виды старинных задач;
- Сравнили решение старинных задач с современными методами;
- Ознакомились с нетрадиционными методами решения задач.
 Вывод Гипотеза о том, что старинные задачи нельзя решать современными методами не подтвердилась .
 Да, надо математику любить И не считать ученье за мучение! Всё в жизни пригодится, ты учись, Учись и не жалей на то мгновения!
 Источники информации - Олехник С.Н. Старинные занимательные задачи. Москва. 1988г.
- Петраков И.С. Математика для любознательных. Москва. 1990г.
- Депман И..Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5-6 кл. сред.шк. – М.:Просвещение, 1989.
- Нагибин Ф.Ф., Капин Е.С. Математическая шкатулка. Пособие для учащихся 4-8 кл. сред шк. – М.: Просвещение, 1988.
- Перельман Я.И. Занимательная алгебра. М. 1980.
- http://matematika.gym075.edusite.ru/zadachki/denegnir-racheti-1.html
- http://www.pavelbers.com/Arifmetika%20Magnizkogo.htm
- http ://kopilkaurokov.ru /
- http:// igraemsdetmy.ru
- http://uslide.ru /
 Благодарю за внимание multiurok.ru Решение старинных задач различными способамиСлайд 1 Работу выполнили Ильин Дмитрий и Яшин Кирилл, ученики 8-ого класса Руководитель: Жилова З.Г., учитель математикиСлайд 2 Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений. Введение Слайд 3 Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них. Слайд 4 Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением. Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач. Задачи исследования: исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом исследовать старинный способ решения задач на сплавы и смеси. Слайд 5 Диофант Его называют отцом алгебры Диофант умел решать очень сложные уравнения, он применял для этого буквенные обозначения и другие приемы. Биографические данные зашифрованы в виде математической задачи, начертанной на его гробнице . Слайд 6 Задача № 1 Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись: «Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?» Слайд 12 Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого. Слайд 13 Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739) Магницкий Л.Ф. (при рождении Телятин)- русский математик, педагог; преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике (в 1703г. «Арифметика»), которая более ста лет являлась основным учебным пособием по математике в России. Слайд 14 Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять? Параметры конечного продукта Параметры исходных продуктов Доли исходных продуктов в конечном продукте 30% 5% 40% 40-30 30-5 1-ый продукт 2-ой продукт 10 частей 25 частей Соотношение первого и второго растворов – 10:25 или 2:5. Слайд 15 Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора? Решение: Сколько всего частей? 2 + 5 = 7(ч) Сколько грамм приходится на одну часть? 140 : 7 = 20(г) Сколько грамм 5%-го раствора взять? 2 · 20 = 40(г) Сколько грамм 40%-го раствора взять? 5 · 20 = 100(г) Ответ: для получения 140г 30%-ного раствора нужно взять 5%-ного раствора 40г, а 40%-ного - 100 г. Слайд 16 Заключение Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой. Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор. «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич) . Слайд 17 Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы. В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу. nsportal.ru Решение старинных задач на дроби Муниципальное бюджетное общеобразовательное учреждение «Абазинская средняя общеобразовательная школа №5». Решение старинных задач на дроби Автор: ученик 5 «б» класса Дресвянников Никита Руководитель: учитель математики Алёнина Нина Ивановна. г. Абаза – 2014 г. Содержание: 1 . введение 2 из истории возникновения дробей 3. старинные задачи на дроби 4. заключение 5 . используемая литература Введение Уважение к минувшему - вот чёрта, отличающая образованность от дикости. А.С.Пушкин В этом учебном году на уроках математики мы познакомились с обыкновенными дробями. Мы научились решать различные задачи по этой теме. Меня заинтересовали задачи из раздела (Для тех, кому интересно) и я стал решать задачи самостоятельно. Потом я попробовал решить задачи, предложенные учителем. Особенно мне понравились старинные задачи на дроби. Меня заинтересовали эти задачи в первую очередь своей необычной формулировкой и необычным рассуждением при решении. Занимаясь этой темой, я изучил теоретический материал: историю возникновение дробей, познакомился с древними математиками. На практике я научился решать старинные задачи на дроби разными способами. Цели моей работы Знакомство со старинными историческими задачами. Изучение нестандартных способов решения задач.
Задачи: 1.Собрать из различных источников старинные задачи. 2.сравнить старинные задачи с современными способами решения. Из истории возникновения дробей. Первой дробью, с которой познакомились люди, была половина 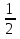 . Старейшим математическим документом является (Московский папирус ) который был написан в Древнем Египте около 4 тыс. . Старейшим математическим документом является (Московский папирус ) который был написан в Древнем Египте около 4 тыс. лет назад и хранится в Московском музее изобразительных искусств. Из этого документа выяснилось, что для обозначения дробей раньше использовали особые знаки, а все остальные дроби старались записать как сумму дробей. Это было очень неудобно. Интересная система дробей был в Древнем Риме. Она основывалась на деление единиц веса на 12 долей и называлась унцией. Всего принималось 18 различных названий дробей. Чтобы работать с дробями, надо было хотя бы запомнить их названия, таблицу сложения, таблицу умножения. В греческих сочинениях по математике дробей не встречалось. Греческие учёные считали, что математика должна заниматься только целыми числами, а возится с дробями должны были только купцы, ремесленники, астрономы, землемеры и другой чёрный люд. Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Записывать дроби в точности, как сейчас, стали арабы. А к способу записи десятичных дробей люди шли ещё дольше. И только в 15 веке в работе Каши: «Ключ к искусству счета» появилось изложения о десятичных дробях. Сейчас нам кажется: как всё это просто. Старинные задачи на дроби. В древних рукописях и старинных учебниках арифметики разных стран, встречается много интересных задач на дроби. Решение каждой из них требует немалой смекалки и сообразительности, умения рассуждать. задача №1 Есть кадамба цветок, На один лепесток Пчёлок 5 часть опустилась Рядом тут же росла. Вся в цвету селенга И на ней 3 часть поместилась Разность их ты найди Её трижды сложи И тех пчёл на Кутай посади Толька 1 не нашла Себе место нигде, Всё летала то взад, то вперёд и везде. Ароматом цветов наслаждаясь Назови теперь мне Подсчитавши в уме, Сколько пчёлок всего здесь собралось? Решение 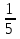 + + 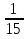 = =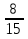 (часть пчёл сидит на цветах) (часть пчёл сидит на цветах)
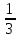 - - 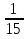 = =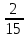 (разность) (разность)
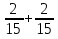 + +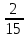 = =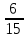 ; ; 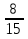 + +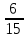 = =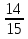 ; 1 ; 1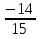 = =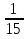
(ответ: 15 пчёлок всего) задача №2 Слониха, слонёнок и слон пришли к озеру, чтобы напиться воды. Слон может выпить за 3 часа, слониха за 5 часов, а слонёнок за 6 часов. За сколько времени они выпьют озеро, если будут пить вместе. 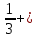 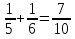 (за 1 час вместе) (за 1 час вместе)
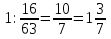
Ответ: за 1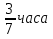 задача№3 (Китай 2в н.э.) Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и гусь вылетают одновременно. Через сколько дней они встречаются? Решения: 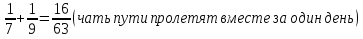
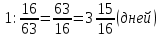 Ответ: за 3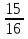 задача №4 Для переписки сочинения наняты четыре писца. Первый мог бы перепасть сочинения в 24 дня, второй - в 36 дней, третий - в 20 дней, четвёртый – в 18 дней. Какую часть сочинения перепишут они в один день, если будет работать вместе? За сколько времени они, работая вместе, перепишут сочинения? 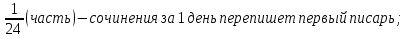
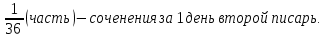 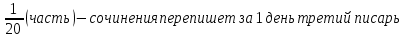
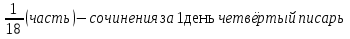
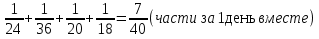
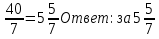 дня перепишут вместе. дня перепишут вместе.
Задача №5 Из папируса Ахмеса (Египет, около 2000 лет до н.э.) Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты из своего многочисленного стада? Пастух отвечает: -Я привожу две трети скота. Сочти сколько быков в стаде. Решение: 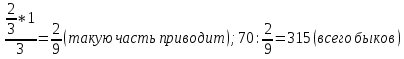
Ответ:315 быков задача №6 (Древняя Греция ,1 в. До н. э.) Бассейн может заполнять через четыре фонтана. Если открыт только первый фонтан, бассейн наполнится за день, только второй за два дня. Только третий за три дня, только четвёртый за 4 дня. За какое время наполнится бассейн, если открыты все четыре крана? Решение: Посмотрим, сколько бассейнов могут заполнить фонтаны за12 дней. Первые 12 бассейнов Второй 6 бассейнов. Третий четыре бассейна Четвёртый 3 бассейн. Значит, всего они могут заполнить бассейнов за 12 дней 12+6+4+3=25. Поэтому один бассейн вместе они заполнят за 12:25=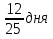 Ответ: 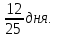 Задача №7 Из  Л.Ф. Магницкого (Россия 18 век) Л.Ф. Магницкого (Россия 18 век) Лошадь съедает воз сена за меся, коза за два месяца , овца за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена? Решение: За 6 месяцев лошадь съест 6 возов сена, коза 3, а овца 2 воза, вместе всего съедят 11 возов сена. А один воз сена они вместе съедят за 6/11 месяца (число 6 делится на 2 и на3) Ответ: за 6/11 месяца. задача №8 В знаменитой книге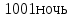 мудрец задаёт юной деве следующую задачу: Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей отдала половину сорванных яблок. Также она поступила с третьим стражником, то неё осталось лишь 10 яблок. Сколько яблок она собрала в саду? мудрец задаёт юной деве следующую задачу: Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей отдала половину сорванных яблок. Также она поступила с третьим стражником, то неё осталось лишь 10 яблок. Сколько яблок она собрала в саду? 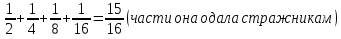
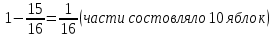 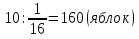 Ответ: 160 яблок Старинная задача №9 Путник, догнав другого, спросил его: «далеко ли до деревни, которая впереди?». Другой путник ответил: «Расстояние от деревни, из которой ты идёшь, равно трети всего пути всего расстояния между деревнями. А если пройдёшь ещё 2 версты, будет ровно посередине между деревнями». Сколько вёрст осталось идти путнику? Решение: Две версты, которые нужно пройти первому путнику до середины между деревнями, составляют пути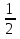 -1/3=1/6 часть все -1/3=1/6 часть все расстояния между деревнями. Значит расстояние между деревнями в 6 раз больше и равно 2* 6=12верс. Так как к моменту встречи путник прошёл треть пути, т.е. 12*1/3=4 версты, ему осталось пройти 12-4=8 вёрст. Ответ:8 вёрст Заключение Выполняя данную работу, я научился решать задачи новыми, очень интересными для меня способами. Они оказались очень занимательными и поучительными. Также я сделал вывод, что можно решать задачи даже с помощью рассуждений. Главный вывод в моей работе заключается в том, что я нашёл несколько способов решения задач (задачи в частях, задачи на совместную работу, нахождения части от части, задачи на рассуждения). С данной работой я познакомил своих одноклассников. Они также с увлечением решали старинные задачи. Литература: 1.Дорофеев Г.В,Шарыгин И. Ф, Суворова С.Б и другие. Математика 5 класс Просвещение 2010г 2 Виленкин Н.Я, Жохов В. И, Чесноков А. С. Шварцбурд С. И. Математика 5 класс. Мнемозина 2013г. infourok.ru
|
