Искусство Древнего мира. Древний счет майя
Майянисты говорят: Система Длинного Счета Майя Длинный Счёт, для которого мы не знаем названия на древнем языке Майя, считается линейной системой счёта дней. В действительности, эта система состоит из вложенный друг друга циклов, из которых самый большой составляет 5126 лет. Таким образом, он проходит через всю историю древней цивилизации Майя.  Трес Сапотес, 31 г. до н.э. Но на настоящее время самыми старыми, четко определёнными записями дат в системе Длинного Счета являются стела из городища Трес Сапотес с датой, соответствующей 31 году до н.э., и Чиапа де Корсо - 36 год до н.э. которые были построены отнюдь не Майя а... Ольмеками. Самая ранняя дата из классической эпохи Майя находится в Тикале и соответствует 292 году н.э. - то есть более, чем на 300 лет позже. Самой последней записанной Длинным Счётом датой в настоящее время является стела из Ишлу в Петене, Гватемала. Она соответствует 910 году н.э. и считается окончанием классического периода цивилизации Майя. Здесь следует отметить, что сами археологи считают, что открыли и раскопали не более десяти процентов возможных городов и строений на территории Месоамерики. Указанные выше стелы демонстрируют уже сформировавшуюся систему записи Длинного Счёта. И это означает, что она была разработана гораздо раньше. Как и наш современный календарь, календарь Длинного Счёта имеет начальную дату. Наш начинается 1 января 0 года, а их, как считается, 11 августа 3114 года до н.э. Но в отличие от нашего общепринятого календаря, календарь Длинного Счета имеет, как многими ошибочно считается, и дату окончания - 21 декабря 2012 года н.э. Длинный Счёт представлен в виде пятиразрядной системы вложенных циклов: - кин (один день)
- виналь (20 дней, месяц)
- тун (13 виналей, 360 дней, год)
- катун (20 тунов)
- бактун (20 катунов)
Интересно отметить, что "год" в Длинном Счёте составляет 360 дней, а не 365 солнечных дней, отражённых как в нашем общепринятом календаре, так и в календарном цикле Хааб у Майя. И уж тем более не 365,2425 - более точного числа дней в году, отраженного, в частности, в григорианском календаре. Таким образом, Длинный Счёт расходится с циклом Хааб на 5 дней за год, и на 5,2425 дней с тропическим годом. Знали ли об этом создатели Длинного Счёта? Да, знали! Но Длинный Счет, по-видимому, был создан не для точного следования годичным сезонным периодам, а исключительно как особый счёт дней в виде больших циклов. Самый большой из пяти циклов, бактун, составляет 400 тунов. Многие полагают, что Длинный Счёт завершится по истечении 13-ти бактунов с момента создания нашего мира, обозначенного как Четвертое творение в майянской истории о сотворении мира - Пополь Вух. Эти 13 бактунов завершаются как раз 21 декабря 2012 года по нашему календарю. Что так привлекает интересующихся "пророчествами о конце света". Чтобы понять, как происходит смена циклов в системе Длинного Счёта, посмотрим, как это происходило в день творения и в день завершения: | 12.19.19.17.19 |
3 Кавак 7 Кумку |
10 августа 3114 г. до н.э. |
| 13.0.0.0.0 |
4 Ахау 8 Кумку |
11 августа 3114 г. до н.э. |
| 0.0.0.0.1 |
5 Имиш 9 Кумку |
12 августа 3114 г. до н.э. |
| |
|
|
| 12.19.19.17.19 |
3 Кавак 2 Канкин |
20 декабря 2012 г. н.э. |
| 13.0.0.0.0 |
4 Ахау 3 Канкин |
21 декабря 2012 г. н.э. |
| 0.0.0.0.1 |
5 Имиш 4 Канкин |
22 декабря 2012 г. н.э. |
В действительности среди специалистов ходят споры, как функционирует Длинный Счёт и представлены числа после 13-го бактуна. Некоторые полагают, что нумерация бактунов не обнуляется до 0.0.0.0.1, но продолжается как 13.0.0.0.1, 13.0.0.0.2 и далее до конца 13-го бактуна, который уже записывается, как 1.0.0.0.0. Поскольку эти даты нигде не были записаны самими Майя (или их не нашли), вопрос остаётся открытым. Другая точка зрения на способ записи Длинного Счёта утверждает, что число бактунов не обнуляется после 13-ти, но продолжается до 20-ти, как остальные разряды длинного счёта. Исключение составляет количество виналей - их 18, что соответствует счёту дней в Хааб, где солнечный год представлен, как 18 месяцев по 20 дней в каждом. Сэр Эрик Томпсон, один из наиболее известных майянистов прошлого века, исследовавший систему Длинного Счёта всю свою жизнь, был убеждён, что количество бактунов в большом цикле должно быть 20, а не 13. Он логически обосновывал это так: Я везде предполагал, что бактуны группируются по 20, а не по 13, и подтверждение двадцатеричного счёта бактунов есть и в Дрезденском кодексе, и в записях дат Паленке и Копана, что невозможно отрицать. Я полагаю, что на раннем этапе, когда был изобретён Длинный Счёт, самым большим периодом был бактун, и бактуны группировались в повторяющемся цикле по 13. Но в последующем стремлении расширить учитываемый диапазон времени были введены более долгие периоды, такие, как пиктун. С таким расширением календаря было важно сделать счёт бактунов двадцатеричным. Соответственно, 20 бактунов формируют один пиктун, но дата 4 Ахау 8 Кумку стала настолько прочно связана с окончанием календарного цикла в 13 бактунов, что до сих пор используется в качестве точки отсчёта, хотя для целей вычисления дат следует использовать цикл из 20 бактунов" Томпсон упоминает важный факт, который редко принимается во внимание при популярном обсуждении календаря Длинного Счёта - факт того, что Майя записывали даты, используя циклы длиннее бактуна. Вот некоторые из них, известные в настоящий момент: | Пиктун |
20 Бактунов |
8000 тунов |
2,880,000 дней |
~7,885 лет |
| Калабтун |
20 Пиктунов |
160,000 тунов |
57,600,000 дней |
~157,703 года |
| Киничильтун |
20 Калабтунов |
3,200,000 тунов |
1,152,000,000 дней |
~3,154,068 лет |
| Алаутун |
20 Киничильтунов |
64,000,000 тунов |
23,040,000,000 дней |
~63,081,377 лет |
Имена этих циклов условные. До сих пор неизвестно, как они назывались во времена использования Длинного Счёта. Эти большие циклы не так уж и редки в надписях. Они появляются много раз в Дрезденском кодексе, и на стелах и надписях в Паленке, Копане, Киригуа, Тикале, Яшчилане и Коба. Само существование этих больших циклов поднимает вопрос о том, действительно ли Длинный Счёт обнуляется по прошествии 13-ти бактунов? И если да - то зачем тогда ввели большие циклы? При обсуждении вопроса длительности счета бактунов часто используют пример из Паленке в качестве аргументов в защиту двадцатеричной системы:  Западная стена Храма Надписей в Паленке. Рис. Линда Шеле. Текст Западной стены из Храма Надписей упоминает дату рождения Пакаля, и ведёт счет дальше в будущее для достижения цикла в один пиктун. Вот расшифровка текста: | 9.8.9.13.0 |
8 Ахау13 Поп |
24 марта 603 г. н.э. |
Рождение Пакаля |
| + |
| 10.11.10.5.8 |
Текст указывает о прошествии многих дней в будущем... |
| ...Прибывает к: |
| (1.0.0.0.0.8) |
5 Ламат 1 Моль |
Текст говорит 1 пиктун 8 кинов |
| И далее упоминается дата через календарный цикл длительностью ровно в один пиктун: |
| (1.0.0.0.0.0) |
10 Ахау13 Яшкин |
13 октября 4772 г. н.э. |
Можно увидеть, как удалённая в будущее дата 10.11.10.5.8 была намеренно выбрана так, чтобы привести к круглой дате в завершении цикла, с нулями в разрядах. Если бы цикл бактунов завершался после 13, тогда следующая дата была бы 1.7.0.0.0.8, а не 1.0.0.0.0.8. Зачем же было обозначать такие удалённые в будущее даты в связи с именем Пакаля, правившего в Паленке в VII веке н.э.? Возможно, это было указание на бессмертность его души? Его будущее возрождение? Теорий на этот счёт много. Интересно, что календарный цикл 5 Ламат 1 Моль является также датой восхождения на трон в 612 году н.э., и 5 Ламат 1 Моль появляется в тексте ровно через 80 календарных циклов (через 52 солнечных года). Поскольку Пакалю было около 80-ти лет, когда он умер, возможно это поэтическое указание его преклонного возраста.  Храм Креста, Паленке, Так что если у нас есть четкие доказательства того, что бактун, как и все остальные позиции Длинного Счёта, за исключением виналей, работает в циклах по 20, то почему так много людей считают, что он сбросит счёт по достижении 13-ти в 2012 году? Ответ лежит в западной логике математических предположений, что если Длинный Счет начался в 13-м бактуне, то и закончится он должен в 13-м бактуне. Когда человек из западной культуры представляет себе цикл, то он сразу же вызывает в воображении образ часов с вращающейся стрелкой, начинаясь и заканчиваясь на 12-ти. Но должно ли быть именно так? Часть проблемы заключается в предположении, что современные западные и древние Центрально-американские понятия "цикл" отражали одно и то же. Существуют надписи в Паленке, Копане и Киригуа, которые датируют особые события, произошедшие до начала текущей эры Длинного Счёта. Все они заявляют, что они произошли в течение 12-го бактуна и пришли к 13.0.0.0.0 4 Ахау 8 Кумку. В Паленке, тексты в храмах Группы Креста говорят, что 9 декабря 3121 до н.э. родилась женщина по имени Муан Мат. Спустя 754 года, уже после начала нынешней эпохи 11 августа 3114 г. до н.э., а именно 23 октября 2360 г. до н.э., она родила божество GI из так называемой Триады Паленке. Эти данные охватывают дату создания, начиная с 12-го бактуна и переходят обратно в 1-й бактун. Вот как эти даты расположены в тексте: | 12.19.13.4.0 |
8 Ахау18 Сек |
9 декабря 3120 до н.э. |
Рождение Муан Мат |
| 13.0.0.0.0 |
4 Ахау8 Кумку |
11 августа 3114 до н.э. |
Дата Творения |
| 1.18.5.3.7 |
13 Кими19 Кех |
23 октября 2360 до н.э. |
Рождение GI |
Эти даты даны в полной записи Длинного Счёта, а не как периоды времени от начальной даты (дистанционные номера), или календарные циклы, как это обычно принято в текстах Майя. Казалось бы, эти доказательства достаточно убедительны, но эти несколько текстов являются единственным примером из всего мира Майя, который убедил западных исследователей, что Длинный Счёт снова обнулится в 2012 году. В действительности, хотя у нас есть много примеров записи 13.0.0.0.0 на 11 августа 3114 г. до н.э., есть только один известный текст, чтобы записать дату 13.0.0.0.0 на 21 декабря 2012 года н.э.. Он был найден на монументе номер 6 из Тортугеро и дальнейший текст разрушен сразу после упоминания даты, скрывая событие, которое должно произойти в этот день. Для древних Майя, 13-й бактун закончился в начале эпохи четвертого сотворения мира. Пополь Вух описывает три предыдущих эпохи и судьбы их обитателей, но не указывает точные даты. Ацтеки спустя столетия использовали очень похожие концепции и объяснили это первым испанцам в некоторых деталях. Ацтеки полагали, что живут в пятую эпоху создания, а не в четвёртую. Некоторые исследователи полагают, что ацтеки, возможно, считали крах классической цивилизации майя в 9-м веке завершением четвёртой эпохи. Ацтеки указывали промежутки времени для каждой из предыдущих эпох. Что интересно - они не одинаковы. Вот их данные для предыдущих эпох: | Первое Солнце |
13 циклов по 52 года, всего 676 лет |
| Второе Солнце |
7 циклов по 52 года, всего 364 года |
| Третье Солнце |
6 циклов по 52 года, всего 312 года |
| Четвертое Солнце |
13 циклов по 52 года, всего 676 лет |
 Календарнай камень Ацтеков. Если сложить длины второй и третьей эпохи вместе, то получаем еще один набор из 13 х 52 лет, как для 1-й и 4-й эпох. Как и для Майя, для Ацтеков, похоже, понятие 13-ти циклов было связано с завершением эпохи или существования мира. Для нынешней эпохи не была указана продолжительность, но было предсказано, что она будет в конечном итоге разрушена землетрясениями. Учитывая разницу в прошлых длительностях циклов, нельзя с уверенностью предположить, что нынешняя эпоха Ацтеков будет 13 х 52 лет. Означает ли это, что то же самое не относится к понятию длительности эпохи Майя? Часть ответа может находиться в концептуальном различии между понятиями "цикл" и "эра". Существуют определенные регулярные циклы в календаре Майя, и их взаимная смена зависит друг от друга. Кин, виналь, тун и катун являются неизменными циклами времени. Западный календарь имеет такой же циклический шаг - в день, год, век, тысячелетие и т.д. Однако, «эра» в западном мышлении редко соответствует точному счёту календарного цикла. Железный век, эпоха Возрождения, индустриализация - каждый из них был разный "эрой" в истории со своей уникальной продолжительностью. Была ли такая же концептуальная разница у Майя, когда они писали, что 13 бактунов означают конец "эры"? Существует причина полагать, что число 13 было использовано как символический способ сказать "завершение". Существуют тексты в городах Йашчилан, Коба, а также в Дрезденском кодексе, которые описывают даты в системе Длинного Счёта, в которых много циклов больше бактуна повторяют номер 13 в качестве коэффициентов. Например, в Йашчилане, на панели в передней части храма номер 33, размещены десять позиций по 13 над указанной датой: 13.13.13.13.13.13.13.13.13.13.9.15.13.6.9 - 19 октября 744 года н.э.  Кобан, Стела 1 В городе Коба на стеллe номер 1 размещено, по крайней мере, двадцать позиций по 13 на дату создания, 13.0.0.0.0 11 августа 3314 г. до н. э. Если бы мы попытались подсчитать все эти циклы по 13 в качестве фактических коэффициентов, каждый из которых повышает разряд при достижении 20-ти циклов, то мы получили бы 41.943.040.000.000.000.000.000.000.000.000 лет в прошлое! Дрезденский кодекс на странице 52 также записывает дату с 13-ю последовательных циклов по 13. Поскольку ни один из этих 13-ти циклов не имеет эффекта на нижние циклы, не похоже, что они были размещены там для фактического расчёта. Они, вероятно, больше символически утверждали, что-то типа "многие циклы прошли". Если эти коэффициенты по 13 пиктунов, калабтунов, киничильтунов и т.д. символизируют "давно прошедшие дни", то почему бы и 13-ти бактунам не символизировать то же самое? Таким образом, если идея о том, что 13 бактунов это конец нашей эры, ставится под сомнение, то что мы должны думать о наступлении этого момента в 2012 году нашей эры? Хотя тексты Майя ничего не говорят о том, что может произойти при окончании 13-го бактуна, мы знаем, что окончание каждого бактуна считалось временем больших перемен. Анализ истории древних Майя дает общее понимание этого понятия. Следующие события, произошедшие на рубеже последних пяти бактунов, хоть и не отражают глобальных перемен, но, тем не менее, дают общую картину: - Начало 8-го бактуна (41 год н.э.)Последние из городов Ольмеков, некоторые из которых насчитывали более 1000 лет непрерывного обитания, окончательно покидаются жителями и никогда снова не заселяются.
- Начало 9-го бактуна (435 год н.э.)Теотиуакан, государство-мегаполис древних Тольтеков Центральной Мексики, начинает оказывать своё влияние на мир Майя, основывая новые города, создавая династии правителей и совершая военные кампании.
- Начало 10-го бактуна (830 год н.э.)Окончание Классического периода цивилизации Майя. Жители почти одновременно покидают более ста крупных городов, объяснения чему до сих пор не найдено.
- Начало 11-го бактуна (1224 год н.э.)Упадок города Чичен-Итца на полуострове Юкатан. Начало расцвета города Майяпан.
- Начало 12-го бактуна (1618 год н.э.)Последнее независимое государство Майя - Итца на озере Петен, высылает своих эмиссаров колониальным властям Новой Испании с заявлением, что они принимают новый порядок в соответствии с наступающим новым циклом.
...Это было во времена завершения последнего бактуна, когда испанцы завоевали озеро Петен и захватили правителя Кан Эк, что даёт нам особое понимание представлений Майя о смене бактунов. В год 1617, Кан Эк послал своих эмиссаров в Мериду сообщить испанским властям, что 12-й бактун наступает, и что они готовы к тем изменениям, которые это принесет. Испанцы расценили это, как желание индейцев перейти в христианство, и началась настоящая гонка между различными миссионерскими группами, чтобы прослыть первыми, кто сумел покорить могучий и непримиримый народ Итца. Со священниками пришли и воины, а с ними и неизбежный конец. Хотя Итца, вероятно, не планировали свою смерть, они были правы, что время больших перемен для них наступило. В заключение можно сказать, что хотя в точности неизвестно, что отмечает сброс Длинного Счёта в 2012 году, совершенно понятно, что он означает смену бактуна. Древние Майя посчитали бы это временем больших изменений. Так же, как и смена предыдущих бактунов отмечалась великими переменами, и 13-й бактун должен иметь особое значение, возможно, начало новой эры в мировой истории. Время покажет... - Начало 13-го бактуна (2013 год н.э.)Перемены только начинаются...
Перевод © Сергей Рословец Это было мнение учёных, занимающихся тематикой цивилизации Майя. Что говорят сами наследники Традиции Майя можно прочитать далее » www.toltec.ru Числа и даты | Календарь майя | Стюфляев МаксимПрежде чем перейти собственно к календарю, имеет смысл кратко рассказать об используемых древними майя способах записи чисел. В отличие от арабов и европейцев, майя применяли не десятеричную, а двадцатеричную систему счисления, то есть основой их счета была двадцатка.[i] Если мы группируем единицы в десятки, сотни и тысячи, то у майя аналогичное значение имели числа 20, 400 (20 раз по 20), 8000 (20 раз по 400), 160000 (20 раз по 8000) и так далее до бесконечности.[ii] Необычность этой системы, а также то, как легко майя ориентировались в ней, поразили Д. де Ланду: «При этих возвращениях и запутанном счете удивительно видеть свободу, с которой те, кто знают [их], считают и разбираются».[iii] 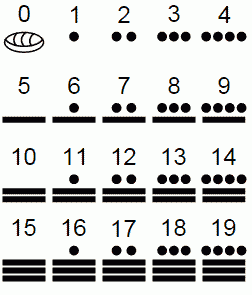
Цифры майя. Крупным интеллектуальным достижением майя стало самостоятельное изобретение нуля. Для сравнения уместно напомнить, что европейцы и арабы переняли нуль из Индии, а в Римской империи такое понятие не было известно. Записывать числа майя могли при помощи двух видов знаков. Наиболее распространена была простая форма записи чисел, для которой использовались всего несколько цифр: нуль в форме раковины,[iv] точка-единица, пятерка, имевшая вид горизонтальной черты, а также особые иероглифы для чисел, делившихся без остатка на двадцать (20, 8000).[v] Числа от 0 до 19 записывались сочетанием этих знаков, например, число 3 писалось как три точки, а 19 как три черты и четыре точки над ними. Для записи больших чисел майя, как и арабы, использовали позиционную систему счета, то есть принадлежность цифры к тому или иному разряду чисел (единицы, двадцатки, четырехсотки и так далее) определялась ее порядковым положением. Но если в привычной для нас системе разряды увеличиваются справа налево, то майя в большинстве случаев записывали их в вертикальный столбец снизу вверх. Примеры позиционного счета представлены на картинке ниже. Число 20 записано как 1 в разряде двадцаток (одна двадцатка) и 0 в разряде единиц. Число 806 записано как 2 в разряде четырехсоток (два раза по четыреста), 0 в разряде двадцаток и 6 в разряде единиц. 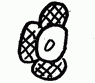 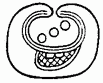 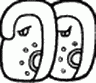
MIH («Нуль») WINIK («Двадцать») PIK («Восемь тысяч») Логограммы (знаки-слова), использовавшиеся в иероглифической письменности майя для обозначения некоторых чисел. В классический период для записи календарных дат Долгого счета помимо линий и точек иногда использовались так называемые «лицевые знаки». Каждое число от 0 до 20 имело свою особую «лицевую» форму, представленную в виде головы того или иного божества. Например, обозначением числа 10 могла служить голова бога смерти. По-видимому, это говорит о том, что майя воспринимали числа не как абстрактные единицы счета, а как живых существ и верили, что у каждого числа имелся свой бог-покровитель. Представления о богах-покровителях чисел были известны в Центральной Мексике. Следует отметить, что особые лицевые знаки существовали для цифр от 0 до 13, остальные – это сочетание цифры 10 и цифры, которая в сумме с десяткой дает соответствующее число.[vi] 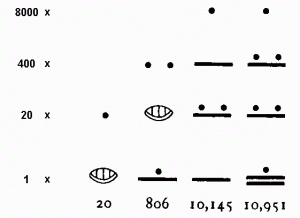
Примеры позиционного счета, применявшегося древними майя. Как и любой другой народ, майя записывали числа для решения самых разных задач. Цифрами оперировали при организации земледельческих работ, ведении торговли, подсчете дани, которая поступала ко двору правителя и так далее. Одна из важнейших функций чисел заключалась в том, что они использовались для записи дат майяского календаря. 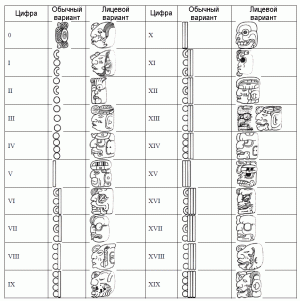
Лицевые формы цифр в виде изображений различных богов ("Введение в иероглифическую письменность майя". Талах В.Н. Киев, 2010). [i] Она, вероятно, родилась из наблюдений за телом человека, ведь на руках и ногах у людей двадцать пальцев. В подтверждение данного предположения можно отметить, что число 20 и пон www.indiansworld.org Математические системы исчисления майя | Искусство Древнего мира Майя записывали свои числа в виде комбинаций точек и тире, причём точки обозначали единицы данного порядка, а тире — пятёрки. Писались цифры не горизонтально, а вертикально — снизу вверх.Ноль майя изображали отдельным знаком в виде стилизованной раковины, и использовали, в том числе, и для записи других чисел — например, число 20 изображалось как одна точка и знак нуля.  Цифры майя от 0 до 19 Каждый последующий порядок отличался от нижнего в 20 раз (в арабской системе исчисления порядки отличаются на 10).В этой стройной двадцатиричной системе было одно исключение: если прибавить к 359 единицу, полученное число (360) становится первичным числом третьего порядка (а это должно было бы быть 20×20=400!).  Так записывались числа больше 20 индейцами майя Вероятно, это связано с тем, что основной областью применения математики была астрономия, и таким образом майя решили проблему приспособления двадцатеричной системы счисления к её нуждам, максимально приблизив первичное число третьего порядка к числу дней в календарном году, ведь в 18 месяцах хааба 360 дней. При вычислениях бóльших чисел майя снова возвращались к «строгой» двадцатиричной системе, и каждый последующий разряд цифр обозначал двадцатикратное умножение числа. Похожие записи
ancientart.ru Система счета у Майя. | Социальная сеть работников образованияСлайд 1 Система счёта древних племён Майя Подготовила: ученица 5 «А» класса Смирнова Ксения Руководитель: Кусакина Л.А.Слайд 2 МА́ЙЯ — цивилизация Мезоамерики , известная благодаря своей письменности, искусству, архитектуре, математической и астрономической системам . Существовали приблизительно с 2000 года до н. э. по 250 год н. э. Слайд 3 Создали эффективную систему земледелия, имели глубокие знания в области астрономии . Потомками древних майя являются не только современные народы майя , сохранившие язык предков, но и часть испаноязычного населения южных штатов Мексики и Гватемалы Слайд 4 Первыми, кто изобрел систему нумерации с цифрой "0", были как раз представители этого народа. Слайд 5 Система счёта у майя базировалась не на привычной десятичной системе, а на двадцатиричной. Истоки лежат в методе счёта, при котором применялись не только десять пальцев рук, но и десять пальцев ног. При этом существовала структура в виде четырёх блоков по пять цифр, что соответствовало пяти пальцам руки и ноги. Также интересным является тот факт, что у майя существовало обозначение нуля, который был представлен в виде пустой раковины от устрицы или улитки. Слайд 6 Запись числа производилась всего лишь при помощи трёх элементов: единица — точка, пять — черта, нуль — раковина. Наличие нуля в счёте майя является свидетельством того, что развитие математики народа стояло на высоком уровне. Система счёта майя представлена двадцатеричной счисления . Слайд 7 Запись происходила вертикально, причём первый разряд находился внизу, второй — выше первого, третий — выше второго. В нижней части числа заканчивались на 19-ти , и далее над ним ставилась точка, обозначающая единицу. Число двадцать можно было представить как раковина (нуль) и точка (двадцать) над ней. Слайд 8 Диего де Ланда , автор книги «Сообщение о делах в Юкатане» ( 1566 ), содержащей много ценной информации о цивилизации майя , отмечал необычайный уровень развития у индейцев , способных оперировать большим количеством чисел. nsportal.ru ДЛИТЕЛЬНЫЙ СЧЕТ МАЙЯ. Тайны Майя ДЛИТЕЛЬНЫЙ СЧЕТ МАЙЯ Одним из достижений культуры майя (в отличие от более поздней, ацтекской) было умение обращаться со своим довольно сложным календарем. Сейчас на Западе мы пользуемся григорианским календарем (модернизированный вариант юлианского), в котором отсчет времени ведется применительно к одному событию, к Рождеству Христову, которое произошло, так сказать, в нулевой год н. э. Все предыдущие годы отнесены к периоду до нашей эры, последующие относятся к нашей эре. Пользуясь нашим календарем, мы можем датировать любые события прошедших эпох, а также — будущие годы. Мы уже настолько привыкли к своему григорианскому календарю, что порой забываем о том, что он не единственный, которым пользуются в современном мире, и что люди не пользовались им в далеком прошлом. Что до жителей Центральной Америки, то до испанского завоевания они, конечно, вели счет времени не от Рождества Христа, а от другого события — от «Рождения Венеры». Красавица богиня из европейской мифологии тут ни при чем. Имелся в виду «первый восход» — появление на небесах планеты Венеры. Майя были великими астрономами и вели систематические наблюдения за движением планеты Венеры по орбите, что и составило основу сложной календарной системы, просуществовавшей много столетий. Открытию календарной системы, основанной на Длительном счете индейцев майя, мы обязаны во многом трудам немецкого библиотекаря Эрнста Фёр-стемана. С 1867 года он начал работать в Дрезденской библиотеке, и так случилось, что именно в этой библиотеке хранился самый значительный сборник документов, касавшихся майя — так называемый Дрезденский кодекс. В 1880 году Фёрстеман начал серьезно изучать этот сборник. Прежде всего, он начал делать очень точные факсимильные копии и изготовил их 60. Это оказалось кстати, потому что оригинал сильно пострадал от воды при хранении в винном погребе во время Второй мировой войны. Уже в 1882 году американец Сайрус Томас, изучая фотографию одной надписи, заключил, что цифры майя следует читать слева направо и сверху вниз. Фёрстеман, работая с Дрезденским кодексом и с «Сообщением» Ланды, продолжил эту работу, и ему удалось разъяснить загадки календаря майя. Немецкий исследователь установил, что их счет времени основывался не на десятичной, как у нас сейчас, а на двадцатичной системе, что майя фиксировали даты с помощью Длительного счета и что начало большого календарного цикла у них приходилось на 4 ахау, 8 куму не одну тысячу лет назад. Чтобы это понять, необходимо усвоить еще кое-что из представлений майя о счете времени. Помимо пользования «тцолкином» (год из 260 дней), «нечетным годом» (из 365 дней) и календарным циклом в 52 года, майя вели также особый счет дням. С небольшими вариациями, они пользовались своей двадцатичной системой, считая время в «кинах», «уиналах», «тунах» и т. д. Эта система, на первый взгляд, может показаться очень громоздкой, но это не так, если помнить о двадцатичной системе исчисления времени. Принцип ее выглядел так: 20 кинов-дней = 1 уиналу (20-дневный месяц) 18 уиналов = 1 туну (360-дневный год) 20 тунов = 1 катуну (7200 дней) 20 катунов = 1 бактуну (144 000 дней) На стелах и других памятниках даты майя были записаны двумя колонками иероглифов, читаемых слева направо и сверху вниз. Вся серия начиналась с вводного иероглифа и часто кончалась датой, имевшей отношение к лунному циклу и упоминанию того из Девяти Повелителей Ночи, который правил в это время. А между ними были даты, выражавшиеся в бактунах, катунах, тунах и т. д., плюс соответствующие даты по «тцолкину» (260 дней) и «хаабу» (365 дней). На рисунке 10 показана типичная дата, записанная с помощью Длительного счета на «лейденской плите» (или «Лейденской таблице»). Полностью эта дата выглядит так: вводный иероглиф, 8 бактунов, 14 катунов, 3 туна, 1 уинал, 12 кинов, 1 эб, Ояхкин. Кроме системы Длительного счета, Фёрстеман сделал и другие открытия. Изучая Дрезденский кодекс, он показал, что там содержатся «Таблица Венеры» с расчетами движения этой планеты по циклам примерно в 584 дня, а также лунные таблицы для вычисления возможного времени затмений. Может показаться, что он лишь кропотливо изучал древности, имеющие лишь историческое значение, на самом деле это труд гения. Не удивительно, что индейцы оплакивали гибель своих книг, сгоревших в огне по воле невежественных епископов. Они разрушили величайшие научные творения и, в частности, записи астрономических наблюдений за несколько столетий.  Рис. 10. Даты майя с Лейденской плиты Фёрстеман, трудившийся в тиши одной из немецких библиотек, вдали от Центральной Америки, конечно, нашел важнейший ключ к календарной системе майя, хотя и он не решил эту задачу полностью. Научившись читать даты Длинного счета в Дрезденском кодексе, он не мог связать их с датами григорианского календаря. Для этого надо было знать большее число дат, с более точными ссылками и указаниями, чем содержались в памятниках майя. Это суждено было открыть другим исследователям. Предпринимались отдельные попытки фотографировать памятники майя и изучать их, но выполнить это было нелегко — такие памятники находились неблизко один от другого, нередко в труднодоступных местах, в джунглях. Наконец, за дело взялся Альфред Модели, которому и удалось составить довольно полный сборник надписей, который стал теперь достоянием исследователей. Публикация его «Археологии» в приложениях к пятитомнику «Центральноамериканская биология» в 1889 и 1902 годы стала новой важной вехой в изучении культуры майя. Теперь исследователи смогли сопоставить значительное количество надписей с текстом Ланды и с кодексами, известными ранее. Может быть, так и должно было случиться, хотя это вызвало неудовольствие современных исследователей майя: и в этот раз следующий важный шаг сделал человек посторонний. Это был американский предприниматель Джозеф Гудмэн, журналист по профессии. В 23 года он издавал собственную газету в Вирджиния-сити, недалеко от Рено, в штате Невада, под названием «Территорал Энтерпрайз». Вирджиния-сити был беспокойным городом. В тех краях в конце 50-х годов XIX века было найдено золото, и многочисленные любители легкой наживы вскоре превратили Вирджинию в типичный город Дикого Запада. Гудмэн использовал конъюнктуру, не только будучи хозяином местной газеты (где в начале своей карьеры сотрудничал и Марк Твен), он не чурался и дел, связанных с добычей золота. Вскоре он стал богачом и перебрался из края золотой лихорадки в относительно спокойную тогда Калифорнию. Здесь он начал издавать новую газету «Сан-францисканец», купил фруктовый сад в Фресно и посвятил себя новому хобби — изучению майя. В 1897 году он подготовил к публикации первые результаты своих исследований, ставшие частью приложения Модели к его фундаментальной «Центральноамериканской биологии». Игнорируя неравенство Фёрстемана, с ранними работами которого Гудмэн должен был быть знаком, он заявил, что открыл Длительный счет и начальную дату 4 ахау, 8 куму. Современные специалисты по майя, например Эрик Томпсон, убеждены, что у Гудмэна не было достаточно материалов, чтобы самому дойти до этих выводов, что он, должно быть, украл идею у Фёрстемана. Но если даже и так, то Гудмэн внес и свой оригинальный вклад в майянологию. Во-первых, он установил, что у майя были специальные «головные» иероглифы, как альтернатива точкам и черточкам для записи цифр (вроде того, как у нас есть арабские и есть римские цифры). Поэтому при ведении Длительного счета майя пользовались не одной системой. Но гораздо важнее оказалась его публикация 1905 года в газете «Американский антрополог» под заглавием «Даты майя». Именно эта работа оказалась новаторской и позволила связать даты майя с датами в нашем собственном календаре. До сих пор никто из исследователей не мог связать даты в многочисленных надписях майя с григорианской системой. Тщательно изучая книгу Ланды, кодексы и различные центральноамериканские источники, Гудмэн пришел к заключению, которое позволило другим ученым составить единую хронологию истории цивилизации майя. Работу Гудмэна долго игнорировали, но в конце концов на нее обратили внимание, и, с небольшим уточнением в три дня, его хронология теперь принята одним из самых влиятельных специалистов по майя, Эриком Томпсоном[38]. Он установил, что конец предыдущей эпохи, по календарю майя, как и начало нынешней, относится к 13 августа 3114 года до н. э. Так как эпоха майя, по расчетам, должна продолжаться 13 бактунов, или 1 872 000 дней, то конец настоящей эпохи должен наступить 22 декабря 2012 года. В этот последний период нашей эпохи мы и живем. Поделитесь на страничке Следующая глава > history.wikireading.ru Цифры майя — WiKi Цифры майя — запись чисел, основанная на двадцатеричной[1]позиционной системе счисления, использовавшаяся цивилизацией Майя в доколумбовой Мезоамерике. |
Индо-арабская | АрабскаяТамильскаяБирманская | КхмерскаяЛаосскаяМонгольскаяТайская | Восточноазиатские | КитайскаяЯпонскаяСучжоуКорейская | ВьетнамскаяСчётные палочки | Алфавитные | АбджадияАрмянскаяАриабхатаКириллическаяГреческая | ГрузинскаяЭфиопскаяЕврейскаяАкшара-санкхья | Другие | ВавилонскаяЕгипетскаяЭтрусскаяРимскаяДунайская | АттическаяКипуМайяскаяЭгейскаяСимволы КППУ | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | | Нега-позиционная | | Симметричная | |
| Фибоначчиева | |
| Единичная (унарная) |
Эта система использовалась для календарных расчётов и называлась «долгим счётом». В быту майя использовали аддитивную непозиционную систему, сходную с древнеегипетской[2]. Об этой системе дают представление сами цифры майя, которые являются записью первых 19 натуральных чисел в пятеричной непозиционной системе счисления. Аналогичный принцип составных цифр использован в древнейшей известной шестидесятеричной позиционной системе счисления[3] и древнекитайской десятичной позиционной системе для расчётов на счётной доске[4]. Цифры майя состояли из нуля, который обозначался пустой ракушкой, и 19 составных цифр. Эти цифры конструировались из знака единицы (точка) и знака пятёрки (горизонтальная черта). Например, цифра, обозначающая число 19, писалась как четыре точки в горизонтальном ряду над тремя горизонтальными линиями[5]. Сходство конструкции цифр Майя с древнеегипетскими, римскими и древнекитайскими цифрами обусловлено тем, что первоначально расчёты не велись на бумаге. Цифры выкладывались на ровной поверхности специальными палочками. Майя использовали также пустую ракушку и, вероятно, камешки или косточки плодов. Числа свыше 19 Числа свыше 19 писались согласно позиционному принципу снизу вверх по степеням 20. Например: - 32 писалось как (1)(12) = 1 × 20 + 12
- 429 как (1)(1)(9) = 1 × 400 + 1 × 20 + 9
- 4805 как (12)(0)(5) = 12 × 400 + 0 × 20 + 5
Для записи цифр от 1 до 19 иногда также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах. Ноль Позиционная система счисления требует использования нуля для обозначения пустых разрядов. Первая дошедшая до нас дата с нулём (на стеле 2 в Чиапа-де Корсо, Чьяпас) датирована 36 годом до н. э. Первая позиционная система счисления в Евразии, созданная в Вавилоне за 2000 лет до н. э., первоначально нуля не имела, а впоследствии знак нуля использовался только в промежуточных разрядах числа, что приводило к неоднозначной записи чисел. В древнекитайской позиционной системе в промежуточных разрядах вместо нуля использовали пустую клетку счётной доски, а иероглифы для обозначения нуля появились существенно позже. Непозиционные системы счисления древних народов нуля, как правило, не имели[2]. В календаре  Подробное изображение трёх колонок на стеле 1 в Ла-Мохарра. Левая дата — 8.5.16.9.7, то есть 156 год н. э. Подробное изображение трёх колонок на стеле 1 в Ла-Мохарра. Левая дата — 8.5.16.9.7, то есть 156 год н. э. В «долгом счёте» календаря майя была использована разновидность двадцатеричной системы счисления, в которой второй разряд мог содержать только цифры от 0 до 17, после чего к третьему разряду добавлялась единица. Таким образом, единица третьего разряда означала не 400, а 18 × 20 = 360, что близко к числу дней в солнечном году.[источник не указан 119 дней] В истории математики Индейцы Майя относятся к относительно небольшому числу народов, которые самостоятельно создали позиционную систему счисления. Вместе с ними это сумели сделать шумеры, индийцы и китайцы. Древнегреческие астрономы использовали вавилонскую, а точнее шумерскую позиционную систему, благодаря чему мы до сих пор измеряем время и углы в шестидесятеричной системе. Десятичную индийскую позиционную систему европейцы освоили только в средние века с помощью арабов. ПримечанияЛитератураСсылкиСм. такжеru-wiki.org Цифры майя - это... Что такое Цифры майя?Системы счисления в культуре Индо-арабская система счисления | АрабскаяИндийскиеТамильскаяБирманская | КхмерскаяЛаоскаяМонгольскаяТайская | Восточноазиатские системы счисления | КитайскаяЯпонскаяСучжоуКорейская | ВьетнамскаяСчётные палочки | Алфавитные системы счисления | АбджадияАрмянскаяАриабхатаКириллическая | ГреческаяЭфиопскаяЕврейскаяКатапаяди | Другие системы | ВавилонскаяЕгипетскаяЭтрускаяРимская | АттическаяКипуМайская | Позиционные системы счисления | Десятичная система счисления (10) | | 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | | Нега-позиционная система счисления | | Симметричная система счисления | Смешанные системы счисления | Фибоначчиева система счисления | Непозиционные системы счисления | Единичная (унарная) система счисления | | Список систем счисления |
Цифры майя — запись чисел, основанная на двадцатеричной позиционной системе счисления, использовавшаяся цивилизацией Майя в доколумбовой Месоамерике.   Цифры майя Цифры майя Эта система использовалась для календарных расчетов. В быту майя использовали непозиционную систему сходную с древнеегипетской.[1] Об этой системе дают представление сами цифры майя, которые можно трактовать как запись первых 19 натуральных чисел в пятеричной непозиционной системе счисления. Цифры майя состояли из нуля (знак ракушки) и 19 составных цифр. Эти цифры конструировались из знака единицы (точка) и знака пятерки (горизонтальная черта). Например, цифра, обозначающая число 19, писалась как четыре точки в горизонтальном ряду над тремя горизонтальными линиями. Числа свыше 19 Числа свыше 19 писались согласно позиционному принципу снизу вверх по степеням 20. Например: - 32 писалось как (1)(12) = 1×20 + 12
- 429 как (1)(1)(9) = 1×400 + 1×20 + 9
- 4805 как (12)(0)(5) = 12×400 + 0×20 + 5
Для записи цифр от 1 до 19 иногда также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах. Ноль Позиционная система счисления требует использования нуля для обозначения пустых разрядов. Первая дошедшая до нас дата с нулём (на стеле 2 в Чиапа-де Корсо, Чиапас) датирована 36 годом до н. э. Первая позиционная система счисления в Евразии, созданная в древнем Вавилоне за 2000 лет до н. э., нуля не имела, что приводило к неоднозначной записи чисел.[2] В календаре   Подробное изображение трёх колонок на стеле 1 в Ла-Мохарра. Левая дата — 8.5.16.9.7, то есть 156 год н. э. Подробное изображение трёх колонок на стеле 1 в Ла-Мохарра. Левая дата — 8.5.16.9.7, то есть 156 год н. э. В «долгом счёте» календаря майя была использована разновидность 20-ричной системы счисления, в которой второй разряд мог содержать только цифры от 0 до 17, после чего к третьему разряду добавлялась единица. Таким образом, единица третьего разряда означала не 400, а 18×20 = 360, что близко к числу дней в солнечном году. Примечания Ссылки См. также  Цивилизация майя Цивилизация майя Предыстория | Веракрус | Исапа | Ольмеки | Теотиуакан | Эпиольмеки | Города, регионы, государства | Города майя (список) | Баакуль | Мутуль | Кануль | Правители | Пакаль Великий | Текун Уман | Другие персоналии Соперники, соседи, завоевания | Пипили | Тотонаки | Войско, оружие | Военное дело майя | Оружие | Полководцы | Тактика | Общество, семья, экономика | Майяское право | Экономика | Семья | Община | Дороги | Ирригация | Мосты | Торговля | Земледелие | Скотоводство | Керамика | Костюм | Мифология и религия | Мифология майя | Кукулькан | Священный сенот | Сеноты | Священные пещеры майя | 2012 | Язык, письменность | Майяские языки | Письмо майя | Цифры майя | Стелы майя | Надписи на керамике майя | Науки, философия | Философия | Математика | Астрономия | Астрология | Медицина | Календарь | Система координат | Система счёта, мер и весов майя | Культура, искусства, литература | Музыка | Песни | Театр | Поэзия | Литература | Пополь-Вух | Чилам-Балам | Дрезденский кодекс | Кодексы майя | Анналы Какчикелей | Скульптура | Архитектура | Пирамида Кукулькана | Живопись | Ткачество | Настольные игры | Коллективные игры | Месоамериканская игра в мяч | Разное (быт, личности, другое) | Кухня майя | Конкиста и ранний колониальный период Конкистадоры | Педро де Альварадо | Франсиско де Монтехо | Хронисты, историки, лингвисты | Гомара | Диего де Ланда | Когольюдо | Губернаторы | Франсиско де Монтехо | События | Завоевание Мексики | | См. также: Доколумбовы цивилизации | Месоамериканская хронология | Портал: Цивилизация Майя |
dic.academic.ru
|
