"Комбинаторика-это интересно!"-научный проект секция математика. Комбинаторика древней греции

07. Комбинаторика в Древней Греции

Говорить с полной уверенностью об уровНЕ зНАНИй древних греков в области комбинаторики затруднительно, поскольку до нас дошло далеко не все из их научного наследия. В 391 г. Н. Э. толпа монахов разрушила центр языческой науки — александрийский Музеум — и сожгла больШУю часть хранившейся в нем библИОтеки, насчитывавшей многие тысячи томов. Остатки библиотеки разрушались в течеНИе еще трех веков, а в 638 г. н. э. она окончательно погибла при взятии Александрии войсками арабского халифа Омара. Большинство научных книг безвозвратно ПОгибло, и мы можем лишь догадываться об их содержании по кратким пересказам и намекам в сохраНИвшихся рукописях. По этим намекам можно все же судить, что оПРеделеННые представления о комбинаторике у греческих ученыХ Были. Философ Ксенократ, живший в IV в. до н. э., Подсчитывал число слогов. В III в. до н. э. стоик Хрисипп полагал, что число утверждений, получаемых из 10 аксиом, превышает миллион. По мнению же Гиппарха, Из утверждающих аксиом можНО составить 103049 сочетаНИй, а добавив к ним отрицающие, — 310952. Мы не знаем, какой именно смысл придавали эти философы своим утверждениям и как они получали свои результаты — прИВодИМые Гиппархом числа слишком точны, чтобы считать их результатом грубой оценки, и в то же время НЕ поддаются разумНОму истолкованию. По-видимому, у греческих учеНЫх были какие-то не дошедшие до нас правила комбинаторных расчетов, скорее всего ложные. Конкретные комбИнАторные задачИ, касавшиеся перечисленИЯ НЕбольших групп предметов, греки решали без ошибок. Аристотель описал без пропусков все виды ПРавилЬНых трехчленНЫх силлогизмов, а его ученик Аристоксен из Тарента перечислил различные комбинации длинНЫх и коротких слогов в стихотворных размерах. Живший в IV в. н. э. математик Папп рассматривал число пар и троек, которые можно получить пз трех элементов, допуская их повторения. Большое внимание греческие ученые уделяли вопросам, пограничным между комбинаторикой и теорией чисел. Еще в VI в. до н. э. в школе философа-идеалиста и математика Пифагора возникло убеждение, что МИром правят ЧИсла, а вещи только отражение чисел (возможно, что эти идеи возникли у Пифагора под влиянием вавилонской культуры и восходят к еще более древним взглядам шумеров). Поэтому, чтобы познать мир, пифагорейцы начали изучать свойства натуральных чисел. Их исследования о четных и нечетных числах, делимости чисел, простых и составных числах положили основу теории чисел (в науке бывает, что неверные исходные установки дают толчок к полезным исследоваНИям). Как и китайцы, пифагорейцы придавали особое ЗНачение числу 36 — оно было для НИх не только суммой первых 4 четных и первых 4 нечетных чисел, но и суммой первых трех кубов: . Символом совершенства пифагорейцы считали Совершенные числа, равные сумме своих делителей, например, а символом дружбы — Дружественные числа, каждое из которых равно сумме делителей другого числа (например, 220 и 284). Отыскание таких чисел требовало комбинаторного искусства. В школе Пифагора была доказана известная теорема о сторонах прямоугольного треугольника. Это вызвало интерес к представлению чисел в виде суммы двух квадратов, к квадратным числам 1, 4, 9, 16 и т. д. Квадраты натуральных чисел изображались при этом геометрически (рис. 1). Но пифагорейцы рассматривали и иные конфигурации точек, такие, как изображенные на рис. 2 и 3. Каждый треугольник на рис. 2 получается ИЗ ПредыдуЩего Увеличением длины его стороны на 1. Подсчитывая число точек в каждом треугольнике, получаем ПОследовательность треугольных чисел 1, 3, 6, 10 ... Эти числа можно получить, последовательно складывая натуральные числа: 1, 1+2, 1+2+3, 1+2+3+4 и т. Д. Точно так же шестиугольники на рис. 3 приводят к последовательности шестиугольных чисел 1, 6, 15... получаемой при последовательном суммироваНИи арИФметической прогрессии 1+5+9+… В дальнейшем такие суммы удалось выразить с помощью биномиальных коэффициентов , играющих важную роль в комбинаторике. Переход от плоскости к пространству дал возможность строить еще более сложные числа. Например, из треугольников можно составить пирамиды. Подсчитывая число точек в таких пирамидах, пришли к пирамидальным числам 1, 4, 10, 20, ..., которые были суммами ряда 1+3+6+10+ …, составленного из треугольных чисел. Однако дальнейшие обобщеНИя требовали уже введения многомерных пространств, что лежало за рамками возможностей древнегреческой математики. Учение о фигурных числах привлекало к себе математиков на протяжении многих столетий. Ими много занимался живший в XVII в. французский ученый Пьер Ферма, который доказал, например, что любое натуральное число есть или треугольное или сумма 2 или 3 треугольныХ чисел, квадратное или сумма 2, 3 или 4 квадратов, пятиугольное или сумма 2, 3, 4 или 5 пятиугольных и т. д. Как И Многие другие полученные им результаты, он лишь сформулировал это Утверждение в письме к Блэзу Паскалю (юрист по основной профессии, Ферма занимался математикой лишь в часы досуга). Частные случаи этой теоремы доказали Эйлер и Лагранж, а общее доказательство было дано в 1815 г. французским математиком О. Коши. Наряду с комбинаторикой чисел греческие ученые занимались и отдельными вопросами геометрической комбинаторики — правильными и полуправильными многогранниками, составлением фигур из 14 частей особым образом разрезанного квадрата и т. д. Последнему вопросу была посвящена работа Архимеда «Стомахион». < Предыдущая Следующая >

matica.org.ua

История возникновения и развития комбинаторики

Ориентация на общее развитие личности в процессе образования включает элементы истории математики. Использование историко-математического материала на занятиях содействует повышению их общей эффективности. Математика предстает перед студентами не сформировавшейся наукой, а в процессе создания, в динамике. История науки позволяет учащимся увидеть ее движущие силы, наблюдать в действии взаимосвязь и взаимообусловленность научного познания и практической деятельности человека. «Лучший метод для предвидения будущего развития математических наук заключается в изучении истории и нынешнего состояния этих наук» отмечал А.Пуанкаре3.

С этой точки зрения, целесообразно начинать изучение комбинаторики с истории возникновения и развития данной науки.

Прежде, чем та или иная область знания сформируется в особую науку, она проходит длительный период накопления эмпирического материала, период развития в недрах другой, более общей науки, и затем выделяется в самостоятельную науку. Не является исключением и наука про общие законы комбинирования и образования различных конфигураций объектов, получившая название «комбинаторика». Еще в доисторическую эпоху люди столкнулись с проблемой выбора тех или иных объектов, расположения их в определенном порядке, нахождения среди различных расположений подходящих. Например, во время охоты необходимо было выбрать наилучшее расположение охотников, во время битвы – расположение воинов. Они находили свое применение и в часы досуга. «Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие умения рассчитывать, составлять планы и опровергать планы противника. О таких играх английский поэт У. Вордсворт писал:

Среди вещей египетского фараона Тутанхамона, который был захоронен 35 веков назад, в пирамиде, были найдены разграфленные доски, с 3 горизонталями и 10 вертикалями, и фигурки для древней игры «сенет». Ее правила не дошли до наших дней.

В дальнейшем в таких играх, как нарды, шахматы и различных их вариантах (китайские и японские шахматы, японские шашки «го» и т.д.), необходимо было рассматривать различные сочетания передвигаемых фигур. И, как правило, выигрывал тот, кто лучше решал задачи по наиболее удачному расположению фигур.

Вопросы, связанные с комбинаторикой, встречаются в китайских рукописях, относящихся к XIII XII вв. до н.э.5 Китайцы считали, что «все в мире является сочетанием двух начал – мужского и женского, которые обозначались символами ― и −−.». В рукописи «Же Ким» («Книга перестановок») показаны различные соединения этих знаков по два и по три.

«Восемь рисунков из трех рядов символов изображали землю, горы, воду, ветер, грозу, огонь, облака и небо (некоторые рисунки имели и иные значения)». Неудивительно поэтому, что сумма первых 8 натуральных чисел воплощала в представлениях древних китайцев весь мир. Позже были составлены 64 фигуры, содержавшие пять рядов черточек. Видимо, автор рукописи «Же Ким» заметил удвоение числа рисунков при добавлении одного ряда символов. Это можно рассматривать как первый общий результат комбинаторики6.

Из рукописи «Же Ким» мы можем также узнать, что император Ию, который жил примерно 4000 лет назад, «нашел на берегу реки священную черепаху, на ее панцире был изображен рисунок из черных и белых кружков».

Рис. 1

Если заменить каждую фигурку соответствующим числом, возникнет такая таблица:

Рис.2

Если сложить числа в каждой строке, столбце и диагонали, то получится одна и та же сумма 15. В древности китайцы давали мистическое толкование числам. Когда китайцы открыли таблицу с такими чудесными свойствами, то она произвела на них неизгладимое впечатление. Данный рисунок назвали «ло-шу», стали употреблять его при заклинаниях и считать магическим символом. «Магическим квадратом» теперь называют любую квадратную таблицу с одинаковыми суммами по каждой строке, столбце и диагонали.

Комбинаторные задачи, касавшиеся перечисления небольших групп предметов, решали греки. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Арисксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV в. н.э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения.

В XVIII веке происходит расцвет арабской науки. Арабами были переведены многие работы греческих и римских ученых. Арабские алгебраисты, при извлечении корней, вывели формулу для степени суммы двух чисел, которая в истории математики известна нам под названием «бином Ньютона». Историки считают, что эту формулу знал поэт и математик Омар Хайам (XI–XII вв.) Ее в XIII веке приводит в своих трудах Насир ад-Динат-Туси, а в XV веке она была исследована Джемшид ибн Масуд аль-Каши.

Как сообщают нам некоторые европейские источники, восходящие к арабским оригиналам, «коэффициенты этой формулы высчитывали следующим образом: брали число 10001 и возводили его во вторую, третью, четвертую, …, девятую степени»7. Составлялась таблица, имеющая следующий вид:

При опускании в таблице лишних нулей получается треугольная таблица из биномиальных коэффициентов. Арабские ученые знали и основное свойство элементов этой таблицы, выражающееся формулой .

В вычислении биномиальных коэффициентов не отставали от арабов и китайские математики. Уже к XIII веку в книге алгебраиста Чжу Ши-дза «Яшмовое зеркало» приводится таблица таких чисел, вплоть до n=8. Известно также, что «в VIII веке астроном И.Синь вычислил количество различных расположений фигур в игре, которая напоминала шахматы».

Интерес к сочетаниям проявлялся и в Индии. В VII веке индийский математик Бхаскара в книге «Лилавати», изучая проблемы комбинаторики, писал о применении перестановок к подсчету вариаций размера в стихосложении, различных расположений в архитектуре и т. п. В его работе мы можем найти правила для отыскания числа перестановок и сочетаний нескольких предметов. При этом им также рассматривается и случай, когда в перестановках есть повторяющиеся элементы.

В результате развития торговли с Востоком в начале XII века арабская наука проникает в Западную Европу. В то время арабское учебное заведение окончил Леонардо – сын пизанского купца, торговавшего в Алжире. «Он написал книгу «Liber Abaci», которая вышла 1202 году. Леонардо получил прозвище Фибоначчи, он привел в систему всю арифметику арабов», некоторые сведения по геометрии Евклида и добавил к ним результаты своих изысканий. В работе Фибоначчи излагаются новые комбинаторные задачи, например, «об отыскании наименьшего количества гирь, с помощью которых можно получить любой целый вес от 1 до 40 фунтов»8. Леонардо уделял внимание и отысканию целых решений уравнений. Рассмотрение аналогичных задач в последствии привело к появлению количества натуральных решений систем уравнений и неравенств, имеющих право на рассмотрение как на одну из глав комбинаторики. Леонардо выявил новую последовательность, наряду с известными еще со времен греческих математиков, арифметической и геометрической прогрессий, каждый член которых получался по определенным правилам из предыдущих, члены новой последовательности были связаны друг с другом соотношением . Это было первой формулой, где каждый следующий член последовательности выражался через два предыдущих. Подобные формулы получили название рекуррентных (от лат.recurrere – возвращаться). Метод рекуррентных формул оказался впоследствии полезен для решения комбинаторных задач.

Существовавшие еще в глубокой древности азартные игры, получившие особенное распространение после крестовых походов, способствовали развитию комбинаторики.

Наибольшее распространение получила игра в кости – два или три кубика с нанесенными на них очками бросали на стол, и ставку брал тот, у кого выпала большая сумма очков. Несмотря на грозные запреты церкви, азартные игры все же развивались. В любом городе можно было наблюдать картину, которая описана в «Божественной комедии» Данте:

В кости играли еще этруски жители Мохенджо-Даро, это известно из археологических раскопок. Однако, эти древние игры не подвергались математическому исследованию довольно долго.

Позже некоторые игроки, которые наиболее часто играли в кости, подметили, что одни суммы очков выпадают часто, а другие – редко. Были составлены таблицы, показывавшие, сколькими способами можно получить то или иное число очков. Сначала допускалась ошибка – подсчитывали только число различных сочетаний, дававших данную сумму.

Например, при бросании двух костей сумма 6 получается из сочетаний (1, 5), (2, 4), (3, 3), а сумма 7 – из сочетаний (1, 0), (2, 5), (3, 4). Так как три сочетания были различны в обоих случаях, то напрашивался ошибочный вывод о том, что суммы очков 6, 7 и 8 (также получаемая из трех сочетаний костей) должны выпадать одинаково часто. Но согласно опыту 7 очков выпадает чаще. Сочетание (3, 3) при бросании двух костей может быть получено единственным способом, а сочетание (3, 4) – двумя способами. Именно благодаря этому, сумма 7 выпадает наиболее часто. Таким образом, оказалось, что надо учитывать не только сочетание очков, но и их порядок.

Этими вопросами занимались такие известные итальянские математики XVI века, как Д. Кардано, Н. Тарталья и др. Наиболее полно исследовал данный вопрос в XVII веке Галилео Галилей, но его рукопись оставалась неопубликованной до 1718 г.

В 1713 г. была опубликована книга «Искусство предположений» Якоба Бернулли, в которой указывались формулы для числа размещений из элементов по, выводились выражения для степенных сумм и т. д.

Работы Б.Паскаля9 и П.Ферма10 ознаменовали рождение двух новых ветвей математической науки – комбинаторики и теории вероятностей. Ранее комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике или большей частью относились к области математических развлечений. В 1666 году В. Лейбниц11 публикует «Диссертацию о комбинаторном искусстве», в которой впервые появляется термин «комбинаторный». Этот математический труд Лейбница должен был стать лишь началом большой работы, о которой он часто упоминал в своих письмах и печатных трудах. В. Лейбниц планировал для комбинаторики многочисленные приложения: к играм, статистике, к кодированию и декодированию, к теории наблюдений. Он считал, что комбинаторика должна заниматься «одинаковым и различным, похожим и непохожим, абсолютным и относительным расположением, в то время как обычная математика занимается большим и малым, единицей и многим, целым и частью». Иными словами, под комбинаторикой В. Лейбниц понимал примерно то, что мы теперь называем дискретной математикой. К области комбинаторики В. Лейбниц относил и «универсальную характеристику» – математику суждений, то есть прообраз нынешней математической логики. Проекты В. Лейбница казались несбыточными математикам его времени, но сейчас, после создания быстродействующих вычислительных устройств, многие его планы стали претворяться в жизнь, а дискретная математика выросла в своем значении и начала соперничать с математическим анализом.

Замечательные достижения в области комбинаторики принадлежат одному из величайших математиков XVIII века Леонарду Эйлеру12, швейцарцу, прожившему почти всю жизнь в России, где он был членом Петербургской академии наук.

Основная часть научной работы Л. Эйлера посвящена математическому анализу, в котором он проложил новые пути, создал целый ряд новых областей и подвел итоги исследованиям в других областях. Но у Л. Эйлера хватало времени размышлять и над задачами, которые, казалось бы, не заслуживали его внимания,– о том, можно ли обойти мосты в Кенигсберге (ныне Калининграде) так, чтобы не побывать дважды на одном и том же мосту? – можно ли поставить 36 офицеров из 6 разных полков так, чтобы в каждой шеренге и каждой колонне было по одному офицеру каждого воинского звания из каждого полка? – сколькими способами можно разбить данное число на слагаемые и т.д. Работа о мостах явилась зерном, из которого впоследствии выросли топология и теория графов, задача об офицерах оказалась сейчас связанной с планированием экспериментов, а методы, использованные при решении задачи о разбиении чисел, после длительного и сложного пути развития превратились в науку об интегральных преобразованиях, применяемую для решения уравнений математической физики.

После работ Б.Паскаля и П.Ферма, Г.Лейбница и Л.Эйлера можно было уже говорить о комбинаторике как о самостоятельном разделе математики, тесно связанном с другими областями науки, такими, как теория вероятностей, учение о рядах и т.д. Таким образом, комбинаторика как самостоятельная ветвь математики возникла в XVII веке.

На протяжении долгого времени основную роль в изучении мироздания играл математический анализ – дифференциальное и интегральное исчисления, дифференциальные уравнения, уравнения математической физики, вариационное исчисление и т.д. Все процессы рассматривались как непрерывные, чтобы можно было применять к ним развитый аппарат математики непрерывного. С появлением быстродействующих вычислительных машин такие абстрактные области математики, как математическая логика, общая алгебра, стали прикладными. Тогда для составления алгоритмических языков, на которых стали писать программы для машин, понадобились специалисты именно в этих областях математики. Произошло изменение соотношения между дискретной и классической математикой.

Изменилась и роль древнейшей области дискретной математики – комбинаторики. Если раньше комбинаторика применялась для составления занимательных задач, для кодирования и расшифровки древних письменностей, то со временем она превращается в важнейшую область математического знания.

studfiles.net

Комбинаторика — Юнциклопедия

Комбинаторика — раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.

С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлекались составлением магических квадратов (см. Магические и латинские квадраты), в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата, и т. д.

Комбинаторные задачи возникали и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т. д. (Например, задача о расстановке восьми ферзей на шахматной доске так, чтобы ни один из них не оказался под боем, об обходе всех полей доски шахматным конем и т. д. (см. Математика на шахматной доске).

Комбинаторика становится наукой лишь в XVII в. — в период, когда возникла теория вероятностей. Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям. После первых работ, выполненных в XVI в. итальянскими учеными Дж. Кардано, Н. Тартальей и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 г. работу «Об искусстве комбинаторики», в которой впервые появляется сам термин «комбинаторный». Замечательные достижения в области комбинаторики принадлежат Л. Эйлеру. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т. д.

По мере развития комбинаторики выяснилось, что, несмотря на внешнее различие изучаемых ею вопросов, многие из них имеют одно и то же математическое содержание и сводятся к задачам о конечных множествах и их подмножествах. Постепенно выявилось несколько основных типов задач, к которым сводится большинство комбинаторных проблем. Важную область комбинаторики составляет теория перечислений. С её помощью можно подсчитать число решений различных комбинаторных задач. В основе этой теории лежат «правило суммы» и «правило произведения». Они гласят: «если множество $A$ состоит из $m$ элементов, а множество $B$ — из $n$ элементов, причем эти множества не имеют общих элементов, то их объединение $A⋃B$, т. е. совокупность всех элементов из $A$ и $B$, содержит $m+n$ элементов; множество $A×B$, состоящее из всевозможных пар $(a,b)$, где элемент $a$ принадлежит множеству $A$, а элемент $b$ принадлежит множеству $B$, содержит $mn$ элементов».

С помощью правила суммы легко сосчитать и число элементов в $A⋃B$, когда $A$ и $B$ имеют общие элементы. Если обозначить через $A⋂B$ множество всех общих элементов у множеств $A$ и $B$, то оно равно $n(A)+n(B)−n(A⋂B)$, где $n(A)$ — число элементов в множестве $A$. Это утверждение — частный случай так называемой формулы перекрытий.

Часто приходится считать число последовательностей длины $m$, составленных из элементов некоторого множества $A$, состоящего из $n$ элементов, как в случае, когда среди элементов последовательности могут быть повторяющиеся, так и в случае, когда все эти элементы должны быть различными. В первом случае последовательности называют размещениями с повторениями из $n$ элементов по $m$ и их число обозначают $\bar{A}_{n}^{m}$, а во втором — размещениями без повторений, их число обозначают $A_{n}^{m}$. Формулы для $\bar{A}_{n}^{m}$ и $A_{n}^{m}$ таковы:

$\bar{A}_{n}^{m}={{n}^{m}},$ $A_{n}^{m}=n(n−1)\cdot \ldots \cdot (n−m+1).$

Рассмотрим различные размещения без повторений из $n$ элементов по $n$, очевидно, что они отличаются друг от друга лишь порядком элементов; их называют перестановками из $n$ элементов. Число ${{P}_{n}}$ таких перестановок равно $n!$ (см. Факториал):

${{P}_{n}}=A_{n}^{n}=n!.$

Если отвлечься от порядка элементов, то возникает задача: сколько подмножеств, содержащих $m$ элементов и отличающихся одно от другого хотя бы одним элементом, можно извлечь из множества $A$, содержащего $n$ элементов. В комбинаторике такие подмножества называют сочетаниями из $n$ элементов по $m$, их число обозначают $C_{n}^{m}$. Можно доказать, что

$C_{n}^{m}=\frac{n!}{m!\left( n-m \right)!}.$

Целый ряд комбинаторных задач возникает при разбиении множеств на части: найти число таких разбиений, если число частей равно $k$; найти, сколькими способами можно число $n$ записать в виде суммы $k$ слагаемых; найти, сколькими способами можно разложить $n$ предметов по $k$ ящикам, и т. д. Обычно задачи теории разбиений и раскладок сводятся к формуле перекрытий и разобранным выше основным задачам комбинаторики. Такими же способами решаются комбинаторные задачи с ограничениями, например подсчет числа размещений с повторениями, в которых ни один элемент не стоит два раза подряд, и т. д.

В решении комбинаторных задач часто используют графические методы — изображение разбиений числа на слагаемые в виде точечных диаграмм, так называемые графы (геометрические фигуры, состоящие из точек и соединяющих их отрезков) и т. д. Теория графов стала в наши дни одной из наиболее бурно развивающихся частей комбинаторики. Многие общие теоремы этого раздела математики формулируются на языке графов.

Комбинаторика не сводится только к подсчету количества тех или иных подмножеств или последовательностей. При решении комбинаторных проблем иногда нужно лишь доказать, что данная проблема имеет решение, или убедиться в отсутствии его. Например, доказано следующее утверждение: для любых чисел $m$ и $n$ найдется такое число $N$, что любой граф, состоящий из $N$ точек и всех соединяющих эти точки отрезков (они раскрашены в $m$ цветов), содержит часть, состоящую из $n$ точек и соединяющих их отрезков, такую, что все отрезки имеют один и тот же цвет (теорема Рамсея).

Если заданным условиям удовлетворяют несколько конфигураций, т. е. если комбинаторная задача имеет несколько решений, то может возникнуть вопрос о выборе из них решения, оптимального по тем или иным параметрам. Например, если имеется несколько городов, каждые два из которых соединены авиалинией, то возникает задача о том, как путешественнику побывать по одному разу в каждом городе, налетав наименьшее расстояние.

Комбинаторные задачи физики, химии, биологии, экономики и других наук, которые не поддавались ранее решению из‑за трудоемкости вычислений, стали успешно решаться с использованием компьютеров. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники.

В 1970–1980 гг. комбинаторика добилась новых успехов. Например, с помощью компьютера решена проблема четырех красок: доказано, что любую карту можно раскрасить в четыре цвета так, чтобы никакие две страны, имеющие общую границу, не были окрашены в один и тот же цвет.

yunc.org

Методические рекомендации по методике преподавания комбинаторики

Участники проекта: учащиеся 11 класса

Тип проекта: практически-ориентированный

Срок выполнения: 2 недели

Эпиграф урока: «Число, размещения и комбинация – три взаимнопересекающихся, но разных сферы мысли, которыми можно описать все математические идеи». (Д.Д. Сильвестр)

1. Актуальность проекта как учебной технологии.

2. Цель и задания проекта.

Развивать творческое мышление всесторонним анализом проблем, запоминать информацию в виде логических структур, понимать причинно-следственные связи.

3. Механизм реализации проекта.

1. Постановка проблемы.

2. Определение тем и целей проектов.

Проекты можно подавать в форме презентаций или рефератов.

3. Защита проектов.

Тип урока: урок обобщения и систематизации знаний.

4. Оценивание проектов.

2. Просмотр проекта «История возникновения и развития науки комбинаторики».

Комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов - возникла в XVII в. С задачами, в которых приходится выбирать те или иные предметы, размещать их в определенном порядке и отыскивать среди различных размещений лучшие, люди столкнулись еще в доисторическую эпоху, выбирая лучшие размещения охотников во время охоты, воинов во время битвы, инструментов во время работы . Определенным образом располагались украшения на одежде, узоры на керамике. С усложнением производственных и общественных отношений шире приходилось пользоваться общими понятиями о порядке, иерархии, группировке. В том же направлении действовало развитие ремесел торговли. Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда рядом с соревнованиями по бегу, метанию диска, прыжках появились игры, которые нуждались в первую очередь в умении рассчитывать, составлять планы и опровергать планы противника.

Среди предметов, положенных в пирамиду, где 35 веков назад был похоронен египетский фараон Тутанхамон, нашли расчерченную дощечку с тремя горизонталями и 10 вертикалями и фигурки для древней игры «сенет», о правилах которой мы, возможно, никогда не узнаем . Впоследствии появились нарды, шашки и шахматы, а также их различные варианты (китайские и японские шахматы, японские облавные шашки «го» и др.). В каждой из этих игр приходилось рассматривать различные комбинации фигур, имевших способность передвигаться, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышей. Конечно, в этот период никто и не догадывался о науке, которая рассматривает решение комбинаторных задач.

Комбинаторика в Китае

Первое упоминание о вопросах, близких к комбинаторным, встречается в китайских рукописях, относящихся к XII-XIII вв. до н. э. В этих книгах написано, что все в мире является сочетанием двух начал - мужского и женского, которые авторы обозначали символами «инь» и «янь». В рукописи «Же-ким» («Книга перемен») показаны различные соединения этих знаков по два и по три. Восемь рисунков из трех рядов символов отражали землю, горы, воду, ветер, грозу, огонь, облака и небо. Сумма первых 8 натуральных чисел (то есть число 36) воплощала в воображении древних китайцев весь мир. Впоследствии возникла потребность выразить и другие элементы с помощью знаков «инь» и «янь». Были составлены 64 фигуры, состоящие из пяти рядов черточек.

В рукописи «Же-ким» есть и более сложные рисунки. Как утверждает легенда, император Ию, живший примерно 4000 лет назад, увидел на берегу реки священную черепаху, на панцире которой был изображен рисунок из белых и черных кружков. Если заменить каждую фигуру соответствующим числом, появляется такая таблица, где при добавлении чисел в каждой строке, столбике и по диагонали получим одно и то же число 15.

Комбинаторика в Древней Греции

Конкретные комбинаторные задачи, которые касались пересчета небольших групп предметов, греки решали без ошибок. Аристотель описал без пропусков все виды правильных трехчленных силогизмов, а его ученик Аристоксен из Тарента перечислил разнообразные комбинации долгих и кратких слогов в стихотворных размерах. Математик Папп (IV в. Н.э.) рассматривал число пар и троек, которые можно получить из трех элементов.

Наверное, у греческих ученых были какие-то неизвестные нам, правила комбинаторных рассчетов, которые скорее всего были неверными. Схоласт Раймонд Люлли создал в ХVIII ст. машину, которая состояла из нескольких кругов, на которые были нанесены основные предикаты, субъекты, атрибуты и другие понятия схоластической логики. Вращая эти круги, он получал различные совмещения понятий и надеялся получить с их помощью истину.

Комбинаторика в странах Востока

В VIII в. н. э. начался расцвет арабской науки. Арабы перевели много произведений греческих ученых, изучили их, а затем достигли успехов в науке о решении уравнений (само слово «алгебра» - арабского происхождения), теории и практике вычислений. Решая вопрос о нахождении корней любой степени, арабские алгебраисты вывели формулу для степени суммы двух чисел, которая известна под не совсем правильным историческим названием «бином Ньютона». Наверное, именно эту формулу знал поэт и математик Омар Хайям (XI-XII вв. Н.э.).

Работы Паскаля и Ферма дали толчок для рождения двух новых ветвей математической науки - комбинаторики и теории вероятностей. Если до них комбинаторные проблемы затрагивались в общих трудах по астрологии, логике и математике, что в значительной мере считалось математическим развлечением, то уже в 1666 г. Готтфрид Вильгельм Лейбниц публикует «Диссертацию о комбинаторном искусстве», в которой впервые появился термин «комбинаторика». Проекты Лейбница казались невыполнимыми тогдашним математикам, но теперь, после создания ЭВМ, много планов Лейбница начали воплощаться в жизнь, а дискретная математика выросла настолько, что смогла вступить в спор с классическим математическим анализом.

В 1713 г. была опубликована книга «Искусство предположений» Якоба Бернулли, в которой указывались формулы для числа размещений из с n элементов по k, выводились выражение для степенных сумм и т.п. Замечательные достижения в области комбинаторики принадлежат одному из крупнейших математиков XVIII в. Леонарду Эйлеру, швейцарцу, проживший почти всю жизнь в России, где был членом Петербургской академии наук. Основная часть научной работы Эйлера посвящена математическому анализу, в котором он проложил новые пути, создал целый ряд новых областей.

После работ Паскаля и Ферма, Лейбница и Эйлера можно было уже говорить о комбинаторике как об отдельной, самостоятельную ветви математики, тесно связанной с другими областями науки, такими, как теория вероятностей, учение о рядах т.д. В конце XVII в. немецкий ученый Гинденбург и его ученики сделали попытку построить общую теорию комбинаторного анализа. Однако она не имела успеха - в то время еще не было накоплено достаточного количества важных и интересных задач, которые могли бы дать необходимый фундамент для такой теории.

III. Актуализация опорных знаний.

Технология« Продолжите предложение ».

На доске написано задание, учащиеся на выбор учителя подходят ​​и дописывают ответ.

Х={0, 2, 3, 4, 7.} У={2, 4, 7, 9, 14.}

ХпУ =

їиУ =

Х\У =

Технология «Мозаика».

На доске изображена схема. Ученик получает выражения на листах, ему нужно составить правило выбора формулы для решения задач по комбинаторике

4. Просмотр проекта «Интересная комбинаторика».

Ориентировочный опорный конспект проекта

Профессор Отто Лиденброк - главный герой романа Жюля Верна «Путешествие к центру земли», в букинистической лавке попал на манускрипт XIII в., написанный руническим письмом. (Руны - письменные знаки, употреблявшиеся в средневековье и, по легенде, были изобретены самим Одином - верховным богом в исландской мифологии). Но заинтересовала Отто записка, оставленная в этой книге ее бывшим владельцем, знаменитым алхимиком XVII в. Анре Сакнуссемом. Сомнений не было: в записке говорилось о каком-то великом открытии. И хотя запись была сделана хорошо известным профессору руническим письмом, однако прочитать его не удалось. Сообщение было зашифровано. Прочитать его можно было лишь двумя способами: либо рассмотреть все варианты размещения 20 рунических знаков, или найти ключ к шифру. Как вы думаете, каким способом Отто Лиденброк прочитал записку?

Его ассистент Аксель подсчитал, что переставлять рунические знаки профессору пришлось бы 2 32 902 008 176 640 000 раз. (В. А. Тадеев «Неформальная математика» Тернополь, 2003).Комбинаторика позволила прочитать и крито-микенское линейное письмо. Первые надежные основы расшифровки этой письменности заложила Алиса Д. Кобер, которая защитила в 1932 г. докторскую диссертацию по математике в Колумбийском университете. Рядом с исследованиями по чистой математике, она много усилий приложила к расшифровке древних письменностей. Изучив знаки критского письма, Алиса установила, что это письмо состоит из складов. Кобер получила координатную сетку, в которой вместо осей координат стояли номера гласных и согласных букв. В этой сети был только один недостаток - никто не знал, какие именно гласные и согласные формируют эту систему координат. Лишь через два года после смерти исследовательницы молодой английский архитектор Майкл Вентрис, расширяя ее координатную сетку, попытался угадать значение некоторых гласных (число гласных меньше числа согласных). Одна из попыток закончилась удачно - текст заговорил на языке, напоминающем греческий. Но это не был классический греческий язык «Илиады» и «Одиссеи», а греческий язык более ранней эпохи. Вентрису помог завершить расшифровку выдающийся знаток раннего греческого языка Чедвик. Используя имена царей и списки географических названий, исследователи расшифровывали один состав за другим. А потом началась быстрая расшифровка - три десятка знаков получили свое значение. Это был полный триумф комбинаторного подхода.

Не только азартные игры побудили математиков к комбинаторным размышлениям. Еще с древних времен дипломаты, практиковали тайную переписку, изобретали все более сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Одним из простейших шифров была «тарабарская грамота», в которой буквы заменялись другими по определенным правилам. Однако такие шифры легко разгадывались по характерным сочетаниям букв. Поэтому стали применять шифры, основанные на комбинаторных методах, например, на разных перестановках букв, замена букв с использованием ключевых слов и т.д. Для кодирования и расшифровки привлекались математики. Еще в конце XVI в. расшифровкой переписки между врагами французского короля Генриха III с испанцами занимался один из создателей современной алгебры Франсуа Виет. А в Англии XVII в. монархические заговорщики удивлялись скорости, с которой Кромвель разгадывал их задумы. Монархисты считали шифры, которыми они пользовались в переписке, нерасшифрованными, и считали, что ключи к ним были выданы кем-то из участников мятежа. И только после падения республики и царствования Карла II они узнали, что все их шифры разгадывал один из лучших английских математиков того времени, профессор Оксфордского университета Уоллис, который имел исключительный комбинаторный талант. Он назвал себя основателем новой науки «криптографии». Шифрами пользовались не только дипломаты и мятежники, но и сами ученые. До 17 в. Почти не существовало научных журналов. Ученые узнавали о достижениях своих коллег из книг или частных писем. Это создавало большие трудности при опубликовании новых результатов - ведь издание книг занимало годы, а написать о своих открытиях в письме было рискованно – кто-нибудь мог присвоить изобретение. Поэтому между учеными часто возникали споры на тему преимуществ. Еще в конце XVII в. шли долгие споры.

В древности Архимеду приходилось хитрить. Когда некоторые александрийские ученые присваивали себе его результаты, описанные в письмах, он писал им еще одно письмо, состоящее из формул для вычислений объемов и площадей различных фигур и тел. Ученые утверждали, что эти формулы им давно известны и ничего нового Архимед им не сообщил. Но тут выяснялось, что все эти формулы неверны. Для того, чтобы обеспечить приоритет и не допустить преждевременной огласки полученных результатов, ученые в краткой форме формулировали суть открытия, а потом переставляли буквы и отправляли письма с переставленными буквами своим коллегам. Такие тексты с переставленными буквами назывались анаграммами. Навыки в разгадке сложных шифров помогли ученым, когда археологи начали находить камни и черепа с тайными знаками. Одним из крупнейших успехов в расшифровке было прочтение французским филологом Жаном Франсуа Шамполем иероглифов, которыми писали египтяне еще до того, как возникла наука у древних греков. Технология «Лото».

На доске лист бумаги с ответами. Учащимся раздают на листах задачи с операциями над, соединениями, которые написаны с одной стороны листа и с элементами рисунка с другой стороны. Решив задачу, ученик наклеивает свой ​​элемент рисунка на место, где написан его ответ. В результате школьники получают полный рисунок, который свидетельствует о правильном решении задачи.

а)

б)

в)

г)

д)

е) Просмотр проекта «Применение комбинаторики».

Ориентировочный опорный конспект проекта

Комбинаторика - важный раздел математики, знание которого необходимо работникам различных специальностей. С комбинаторными задачами приходится иметь дело физикам, химикам, биологам, лингвистам, специалистам по кодам и т.п.. Комбинаторные методы лежат в основе решения многих задач теории вероятностей и ее приложений.

Комбинаторика в биологии

Сложность строения биологических систем, их строгая иерархичность, взаимосоединение отдельных процессов в целом организме делают биологию пригодной для применения комбинаторных методов. Советский биолог А. А. Любищев предполагал даже, что схожесть растений и морозных узоров на окнах не случайна - в обоих случаях проявляются определенные законы комбинирования частей в одно целое. Когда биологи начали изучать передачу генетической информации у бактерий, то заметили, что в процессе этой передачи хромосомы переходят от одной бактерии к другой не полностью. Они надеялись, изучая части которые перешли из одной бактерии к другой, определить порядок размещения генов в хромосоме. Но карты хромосом, составленные в разных лабораториях, были непохожимы друг на друга. Однако, детально сравнив полученные карты, французские ученые

Одной из наиболее сложных загадок в биологии XX в. было строение «нитей жизни» - молекул белка и нуклеиновых кислот. Оказалось, что молекулы белка - это объединение нескольких длинных цепей, состоявших из 20 аминокислот. Сочетая комбинаторные разбирательства с изучением рентгеновских снимков, ученым удалось разгадать строение многих белков, в том числе гемоглобина, инсулина и т.д. Достижением комбинаторного подхода к проявлениям жизни можно считать расшифровку строения дезоксерибонуклеиновой кислоты (ДНК), сделанную в Кембридже Ф. Криком и Дж. Уотсоном в 1953 г.

Комбинаторика в химии

17 февраля 1869 из хаоса химических элементов, каждый из которых имел свои свойства, возникла таблица - был открыт периодический закон. Это открытие было сделано Дмитрием Ивановичем Менделеевым, профессором Петербургского университета. Готовя курс лекций по общей химии, он задумался над порядком, в котором нужно было рассказывать об элементах. Как писал впоследствии сам ученый, «искать что-то, хотя бы грибы, или какую-то зависимость, можно, как смотря и пробуя». Для того, чтобы «смотреть и пробовать», он начал подбирать, написав на отдельных карточках, названия элементов с их атомными массами и свойствами данного элемента, похожие элементы и атомные массы. Раскладывая свой ​​химический пасьянс, великий ученый после напряженных раздумий нашел правильное размещение элементов. Говорят, что конечный вид таблицы предстал перед ним во сне, когда, утомленный непрерывной работой над ней, он прилег отдохнуть. Поражает, что открытие было сделано Менделеевым за один день - утром 17 февраля 1869 он еще и не начинал раскладывать свой ​​пасьянс, а к вечеру того же дня таблица была готова.

В физике комбинаторика является необходимой при изучении особенностей кристаллов, описания модели ферромагнетизма т.д..

Комбинаторика эпохи компьютеров

В нашу эпоху комбинаторика из области, которая интересовала прежде всего лишь отдельных авторов задач и находила применение в кодировке и расшифровке древних письменностей, превратилась в область, находящуюся на магистральном пути развития науки. Шифрование, кодирование, дешифрование письменной информации - важное, но не единственное применение комбинаторики. Кодами являются также государственные номерные знаки, штрих-коды. Целенаправленный выбор «разных возможных вариантов» необходим для составления расписания движения транспорта, расписания занятий в школе, а еще как аппарат для решения задач теории вероятности.

Проверка умений и навыков решения решать задачи по данной теме.

Самостоятельная работа (5 мин).

Учитель раздает задачи на листах. 1 вариант - ученик выбирает и решает только задачу на размещение, 2 вариант - ученик выбирает и решает только задачу на комбинацию.

1 вариант

1. В группе есть 10 человек. Сколькими способами можно выбрать 5 из них для экскурсии?

2. Сколькими способами можно выбрать старосту и заместителя, если в классе 25 учеников?

3. Сколькими способами можно построить шеренгу из 5 человек.

2 вариант

1. Сколькими способами можно расставить 6 стульев вокруг стола?

2. Сколькими способами можно выбрать инструктора и старшего инструктора из 30 человек?

3. Сколькими способами можно выбрать 2 дежурных из 25 человекч. 1 ч. 2

ansya.ru

Реферат по математике по теме: "Комбинаторика"

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ

ГОРОДА

МОСКВЫ

«КОЛЛЕДЖ ПОЛИЦИИ»

Реферат по дисциплине Математика

На тему: «История развития комбинаторики и её роль в различных сферах человеческой деятельности».

Выполнила

Курсант 15 взвода

Алехнович В.А.

Преподаватель

Зайцева О.Н.

Москва

2015

Содержание:

и развития комбинаторики и теории вероятностей…... 3

• Области применения комбинаторики…………………. 11

• Вывод……………………………………………………. 15

• Ссылки…………………………………………………... 16

Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).

До того, как та или иная область знания формируется в особую науку, она сначала проходит длительный период накопления эмпирического материала, потом развивается в недрах другой, более общей науки и лишь затем выделяется в самостоятельную ветвь. С задачами, в которых приходится выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшие расположения охотников во время охоты, воинов во время битвы, инструментов во время работы. Определенным образом располагались украшения на одежде, узоры на керамике, перья в оперении стрелы. Ещё в древности было замечено, что имеются явления, обладающие следующей особенностью: при малом числе наблюдений над ними не замечается никакой зависимости, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. Наши предки понимали, что у десятка охотников вероятность поразить животное на охоте больше, чем у одного; вероятность благополучно переправиться на противоположный берег реки через брод выше, чем в глубоководном ее месте и т.д. Позднее, на основе наблюдения и опыта, человек стал оценивать случайные события, классифицировать их исходы как невозможные, возможные и достоверные. Он заметил, что случайностями не так уж редко управляют объективные закономерности.

По мере усложнения производственных и общественных отношений все чаще приходилось пользоваться понятиями о порядке, иерархии, группировании.

В пирамиде, где был похоронен египетский фараон Тутанхамон, нашли разграфленную доску с тремя горизонталями и 10 вертикалями и фигурки для древней игры ''сенет'', правило которой мы, вероятно, никогда не узнаем. Позже появились нарды, шашки и шахматы, а также их различные варианты (китайские и японские шахматы, японские облавные шашки ''го'' и т. д.). В каждой из этих игр приходилось рассматривать различные сочетания передвигаемых фигур, и выигрывал тот, кто их лучше заучил.

В китайских рукописях, относящихся к XII-XIII вв. до н.э. встречаются упоминания о вопросах, близких к комбинаторным (точно датировать эти рукописи невозможно, поскольку в 213 г. до н.э. император Цинн Ши-Хуан приказал сжечь все книги, так что до нас дошли сделанные позднее копии). В этих книгах писалось, что все в мире является сочетанием двух начал – мужского и женского, которое авторы обозначали символами -- и ----. В рукописи ''Же Ким'' (''Книга перестановок'') показаны различные соединения этих знаков по два и по три.

Восемь рисунков из трех рядов символов изображали землю, горы, воду, ветер, грозу, огонь, облака и небо (некоторые рисунки имели и иные значения). Неудивительно поэтому, что сумма первых 8 натуральных чисел (т. е. число 36) воплощала в представлениях древних китайцев весь мир.

Понадобилось выразить по мере углубления знаний и другие элементы мироздания с помощью тех же знаков -- и -- --. Были составлены 64 фигуры, содержавшие уже пять рядов черточек. Надо полагать, что автор рукописи ''Же Ким'' заметил удвоенные числа рисунков при добавлении одного ряда символов. Это можно рассматривать как первый общий результат комбинаторики.

В 391 г. н. э. толпа монахов разрушила центр языческой науки александрийский Музеум – и сожгла большую часть хранившейся в нем библиотеки, насчитывавшей многие тысячи томов. Остатки библиотеки разрушались в течение еще трех веков, а в 638 г. н.э. она окончательно погибла при взятии Александрии войсками арабского халифа Омара, и поэтому большинство научных книг безвозвратно погибло, и мы можем лишь догадываться об их содержании по кратким пересказам и намекам в сохранившихся рукописях. По этим намекам можно все же судить, что определенные представления о комбинаторике у греческих ученых были. Философ Ксенократ, живший в IV в. до н.э., подсчитывал число слогов. В III в. до н.э. историк Хрисии полагал, что число утверждений, получаемых из 10 аксиом, превышает миллион. По мнению же Гиппарха, из утверждающих аксиом можно составить 103 049 сочетаний, а добавив к ним отрицающие, 310 952. Мы не знаем, какой именно смысл придавали эти философы своим утверждениям и как они получали свои результаты – приводимые Гиппархом результаты слишком точны, чтобы считать их результатом грубой оценки, и в то же время не поддаются разумному истолкованию. По-видимому, у греческих ученых были какие-то, не дошедшие до нас правила комбинаторных расчетов – скорее всего ложные.

Конкретные комбинаторные задачи, касавшиеся перечисления небольших групп предметов, греки решали без ошибок. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Арисксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV в. н.э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения.

Греческие ученые уделяли большое внимание вопросам, пограничным между комбинаторикой и теорией чисел. Еще в VI в. до н.э. в школе философа-идеалиста математика Пифагора возникло убеждение, что миром правят числа, а вещи только отражение чисел. Пифагорейцы начали изучать свойства натуральных чисел. Их исследования о четных и нечетных числах, делимости чисел, простых и составных числах положили основу теории чисел. Как и китайцы, пифагорейцы придавали особое внимание числу 36 – оно было для них не только суммой первых 4 четных и первых 4 нечетных чисел, но и суммой первых трех кубов: 36 = . Символом совершенства пифагорейцы считали совершенные числа, равные сумме своих делителей, например, 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14, а символом дружбы – дружественные числа, каждое из которых равно сумме делителей другого (например, 220 и 284). Отыскание таких чисел требовало комбинаторного искусства.

Доказательство известной теоремы о сторонах прямоугольного треугольника вызвало интерес к представлению чисел в виде суммы двух квадратов, к квадратным числам 1, 4, 0, 10 и т. д. Квадраты натуральных чисел изображались при этом геометрически. Пифагорейцы рассматривали и иные конфигурации точек, такие, как изображены на рисунке (рисунок). Каждый треугольник на рисунке получается из предыдущего увеличением длины его стороны на 1. Подсчитывая число точек в каждом треугольнике, получаем последовательность треугольных чисел: 1, 3, 6, 10 …. Эти числа можно получить, последовательно складывая натуральные числа. Точно так же шестиугольники приводят к последовательности шестиугольных чисел 1, 0, 15… получаемой при последовательном суммировании арифметической прогрессии 1+ 5+ 9+ … В дальнейшем такие суммы удалось выразить с помощью биноминальных коэффициентов, играющих важную роль в комбинаторике.

Магические тайны учения и обряды возникли среди фанатичных иудаистов - сторонников колдовства и магии, проповедовавших культ единого бога. Библия была провозглашена собранием божественных откровений, где каждому слову и числу придавалось особое мистическое значение. В каббалистических вычислениях евреев распространено изучение священных текстов и отдельных слов заменой букв числами. Для латинской азбуки: a = 1, b = 2 c = 3, d = 4… В имени богослова Johanes Huss (Иоганн Гусс)после такой замены букв числами получалась общая сумма «очков», равная 145. На эту сумму надо было подобрать другие слова, отражающие внутреннюю духовную сущность человека. Это магическое действие в каббалистике называется гематрией. Задача не из простых, на поиск таких бесплодных решений нередко тратились годы, а то и жизнь. В нашем примере имени Иоганн Гусс соответствуют слова: sermo domini dei и суммы цифр: 18+ 5+ 17+ 12+ 14 = 66; 4+ 14+ 12+ 9+ 13+ 9 = 61; 4+ 5+ 9 = 18, что в целом равно 145 и в точности соответствует исходной сумме очков. В переводе три латинских слова означают: ''Слово Господа Бога''. Итак, получилось: ''Иоганн Гусс = слово Господа Бога'' – смысл найден.

Упадок науки в эллинистических странах, отражавший общий кризис рабовладельческого общества, начинается со II в. до н.э. Многие работы того времени были посвящены мистическим толкованиям чисел в духе пифагорейцев (например, ''Арифметическая теология'' неопифагорейца Никомаха, жившего в I-II вв. н.э.). Большое развитие получили различные числовые суеверия и толкования, связанные с заменой букв соответствующими числами (греки обозначали числа с помощью букв – первые 9 букв алфавита обозначали числа от 1 до 9, следующие за ними – от 10 до 90, а последние 9 букв – от 100 до 900). Были ''ученые'', называвшиеся каббалистами, которые подвергали такому ''анализу'' слова Библии и других священных книг и делали на основе своих изысканий пророчества о будущем мира.

Не чуждался каббалистических вычислений и известный немецкий математик, монах ордена св. Августина Михаэль Штифель (1468 – 1567). Он применил каббалистику к имени тогдашнего папы римского Льва X, спекулировавшего индульгенциями, и сделал поразительное открытие: католический папа и есть апокалипсический зверь, ведь его имени соответствует число 666. Поисками смысла, заключенного в числе 666, занимался и Исаак Ньютон (1643 – 1727), в конце своей жизни написавший сочинение о пророке Данииле. Мания числа 666 веками использовалась не только для идеологической борьбы с неугодными людьми, но и в борьбе целых религиозных течений.

В Россию числовая мистика проникла из Византии. Православное духовенство неоднократно запрещало сочинения по астрономии и геометрии, не делая строгого различия между действительными и ложными знаниями. Тем не менее тайные науки продолжали существовать, о чем можно судить по широко распространенному в народе взгляду на Петра I как на Антихриста – его число тоже 666.

Астрологи также занимались комбинаторикой. Их интересовал вопрос о движении планет и их влиянии на судьбы людей. Особое значение придавали они сочетаниям планет – встречам различных планет в одном знаке зодиака. Астролог Бен Эзра в 1140 г. рассчитал количество сочетаний семи планет по две, по три и т. д. Он знал, что число сочетаний планет по три равно числу сочетаний по четыре. В окончательном виде формулу для числа сочетаний получил живший в XIV веке Л. Гершон, доказавший, что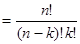

Эту формулу в начале XVII в. вывел французский математик П. Эригон.

Комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике, а большей частью относились к области математических развлечений, то уже в 1666 г. Г. В. Лейбниц публикует ''Диссертацию о комбинаторном искусстве'', в которой впервые появляется сам термин ''комбинаторный''. Титульный лист книги двадцатилетнего автора, имевшего уже ученую степень бакалавра… юриспруденции, обещал приложения ко всем областям науки и новый подход к логике изобретения, а тематика введения могла соперничать по своей широте с программой, которую, как свидетельствует Льюис Кэрролл, наметил Плотник для бесед с устрицами. Там провозглашалось приложение теории к замкам, органам, силлогизмам, смешению цветов и стихосложению, к логике, геометрии, военному искусству, грамматике, юриспруденции, медицине и теологии.

Диссертация Г.В.Лейбница должна была стать лишь началом большой работы, о которой он часто упоминал в своих письмах и печатных трудах и для которой делал в своих записных книжках многочисленные заметки. Из них видно, что Лейбниц планировал для комбинаторики все новые и новые приложения: к кодированию и декодированию, играм, статистике, теории наблюдений. Он считал, что комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным расположением, в то время как обычная математика занимается большим и малым, единицей и многим, целым и частью. Иными словами, под комбинаторикой Лейбниц понимал примерно то, что мы теперь называем дискретной математикой. К области комбинаторики Г.В.Лейбниц относил и ''универсальную характеристику'' – математику суждений, т. е. прообраз нынешней математической логики.

Проекты Г.В.Лейбница казались несбыточными здравомыслящим математикам его времени, но сейчас, после создания быстродействующих вычислительных устройств, многие планы Г.В.Лейбница стали претворяться в жизнь, а дискретная математика выросла в своем значении настолько, что начала соперничать с классическим математическим анализом.

В 1713 г. была опубликована книга ''Искусство предположений'' Якоба Бернулли, в которой указывались формулы для числа размещений из n элементов по k, выводились выражения для степенных сумм и т. д.

Таким образом, как наука теория вероятностей зародилась в XVII в. «Математика случая» − так назвал теорию вероятностей один из ее основателей французский ученый Б.Паскаль. Возникновение понятия «вероятности» было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с развитием азартных игр, популярных в ту пору среди знати, феодалов и дворян. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова «hazard», означающего «случай», «риск». Азартными называют те игры, в которых выигрыш зависит не только и не столько от умения игрока, но и от случайности. Особенно распространенной была игра в кости. Было замечено, что при многократном бросании однородного кубика (все шесть граней которого отмечены соответственно числами 1, 2, 3, 4, 5, 6) число очков от 1 до 6 выпадают в среднем одинаково часто, иными словами, выражаясь языком математики, выпадение определённого числа очков имеет вероятность, равную 1/6. Аналогично вероятность появления на верхней грани кости чётного числа очков равна 3/6, так как из шести равновозможных случаев чётное число появляется только в трёх.

Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных - алгебраиста Д. Кардана (1501 − 1576) и Г. Галилея (1564 − 1642). Однако открытие этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым − Блезу Паскалю (1623 − 1662) и Пьеру Ферма(1601 − 1665).

Один из представителей французской знати того времени, страстный игрок де Мере написал Б.Паскалю письмо, в котором просил ответить на ряд вопросов. Денежный выигрыш при игре в кости обычно зависит от комбинации выпавших чисел, на которую делаются ставки. Одна из таких комбинаций − выпадение хотя бы одной шестёрки при четырёх бросаниях игральной кости. Де Мере смог подсчитать число шансов этой комбинации. Более сложные комбинации возникали, если бросали сразу две кости. Де Мере пытался определить, сколько раз надо бросить пару костей, чтобы вероятность хотя бы одного появления двух шестёрок была больше 1/2. Он подсчитал, что достаточно 24 бросаний. Однако опыт игрока заставил де Мере сомневаться в правильности своих вычислений. Тогда он и обратился с этой задачей к математику Б.Паскалю, который предложил правильное решение. Эта задача кавалера де Мере заставила Б.Паскаля заняться изучением случайных событий. А в переписке Б.Паскаля и П.Ферма впервые стали упоминаться понятия теории вероятностей.

Подсчёт всех возможных и благоприятствующих данному событию случаев нередко представляет большие трудности. Вот почему для решения таких задач некоторые игроки обращались к крупным учёным. Х.Гюйгенсу был задан такой вопрос: «Если бросить одновременно три игральных кости, то какая сумма очков будет выпадать чаще − 11 или 12?» Подсчёт всех различных случаев здесь прост: N=63=216, но сумма 11 может получиться следующими шестью различными способами: 1+4+6, 1+5+5, 2+3+6, 2+4+5, 3+3+5, 3+4+4. Также шестью различными способами образуется сумма 12: 1+5+6, 2+4+6, 2+5+5, 3+3+6, 3+4+5, 4+4+4. Это обстоятельство наводит на мысль, что обе суммы должны появляться одинаково часто. Однако это не так. Было замечено, что сумма 11 появляется чаще суммы 12. Дело в том, что вышеуказанные суммы по три числа сами по себе неодинаково часто выпадают. Так, если каждую из трех костей окрасить по-разному, скажем, в белый, красный и зелёный цвет, то становится ясным, что сочетание, в котором имеются три различных слагаемых, например (1+4+6), может получаться шестью различными способами:

1) 1 бел. + 4 красн. + 6 зел.; 2) 1 бел. + 6 красн. + 4 зел.;

3) 4 бел. + 1 красн. + 6 зел.; 4) 4 бел. + 6 красн. + 1 зел.;

5) 6 бел. + 1 красн. + 4 зел.; 6) 6 бел. + 4 красн. + 1 зел.

Аналогично сочетание с двумя одинаковыми слагаемыми, например (2+5+5), может получиться тремя различными способами, в то время как сочетания с одинаковыми слагаемыми, вроде (4+4+4), получается единственным способом. И вот для 11 очков мы получим, таким образом, не шесть различных способов, а 1×6 + 1×3 + 1×6 + 1×6 + 1×3 + 1×3 = 27. Аналогично, для суммы же 12 число различных способов будет равно 25.

Решение порой довольно сложных задач, с которыми обращались заинтересованные лица к Б.Паскалю, П.Ферма, Х.Гюйгенсу, способствовало разработке основных понятий и общих принципов теории вероятностей. Азартные игры стали для ученых удобной моделью для решения задач и анализа понятий данной теории. Об этом говорил ещё Х.Гюйгенс в своей книге «De ratiociniis ludo alleae» («О расчётах в азартной игре», 1657), которая была первой книгой в мире по теории вероятностей. Он писал: «При внимательном изучении предмета читатель заметит, что он занимается не только игрой, а что здесь даются основы глубокой и весьма интересной науки». Х.Гюйгенс впервые ввёл важное для теории вероятностей понятие математического ожидания, которое получило дальнейшее развитие в трудах Д. Бернулли, Даламбера и др. На развитие теории вероятностей оказали серьёзное влияние потребности науки и запросы практики, в первую очередь страховое дело, начатое в некоторых странах ещё в XVI в.

Таким образом, в 60-е годы XVII в. были выработаны первые понятия и некоторые элементы теории вероятностей.

Следующий этап истории теории вероятностей (XVIII − начало XIX вв.) связан, главным образом, с именами французских математиков А.Муавром (1667 − 1754), П.Лапласом (1749 − 1827), С.Пуассоном (1781 − 1840) и А.Лежандром (1752 − 1833) и немецкого математика К.Гаусса (1777 − 1855). «Аналитическая теория вероятностей» П.Лапласа считается классическим трудом по данному разделу математики. В это время в теории вероятностей, кроме понятия случайного события, рассматривается и понятие случайной величины. Теория вероятностей начала применяться в теории ошибок измерений, теории стрельбы и т.п.

В конце XVIII в. немецкий ученый Гинденбург и его ученики сделали даже попытку построить общую теорию комбинаторного анализа. Однако она не увенчалась успехом – в то время еще не было накоплено достаточного количества важных и интересных задач, которые могли бы дать необходимый фундамент для такой теории.

В середине XIX в. преподаватель Высшей реальной школы города Брюнн Г.И.Мендель производил опыты с горохом, в результате которых были открыты законы наследственности. Ученый скрестил два сорта гороха с жёлтыми и зелёными семенами, после чего растения дали только желтые семена (первое поколение гибридов). После самоопыления растений, выращенных из этих семян (второе поколение гибридов), появился горох и с жёлтыми, и с зелёными семенами. Мендель подсчитал, что отношение числа растений с жёлтыми семенами к числу растений с зелеными семенами равно 3,01. Механизм наследования так же случаен, как и исход бросания монеты или игральной кости.

В ХХ веке произошло строгое логическое обоснование теории вероятностей советским математиком А.Н.Колмогоровым.

Современный период истории теории вероятностей характеризуется возникновением и развитием многих новых областей и направлений. Наряду с понятием случайного события и случайной величины рассматриваются и играют наиболее существенную роль понятия случайной функции и случайного процесса. Круг применения теории вероятностей в различных областях науки и техники расширился настолько, что сейчас ее по праву можно считать одной из наиболее прикладных частей математики. Методы теории вероятностей широко применяются в различных отраслях техники и естествознания: в теории надёжности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках.

Теория вероятностей служит также для обоснования математической и прикладной статистики, которая используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приёмочном контроле качества продукции и для многого другого.

Комбинаторика это большой и важный раздел математики, изучающий множества целых чисел и перестановки внутри этих множеств. Комбинаторика имеет огромное значение для многих сфер человеческой деятельности.

Многие специалисты в области математики и физики считают, что именно комбинаторная задача может стать толчком в развитии всех технических наук. Достаточно лишь нестандартно подойти к решению тех или иных проблем, и тогда можно будет ответить на вопросы, которые уже несколько веков не дают покоя ученым. Некоторые из них всерьез утверждают, что комбинаторика является подспорьем для всех современных наук, особенно космонавтики. Намного проще будет высчитывать траектории полета кораблей с помощью комбинаторных задач, также они позволят определить точное нахождение тех или иных небесных светил. Реализация нестандартного подхода уже давно началась в азиатских странах, там ученики даже элементарные задачи по умножению, вычитанию, сложению и делению решают, используя комбинаторные методы. На удивление многих европейских ученых, методика действительно работает. Школы Европы пока что только начали перенимать опыт своих коллег. Когда именно комбинаторика станет одним из основных разделов математики, предположить сложно. Сейчас наука изучается ведущими учеными планеты, которые стремятся популяризировать ее.

Ссылки:

http://www.edubrilliant.ru/brigens-345-1.html

http://e-science.ru/node/106887

http://yandex.ru/clck

http://fb.ru/article/149409/kombinatornaya-zadacha-prosteyshie-kombinatornyie-zadachi-kombinatornyie-zadachi-primeryi

infourok.ru

"Комбинаторика-это интересно!"-научный проект секция математика

Оглавление

Введение

стр. 2

1.

Понятие комбинаторики.

стр. 4

2.

История развития комбинаторики.

стр. 5

2.1

Дерево возможных вариантов

стр. 6

2.2

Перестановки.

стр. 9

2.3

Размещение.

стр. 10

3.

Комбинаторика в различных областях жизнедеятельности человека.

стр. 13

3.1

Комбинаторика в литературе

стр. 13

3.2

Комбинаторика на шахматной доске и в играх

стр. 15

3.3

Комбинаторика и кубик Рубика

стр. 16

3.4

Старинные задачи

стр. 17

Заключение

стр. 18

Литература

стр. 19

Приложение

стр. 21

В практической деятельности человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. С комбинаторными вычислениями приходится иметь дело представителям многих специальностей: прорабу при распределении между рабочими различных видов работ, диспетчеру при составлении графика движения. Завуч школы, составляя расписание учебных занятий, использует разные комбинации, шахматист из различных комбинаций выбирает наилучшую и т.д.

Современная жизнь делает задачи на комбинаторные вычисления актуальными, так как появление компьютеров резко увеличило возможности комбинаторики и расширило сферу ее применения.

Прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни. Интерес к теме возник, когда я участвовала в олимпиаде по математике, и там встречались следующие задачи:

Задача 1. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько, туристов не владеют ни одним языком?

Задача 2. Бег с препятствиями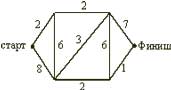

На дорожках стадиона расставлены барьеры (число барьеров на каждой дорожке указано на рисунке). Кенгуру хочет пробежать от старта до финиша, перепрыгивая через наименьшее возможное число барьеров. Сколько раз Кенгуру придется перепрыгнуть через барьеры?

(A)11; (B) 8; (C) 10; (D) 18; (E) 6;

После олимпиады, я задал учителю математики вопрос: «Как можно удобным способом решить задачи такого типа?» И, после этого узнал, что есть раздел математики - «Комбинаторика».

Зная комбинаторику, мы сможем найти ответы на многие интересные вопросы: сколько существует трёхзначных чисел, сколькими способами в футбольной команде можно выбрать капитана и его заместителя, сколькими способами 8 человек могут встать в очередь к театральной кассе, сколько существует семи значных чисел, не содержащих цифры 5 и, наконец, какова вероятность выиграть в русское лото. Очень интересно! Неужели и я - смогу это понять?

Так появился этот проект. Желание ответить на эти вопросы и определило цель моего проекта.

Цель проекта: научиться решать задачи из раздела «комбинаторика».

Для достижения цели были поставлены следующие задачи:

1. Изучить исторический и теоретический материал о комбинаторике.

2. Систематизировать задачи на комбинаторику по типам решения.

3. Выяснить, какие задачи в жизни приходится решать людям.

При работе над проектом применялись следующие теоретические методы:

-изучение и анализ источников информации по комбинаторике и занимательной математике;

- моделирование приемов использования комбинаторики в задачах.

Понятие комбинаторика.

В обыденной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения, называются комбинаторными. Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой.

В Энциклопедическом словаре юного математика дано определение: «Комбинаторика — это раздел математики, в котором изучают, сколько комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов»[1]. Комбинаторика нужна для изучения раздела математики «Теория вероятностей», который будет являться обязательным при изучении школьного курса математики.

Способ рассуждений, которым пользуются при решении задачи, называют перебором возможных вариантов.

Раздел 2.

2.1. История развития комбинаторики

С задачами, получившими название комбинаторных, оказывается, люди сталкивались в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлеклись составлением магических квадратов, в которых заданные числа располагались так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же.

В Древней Греции подсчитывали число различных комбинаций длинных и коротких слов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата и т.д. Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.

Первым рассматривал комбинаторику как самостоятельную ветвь науки всемирно известный немецкий учёный Готфрид Вильгельм Лейбниц.

В 1666 году Лейбниц опубликовал «Рассуждения о комбинаторном искусстве». В своём сочинении Лейбниц, вводя специальные символы, термины , находит все k -сочетания из n элементов, выводит свойства сочетаний, строит таблицы сочетаний, после чего рассуждает о приложениях комбинаторики к логике, арифметике, к проблемам стихосложения и др. Мечтой Лейбница, оставшейся неосуществлённой, оставалось построение общей комбинаторной теории.

В XVIII веке к решению комбинаторных задач обращались выдающиеся математики. Замечательные достижения в области комбинаторики принадлежат Леонарду Эйлеру. Он рассматривал задачи о разбиении чисел, о циклических расстановках, о построении магических и латинских квадратов. В 1713 году было опубликовано сочинение Я. Бернулли, в котором с достаточной полнотой были изложены известные к тому времени комбинаторные факты. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т.д. Комбинаторные задачи физики, химии, биологии, экономики и других наук, которые не поддавались ранее решению из-за трудоемкости вычислений, стали успешно решаться на ЭВМ. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники. В частности, с помощью ЭВМ решена проблема четырех красок: доказано, что любую карту можно раскрасить в четыре цвета так, чтобы никакие две страны, имеющие общую границу, не были окрашены в один и тот же цвет.

Еще в 1844 году Дж. Сильвестр говорил: "Число, положение и комбинация - три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математические идеи".

2.2. Дерево возможных вариантов.

Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода - дерево возможных вариантов. Ветви дерева отображают различные события, которые могут иметь место. Корень дерева – состояние, в котором возникает необходимость выбора.

Задача 1. Какие трехзначные числа можно составить из цифр 0, 2, 4?

Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.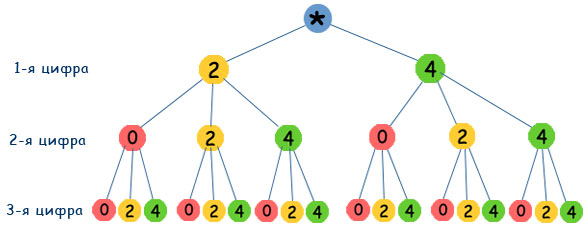

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.

Задача 2. Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап - на байдарках, велосипедах или пешком. И третий этап пути - пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?

Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе - А, на байдарках - Б, велосипедах - В, пешком - Х, на канатной дороге - К.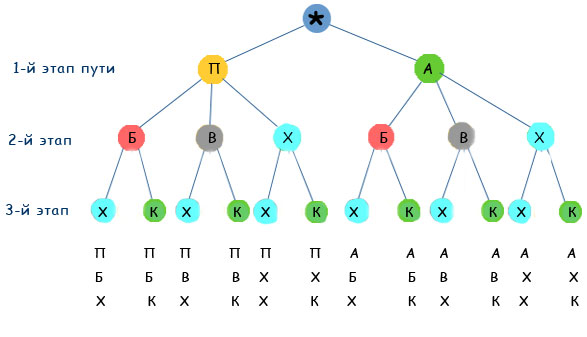

Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.

Задача 3. Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.

Решение. Построим дерево возможных вариантов, обозначив М - математика, Р - русский язык, И - история, А - английский язык, Ф - физкультура.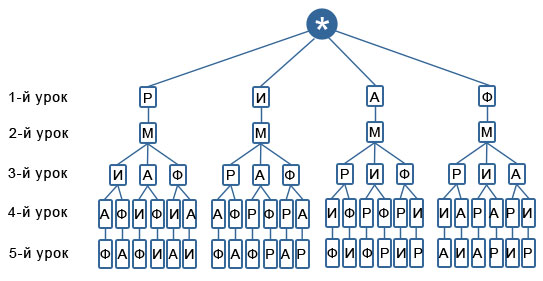

Ответ: Всего 24 возможных варианта.

Задача 4.

Саша ходит в школу в брюках или джинсах, к ним надевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки.

а) Сколько дней Саша сможет выглядеть по-новому?

б) Сколько дней при этом он будет ходить в кроссовках?

в) Сколько дней он будет ходить в рубашке в клетку и джинсах?

Решение. Построим дерево возможных вариантов, обозначив Б - брюки, Д - джинсы, С - серая рубашка, Г - голубая рубашка, З - зеленая рубашка, Р - рубашка в клетку, Т - туфли, К - кроссовки.

Ответ: а) 16 дней; б) 8 дней; в) 2 дня.

2.3. Перестановки.

Простейшими комбинациями, которые можно составить из элементов конечного множества являются перестановки.

Два элемента a и b могут быть выписаны в строчку всего двумя способами: ab и ba. Для трёх элементов, существует 6 вариантов. Посчитаем и число перестановок для 4 элементов:

1234, 1243, 1324, 1342, 1423, 1432,

2134, 2143, 2314, 2341, 2413, 2431,

3124, 3142, 3214, 3241, 3412, 3421,

4123, 4132, 4213, 4231, 4312, 4321.

Всего 24 перестановки, расположенные в 4 столбца по 6 перестановок в каждом.

Для числа перестановок n элементов есть обозначение: n! (читаем: «эн факториал»).

Факториал равен произведению всех натуральных чисел от n до 1.

Например, 4! = 1 · 2 · 3 · 4= 24. Здорово! Одна строчка, а перебирая все возможные случаи выше, сколько записи всех перестановок. А если бы было не 4 элемента, а 8? Значит, и не надо было выписывать все возможные перестановки. Неужели так просто. Вот задачи, которые я смог решить.

Задача 1. В семье – 6 человек, и за столом в кухне стоят 6 стульев. Семья решила каждый вечер, ужиная, рассаживаться на эти стулья по-новому. Сколько дней члены семьи смогут осуществлять задуманное?

Решение. Ответ оказывается неожиданно большим: получается почти два года! Объясню его.

Для удобства рассуждений , будем считать, что семья (бабушка, дедушка, мама, папа, дочь, сын) будет рассаживаться на стулья поочередно. Меня интересует, сколько всего существует различных способов их размещения на стульях. Предположим, что первой усаживается бабушка. У нее имеется 6 вариантов выбора стула. Вторым садится дедушка и независимо выбирает стул из 5оставшихся. Мама делает свой выбор третьей, и выбор у нее будет из 4 стульев. У папы будет уже три варианта, у дочки – 2, ну а сын сядет на единственный незанятый стул. По правилу умножения получаем, что имеется 720 различных способов размещения. Таким образом, в «игру с рассаживаниями» семья может играть 720 дней, т.е. почти два года. [3] Теперь стало понятно, что в обеих задачах речь шла о пяти перестановках.

Задача 2. Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?

Решение: Составим сначала все пары, в которые входит Антонов (для краткости будем писать первые буквы фамилий).

Получим три пары: АГ, АС, АФ.

Выпишем теперь пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС, ГФ.

Далее составим пары, в которые входит Сергеев, но не входят Антонов и Григорьев. Такая пара только одна: СФ.

Других вариантов составления пар нет, так как все пары, в которые входит Федоров, уже составлены.

Итак, мы получили 6 пар:

АГ, АС, АФ

ГС, ГФ

СФ,

т.е. 3•2•1=6. значит,

существует всего шесть вариантов выбора тренером пары теннисистов из группы.

2.4. Размещение

Следующее важное понятие комбинаторики — размещение.

Размещением называется расположение «предметов» (объектов) на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны.

Задача 1. В кафе предлагают два первых блюда: борщ, рассольник – и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель.

Решение:

Борщ

Рассольник

гуляш

котлеты

сосиски

пельмени

гуляш

котлеты

сосиски

пельмени

Ответ: 8 обедов.

Задача 2. В классе, в котором 25 учеников, нужно выбрать командира, его заместителя и помощника заместителя. Сколькими способами это можно сделать?

Решение:

1. 25 способами можно выбрать любого ученика в командиры.

2. Затем из 24 оставшихся — заместителя старосты.

3. После этого любой из 23 оставшихся может оказаться помощником заместителя.

Всего имеем: 25·24·23 = 13800

Ответ: 13800 способов.

Задача 3. В футбольной команде (11 человек) нужно выбрать капитана и вратаря. Сколькими способами это можно сделать?

Решение:

1. Капитаном может стать любой из 11 футболистов.

2. После выбора капитана на роль вратаря могут претендовать 10 оставшихся человек.

Таким образом, есть 11 · 10 = 110 разных вариантов выбора.

Ответ: 110 способов.

Задача 4. Сколько семизначных чисел не содержат цифры 2?

Решение:

Всего цифр 10. Первую цифру не может быть нулем и двойкой, значит её можно выбрать 8 способами. Каждую следующую цифру можно выбрать 9 способами.

8 · 9 · 9 · 9 · 9 · 9 · 9 = 4 251 528.

Ответ. 4 251 528 семизначных чисел.

Вот это количество. А если бы не знать этот способ решения, перебрать все возможные случаи, кажется, невозможно. Это долго и опасно ошибиться.

Задача 5. Сколькими способами можно составить расписание на день из 5 различных уроков, если изучается 14 предметов.

Решение:

В данном примере из 14 предметов нужно выбрать 5. Число способов составления расписания можно посчитать по формуле:

14 · 13 · 12 · 11 · 10 = 240240

Ответ: 240240 способов.

Задача 6. Сколько времени потребуется, чтобы открыть дверь с кодовым замком, если на один набор чисел из 3-х цифр уходит 3 секунды. (Причем порядок нажатия кнопок с числами неважен).

Решение: Первую цифру кода можно выбрать одной из 10 - всего 10 вариантов. Вторую цифру можно выбрать любой из 9 оставшихся. Значит, всего 10*9*8 = 720 комбинаций. Решение было бы верно, если бы не замечание в задаче: Причем порядок нажатия кнопок с числами неважен. Это означает, что композиция 123, 321, 213, и т.п. (всего их 6) одинаковые.

Поэтому надо брать не размещение, а сочетания. Для сочетаний – результат нужно разделить на 6, т.е. на число перестановок из трёх элементов, равных 3!.

720 : 6=120 комбинаций, 120 · 3 = 360 секунд = 6 минут и код будет разгадан.

Ответ: 6 минут.

3. Комбинаторика в различных областях жизнедеятельности человека.

Области применения комбинаторики:

• учебные заведения (составление расписаний)

• сфера общественного питания (составление меню)

• лингвистика (рассмотрение вариантов комбинаций букв)

• география (раскраска карт)

• спортивные соревнования (расчёт количества игр между участниками)

• производство (распределение нескольких видов работ между рабочими)

• агротехника (размещение посевов на нескольких полях)

• азартные игры (подсчёт частоты выигрышей)

• химия (анализ возможных связей между химическими элементами)

• экономика (анализ вариантов купли-продажи акций)

• криптография (разработка методов шифрования)

• доставка почты (рассмотрение вариантов пересылки)

• биология (расшифровка кода ДНК)

• военное дело (расположение подразделений)

• астрология (анализ расположения планет и созвездий)

3.1 Комбинаторика в литературе.

В басне Ивана Андреевича Крылова «Квартет»: «проказница Мартышка, Осёл, Козёл да косолапый Мишка» устроили любопытный эксперимент, они исследовали влияние взаимного расположения музыкантов на качество исполнения.

Проказница-Мартышка, Осёл, Козёл, да косолапый Мишка

Затеяли сыграть Квартет.

Достали нот, баса, альта, две скрипки

И сели на лужок под липки — пленять своим искусством свет.

Ударили в смычки, дерут, а толку нет.

«Стой, братцы, стой! — кричит Мартышка. — Погодите!

Как музыке идти? Ведь вы не так сидите.

Ты с басом, Мишенька, садись против альта,

Я, прима, сяду против вторы;

Тогда пойдёт уж музыка не та: у нас запляшут лес и горы!»

Расселись, начали Квартет;

Он всё-таки на лад нейдёт.

«Постойте ж, я сыскал секрет, —

Кричит Осёл: — мы, верно, уж поладим, коль рядом сядем».

Послушались Осла: уселись чинно в ряд;

А всё-таки Квартет нейдёт на лад.

Вот пуще прежнего пошли у них разборы

И споры, кому и как сидеть.

Случилось Соловью на шум их прилететь.

Тут с просьбой все к нему, чтоб их решить сомненье:

«Пожалуй, — говорят: — возьми на час терпенье,

Чтобы Квартет в порядок наш привесть:

И ноты есть у нас, и инструменты есть;

Скажи лишь, как нам сесть!» —

«Чтоб музыкантом быть, так надобно уменье

И уши ваших, понежней, —

Им отвечает Соловей: —

А вы, друзья, как ни садитесь,

Всё в музыканты не годитесь».

Мартышка, Осёл, Козёл и Мишка пересаживались, считая, что от этого зависит звучание музыки. И если бы не вмешался Соловей, участники квартета, наверное, перепробовали бы все возможные варианты.

Так сколько же существует способов, чтобы рассадить, например в один ряд, четырех музыкантов?

Число перестановок можно посчитать по формуле: 4  3  2 1 = 24 способа.

Ответ: 24 способа.

3.2 Комбинаторика на шахматной доске и в играх.

Шахматы не только популярная игра, но и источник множества интересных комбинаторных задач. Не случайно шахматные термины можно встретить в литературе по комбинаторике. Рассмотрим примеры задач на шахматной доске.

Задача 1: Обойти конем все поля доски, посетив каждое из них по одному разу.

Этой задачей занимались многие математики XVIII и XIX вв., в том числе и Л. Эйлер. Хотя задача была известна и до Эйлера, лишь он впервые обратил внимание на ее математическую сущность. Доказано, что таких маршрутов не более 30 млн. Задачи о маршрутах составлены и для других фигур.

Задача 2: Сколькими способами можно расставить на доске восемь ферзей так, чтобы они не угрожали друг другу, т. е. никакие два из них не стояли бы на одной линии ( вертикали, горизонтали, диагонали).

Доказано, что существует 92 требуемых расстановки. Подобные задачи ставятся для всех шахматных фигур. Исследование конкретных позиций или их классов в игре применяется для достижения определенных результатов, например матовой позиции за определенное число ходов. Так как борьба за уменьшение времени на «обдумывание» хода всей программой является принципиальным фактором, то математики затрачивают массу усилий на создание входящих в нее приложений (задач, решаемых при поиске нужного хода), работающих наиболее быстро, а также требующих по минимуму оперативной памяти. Это направление породило множество изящных логико-вычислительных проблем. Некоторые из них и по сей день предлагаются на различных математических и программистских олимпиадах, а также для развлечения на досуге.

Выдающиеся шахматисты Клод Шеннон и Михаил Ботвинник внесли огромный вклад в создание математической модели шахматной игры и способствовали прогрессу в интеллектуализации программ для нее.

Компьютерные шахматы — едва ли не самый убедительный пример за полвека развития информационных технологий, когда именно в интеллектуальной деятельности автомат успешно соперничает с человеком.

3.3 Комбинаторика и кубик Рубика.

Необыкновенно популярной головоломкой стал кубик Рубика, изобретенный в 1975 году преподавателем архитектуры из Будапешта Эрне Рубиком для развития пространственного воображения у студентов.

Кубик Рубика – это куб, как бы разрезанный на 27 одинаковых кубиков. В исходном положении каждая грань куба окрашена в один из 6 цветов. Остроумный механизм позволяет поворачивать любой слой из 9 кубиков, примыкающий к одной грани куба, вокруг ее центра. При этом цвета граней смешиваются. Задача состоит в том, чтобы вернуть разноцветные грани кубика в исходное положение. Теоретически из любого состояния кубика можно вернуться в исходное, не более чем за 23 хода. Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды.

Кубик Рубика служит не только развлечением, но и прекрасным наглядным пособием по комбинаторике.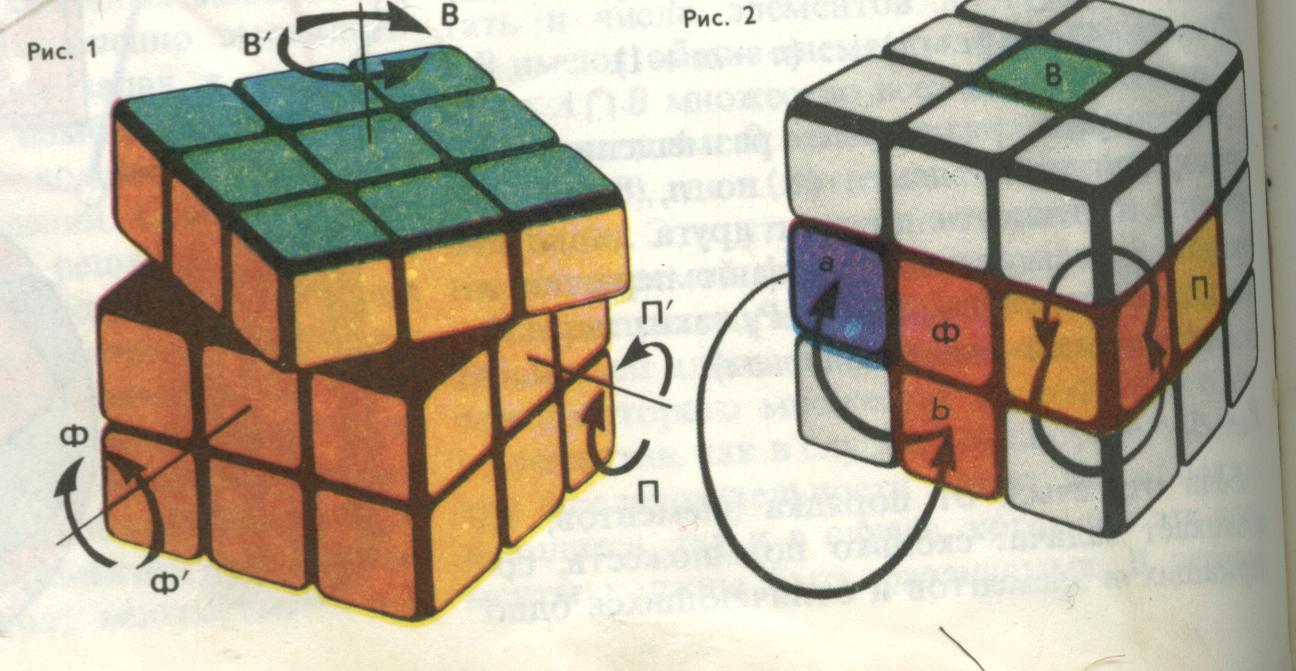

3.4 Старинные задачи

Задача: «Волк, козел и капуста»

Крестьянину нужно перевезти через реку волка, козла и капусту. Лодка так мала, что в ней кроме крестьянина может поместиться только или волк, или козел, или капуста. Но если оставить волка с козлом, он его съест, а если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину?

Для решения требуется путем взаимной перестановки элементов расположить их в соответствии с условием задачи в определенном порядке. В случае с крестьянином переправу следует начать с перевозки козла. Затем крестьянин возвращается и берет волка, которого перевозит на другой берег и оставляет там, а козла возвращает назад на предыдущий берег. Оттуда забирает капусту и перевозит ее к волку. А затем возвращается и забирает козла.

Задача-игра: «Крестики-нолики»

Самая известная древняя игра. В квадрате, разделенном на девять клеток, игроки по очереди ставят в свободную клетку свой знак: крестик или нолик, стараясь выстроить три крестика или три нолика подряд. Тот, кто первым сделает это, тот и выигрывает.

Если не делать ошибок, то игра оканчивается в ничью. Выиграть можно только в том случае, если противник ошибется. Самый правильный ход –

занять угловую клетку. И если партнер не ответит на это своим знаком в центре, то он проиграл.

Задача-игра: «Ним» Пусть имеется одна или несколько групп предметов. Играющие берут по очереди предметы из групп по правилам, которые заранее устанавливают: какое количество предметов разрешается брать за один раз и из скольких групп. Существует множество вариантов игры, и для большинства известна наилучшая стратегия, ведущая к выигрышу.

Заключение

В ходе проекта мною рассматривается история возникновения комбинаторики как науки, начиная с Древнего Китая и Древней Греции и заканчивая современным периодом ее развития. В работе приводятся сведения о великих математиках, которые стояли у истоков теории комбинаторных задач таких, как П. Ферма, Галилео Галилей, Я. Бернулли, Паскаль, Лейбниц, Л. Эйлер и многие другие.

Таким образом, изложенные сведения, доказывают, что комбинаторные задачи сопровождают человечество на протяжении всей истории, переплетаясь с искусством и наукой, что математике присущ элемент игры, которая тренирует интеллект и развивает самые различные способности, особенно творческие.

В рамках проекта полученная информация была изучена и применена при решении задач на перестановки, размещения, и были сделаны выводы, что несомненно, знание правил решения комбинаторных задач дает шанс намного быстрее прийти к положительному результату в логических рассуждениях.

В ближайшем будущем я научусь решать более сложные задачи комбинаторики, а знания по этой теме будут востребованы при решении задач олимпиадного типа и помогут мне в будущем при подготовке к итоговой аттестации по математике.

Вывод: Комбинаторика повсюду. Комбинаторика везде. Комбинаторика вокруг нас. Думаю, что цели я добился, так как после написания работы расширил и углубил свои знания по комбинаторике и научился решать задачи из этого раздела.

Литература:

1.Энциклопедический словарь юного математика - /составитель Савинов А.П..- М.: Педагогика » -1985г.-352стр с ил.

2.Виленкин Н.Я. Комбинаторика.: Изд. « Наука»,1969г.

3.Деплан И. Я ., Виленкин Н.Я. За страницами учебника математики.- Пособие для учащихся 5-6кл средних школ. М.:Просвещение,1989-287стр. с иллюстрациями.

4.Г. Я. Гик «Занимательные математические игры». - М.:Знание,1982г.

5.Математическая энциклопедия /Виноградов И.М..-М.:Советская энциклопедия. Том 3.,1984г

6.Богомолов Н.В. Практические занятия по математике: Учеб. Пособие для техникумов. – 2-е изд., перераб.-М.: Высш. Школа, 1983.-399 с., ил.

7.Энциклопедия для детей. Т.11. Математика/Глав. Ред. М.Д. Аксенова.- М.: Аванта+, 2002.- 688с.: ил.

8/

Раздел 5.

Приложение

Задача. У меня есть любимый костюм, в котором я хожу в школу. Я надеваю к нему белую, голубую, розовую или красную блузку. Кроме того у

Летом на каникулах наша семья планирует поездку в отпуск в г. Тюмень.

Сколько существует вариантов маршрутов из г. Белоярский до г. Тюмени

и какой из них выгодней по времени и стоимости?

infourok.ru

История комбинаторики

Содержание

• 1 Древний период
• 2 Средневековье
• 3 Новое время
• 4 Современное развитие
• 5 См. также
• 6 Примечания
• 7 Литература

Древний период

Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.

Классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.).. Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона. Во II веке до н. э. индийцы знали, что сумма всех биномиальных коэффициентов степени n равна 2 n {\displaystyle 2^{n}} .

Античные греки также рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов, если оно и существовало, до нас не дошло. Хрисипп (III век до н. э.) и Гиппарх (II век до н. э.) подсчитывали, сколько следствий можно получить из 10 аксиом; методика подсчёта нам неизвестна, но у Хрисиппа получилось более миллиона, а у Гиппарха — более 100000. Аристотель при изложении своей логики безошибочно перечислил все возможные типы трёхчленных силлогизмов. Аристоксен рассмотрел различные чередования длинных и коротких слогов в стихотворных размерах. Какие-то комбинаторные правила пифагорейцы, вероятно, использовали при построении своей теории чисел и нумерологии (совершенные числа, фигурные числа, пифагоровы тройки и др.).

Средневековье

В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.

В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра подсчитывал число размещений с перестановками в огласовках имени Бога и обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.

Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.

Новое время

Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

• задача о ходе коня;
• задача о семи мостах, с которой началась теория графов;
• построение греко-латинских квадратов;
• обобщённые перестановки.

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Современное развитие

В начале XX века начала развиваться комбинаторная геометрия: были доказаны теоремы Минковского — Радона, Радона, Хелли, Юнга, Бляшке, а также строго доказана изопериметрическая теорема. На стыке топологии, анализа и комбинаторики были доказаны теоремы Борсука — Улама и Люстерника — Шнирельмана. Во второй четверти XX века были поставлены проблема Борсука и проблема Нелсона — Эрдёша — Хадвигера. В 1940-х годах оформилась теория Рамсея. Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.

См. также

• Теория графов
• Теория игр

Примечания

1. ↑ Виленкин Н. Я., 1975, с. 7.
2. ↑ 1 2 Amulya Kumar Bag. Binomial theorem in ancient India. Indian J. History Sci., 1:68-74, 1966.
3. ↑ 1 2 Виленкин Н. Я., 1975, с. 9.
4. ↑ Краткий комментарий к Исход, 3:13.
5. ↑ Виленкин Н. Я., 1975, с. 19.
6. ↑ O'Connor, John; Edmund Robertson. Abraham de Moivre. The MacTutor History of Mathematics archive (06 2004). Проверено 31 мая 2010. Архивировано из первоисточника 27 апреля 2012.

Литература

• Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — 208 с.
• История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Рыбников К. А. Комбинаторный анализ. Очерки истории. — М.: Изд. мехмата МГУ, 1996. — 124 с.
• Рыбников К. А. История математики в двух томах. — М.: Издательство МГУ, 1960-1963.

История комбинаторики Информация о

История комбинаторики Информация Видео

История комбинаторики что, История комбинаторики кто, История комбинаторики объяснение

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com

Смотрите также

• 
  Древняя греция фивы
• Древняя греция игпзс
• 
  Самые древние рептилии
• Политика древней месопотамии
• 
  Легенды древнего казахстана
• 
  Историография древней греции
• 
  Древние профессии список
• 
  Древний замок рисунок
• 
  Древний герб смоленска
• 
  Рисунок древний замок
• 
  Градостроительство древнего египта